Astar算法
A*(Dijkstra with a Heuristic)
**1)Strategy: expand the node with cheapest f(n) = g(n) + h(n) **
Accumulated cost
• g(n): The current best estimates of the accumulated cost from the start state to node “n”
(从开始状态到节点“n”的累积成本的当前最佳估计)
Heuristic
• h(n): The estimated least cost from node n to goal state (i.e. goal cost)
(节点n到目标状态的估计最小成本(即目标成本))
The least estimated cost from start state to goal state passing through node“n” is f(n) = g(n) + h(n)
(从起始状态到目标状态通过节点n的最小估计代价为f(n) = g(n) + h(n))
2)A* Algorithm
• Maintain a priority queue to store all the nodes to be expanded
• The heuristic function h(n) for all nodes are pre-defined
• The priority queue is initialized with the start state XS
• Assign g(XS)=0, and g(n)=infinite for all other nodes in the graph
• Loop
*• If the queue is empty, return FALSE; break;*
*• Remove the node “n” with the lowest f(n)=g(n)+h(n) from the priority queue*
*• Mark node “n” as expanded*
*• If the node “n” is the goal state, return TRUE; break;*
*• For all unexpanded neighbors “m” of node “n”*
*• If g(m) = infinite*
*• g(m)= g(n) + Cnm*
*• Push node “m” into the queue*
*• If g(m) > g(n) + Cnm*
*• g(m)= g(n) + Cnm*
*• end*
• End Loop
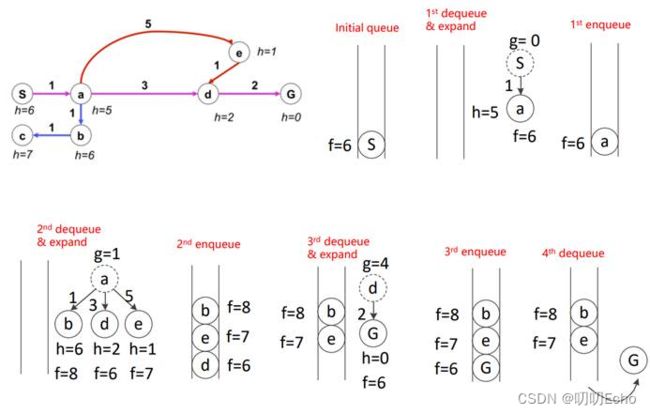
| 1 | 2 | |
|---|---|---|
| open list | f(s)=g(s)+h(s)=6 | f(a)=g(a)+h(a)=6 |
| close list | f(s)=6 |
| 3 | 4 | 5 |
|---|---|---|
| f(d)=g(d)+h(d)=6,f(e)=g(e)+h(e)=7,f(b)=g(b)+h(b)=8 | f(G)=g(G)+h(G)=6,f(e)=g(e)+h(e)=7,f(b)=g(b)+h(b)=8 | 取到终点,结束 |
| f(s)=6,f(a)=6 | f(s)=6,f(a)=6,f(d)=6 |
3)A* Optimality
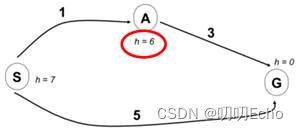
What went wrong?
• For node A: actual least cost to goal (i.e. goal cost) < estimated least cost to goal (i.e. heuristic)
(对于节点A:实际到目标的最小成本(即目标成本)<估计到目标的最小成本(即启发式))
• We need the estimate to be less than actual least cost to goal(i.e. goal cost) for all nodes!
(我们需要估计值小于实际的目标最低成本(即:目标成本)为所有节点!)
(我们需要估计值小于实际的目标最低成本(即:目标成本)为所有节点!)
4)Admissible Heuristics(可接受的启发)
• A Heuristic h is admissible (optimistic) if:
• h(n) <= h*(n) for all node “n”, where h*(n) is the true least cost to goal from node “n”
(设计的重点:h (n) <= h *(n)对于所有节点“n”,其中h *(n)是从节点“n”到目标的真正最小代价)
An admissible heuristic function has to be designed case by case.
• Euclidean Distance
• Manhattan Distance
Is Euclidean distance (L2 norm) admissible? Always
Is Manhattan distance (L1 norm) admissible? Depends
Is L∞ norm distance admissible? Always
Is 0 distance admissible? Always
2.2.3 Dijkstra’s vs A*
2.2.4 Sub-optimal Solution(次优解)
What if we intend to use an over-estimate heuristic?
用最优性换取速度
2.2.5 Greedy Best First Search vs. Weighted A* vs. A*
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AgBjh1A3-1679732853021)(路径规划.assets/clip_image032.jpg)]
Engineering Considerations
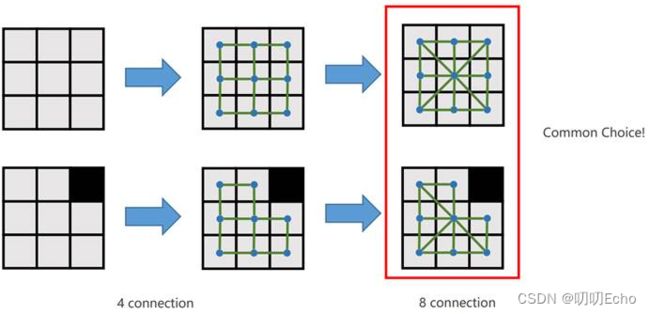
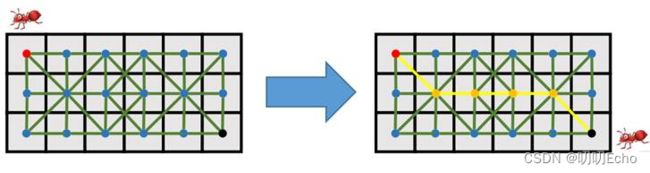
2.2.6 How to represent grids as graphs?(如何将网格表示为图形?)
Each cell is a node. Edges connect adjacent cells.(每个单元格是一个节点,边连接相邻的单元格。)
Grid- based Path Search: Implementation
• Create a dense graph.
• Link the occupancy status stored in the grid map.
• Neighbors discovered by grid index.
• Perform A* search.
Priority queue in C++
• std::priority_queue
• std::make_heap
• std::multimap
(推荐c++的库)
2.2.7 The Best Heuristic
1.They are useful, but none of them is the best choice, why?
Because none of them is tight.
Tight means who close they measure the true shortest distance.
(因为它们都不是紧密的。紧意味着靠近他们真正的最短距离。)
2.Why so many nodes expanded?
Because Euclidean distance is far from the truly theoretical optimal solution.
(因为欧几里德距离远不是真正的理论最优解。)
3.How to get the truly theoretical optimal solution?
Fortunately, the grid map is highly structural.(幸运的是,网格地图是高度结构化的。)
It has the closed-form solution!(它有封闭式的解决方案!)
解:(列方程)
dx=abs(node.x −goal.x)
dy=abs(node.y −goal.y)
h=(dx+dy)+(√2−2)∗min(dx,dy) (h*(最优的h)=h(真值)=Diagonal Heuristic)
(3D也可以延伸,也是有一定的方程解的)
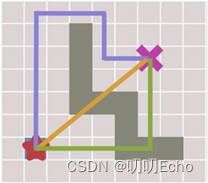
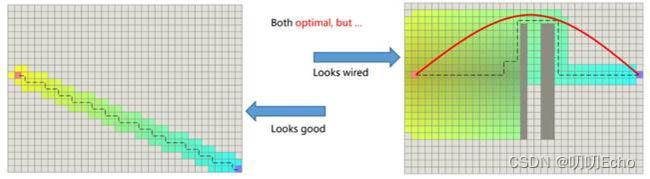
2.2.8 Tie Breaker(打破平衡)
原因:1.Many paths have the same f value.
2.No differences among them making them explored by A* equally.
Path具有对称性(长度一样,结果一样的不同路径),要对搜索的路径进行简化,打破平衡。
具体的解决办法:
1)修改Heuristic函数
思路:a)Manipulate the value breaks the tie.(打破f值的平衡)
b)Make same values differ.(让f值不同)
c)Interfere ℎ slightly.(轻微地改变f值)
步骤:
h(预估的启发式函数) Core idea of tie breaker: Prefer paths that are along the straight line from the starting point to the goal.结果:
Slightly breaks the admissibility of h, does it matter?(稍微打破了h的可行性,有关系吗?)
答:没有关系,在实际的运用中,肯定的会有很多的障碍物,这些障碍物的阻碍,肯定会使预估的h远远小于理想的h*。
Find a preference among same cost paths.(在相同中找到一个优先的路径)
• When nodes having same , compare their ℎ.
• Add deterministic random numbers to the heuristic or edge costs (A hash of the coordinates). 哈希表
• Prefer paths that are along the straight line from the starting point to the goal.
1 = . − . )
1 = (. − . )
2 = (. − . )
2 = (. − . )
= (1 × 2 − 2 × 1)
h = ℎ + × 0.001
• … Many customized ways
It’s the shortest path, but harm for trajectory generation (smoothing).
(这是最短的路径,但对轨迹生成(平滑)有害。)
还不利于后面轨迹优化,轨迹生成
Or a systematic approach: Jump Point Search (JPS)