从傅里叶变换到小波变换详细解释(含代码)

1、从傅里叶变换到小波变换

傅里叶变换能够将一个信号从时域转换为频域，在转换后的频谱中，频谱的峰值越大越尖，表示对应频率的信号就强度就越大。

傅里叶变换能够处理不随时间变化的平稳信号，即它能告诉我们信号包含哪些频段，但是不能告诉我们这个频段是在信号的哪个时间段出现的。而生活中更多的是随着时间变化而发生一定变化的非平稳信号，而对于这些信号，傅里叶变换就难以进行处理，因此演化出了可以处理非平稳信号的小波变换。

如上图所示，signal1和signal2两个信号都是由4个不同频率叠加得到的，只是叠加形式不一样；对于signal1，四个不同频率的信号直接进行叠加，因为信号不随时间变化而产生非平稳变化，因此傅里叶变换可以轻松得到结果；但是对于信号signal2，四个不同频率的信号以此在时间轴上展开，傅里叶变换就不能得出有效的结果了。

那么如何解决这个问题呢？短时傅里叶变换就出现了，想法很容易理解：如果将信号分割相同的n份，傅里叶变换找出特殊的信号在第几个部分出现，那么我们就知道对应的这个特殊信号频段出现在原始信号的哪一段了。

但是这种方法也有问题，因为把窗口的大小做得越小，就越能知道信号中某个频率出现在哪里，但是自身的频率值获得的就越少。窗口的大小越大，我们对频率值的了解就越多，而对时间的了解就越少。可以说是短时傅里叶变换不能够兼顾频域信息与时域信息。

因此短时傅里叶变换并不能很好解决这个问题，也可以说是引入了频域信息与时域信息不兼容的问题。那么如何解决这个问题呢？这就引出了小波变换，它可以很好地处理这种动态频谱信息。小波变换不仅能够告诉我们在信号中有哪些频率出现，而且能够告诉我们在信号的什么时候出现。小波变换的实现是通过不同的伸缩变换完成的。它能够根据不同尺度的信号调节成不同大小的窗口，既能有效分析大尺度信号，也能有效分析小尺度信号，即既兼顾了时间信号，又兼顾了频率信号。

下面用程序来说明这个问题：

import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft

t_n = 1
N = 200

xa = np.linspace(0, t_n, num=N)
xb = np.linspace(0, t_n / 4, num=N // 4)

def get_fft_values(y_values, N):
    xf = np.arange(len(y_values)) 
    f_values = xf[range(int(N / 2))]
    # f_values = np.linspace(0.0, 1.0,N // 2)
    fft_values_ = fft(y_values)
    fft_values = 2.0 / N * np.abs(fft_values_[0:N // 2])
    return f_values, fft_values


frequencies = [4,30, 60, 90]  
y1a, y1b = np.sin(2 * np.pi * frequencies[0] * xa), np.sin(2 * np.pi * frequencies[0] * xb)
y2a, y2b = np.sin(2 * np.pi * frequencies[1] * xa), np.sin(2 * np.pi * frequencies[1] * xb)
y3a, y3b = np.sin(2 * np.pi * frequencies[2] * xa), np.sin(2 * np.pi * frequencies[2] * xb)
y4a, y4b = np.sin(2 * np.pi * frequencies[3] * xa), np.sin(2 * np.pi * frequencies[3] * xb)

composite_signal1 = y1a + y2a + y3a + y4a  
composite_signal2 = np.concatenate([y1b, y2b, y3b, y4b])  

f_values1, fft_values1 = get_fft_values(composite_signal1, N)
f_values2, fft_values2 = get_fft_values(composite_signal2, N)

fig, axarr = plt.subplots(nrows=2, ncols=2, figsize=(8, 6))
axarr[0, 0].plot(xa, composite_signal1)
axarr[1, 0].plot(xa, composite_signal2)
axarr[0, 1].plot(f_values1, fft_values1)
axarr[1, 1].plot(f_values2, fft_values2)

plt.tight_layout()
plt.show()

![在这里插入图片描述](https://img-blog.csdnimg.cn/6bcdccb1615041e4a0c91f988f5fea2e.png
上图中我们能看到左上角的信号中包含4种不同的频率(4，30，60，90)赫兹 ，所有频率在这段时间内全部出现，右上角是这个信号的频谱。
在下边的两个图中，我们同样能看到这4种频率，但是第一种出现在1/4时间上，之后的频率依次出现。并且我们能在右下面看到这个信号的频谱图。

值得注意的是两个频谱图都包含了4个峰值，但是他们都不能明确表示出在信号的哪个时间段出现的。这就使得傅里叶变换不能区分这个两个信号。

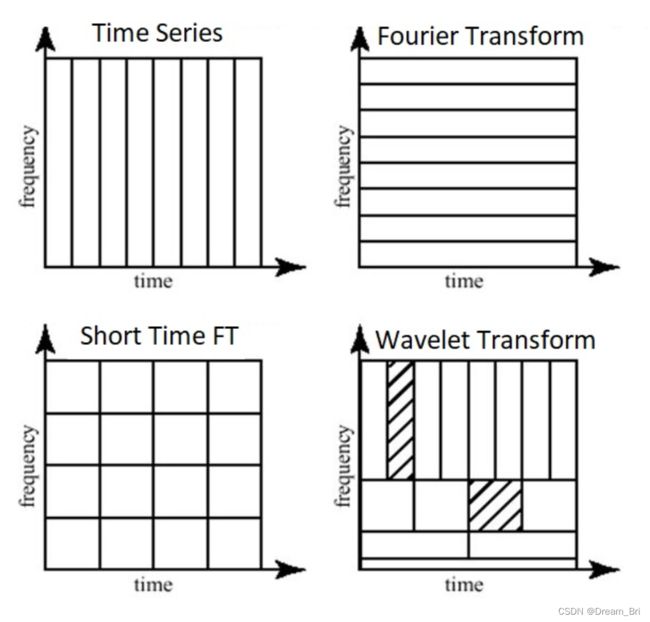
下面，我们用一张图来说明小波变换与短时傅里叶变换的差异。
我们可以把竖状长方形当作时间信息，把横状长方形当作频域信息，短时傅里叶变换是通过统一大小窗口进行变换，那么它在时间域和频率域都只能有中等的分辨率。而右下角的小波变换却可以根据信号需要变换长方形的长宽胖瘦，因而在时间域和频率域上都能根据需要得到较好的分辨效果。

小波变换在时频域变换特征为：
对于小频率值，频域分辨率高，时域分辨率低；
对于大频率值，频域分辨率低，时域分辨率高。

2、图像化感受小波变换中的小波

傅里叶变换是通过一系列频率不同的正弦波来拟合信号的。而小波变换是使用一系列称为小波的函数(每个函数具有不同的尺度)拟合信号的。这里的小可以认为是时间特征上的小。

由上图我们可以看出，正弦波是在时间上无限延长且保持周期变化，而小波则是在某一个时间点或时间段上有信号幅值，是局域波。因此小波不仅包含了频率的信息，同时也包含了时间的信息。

小波是在时间域的函数，那么我们叠加不同时间段的小波，让小波信号从研究信号的开始的时间点慢慢向结束时间点上移动，即进行卷积操作。在对原始小波操作完后，我们可以改变小波尺寸，然后继续上面的操作。进而就得到了研究信号的整个时域和频域信息了。

3、小波变换族中的分类

傅里叶变换和小波变换的另一个不同的地方是小波中有很多不同的族。小波族之间是不同的，因为每个小波族在小波的紧凑性和平滑性方面都做出了不同的权衡。这意味着我们需要根据对应的特征选择一个特定的小波族。

通过pywt函数，可以看到小波变换中有多少个族类。
代码及其结果显示如下：

import pywt
print(pywt.families(short=False))

# 显示的结果
['Haar', 'Daubechies', 'Symlets', 'Coiflets', 'Biorthogonal', 'Reverse biorthogonal', 
'Discrete Meyer (FIR Approximation)', 'Gaussian', 'Mexican hat wavelet', 'Morlet wavelet', 
'Complex Gaussian wavelets', 'Shannon wavelets', 'Frequency B-Spline wavelets', 'Complex Morlet wavelets']

小波之所以有很多的族类，对应着不同的形状、光滑度和紧密型，应用于不同的场景和状况，是因为小波族类的产生只需要满足两个数学条件：归一化约束和正交化约束。即小波必须有：1、有限的能量；2、零均值。

有限能量意味着它在时间和频率上是局域的，是可积的。零均值条件意味着小波在时域中均值为零，在时域中频率为零时均值为零。这对于保证小波变换的可积性和计算小波变换的逆是必要的。

在此，我们可以查看不同小波族的图像。下面图像中第一行包含四个离散小波，第二行包含四个连续小波。

小波族图像显示代码如下：

import pywt
from matplotlib import pyplot as plt

#print(pywt.families(short=False))
discrete_wavelets = ['db5', 'sym5', 'coif5', 'bior2.4']
continuous_wavelets = ['mexh', 'morl', 'cgau5', 'gaus5']

list_list_wavelets = [discrete_wavelets, continuous_wavelets]
list_funcs = [pywt.Wavelet, pywt.ContinuousWavelet]

fig, axarr = plt.subplots(nrows=2, ncols=4, figsize=(16,8))
for ii, list_wavelets in enumerate(list_list_wavelets):
    func = list_funcs[ii]
    row_no = ii
    for col_no, waveletname in enumerate(list_wavelets):
        wavelet = func(waveletname)
        family_name = wavelet.family_name
        biorthogonal = wavelet.biorthogonal
        orthogonal = wavelet.orthogonal
        symmetry = wavelet.symmetry
        if ii == 0:
            _ = wavelet.wavefun()
            wavelet_function = _[0]
            x_values = _[-1]
        else:
            wavelet_function, x_values = wavelet.wavefun()
        if col_no == 0 and ii == 0:
            axarr[row_no, col_no].set_ylabel("Discrete Wavelets", fontsize=16)
        if col_no == 0 and ii == 1:
            axarr[row_no, col_no].set_ylabel("Continuous Wavelets", fontsize=16)
        axarr[row_no, col_no].set_title("{}".format(family_name), fontsize=16)
        axarr[row_no, col_no].plot(x_values, wavelet_function)
        axarr[row_no, col_no].set_yticks([])
        axarr[row_no, col_no].set_yticklabels([])
plt.tight_layout()
plt.show()

4、小波族子类的分类

在每个小波族中，可以有许多不同的小波子类别属于这个族。可以通过系数的数量和分解的级别来区分小波的不同子类别。

下面我们以一个称为“Daubechies”族为例来研究查看其子类。

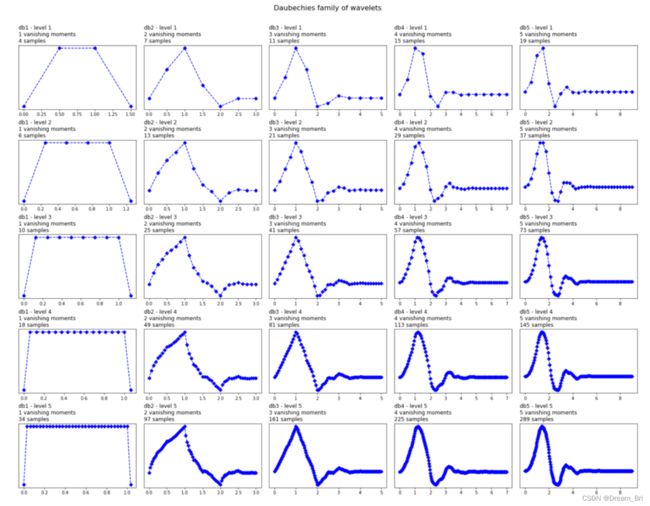
上图是多贝西小波族关于阶数的分类情况，从第一列到第五列，分别对应着db1到db5，当然在此我们用的Daubechies小波可以高达20阶，在此用5阶来进行研究和说明。

所用的阶数表示消失力矩的个数，因此db3有3个消失力矩，db5有5个消失力矩。消失力矩的个数与小波的逼近阶数和平滑度有关。如果一个小波有p个消失矩，那么它就可以近似为p - 1次多项式。

在选择小波时，我们还可以指出分解的级别。默认情况下，PyWavelets为输入信号选择可能的最大分解级别。分解的最大级别取决于输入信号长度和小波的长度。(用pywt.dwt_max_level()来查看)

根据上图可以看出，随着消失力矩阶数的增加，小波的多项式阶数也增加，小波变得更加平滑。

对应的代码显示如下：

import pywt
from matplotlib import pyplot as plt

db_wavelets = pywt.wavelist('db')[:5]
print(db_wavelets)
# ['db1', 'db2', 'db3', 'db4', 'db5']

fig, axarr = plt.subplots(ncols=5, nrows=5, figsize=(20,16))
fig.suptitle('Daubechies family of wavelets', fontsize=16)
for col_no, waveletname in enumerate(db_wavelets):
    wavelet = pywt.Wavelet(waveletname)
    no_moments = wavelet.vanishing_moments_psi
    family_name = wavelet.family_name
    for row_no, level in enumerate(range(1,6)):
        wavelet_function, scaling_function, x_values = wavelet.wavefun(level = level)
        axarr[row_no, col_no].set_title("{} - level {}\n{} vanishing moments\n{} samples".format(
            waveletname, level, no_moments, len(x_values)), loc='left')
        axarr[row_no, col_no].plot(x_values, wavelet_function, 'bD--')
        axarr[row_no, col_no].set_yticks([])
        axarr[row_no, col_no].set_yticklabels([])
plt.tight_layout()
plt.subplots_adjust(top=0.9)
plt.show()

5、连续小波变换与离散小波变换

小波变换有两种不同的变换形式：连续小波变换和离散小波变换。

数学上，连续小波变换的表达式为:

其中Ψ(t)为连续母波，a是尺度因子，b为平移因子。尺度因子和平移因子的值是连续的，这意味着可能有无限多的小波。

离散小波变换和连续小波变换主要的区别是：离散小波变换对尺度和平移因子使用离散值。缩放因子a以2的幂增加(a=1,2,4…… )，平移因子b 整数值(b=1,2,3)增加。

6、离散小波变换–DWT是一组滤波器

在实际应用中，离散小波变换总是被当作滤波器使用。这意味着它被实现为高通滤波器和低通滤波器的级联。这是因为滤波器组是一种非常有效的方法，将一个信号分解成几个子频带。

举个例子，假设我们有一个频率高达1000赫兹的信号。在第一个阶段，我们把信号分成低频部分和高频部分，即0- 500hz和500- 1000hz。在第二阶段，我们取低频部分，再次将其分为两部分:0-250赫兹和250-500赫兹。在第三阶段，我们将0-250赫兹的部分分为0-125赫兹的部分和125-250赫兹的部分。这种情况会一直持续下去，直到我们达到了所需的精化水平，或者直到我们的样本耗尽为止。

频率划分模式如下图所示：

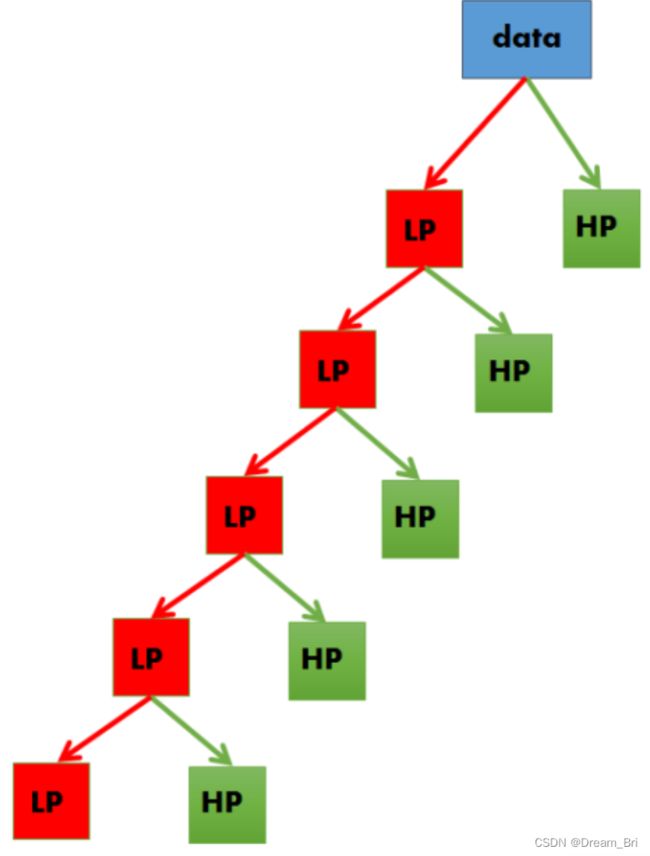
将一组信号均分为高频信号和低频信号后，如果进一步再划分，则将其低频信号的频率一分为二，再度产生一组新的高频信号和低频信号。上图所示是五阶小波划分。

下面，我们用程序的形式来对一组波形进行频率的划分。

import pywt
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 1, num=2048)
chirp_signal = np.sin(250 * np.pi * x ** 2)

fig, ax = plt.subplots(figsize=(6, 1))
ax.set_title("Original Chirp Signal: ")
ax.plot(chirp_signal)
plt.show()

data = chirp_signal
waveletname = 'sym5'

fig , axarr = plt.subplots(nrows=5, ncols=2, figsize=(6, 6))
for ii in range(5):
    (data, coeff_d) = pywt.dwt(data, waveletname)
    axarr[ii, 0].plot(data, 'r')
    axarr[ii, 1].plot(coeff_d, 'g')
    axarr[ii, 0].set_ylabel("Level {}".format(ii + 1), fontsize=14, rotation=90)
    axarr[ii, 0].set_yticklabels([])
    if ii == 0:
        axarr[ii, 0].set_title("Approximation coefficients", fontsize=14)
        axarr[ii, 1].set_title("Detail coefficients", fontsize=14)
    axarr[ii, 1].set_yticklabels([])
plt.tight_layout()
plt.show()

程序运行后的结果显示为：

原始chirp_signal信号显示：

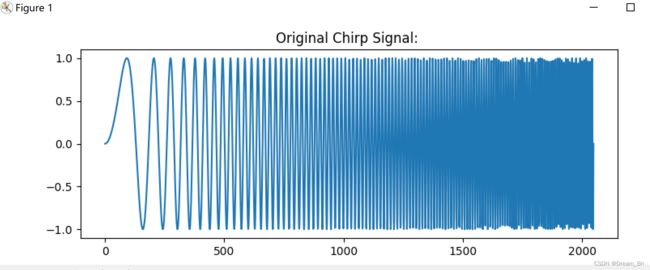
下图是chirp_signal信号进行sym5小波处理后(1 - 5级)的近似系数和细节系数显示，从1阶到5阶。左侧一列是小波近似系数，右侧是小波细节系数。

在小波中，离散小波变换(DWT)应用函数pywt.dwt()；
DWT返回两组系数：近似系数和细节系数；
近似系数表示小波变换的低通滤波器(平均滤波器)的输出；
细节系数表示小波变换的高通滤波器(差分滤波器)的输出；
通过对上一级小波变换的近似系数进行小波变换，得到下一级小波变换；
每下一层，原始信号的采样率也下降2倍。

7、连续小波变换实现状态空间的可视化

为了更好理解小波变换尺度图，让我们将它与原始的时间序列数据及其傅里叶变换一起可视化。

下面程序所用的数据来自一段ppg信号，读者可以自己选取一段任意的信号作为dataset输入即可。

import matplotlib.pyplot as plt
import numpy as np
import pywt
from scipy.fftpack import fft
import os
from scipy import signal


def plot_wavelet(time, signal, scales,
                 waveletname='cmor',
                 cmap=plt.cm.seismic,
                 title='Wavelet Transform (Power Spectrum) of signal',
                 ylabel='Period (years)',
                 xlabel='Time'):
    dt = time[1] - time[0]
    [coefficients, frequencies] = pywt.cwt(signal, scales, waveletname, dt)
    power = (abs(coefficients)) ** 2
    period = 1. / frequencies
    levels = [0.0625, 0.125, 0.25, 0.5, 1, 2, 4, 8]
    contourlevels = np.log2(levels)

    fig, ax = plt.subplots(figsize=(15, 10))
    im = ax.contourf(time, np.log2(period), np.log2(power), contourlevels, extend='both', cmap=cmap)

    ax.set_title(title, fontsize=20)
    ax.set_ylabel(ylabel, fontsize=18)
    ax.set_xlabel(xlabel, fontsize=18)

    yticks = 2 ** np.arange(np.ceil(np.log2(period.min())), np.ceil(np.log2(period.max())))
    ax.set_yticks(np.log2(yticks))
    ax.set_yticklabels(yticks)
    ax.invert_yaxis()
    ylim = ax.get_ylim()
    ax.set_ylim(ylim[0], -1)

    cbar_ax = fig.add_axes([0.95, 0.5, 0.03, 0.25])
    fig.colorbar(im, cax=cbar_ax, orientation="vertical")
    # plt.show()

def get_ave_values(time, signal, average_over):
    # 进行均值滤波去噪
    smooth_list=[]
    myfilter=[]
    filter_window=average_over
    for i in range(len(signal)):
        if len(myfilter) < filter_window:  # 与滤波窗口大小作比较
            myfilter.append( signal[i])
        else:
            smooth_data = np.mean(myfilter)
            myfilter.pop(0)  # 减去第一个数据，随后加一个新的数，形成一个动态的均值滤波器
            myfilter.append(signal[i])
            # raw_list.append(raw_data)
            smooth_list.append(smooth_data)
    return time,smooth_list

def plot_signal_plus_average(time, signal, average_over=5):
    fig, ax = plt.subplots(figsize=(15, 3))
    time_ave, signal_ave = get_ave_values(time, signal, average_over)
    ax.plot(time, signal, label='signal')
    ax.plot(signal_ave, label='time average (n={})'.format(5))
    ax.set_xlim([time[0], time[-1]])
    ax.set_ylabel('Signal Amplitude', fontsize=18)
    ax.set_title('Signal + Time Average', fontsize=18)
    ax.set_xlabel('Time', fontsize=18)
    ax.legend()
    # plt.show()


def get_fft_values(y_values,N):
    xf = np.arange(len(y_values))  # 频率
    f_values = xf[range(int(N / 2))]
    fft_values_ = fft(y_values)
    fft_values = 2.0 / N * np.abs(fft_values_[0:N // 2])
    return f_values, fft_values


def plot_fft_plus_power(time, signal):
    N = len(signal)
    fig, ax = plt.subplots(figsize=(15, 3))
    variance = np.std(signal) ** 2
    time_ave, signal_ave = get_ave_values(time, signal, average_over=5)
    f_values, fft_values = get_fft_values(signal_ave, N)
    fft_power = variance * abs(fft_values) ** 2  # FFT power spectrum
    ax.plot(f_values, fft_values, 'r-', label='Fourier Transform')
    ax.plot(f_values, fft_power, 'k--', linewidth=1, label='FFT Power Spectrum')
    ax.set_xlabel('Frequency [Hz / year]', fontsize=18)
    ax.set_ylabel('Amplitude', fontsize=18)
    ax.legend()
    # plt.show()

fname = os.path.join("D:\\a_user_file\\data\\1_Pulse Transit Time PPG Dataset", "s1_run.csv")
dataset = []

with open(fname, "r") as f1:
    data = f1.read()
    lines = data.split("\n")
    #lines = lines[1:len(lines) - 1]
    lines = lines[1:3000]
    num = []
    for i in range(len(lines)):
        line_i = lines[i].split(",")
        num.append(int(line_i[4]))
    print(len(num))  # 245274
    for i in range(len(num)):
        if i%5==0:
            dataset.append(int(num[i]))
    print(len(dataset))

time = np.arange(len(dataset))
signal = dataset
scales = np.arange(1, 128)

plot_signal_plus_average(time, signal)
plot_fft_plus_power(time, signal)
plot_wavelet(time, signal, scales)
plt.show()

最后显示的结果为：

8、小波分解重构信号

小波是如何将一个信号分解成它的子频带，并重新构造原始信号呢？这一节将详细介绍：

PyWavelets 提供了两种解析信号的方法：
(1)用pywt.dwt()函数来检索近似系数。然后对检索到的系数应用DWT以获得第二级系数，并继续此过程，直到达到所需的分解级别；
(2)用pywt.wavedec()函数直接和检索所有的细节系数达到某种程度上n。这个函数作为输入原始信号和n水平并返回一组近似系数(第n个水平)和n组细节系数(1到n级)。

8.1、pywt.dwt()函数解构重构信号

import pywt
import numpy as np
import matplotlib.pyplot as plt
import os

# fname是存放数据的目录
fname = os.path.join("D:\\a_user_file\\data\\1_Pulse Transit Time PPG Dataset", "s1_run.csv")

with open(fname, "r") as f1:
    data = f1.read()
    lines = data.split("\n")
    #lines = lines[1:len(lines) - 1]
    lines = lines[1:3000]
    data_set = []
    for i in range(len(lines)):
        line_i = lines[i].split(",")
        data_set.append(int(line_i[4]))
    # print(len(data_set))  
    
signal=data_set[:3000]
(cA1, cD1) = pywt.dwt(signal, 'db2', 'smooth')
reconstructed_signal = pywt.idwt(cA1, cD1, 'db2', 'smooth')

plt.subplot(211)
plt.plot(signal, label='signal')
plt.xlabel('x-采样点', fontproperties='SimHei')
plt.ylabel('y-幅值', fontproperties='SimHei')
plt.title('原始波形', fontproperties='STLITI', fontsize=10)
plt.subplot(212)
plt.plot(reconstructed_signal, label='reconstructed signal', linestyle='--')
plt.xlabel('x-采样点', fontproperties='SimHei')
plt.ylabel('y-幅值', fontproperties='SimHei')
plt.title('合成波形', fontproperties='STLITI', fontsize=10)
plt.show()

运行后的结果显示图为：

上面图像中实线显示为原始数据图像，虚线为pywt.dwt()函数解析后构造出来的信号图像显示，从幅值和轮廓上都可以看出pywt.dwt()函数可以比较完美得构造出原始信号。其中pywt.dwt()函数更多用于低级别系数的重构。

8.2、pywt.wavedec()函数解构重构信号

用9.1所用的数据集进行检验并对比，将中间的信号解构重构函数修改后，程序如下所示：

import pywt
import numpy as np
import matplotlib.pyplot as plt
import os

# fname是存放数据的目录
fname = os.path.join("D:\\a_user_file\\data\\1_Pulse Transit Time PPG Dataset", "s1_run.csv")

with open(fname, "r") as f1:
    data = f1.read()
    lines = data.split("\n")
    #lines = lines[1:len(lines) - 1]
    lines = lines[1:3000]
    data_set = []
    for i in range(len(lines)):
        line_i = lines[i].split(",")
        data_set.append(int(line_i[4]))
    # print(len(data_set))  
    
signal=data_set[:3000]
coeffs = pywt.wavedec(signal, 'db2', level=8)
reconstructed_signal = pywt.waverec(coeffs, 'db2')

plt.subplot(211)
plt.plot(signal, label='signal')
plt.xlabel('x-采样点', fontproperties='SimHei')
plt.ylabel('y-幅值', fontproperties='SimHei')
plt.title('原始波形', fontproperties='STLITI', fontsize=10)
plt.subplot(212)
plt.plot(reconstructed_signal, label='reconstructed signal', linestyle='--')
plt.xlabel('x-采样点', fontproperties='SimHei')
plt.ylabel('y-幅值', fontproperties='SimHei')
plt.title('合成波形', fontproperties='STLITI', fontsize=10)
plt.show()

运行后显示的图像为：

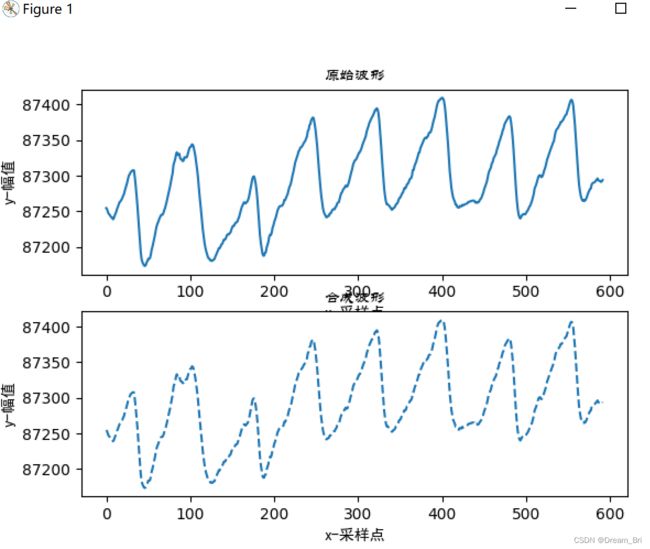
可见，pywt.wavedec()函数也能够很好得将信号重构出来，其中pywt.wavedec()函数更多用于高级别系数的重构。

9、使用离散小波变换去除噪声信号

根据上面内容，我们知道可以将信号分解为近似(低通)和细节(高通)系数。并且可以用这些系数重建信号，我们将得到原始信号。

如果我们在重建的过程中丢掉一些细节系数会怎么样呢？因为细节系数代表的是信号中的高频部分，我们只需要过滤掉这部分频谱，就相当于可以过滤掉高频的噪声信号。

此处我们可以使用pywt.threshold()来删除细节系数，它可以删除了高于给定阈值的系数值。在进行解构信号后，把一些系数设为零，然后重新构造，我们可以从信号中去除高频噪声。

此处，所用的pywt.threshold()函数来删除细节系数的代码显示如下：

def lowpassfilter(signal, thresh = 0.63, wavelet="db4"):
    thresh = thresh*np.nanmax(signal)
    coeff = pywt.wavedec(signal, wavelet, mode="per" )
    coeff[1:] = (pywt.threshold(i, value=thresh, mode="soft" ) for i in coeff[1:])
    reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" )
    return reconstructed_signal

rec = lowpassfilter(signal, 0.4)

10、使用离散小波变换进行信号分类

之前的内容可以看到如何使用连续小波变换和卷积神经网络来对信号进行分类的。其实用离散小波变换也可以进行信号的分类的。

离散小波变换分类思想如下：离散小波变换用于将一个信号分割成不同的子频带，尽可能多的子频带或尽可能多的子频带。如果不同类型的信号表现出不同的频率特性，这种行为上的差异必须表现在一个频率子带中。因此，如果我们从每个子带生成特征，并将这些特征集合作为分类器的输入(Random Forest, Gradient boost, Logistic Regression等)，并利用这些特征训练分类器，那么分类器应该能够区分不同类型的信号。即：将信号进行离散小波变换时，可以分解它的频率子带。并从每个子带中提取特征，作为分类器的输入。

那么，可以从每个子带的数值集中生成什么样的特性呢?当然，这在很大程度上取决于信号的类型和应用程序。但是一般来说，依然有一些最常用的特性。

(1)自回归模型系数值;
(2)熵值:熵值可以用来衡量信号的复杂度;
(3)统计特征如：方差、标准差、均值、中值、第25百分位值、第75个百分位值、均方根值、导数的均值、过零率：即信号通过y = 0的次数。

def calculate_entropy(list_values):
    counter_values = Counter(list_values).most_common()
    probabilities = [elem[1]/len(list_values) for elem in counter_values]
    entropy=scipy.stats.entropy(probabilities)
    return entropy

def calculate_statistics(list_values):
    n5 = np.nanpercentile(list_values, 5)
    n25 = np.nanpercentile(list_values, 25)
    n75 = np.nanpercentile(list_values, 75)
    n95 = np.nanpercentile(list_values, 95)
    median = np.nanpercentile(list_values, 50)
    mean = np.nanmean(list_values)
    std = np.nanstd(list_values)
    var = np.nanvar(list_values)
    rms = np.nanmean(np.sqrt(list_values**2))
    return [n5, n25, n75, n95, median, mean, std, var, rms]

def calculate_crossings(list_values):
    zero_crossing_indices = np.nonzero(np.diff(np.array(list_values) > 0))[0]
    no_zero_crossings = len(zero_crossing_indices)
    mean_crossing_indices = np.nonzero(np.diff(np.array(list_values) > np.nanmean(list_values)))[0]
    no_mean_crossings = len(mean_crossing_indices)
    return [no_zero_crossings, no_mean_crossings]

def get_features(list_values):
    entropy = calculate_entropy(list_values)
    crossings = calculate_crossings(list_values)
    statistics = calculate_statistics(list_values)
    return [entropy] + crossings + statistics

上面代码可以看到有以下四个函数：(1)、计算输入信号熵值的函数；(2)、用来计算一些统计数据的函数，如几个百分位数、平均值、标准差、方差等；(3)、计算过零率和平均过零率的函数；(4)将这三个函数的结果结合起来的函数。

最后一个get_features()函数为任何值列表返回一组12个特性。因此，如果将一个信号分解成10个不同的子带，我们为每个子带生成特征，我们将得到每个信号的10*12 = 120个特征。

参考文本：http://ataspinar.com/2018/12/21/a-guide-for-using-the-wavelet-transform-in-machine-learning/