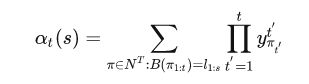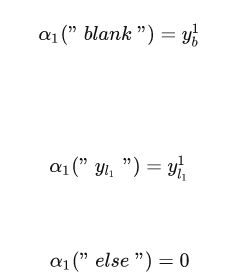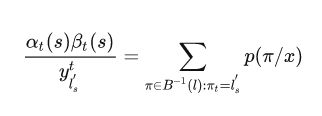【OCR】CTC loss原理
1 CTC loss出现的背景
在图像文本识别、语言识别的应用中,所面临的一个问题是神经网络输出与ground truth的长度不一致,这样一来,loss就会很难计算,举个例子来讲,如果网络的输出是”-sst-aa-tt-e’', 而其ground truth为“state”,那么像之前经常用的损失函数如cross entropy便都不能使用了,因为这些损失函数都是在网络输出与ground truth的长度一致情况下使用的。除了长度不一致的情况之外,还有一个比较难的点在于有多种情况的输出都对应着ground truth,根据解码规则(相邻的重复字符合并,去掉blank), path1: “-ss-t-a-t-e-” 和path2: "–stt-a-tt-e"都可以解码成“state”,与ground truth对应, 也就是many-to-one。为了解决以上问题,CTC loss就产生啦~
2 CTC loss原理
2.1 前序
在说明原理之前,首先要说明一下CTC计算的对象:softmax矩阵,通常我们在RNN后面会加一个softmax层,得到softmax矩阵,softmax矩阵大小是timestep*num_classes, timestep表示的是时间序列的维度,num_class表示类别的维度。
import numpy as np
ts = 12
num_classes = 26+1 #26 for the number of english character, 1 for blank
rnn_output = np.random.random((ts, 16))#16 for hidden node number
w = np.random.random((16,num_classes))
logits = np.matmul(rnn_output,w)#logits: ts*num_classes=[12,27]
#calculate softmax matrix
maxvalue = np.max(logits, axis=1, keepdims=True)
exp = np.exp(logits-maxvalue) #minus maxvalue for avoiding overflow
exp_sum = np.sum(exp, axis=1, keepdims=True)
y = softmax = exp/exp_sum #softmax:ts*num_classes=[12,27]
2.2 forward-backward计算
其实呢,整体过程可以看做是对输入的y也就是softmax做了相应的映射得到解码结果,在希望解码结果尽量正确的情况下(使用概率来衡量),对网络的参数进行梯度下降。

只有在timestep=7时为a的路径才会使用
进行路径的分数计算,所以求偏导的时候只对这部分路径求取就可以啦
path1:“-ss-t-a-t-e-” 第7个timestep为a, path2: "–stt-a-tt-e"第7个timestep也为a, 以a为中点,将这两条路径分别分成两段。
path1_forward: “-ss-t-” path1_backward: “-t-e-”
path2_forward: “–stt-” path2_backward: “-tt-e”
你也会发现 path1_forward+“a”+path2_backward也能够解码成正确的”state", 我们使用path3来表示该路径 , 同样的, path2_forward+“a”+path1_backward也可以解码成正确的“state",我们使用path4表示该路径
在下式中我们考虑中仅仅包含path1,path2, path3, path4
其中表示的是解码后的长度。先看forward部分。
2.2.1 forward部分
这个公式计算的是所有能够解码成的概率,
公式可能一下子不能理解透,举个例子好啦,先看上面的那种情况,也就是特殊情况下的递推公式:
def forward(y, labels):
T,C = y.shape #T: timestep
L = len(labels)
alpha=np.zeros([T,L])
alpha[0,0]=y[0,labels[0]]
alpha[0,1]=y[0,labels[1]]
for t in range(1,T):
for i in range(L):
s= labels[i]
a = alpha[t-1,i]
if i-1>=0:
a += alpha[t-1,i-1]
if i-2>=0 and s!=0 and s!=labels[i-2]:
a +=alpha[t-1,i-2]
alpha[t,i]=a*y[t,s]
return alpha
labels = [0, 19, 0, 20, 0, 1, 0, 20, 0, 5, 0]
alpha = forward(y,labels)
就像刚刚所说,末尾带有blank和不带有blank都是正确的,“-s-t-a-t-e-“和”-s-t-a-t-e"都可以正确解码,所以
p = alpha[-1,lables[-1]]+alpha[-1,lables[-2]]
2.2.2 backward部分
forward讲清楚之后, backward快速的过一遍就好啦

这个公式计算的是所有能够解码成的概率,
上面三个式子是说第T个timestep的解码成”blank“的概率是![]()
, 其他的字符的概率为0, 可以这样理解,如果路径能够解码成正确的”state", 那么第T个timestep的肯定是blank或者"e", 只有这样才能解码正确。 我们可以得到与forward相似的递推式:
套用上面forward的方式去理解,应该不难的~
def backward(y, labels):
T,C = y.shape #T: timestep
L = len(labels)
beta=np.zeros([T,L])
beta[-1,-1]=y[-1,labels[-1]]
beta[-1,-2]=y[-1,labels[-2]]
for t in range(T-2,-1,-1):
for i in range(L):
s= labels[i]
b = beta[t+1,i]
if i+1<L:
b += beta[t+1,i+1]
if i+2<L and s!=0 and s!=labels[i+2]:
b +=beta[t+1,i+2]
beta[t,i]=b*y[t,s]
return beta
labels = [0, 19, 0, 20, 0, 1, 0]
beta = backward(y,labels)
2.3 梯度
求了上面的forward和backward之后,就可以求解梯度啦
所以对求导的话, 仅有当为类别k的那一项不为0, 其余项的偏导都为0

def gradient(y,labels):
T,C = y.shape
L = len(labels)
alpha = forward(y,labels)
beta = backward(y,labels)
p = alpha[-1,-1]+alpha[-1,-2]
gradient = np.zeros([T,V])
for t in range(T):
for c in range(C):
lab = [idx for idx, item in enumerate(labels) if item == c]
for i in lab:
gradient[t, s] += alpha[t, i] * beta[t, i]
gradient[t,c]/=-(y[t,c]**2)
return gradient3
3 CTC loss优缺点
优点:在文本识别和语言识别领域中,能够比较灵活地计算损失,进行梯度下降
缺点:存在假设前提即每个lable相互独立, 因此可以计算路径的概率,才有了接下来的推导过程,但是在很多情况下上下文的label是有关联的,CTC loss很难考虑这一点,不过这些可以通过引入语言模型解码来解决啦~