快速排序
- 算法思想
它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。 - 实现思路
1、首先设定一个分界值,通过该分界值将数组分成左右两部分。
2、将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值。
3、然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
4、重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了。
转载内容(很生动形象)
分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于6的数,再从左往右找一个大于6的数,然后交换他们。这里可以用两个变量i和j,分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵i”和“哨兵j”。刚开始的时候让哨兵i指向序列的最左边(即i=1),指向数字6。让哨兵j指向序列的最右边(即=10),指向数字。
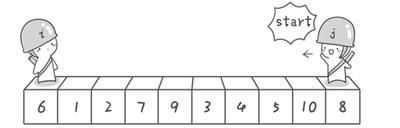
首先哨兵j开始出动。因为此处设置的基准数是最左边的数,所以需要让哨兵j先出动,这一点非常重要。哨兵j一步一步地向左挪动(即j–),直到找到一个小于6的数停下来。接下来哨兵i再一步一步向右挪动(即i++),直到找到一个数大于6的数停下来。最后哨兵j停在了数字5面前,哨兵i停在了数字7面前。
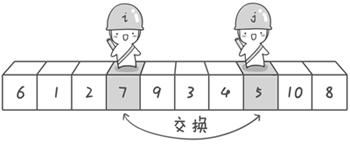
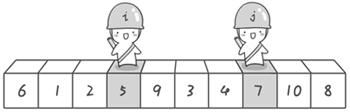
现在交换哨兵i和哨兵j所指向的元素的值。交换之后的序列如下:
6 1 2 5 9 3 4 7 10 8
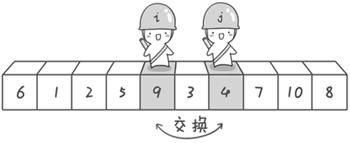
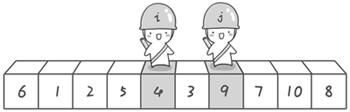
到此,第一次交换结束。接下来开始哨兵j继续向左挪动(再友情提醒,每次必须是哨兵j先出发)。他发现了4(比基准数6要小,满足要求)之后停了下来。哨兵i也继续向右挪动的,他发现了9(比基准数6要大,满足要求)之后停了下来。此时再次进行交换,交换之后的序列如下:
6 1 2 5 4 3 9 7 10 8
第二次交换结束,“探测”继续。哨兵j继续向左挪动,他发现了3(比基准数6要小,满足要求)之后又停了下来。哨兵i继续向右移动,糟啦!此时哨兵i和哨兵j相遇了,哨兵i和哨兵j都走到3面前。说明此时“探测”结束。我们将基准数6和3进行交换。交换之后的序列如下:
3 1 2 5 4 6 9 7 10 8


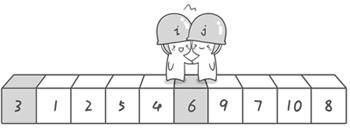
到此第一轮“探测”真正结束。此时以基准数6为分界点,6左边的数都小于等于6,6右边的数都大于等于6。回顾一下刚才的过程,其实哨兵j的使命就是要找小于基准数的数,而哨兵i的使命就是要找大于基准数的数,直到i和j碰头为止。
OK,解释完毕。现在基准数6已经归位,它正好处在序列的第6位。此时我们已经将原来的序列,以6为分界点拆分成了两个序列,左边的序列是“3 1 2 5 4”,右边的序列是“9 7 10 8”。接下来还需要分别处理这两个序列(递归思想)。因为6左边和右边的序列目前都还是很混乱的。不过不要紧,我们已经掌握了方法,接下来只要模拟刚才的方法分别处理6左边和右边的序列即可。现在先来处理6左边的序列现吧。
左边的序列是“3 1 2 5 4”。请将这个序列以3为基准数进行调整,使得3左边的数都小于等于3,3右边的数都大于等于3。好了开始动笔吧
如果你模拟的没有错,调整完毕之后的序列的顺序应该是:
2 1 3 5 4
OK,现在3已经归位。接下来需要处理3左边的序列“2 1”和右边的序列“5 4”。对序列“2 1”以2为基准数进行调整,处理完毕之后的序列为“1 2”,到此2已经归位。序列“1”只有一个数,也不需要进行任何处理。至此我们对序列“2 1”已全部处理完毕,得到序列是“1 2”。序列“5 4”的处理也仿照此方法,最后得到的序列如下:
1 2 3 4 5 6 9 7 10 8
对于序列“9 7 10 8”也模拟刚才的过程,直到不可拆分出新的子序列为止。最终将会得到这样的序列,如下
1 2 3 4 5 6 7 8 9 10
到此,排序完全结束。细心的同学可能已经发现,快速排序的每一轮处理其实就是将这一轮的基准数归位,直到所有的数都归位为止,排序就结束了。下面上个霸气的图来描述下整个算法的处理过程。
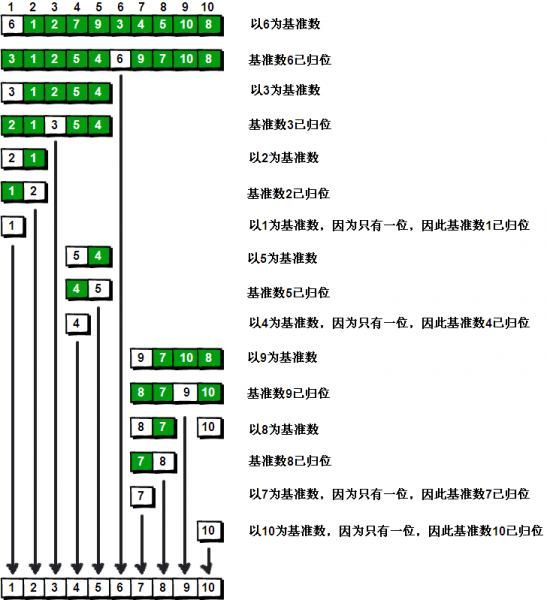
快速排序之所比较快,因为相比冒泡排序,每次交换是跳跃式的。每次排序的时候设置一个基准点,将小于等于基准点的数全部放到基准点的左边,将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换,交换的距离就大的多了。代码如下:
public static void qsort(int[] arr, int start, int end){
int pvot = start;
int left = start;
int right = end;
if (arr == null || arr.length < 2) {
return;
}
if(left > right){
return;
}
while(left < right){
//先看右边,依次往左递减
while( (left < right) && (arr[right] >= arr[pvot]) ){
right--;
}
//再看左边,依次往右递增
while( (left < right) && (arr[left] <= arr[pvot]) ) {
left++;
}
System.out.println("left="+left+",right="+right);
if(left < right){
int tmp = arr[right];
arr[right] = arr[left];
arr[left] = tmp;
}else{
//最后将基准为与i和j相等位置的数字交换 也可以放在while 外面执行
int tmp = arr[right];
arr[right] = arr[pvot];
arr[pvot] = tmp;
}
}
//递归调用左半数组
qsort(arr,start,left-1);
//递归调用右半数组
qsort(arr,right+1,end);
}
int[] arr = {6, 1, 2, 7, 9, 3, 4, 5, 10, 8};
qsort(arr,0 ,arr.length-1);
for (int i : arr) {
System.out.print(i + " ");
}
输出:
left=3,right=7
left=4,right=6
left=5,right=5
left=2,right=2
left=1,right=1
left=4,right=4
left=8,right=9
left=8,right=8
left=7,right=7
1 2 3 4 5 6 7 8 9 10 如果是逆序数组,比如[9 8 7 6 5 4 3 2 1],选取第一个元素作为基准点,那么第一次循环,左游标要执行到最右边,而右游标执行一次,然后两者进行交换。这也会划分成很多的子数组。
解决方案:三数取中法
public class QuickSort {
public static void main(String[] args) {
int[] arr = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
quickSort(arr, 0, arr.length - 1);
System.out.println("排序结果:" + Arrays.toString(arr));
}
/**
* @param arr
* @param left 左指针
* @param right 右指针
*/
public static void quickSort(int[] arr, int left, int right) {
if (left < right) {
// 获取枢纽值,并将其放在当前待处理序列末尾
dealPivot(arr, left, right);
// 枢纽值被放在序列末尾
int pivot = right - 1;
int i = left; // 左指针
int j = right - 1; // 右指针
while (true) {
while (arr[++i] < arr[pivot]) {
}
while (j > left && arr[--j] > arr[pivot]) {
}
if (i < j) {
swap(arr, i, j);
} else {
break;
}
}
if (i < right) {
swap(arr, i, right - 1);
}
quickSort(arr, left, i - 1);
quickSort(arr, i + 1, right);
}
}
/**
* 处理枢纽值
*
* @param arr
* @param left
* @param right
*/
public static void dealPivot(int[] arr, int left, int right) {
int mid = (left + right) / 2;
if (arr[left] > arr[mid]) {
swap(arr, left, mid);
}
if (arr[left] > arr[right]) {
swap(arr, left, right);
}
if (arr[right] < arr[mid]) {
swap(arr, right, mid);
}
swap(arr, right - 1, mid);
}
/**
* 交换元素通用处理
*
* @param arr
* @param a
* @param b
*/
private static void swap(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}