Level_2(2)题目整理

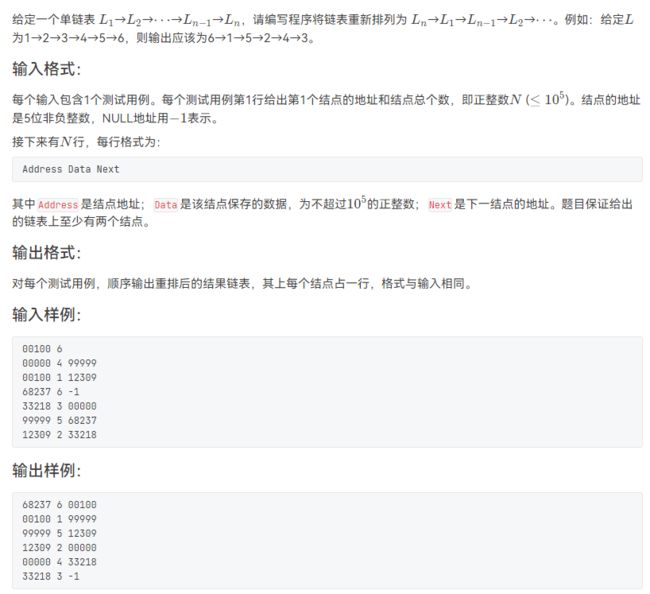
L2-022 重排链表（模拟❗）

#include
using namespace std;
const int maxn = 1e5 + 10;

struct node{
	int data;
	int next;
}node[maxn];

int st,num,t;

int main(){
	cin >> st >> num;
	for(int i = 1; i <= num; i++){
		cin >> t;
		cin >> node[t].data >> node[t].next;
	}
	//记住顺序链表的地址 
	int orpos[maxn]; int idx = 0,head = st;
	while(head != -1)
	{
		orpos[idx] = head;
		head = node[head].next;
//		cout << idx << " " << orpos[idx] << endl;
		idx ++;
	} 
	//注意：orpos数组是从下标0开始的 
	int f = -1,l = 0, r = idx - 1;
	for(int i = 1; i < idx; i++){
		if (f == -1){
			node[orpos[r--]].next = orpos[l];
		}
        else {
			node[orpos[l++]].next = orpos[r];
		}
        f = f*(-1);
	}
	node[orpos[l]].next = -1; //把最后一个节点指向-1 
	t = orpos[idx - 1]; //记录原来的最后一个节点，输出时为第一个 
	
	for(int i = 1; i < idx; i++){
		printf("%05d %d %05d\n", t, node[t].data, node[t].next);
        t = node[t].next;
	}
	printf("%05d %d %d\n", t, node[t].data, node[t].next);
    return 0;
} 

L2-023 图着色问题

直接按照题意做就行：
（1）注意是必须使用K种颜色（不是小于等于k）
（2）没有给出边数的最大值（应该尽量开的大点，否则导致测试点5一直段错误）
思路：
对于每种颜色方案，我们采用color数组存下来，然后判断每个点与其邻接点有没有相同的颜色。

#include
using namespace std;
const int N = 510;
int h[N*4],ne[N*10000],to[N*1100];//没有给出边的最大条数（真坑）
int idx;
int color[N];
int v,e,kk;
void add(int u,int v){
	ne[++idx] = h[u];
	to[idx] = v;
	h[u] = idx;
}
set<int>st;
bool check(){	
	for(int fir = 1; fir <= v; fir++){
		
		for(int i = h[fir]; i != 0; i = ne[i]){
			int j = to[i];
			if(color[fir] == color[j]){
				return false;
			}
		}
	}
	return true;
}
int main(){
	cin >> v >> e >> kk;
	for(int i = 1; i <= e; i++){
		int u,v;
		cin >> u >> v;
		add(u,v);
		add(v,u);
	}
	
	int n;
	cin >> n;
	for(int k = 1; k <= n; k++){
		st.clear();
		for(int i = 1; i <= v; i++){
			cin >> color[i];
			st.insert(color[i]);
		}
		if(st.size() != kk){ //真坑
			cout << "No" << endl;
		}
		else if(check()){
			cout << "Yes" << endl;	
		}else{
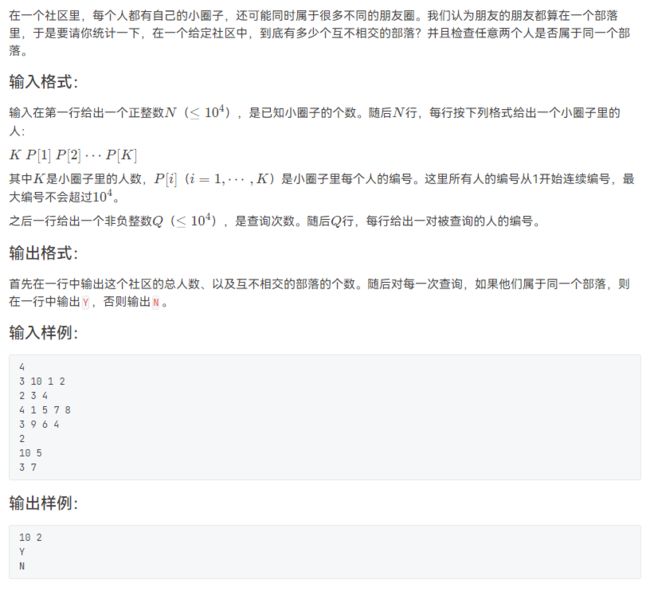
			cout << "No" << endl;
		}
	}
} 

L2-024 部落(并查集)

直接使用并查集将每个部落的所有人进行合并，因为编号是连续的，所有最后部落总人数就是最大编号，然后直接查询两人是否是同一个祖先即可判断是不是同一部落

#include
using namespace std;
const int N = 1E4 + 100;
int fa[N];
set<int>st;
int group[N];
int maxn = 0;
void init(){
	for(int i = 1; i < N; i++){
		fa[i] = i;
	}
}
int find(int x){
	if(fa[x] == x){
		return x;
	}
	return fa[x] = find(fa[x]);
}
void merge(int x,int y){
	int fx = find(x);
	int fy = find(y);
	if(fx != fy){
		fa[fx] = fy;
	}
}
int main(){
	init();
	int n;
	cin >> n;
	while(n--){
		int k;
		cin >> k;
		for(int i = 1; i <= k; i++){
			cin >> group[i];
			st.insert(group[i]);
			maxn = max(maxn,group[i]);
		}
		for(int i = 2; i <= k; i++){
			merge(group[1],group[i]);
		}
	}
	int type = 0;
	for(int i = 1; i <= maxn; i++){
		if(fa[i] == i){
			type++;
		} 
	}
	cout << maxn << " " << type << endl;
	int q;
    cin >> q;
	for(int i = 1; i <= q; i++){
		int x,y;
		cin >> x >> y;
		if(find(x) == find(y)){
			cout << "Y" << endl;
		}else{
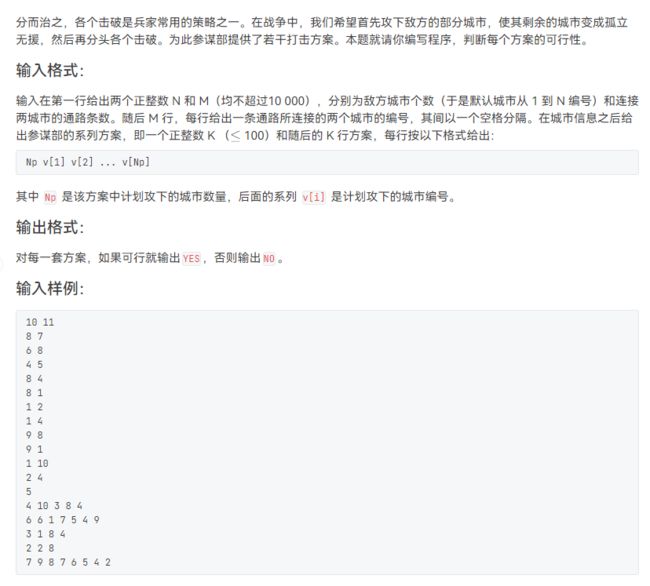
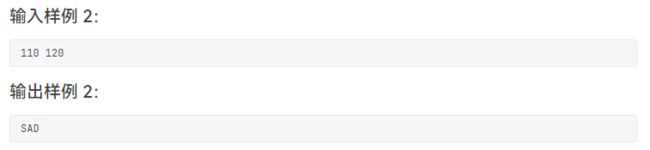
			cout << "N" << endl; 
		}
	}
}

L2-025 分而治之（与 L2-023差不多，邻接表遍历）

思路：
邻接表存储邻接关系，采用vis数组记录每次攻击的城市，然后看未被攻击的 城市是否还有相连的即可

#include
using namespace std;
const int N = 1e4 + 100;
int h[N],ne[N*2],to[N*2];
bool vis[N];
int idx;
int n,m;
void add(int u, int v){
	ne[++idx] = h[u];
	to[idx] = v;
	h[u] = idx; 
}
bool isOk(){
	for(int fir = 1;fir <= n; fir++){
		
		if(vis[fir] == false){
			for(int i = h[fir]; i != 0; i =ne[i]){
				int j = to[i];
				if(vis[j] == false){
					return false;
				}
			}
		}
		
	}
	return true;
}
int main(){
	cin >> n >> m;
	for(int i = 1; i <= m; i++){
		int u,v;
		cin >> u >> v;
		add(u,v);
		add(v,u);
	}
	
	int k;
	cin >> k;
	for(int i = 1; i <= k; i++){
		
		for(int i = 1; i <= n;i++){
			vis[i] = false;
		}
		
		int num; cin >> num;
		
		for(int i = 1; i <= num; i++){
			int x;
			cin >> x;
//			cout << x;
			vis[x] = true;
		} 
		
		if(isOk()){
			cout << "YES" << endl;	
		}else{
			cout << "NO" << endl;
		}
	}
}

L2-026 小字辈（求树的深度）

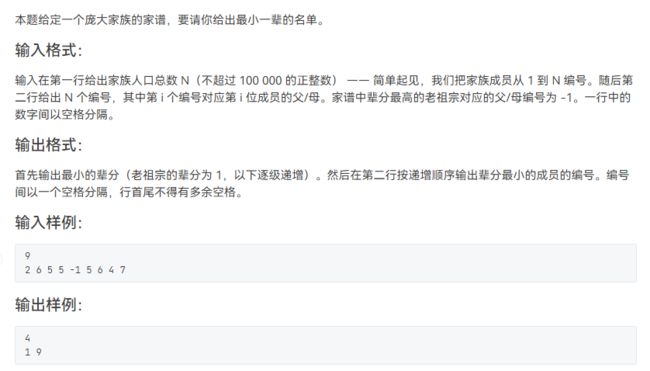
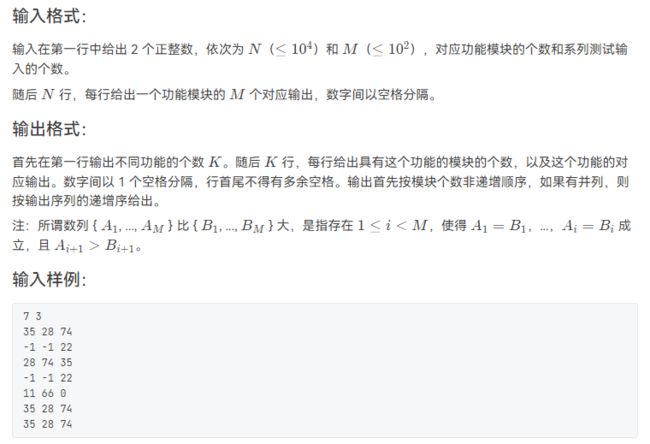
先找到-1的节点，记住此节点编号，即为最高的老祖宗，然后以此为根节点进行深度优先遍历，求所有点的深度，即为辈分 ，最后输出最小的辈分，并统计个数即可

#include
using namespace std;
const int N = 1e5 + 100;
int h[N],ne[N*2],to[N*2];
bool vis[N];
int depth[N];
int idx;
int n,m;
int son[N];
void add(int u, int v){
	ne[++idx] = h[u];
	to[idx] = v;
	h[u] = idx; 
}
void dfs(int root,int dep){
	depth[root] = dep;
	vis[root] = true;
	for(int i = h[root]; i != 0; i = ne[i]){
		int j = to[i];
		if(!vis[j]){
			dfs(j,dep + 1);
		}
	}
}
int main(){
	cin >> n;
	int root = 0;
	for(int i = 1; i <= n; i++){
		int x; cin >> x;
		if(x == -1){
			root = i;
		}else{
			add(x,i);
			add(i,x);
		}
	}
	dfs(root,1);
	int maxn = 0;
	for(int i = 1; i <= n; i++){
//		cout << depth[i] <<" ";
		maxn = max(maxn,depth[i]);
	}
	int tol = 0;
	for(int i = 1; i <= n; i++){
		if(depth[i] == maxn){
			son[++tol] = i; 
		}
	}
	
	cout << maxn << endl;
	sort(son + 1,son + tol + 1);
	for(int i = 1; i <= tol; i++){
		if(i == tol){
			cout << son[i];	
		}else{
            cout << son[i] << " ";
        }
	}

	
}

L2-027 名人堂与代金券(处理)

思路：直接根据题意进行即可
首先统计所有需要发的代金卷的面值，我们需要进行结构体排序，先按照成绩，再按照账号
题目没有要求最后不能输出多余空行，所以没必要控制
：
对于相同排名的处理很巧妙，只要与前面的人分数相同，那么我们一直不去更新这个当前排名，只有与前面的人分数不同时再去更新为自己当前的排名（前面无论有多少人，都不会影响我本应该的排名，所以直接设置为自己排序后所处的位置即可）

#include
using namespace std;
int n,g,k;
struct info{
	string id;
	int score;	
}p[10010];
bool cmp(info o1,info o2){
	if(o1.score == o2.score){
		return o1.id < o2.id;
	}else{
		return o1.score > o2.score;
	}
}
int main(){
	cin >> n >> g >> k;
	for(int i = 1; i <= n; i++){
		cin >> p[i].id >> p[i].score;
	}
	sort(p+1,p + 1+n,cmp);
	int money = 0;
	for(int i = 1; i <= n; i++){
		if(p[i].score >= g){
			money += 50;
		}else if(p[i].score >= 60){
			money += 20;
		}
	}
	cout << money << endl; 
	int cur = 0;
	for(int i = 1; i <= n; i++){
		if(p[i].score != p[i - 1].score){
			cur = i; //只要分数一直相等，那么就不需要改变排名，只有不相等的时候，为自己原本的排名（妙） 
		}
		if(cur > k){
			break;
		}
		cout << cur<<" "<<p[i].id<<" "<<p[i].score<<endl;
	}
	
}

L2-028 秀恩爱分得快（❗vector二维数组，输入处理❗大模拟❓）

借鉴博客
处理起来比较麻烦，但是题意还是很好懂得
思路：
（1）首先由于存在+0，-0我们不能使用int输入，我们应该使用string或者char进行读入
（2）我们不能边存图片信息边处理，这样的话会超时，我们先存下来图片信息，最后根据给出的情侣编号去计算我们需要的

#include
#include
typedef long long ll;
using namespace std;
bool flag[1005];


int read() {
	int input = 0, sign = 0;
	char a = getchar();
	while ((a < '0' || a > '9') && a != '-')
		a = getchar();
	if (a == '-') {
		sign = 1;
		a = getchar();
	}
	while (a >= '0' && a <= '9') {
		input = input * 10 + a - '0';
		a = getchar();
	}
	flag[input] = sign;     
	return input;
}

int main() {
	int n, m;
	while (scanf("%d%d", &n, &m) != EOF) {
		memset(flag, false, sizeof(flag));
		vector<vector<int> >p(n);	//存储所有照片
		vector<double> PA(n, 0.0), PB(n, 0.0);	//与A的亲密度，与B的亲密度 (初始化了含有n个0.0的vector)
		int coloum;
		for (int i = 0; i < m; ++i) {
			scanf("%d", &coloum);
			p[i].resize(coloum);
			for (int j = 0; j < coloum; ++j) {
				p[i][j] = read();
			}
		}
		int A, B;
		A = read(), B = read();
		double MAXA = 0.0, MAXB = 0.0;
		for (int i = 0; i < m; ++i) {
			bool FindA = find(p[i].begin(), p[i].end(), A) != p[i].end();	//查找A
			bool FindB = find(p[i].begin(), p[i].end(), B) != p[i].end();	//查找B
			if (FindA || FindB) {
				for (int j = 0; j < p[i].size(); ++j) {
					if (FindA && flag[A] != flag[p[i][j]]) { // 有A 且性别不一样
						PA[p[i][j]] += (double)1.0 / p[i].size();	//亲密度累加
						MAXA = max(MAXA, PA[p[i][j]]);	//最大亲密度
					} else if (FindB && flag[B] != flag[p[i][j]]) {
						PB[p[i][j]] += (double)1.0 / p[i].size();
						MAXB = max(MAXB, PB[p[i][j]]);
					}
				}
			}
		}
		if (MAXA == PA[B] && MAXB == PB[A]) {	//彼此亲密度最高
			printf("%s%d %s%d\n", flag[A] ? "-" : "", A, flag[B] ? "-" : "", B);
		} else {
			for (int i = 0; i < n; i++) {
				if (PA[i] == MAXA) {
					printf("%s%d %s%d\n", flag[A] ? "-" : "", A, flag[i] ? "-" : "", i);
				}
			}
			for (int i = 0; i < n; i++) {
				if (PB[i] == MAXB) {
					printf("%s%d %s%d\n", flag[B] ? "-" : "", B, flag[i] ? "-" : "", i);
				}
			}
		}
	}
	
}

L2-029 特立独行的幸福（模拟）

思路：

预处理出来给定区间之间的数，用vector存储转换过程中依赖于此数的数，并记录有多少数依赖于此数，并将依赖于别人的数进行标记。

if(find(process.begin(),process.end(),sum) != process.end()){
			break;
}

查找在vector中是否存在sum这个数。

#include 
#include
#include
using namespace std;
const int N = 1e5 + 10;
bool vis[N];
int f[N];
int a;
int b;
bool isprime(int x){
	if(x == 1){
		return false;
	}
	for(int i = 2; i <= x/i; i++){
		if(x % i == 0){
			return false;	
		}
	}
	return true;
}

void getLevel(int num) {

	vector<int> process;
	int temp = num;

	int sum = 0;
	while(temp != 1) {
		int sum = 0;
		while(temp != 0) {
			int t = temp % 10;
			sum += t * t;
			temp = temp / 10;
		}
		temp = sum;
		if(find(process.begin(),process.end(),sum) != process.end()){
			break;
		}
		process.push_back(sum);
		vis[sum] = true;
	}
	if(temp == 1){
		f[num] = process.size();
	}
}

int main() {
	cin >> a >> b;
	for(int i = a; i <= b; i++) {
		getLevel(i);
	}
	bool ok = false;
	for(int i = a; i <= b; i++){
		if(!vis[i] && f[i]){
			ok = true;
			if(isprime(i)){
				cout << i << " " << 2 * f[i] << endl;
			}else{
				cout << i << " " << f[i] << endl;
			}
		}
	}
	if(!ok){
		cout << "SAD";
	}
}

L2-030 冰岛人(❓)

引自

#include 
#include
#include
using namespace std;
const int N = 1e5 + 10;
struct info {
	char sex;
	string fa;
};
map<string,info> person;
bool judge(string a,string b){
	int fa_a = 1,fa_b;
	for(string A = a; !A.empty(); A = person[A].fa,fa_a++){
		fa_b = 1;
		for(string B = b; !B.empty(); B = person[B].fa,fa_b++){
			if(fa_a >= 5 && fa_b >=5){
				return true;  
			}
			if(A==B &&(fa_a < 5 || fa_b < 5)){
				return false;
			}
		}
	}
	return true;
}
int main() {
	int n;
	cin >> n;
	for(int i = 1; i <= n; i++) {
		string a,b;
		cin >> a >> b;
		if(b.back() == 'n') { //儿子 sson
			person[a] = {'m',b.substr(0,b.size() - 4)};
		} else if(b.back() == 'r') { //女儿 sdottir
			person[a] = {'f',b.substr(0,b.size() - 7)};  //记住性别和父亲的名字 
		} else {
			person[a].sex = b.back();
		}
	}
	
	int m;
	cin >> m;
	for(int i = 1; i <= m; i++){
		string a,c,b;
		cin >> a >> c >> b >> c;
		if(person.find(a) == person.end() || person.find(b) == person.end()){//存在一方名字不在名单中 
			cout << "NA" << endl; 
		}else if(person[a].sex == person[b].sex){
			cout << "Whatever" << endl;
		}else{
			if(judge(a,b)){
				cout << "Yes" << endl;
			}else{
				cout << "No" << endl;
			}
		}
	} 
	
}

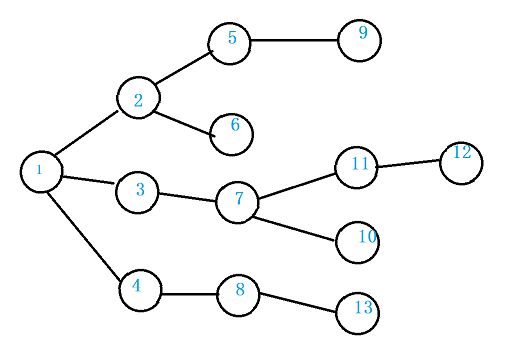
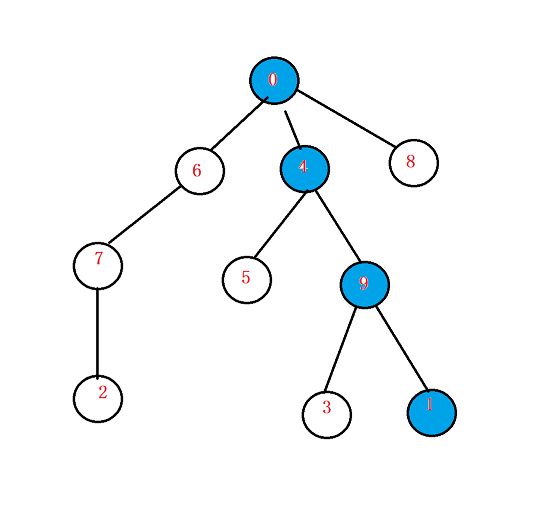
L2-031 深入虎穴（邻接表求深度）

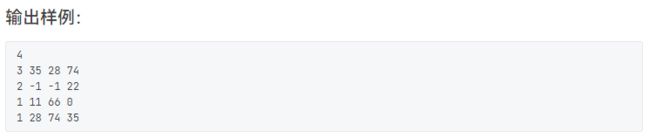
：由上图可知距离最远的就是途中最深节点的深度，并且题目中说了结果唯一，所以直接求最深节点的深度和节点编号即可，但是在输入的时候我们需要找到入度为0的点，我们将所有被指向的点标记，剩下的点即为遍历时可以当根节点进行遍历的点。

#include 
#include
#include
using namespace std;
const int N = 1e5 + 10;
int h[N],ne[N],to[N];
int idx,n;
bool f[N];
bool vis[N];
int depth[N];
int maxn = 0,pos = 0;
void add(int a,int b){
	ne[++idx] = h[a];
	to[idx] = b;
	h[a] = idx;
}
void dfs(int u,int dep){
	vis[u] = true;depth[u] = dep;
	for(int i = h[u]; i != 0; i = ne[i]){
		int j = to[i];
		if(!vis[j]){
			dfs(j,dep+1);
		}
	}
}
int main() {
	cin >> n;
	for(int i = 1; i <= n; i++){
		int k; cin >> k;
		for(int j = 1; j <= k; j++){
			int x;
			cin >> x;
			add(i,x);
			f[x] = true;
		}
	}	
	
	for(int i = 1; i <= n; i++){
		if(!f[i]){
			dfs(i,1);
		}
	}
	
	for(int i = 1; i <= n; i++){
		if(depth[i] > maxn){
			maxn = depth[i];
			pos = i;
		}
//		cout << depth[i];
	}	
	cout << pos;
}

L2-032 彩虹瓶（栈）

注意点：
多次使用同一数组或者变量每次都需要初始化（真的服了，debug了半天（测试点1错了无数次））

#include 
#include
#include
using namespace std;
const int N = 1e3 + 10;
int n,m,k;
bool vis[N];
stack<int>st;
int a[N];
void clear() {
	while(st.size()) {
		st.pop();
	}
}

void init() {
	for (int i = 0; i < N; i ++) vis[i] = false;
}

bool check() {
	init();
	clear();
	int cur = 1;
	for(int i = 1; i <= n; i++) {
		if(a[cur] != i) {
			if(vis[i] == true && !st.empty() && st.top() != i) {
				return false;
			} else if(vis[i] == true && !st.empty() && st.top() == i) {
				st.pop();
			} else {
				while(a[cur] != i) {
					if(st.size() >=m){
						return false;
					}
					st.push(a[cur]);
					vis[a[cur]] = true;
					cur++;
				}
				vis[a[cur]] == true;
				cur++;
				
			}
		}else{
			vis[i] == true;
			cur++;
		}
	}
	if(!st.empty()){
		return false;
	}
	return true;
}
int main() {
	cin >> n >> m >> k;
	for(int i = 1; i <= k; i++) {
		for(int j = 1; j <= n; j++) {
			cin >> a[j];
		}
		
		if(check()) {
			cout << "YES" << endl;
		} else {
			cout << "NO" << endl;
		}
	}
}

L2-033 简单计算器(栈+模拟)

思路：很明显就是栈，题目说的很明白了，按照所给步骤进行模拟即可
注意多个栈名区分清楚，注意细节即可。

#include 
#include
#include
using namespace std;
const int N = 1e3 + 10;
int n;
stack<int>num;
stack<char>op;
int main() {
	cin >> n;
	for(int i = 1; i <= n; i++){
		int x;
		cin >> x;
		num.push(x);
	}
	for(int i = 1; i <= n - 1; i++){
		char ch;
		cin >> ch;
		op.push(ch);
	}
	
	while(num.size() >= 2 && op.size()){
		int a = num.top();num.pop();
		int b = num.top();num.pop();
		char ops = op.top();op.pop();  //Attention extiguish stack name 
		int c = 0;
		if(ops == '/'){
			if(a == 0){
				cout << "ERROR: " <<  b  << "/0" << endl;
				return 0;
			}else{
				c = b / a;
				num.push(c);
			}
		}else if(ops == '+'){
			c = b + a;
			num.push(c);
		}else if(ops == '-'){
			c = b - a;
			num.push(c);
		}else{
			c = a * b;
			num.push(c);
		}
	}
	cout << num.top();
}

L2-034 口罩发放

L2-035 完全二叉树的层序遍历(树的遍历)

我们可以借助完全二叉树的特点：直接递归求解即可，最后为根节点，其

#include
using namespace std;
int n, k;
int tree[1010];
void dfs(int index) {
    if(index <= n) {
        dfs(index * 2);
        dfs(index * 2 + 1);
		cin>>tree[index];
    }
}
int main() {
    cin>>n;
    dfs(1);
    for(int i = 1 ; i <= n ; i++)
        cout<<tree[i]<<(i == n ? "\n" : " "); 
    return 0;
}

L2-036 网红点打卡攻略(无向图+set)

思路：首先对于给出的线路关系，采用临界矩阵进行存储，然后对于给出的每组方案，判断是否行（需要注意的是：每个地方只能去且仅去一次，我们采用set的去重特性，那所有去的点存到set中，只要最后set的大小是n，那么肯定所有点都去了并且只去了一次）然后顺便进行更新最小花费，并累加可行方案即可。

#include
#include
using namespace std;
int g[210][210];
int n,m;
int main() {
	cin >> n >> m;
	for(int i = 1; i <= m; i++) {
		int x,y,z;
		cin >> x >> y >> z;
		g[x][y] = g[y][x] = z;
	}
	int k;
	cin >> k;
	int ans = 1e9;
	int tol = 0,idx;
	for(int i = 1; i <= k; i++) {
		queue<int> q;
		set<int> st;
		int num,sum = 0;
		cin >> num;
		for(int i = 1; i <= num; i++) {
			int v;
			cin >> v;
			q.push(v);
			st.insert(v);
		}
		if(num != n || st.size() != n) { //num!=n(代表访问的点有重复或者不够)
			continue;
		}
		bool ok = true;
		int now = 0;
		while(!q.empty())  {
			int vq = q.front();
			q.pop();
			if(g[now][vq] == 0) {
				ok = false;
			}
			sum += g[now][vq];
			now = vq;
		}
		if(g[now][0] == 0){
			ok = false;
		}
		if(!ok) {
			continue;//不可行直接跳过
		}
		sum += g[now][0];  //注意回家也需要花费
		tol++;
		if(sum < ans){
			ans = sum;
			idx = i;
		}
	}
	
	cout << tol << endl;
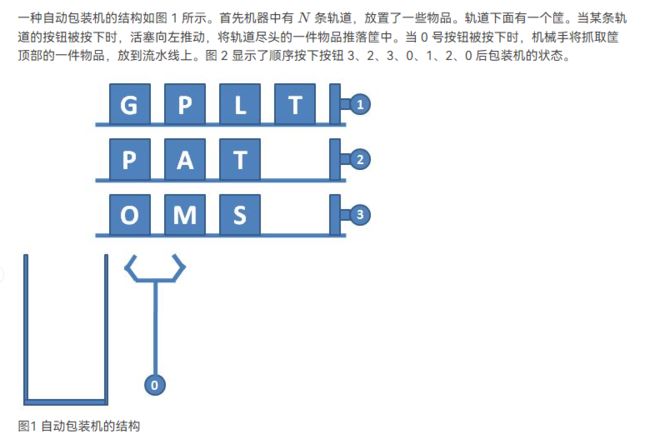
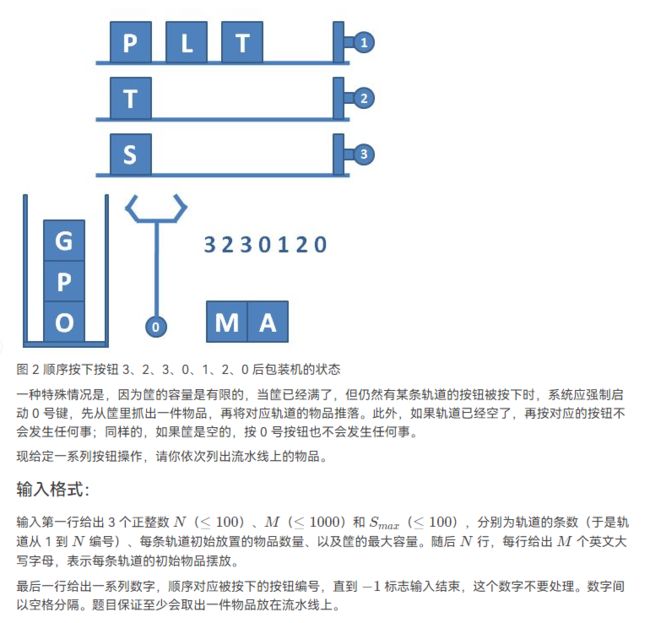
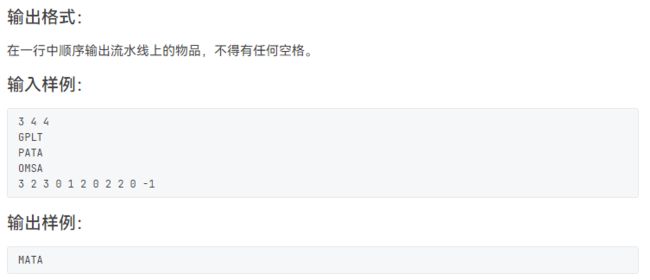
	cout << idx << " " << ans;
	
}

L2-037 包装机(栈+队列)

很明显：物体进入筐中就是出队入栈，从筐中放到流水线上就是出栈（需要注意判空）

#include
using namespace std;
#include
#include
int n,m,smax;

int main(){
	cin >> n >> m >> smax;
	stack<char> st;
	queue<char> q[n +10];
	for(int i = 1; i <= n; i++){
		char ch;
		for(int j = 1; j <= m; j++){
			cin >> ch;
			q[i].push(ch);
		}
	}
	
	while(1){
		int x;
		cin >> x;
		if(x == -1){
			break;
		}
		if(x == 0 &&  st.size()){
			cout << st.top();
			st.pop();
		}
		if(x > 0 && st.size() >= smax &&q[x].size()){
			cout << st.top();
			st.pop();
			st.push(q[x].front());
			q[x].pop();
		}else if(x > 0 && st.size() < smax && q[x].size()){
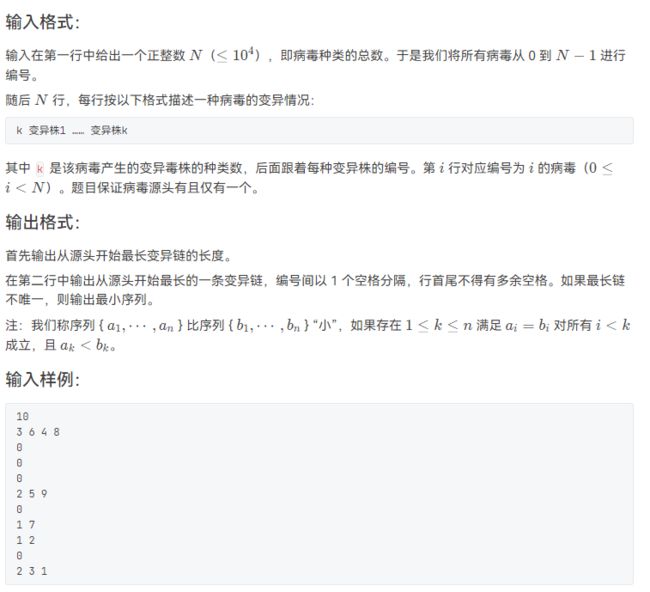
			st.push(q[x].front());
			q[x].pop();
		}
	}
}

L2-038 病毒溯源(树的遍历)

就是从根节点开始找一条最长且字典序最小的路径输出

#include
using namespace std;
#include
#include
int n;
const int N = 1e4 + 10;
int idx;
string path[N];
bool f[N];
bool vis[N];
int h[N],ne[N],to[N];
int chu[N];
int cnt;
void add(int u,int v){
	ne[++idx] = h[u];
	to[idx] = v;
	h[u] = idx;
}

void dfs(int u,string p){
	vis[u] = true;
	if(chu[u] == 0){
		path[++cnt] = p;
		return;
	}
	for(int i = h[u]; i != 0; i = ne[i]){
		int j = to[i];
		if(!vis[j]){
			string ch = to_string(j);
			dfs(j,p + ch);
		}
	}
	
}

int main(){
	cin >> n;
	for(int i = 0; i < n; i++){
		int num;
		cin >> num;
		for(int j = 1; j <= num; j++){
			int x;
			cin >> x;
			f[x] = true;
			add(i,x);
			chu[i]++;
		}
	}
	for(int i = 0; i < n; i++){
		if(!f[i]){
			string cc = to_string(i);  
			dfs(i,cc);
		}
	}
	string s[cnt + 10];
	int len = 0,tol = 0;
	sort(path + 1,path + 1 + cnt);
	for(int i = 1; i <= cnt; i++){
		string str = path[i];
		int l = str.length();
		len = max(len,l);
	}
	string ans;
	for(int i = 1; i <= cnt; i++){
		string str = path[i];
		int l = str.length();
		if(l == len){
			ans = str;
			break;
		}
	}
	cout << len << endl;
	for(int i = 0; i < ans.length(); i++){
		if(i == ans.length() - 1){
			cout << ans[i];
		}else{
			cout << ans[i] << " ";
		}
	}
}

Ac代码如下：

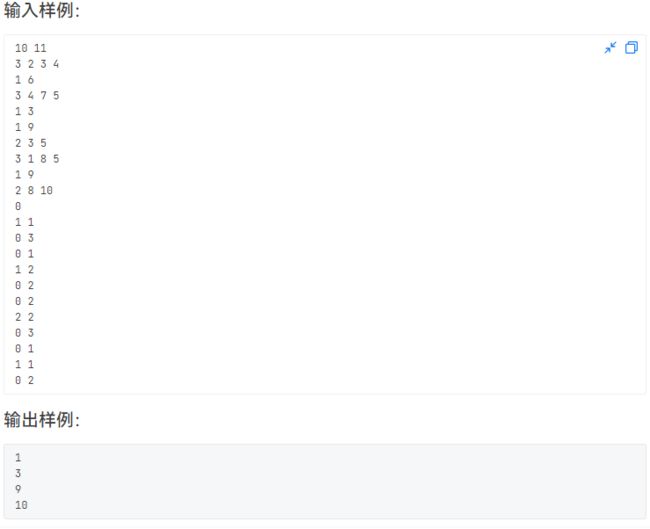
L2-039 清点代码库（map+vector+(计数、去重、排序)⭐⭐⭐）

题意还是很好立交的，就是不太会实现，对STL掌握的不太熟练，很多用法都不会，只会比较简单的/(ㄒoㄒ)/~~
就是统计不同功能模块的个数和重复出现的次数，我们需要进行去重并进行按照要求的规则进行排序
（1）去重的实现
set和map都可以实现去重的功能，但是我们同时需要统计数量，但是对于map中的键值对中的键我们需要采用vector作为键，（太神奇了）

引自

#include
#include
using namespace std;
map<vector<int>, int> mp;  //用map统计
struct node {
	vector<int> v;
	int num;
};

vector<node> ans;
bool cmp(node o1,node o2) {
	if(o1.num == o2.num) return o1.v < o2.v;
	return o1.num > o2.num;
}
int main() {
	int n,m;
	cin >> n >> m;
	for(int i = 1; i <= n; i++) {
		vector<int> v;
		for(int j = 1; j <= m; j++) {
			int x;
			cin >> x;
			v.push_back(x);
		}
		if(mp.count(v)) {
			mp[v]++;
		} else {
			mp[v] = 1;
		}
	}
	cout << mp.size() << endl;
	for(auto i :mp) { //存到vector中排序
		node node;
		node.num = i.second;
		node.v = i.first;
		ans.push_back(node);
	}
	sort(ans.begin(),ans.end(),cmp);

	for(auto i : ans) {
		cout << i.num;
		for(auto j :i.v) {
			cout << " " << j;
		}
		cout << endl;
	}

}

L2-040 哲哲打游戏(模拟/vector)

注意：最后一行需要输出最后到达的编号。 其他地方进行模拟即可，需要注意vector的下标默认是从0开始的，所以我们需要-1（数组的形式只能用来遍历vector，不可以进行赋值）

#include
#include
using namespace std;
int n,m;
//0.选择，直接去
//1.读取存档，回到存档位置
//2.读档输出即可 
int record[10010];
int main() {
	cin >> n >> m;
	vector<vector<int> >vec(n + 10);
	for(int i = 1; i <= n; i++){
		int num;cin >> num;
		for(int j = 1; j <= num; j++){
			int x;
			cin >> x;
			vec[i].push_back(x);
		}
	}
	int cur = 1;
	for(int i = 1; i <= m; i++){
		int op,x;
		cin >> op >> x;
		if(op == 0){ //选择 
			cur = vec[cur][x - 1]; //在当前位置选择了x 
		}else if(op == 1){  //存档 
			cout << cur << endl;
			record[x - 1] = cur;
		}else{
			cur = record[x - 1]; //读档 
		} 
	}
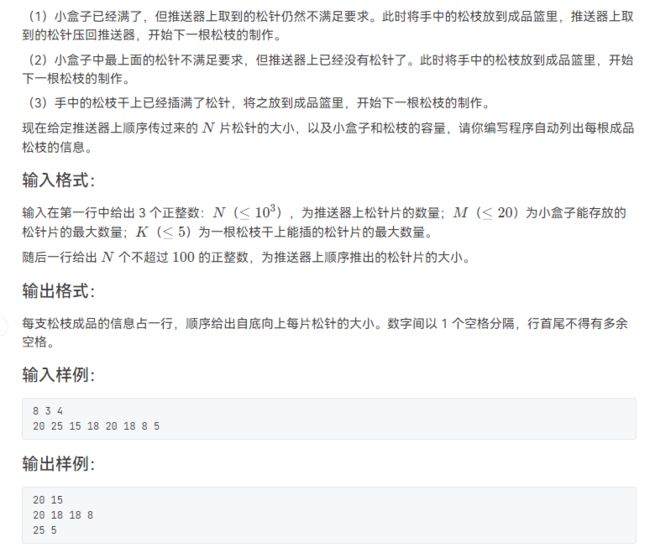
	cout << cur; 

}

L2-041 插松枝（模拟/❗注意理清思路再写❗）

模拟题，一定理清思路再写代码，防止把自己写晕，尽量写的简洁

#include
using namespace std;
queue<int> q;
stack<int> st;
int n,m,k;
queue<int> goods;
int main() {
	cin >> n >> m >> k; //m小盒子 k松树
	for(int i = 1; i <= n; i++) {
		int x;
		cin >> x;
		q.push(x);
	}
	int count = 0,last = 1010;
	while(q.size()){
		if(st.size() && st.top() <= last){
			if(count == 0){
				cout << st.top();
			}else{
				cout << " " << st.top();
			}
			last = st.top();
			st.pop();
			count ++;
		}else if(q.front() <= last){
			if(count == 0){
				cout << q.front();
			}else{
				cout << " " << q.front();
			}
			last = q.front();
			count++;
			q.pop();
		}else if(st.size() < m){
			st.push(q.front());
			q.pop();
		}
		if(count == k || (st.size() == m && q.front() > last && st.top() >last)){ //一个成品输出 
			cout << endl;
			count = 0;
			last = 1010;
		}
		
		
	}
	
	while(st.size()){
		if(st.top() <= last && count < k){
			if(count){
				cout << " " << st.top();
			}else{
				cout <<  st.top();
			}
			last = st.top();
			st.pop();
			count ++;
		}else{
			cout << endl;
			count = 0;//新的一件产品
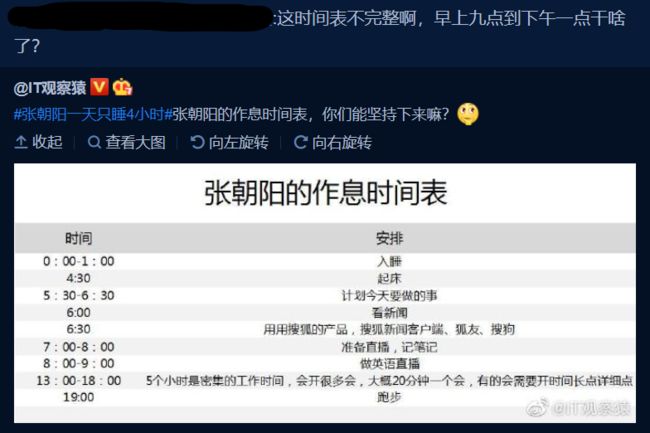
			last = 1010; 
		}
	} 

}

L2-042 老板的作息表(输入格式处理，结构体排序⭐⭐⭐技巧)

采用scanf进行控制输入和输出十分简单，需要注意的是，我们在进行排序的时候，可以直接按照3个字段进行排序，不用进行转换（实在太麻烦，还容易出错），多想想
想明白了，简单而且写代码很方便

#include
using namespace std;
const int N = 1e5 + 10;

queue<int> q;
stack<int> st;
int n,m,k;

struct node {
	int h1,m1,s1;
	int h2,m2,s2;
} t[N];

bool cmp(node t1,node t2) {
	if(t1.h1 == t2.h1) {
		if(t1.m1 == t2.m1) {
			return t1.s1 < t2.s1;
		} else {
			return t1.m1 < t2.m1;
		}
	} else {
		return t1.h1 < t2.h1;
	}
}
int main() {
	scanf("%d",&n);
	int preh = 0,prem = 0,pres = 0;
	for(int i = 1; i <= n; i++) {
		scanf("%d:%d:%d - %d:%d:%d",&t[i].h1,&t[i].m1,&t[i].s1,&t[i].h2,&t[i].m2,&t[i].s2);
	}
	sort(t+1,t+1+n,cmp);
	
	for(int i = 1; i <= n; i++) {
		if(t[i].h1 != preh || t[i].m1 != prem || t[i].s1 != pres) {
			printf("%02d:%02d:%02d - %02d:%02d:%02d\n",preh,prem,pres,t[i].h1,t[i].m1,t[i].s1);
		}
		preh = t[i].h2;  prem = t[i].m2;  pres = t[i].s2;
	}
	if(preh != 23 || prem != 59 || pres != 59) {
		printf("%02d:%02d:%02d - %02d:%02d:%02d\n",preh,prem,pres,23,59,59);
	}
}

L2-043 龙龙送外卖(记忆化搜索⭐⭐⭐)

如果需要回到起点的话，那么所有要走的边需要走2遍，要是不需要回到起点，我们为了路程最短，只需要将走的路程*2-maxn即可

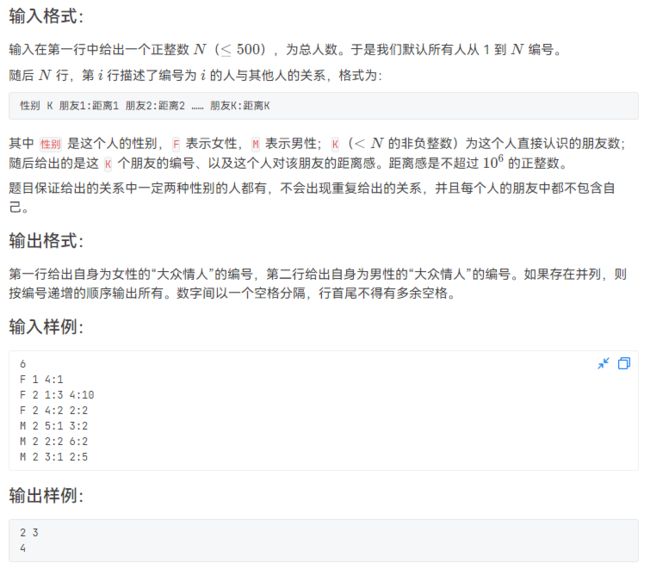
L2-044 大众情人(Floyed⭐⭐⭐)

只要能想到用Floyed实现题目中所说的借助其他店进行更新就很简单了

#include
using namespace std;

int a[510][510];  //记录i对j的距离感 
int dis[510];  //存异性最无感的大小 
int sex[510];  //存每个人的性别（1为女性，-1为男性） 
int n;

//初始化，除了自己对自己的距离感为0，其他人都为无穷 
void init() {
	for(int i = 0; i <= 500; i++) {
		for(int j = 0; j <= 500; j++) {
			if(i != j) {
				a[i][j] = 1e9 + 10; 
			}else{
				a[i][j] = 0;
			}
		}
	}
}
int main() {
	init();
	cin >> n;
	for(int i = 1; i <= n; i++) {
		char s;
		cin >> s;
		if(s == 'F') {
			sex[i] = 1;
		} else {
			sex[i] = -1;
		}
		int k;
		cin >> k;
		
		for(int j = 1; j <= k; j++) {
			int id,lev;
			scanf("%d:%d",&id,&lev); //一般这种读入比较适合用scanf() 
			a[i][id] = lev;  //注意不具有双向性 
		} 
	}

	//Floyed算法，借助中间点进行更新 
	for(int k = 1; k <= n; k++) {
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= n; j++) {
				a[i][j] = min(a[i][j],a[i][k] + a[k][j]);
			}
		}
	}

	for(int i = 1; i <= n; i++) {
		dis[i] = 0;
		for(int j = 1; j <= n; j++) {
			if(sex[i] != sex[j]) { //找异性中最无感的（最大的）
				dis[i] = max(dis[i],a[j][i]);
			}
		}
	}

	//找女性中(最无感的人距离感越小，异性缘越好)
	int gmin_dis = 2e9;
	int g_num = 0;
	for(int i = 1; i <= n; i++) {
		if(sex[i] == 1) {
			gmin_dis = min(gmin_dis,dis[i]);
		}
	}
	for(int i = 1; i <= n; i++) {
		
		if(dis[i] == gmin_dis) {
			if(sex[i] == 1 && g_num == 0) { //注意性别条件 
				cout << i;
			} else {
				cout << " " << i;
			}
			g_num++;
		}
	}
	cout << endl;


	//找男性中(最无感的人距离感越小，异性缘越好)
	int bmin_dis = 2e9;
	int b_num = 0;
	for(int i = 1; i <= n; i++) {
		if(sex[i] == -1) {
			bmin_dis = min(bmin_dis,dis[i]);
		}
	}
	for(int i = 1; i <= n; i++) {
		if(sex[i] == -1 && dis[i] == bmin_dis) {  //一定要判断性别，要不会错 
			if(b_num == 0) {
				cout << i;
			} else {
				cout << " " << i;
			}
			b_num++;
		}
	}
}