ABAQUS材料子程序学习(线性随动硬化塑性)
ABAQUS材料子程序学习(线性随动硬化塑性)
- 前言
-
- 塑性力学增量形式实现
- umat 程序
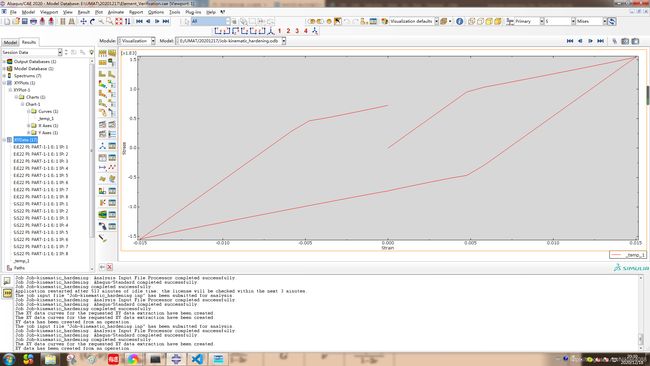
- 结果
前言
继续塑性本构,随动硬化塑性。
记录自己学习abaqus软件umat子程序的t过程,本文主要参考了《非线性本构关系在ABAQUS中的实现》第四章和技术邻的视频课程“非线性各向同性强化弹塑性umat子程序教程”
塑性力学增量形式实现
计算过程中,体应变和体应力是弹性关系 Δ σ v = K ⋅ Δ ε v (1) {Δσ_v}={K}\cdot{Δε_v}\tag{1} Δσv=K⋅Δεv(1)
K K K为体积模量, K = E 3 ( 1 − ν ) K=\cfrac{E}{3(1-ν)} K=3(1−ν)E , Δ ε v = Δ ε 11 + Δ ε 22 + Δ ε 33 Δε_v=Δε_{11}+Δε_{22}+Δε_{33} Δεv=Δε11+Δε22+Δε33
所以在下面的讨论中只考虑偏应力张量和偏应力张量
试应力: σ t r ′ ( t ) = σ ′ ( t ) + C ′ : Δ ε ′ (2) \bm{σ^{tr'}(t)=σ'(t)+\mathbb{C'}:Δε'}\tag{2} σtr′(t)=σ′(t)+C′:Δε′(2)
线性随动硬化塑性的屈服函数: f = [ 3 2 ( σ ′ − α ′ ) : ( σ ′ − α ′ ) ] 1 2 − σ y = σ ^ M i s e s − σ y (3) f=\left[\frac{3}{2}\bm{(σ'-α'):(σ'-α')} \right]^{\frac{1}{2}}-σ_y={\widehat{σ}_{Mises}}-σ_y\tag{3} f=[23(σ′−α′):(σ′−α′)]21−σy=σ Mises−σy(3)
其中, α ′ \bm{α'} α′为背应力,三维问题6个分量; σ y σ_y σy初始屈服强度, σ ^ M i s e s {\widehat{σ}_{Mises}} σ Mises 有效应力的Mises等效应力。
线性随动硬化模型:Mises等效背应力与等效塑性增量成正比
Δ α M i s e s = c Δ ε ˉ p Δ α = 2 3 c Δ ε p (4) Δα_{Mises}=cΔ\bar{ε}^p\\ \quad\\\tag{4} \bm{Δα}=\frac{2}{3}cΔ\bm{ε^p} ΔαMises=cΔεˉpΔα=32cΔεp(4)
c c c随动硬化系数。
α ′ \bm{α'} α′背应力作为状态变量存在STATEV(NSTATV)中,提取 α ′ \bm{α'} α′背应力并计算试应力的有效屈服应力 σ M i s e s t r {σ_{Mises}^{tr}} σMisestr
判断 σ M i s e s t r {σ}_{Mises}^{tr} σMisestr 与 σ y {σ_y} σy 关系:
若 σ M i s e s t r < σ y {σ}_{Mises}^{tr}<{σ_y} σMisestr<σy : σ ( t + Δ t ) = σ t r ( t ) \bm{σ(t+Δt)}=\bm{σ^{tr}(t)} σ(t+Δt)=σtr(t)
一致切线刚度矩阵,为弹性刚度矩阵
D D S D D E ( i , j ) = [ 2 G + λ λ λ 0 0 0 λ 2 G + λ λ 0 0 0 λ λ 2 G + λ 0 0 0 0 0 0 G 0 0 0 0 0 0 G 0 0 0 0 0 0 G ] (5) \bm{DDSDDE}(i,j) =\left [\begin{matrix} 2G+λ&λ&λ&0&0&0 \\ λ&2G+λ&λ&0&0&0 \\ λ&λ& 2G+λ&0&0&0 \\ 0&0&0& G&0&0 \\ 0&0&0&0& G&0 \\ 0&0&0&0&0 &G \end{matrix} \right ]\tag{5} DDSDDE(i,j)=⎣⎢⎢⎢⎢⎢⎢⎡2G+λλλ000λ2G+λλ000λλ2G+λ000000G000000G000000G⎦⎥⎥⎥⎥⎥⎥⎤(5)
若 σ M i s e s t r ≥ σ y {σ}_{Mises}^{tr}≥{σ_y} σMisestr≥σy ,计算新增的 Δ ε ˉ p Δ\bar{ε}^p Δεˉp
Δ ε ˉ p = σ M i s e s t r − σ y ( c + 3 G ) Δ\bar{ε}^p=\frac{{σ}_{Mises}^{tr}-σ_{y}}{(c+3G)} Δεˉp=(c+3G)σMisestr−σy
根据正交流动法则:
Δ ε p = Δ ε ˉ p 3 2 σ ^ ′ σ ^ M i s e s = Δ ε ˉ p 3 2 σ ^ t r ′ σ ^ M i s e s t r \bm{Δε^p}=Δ\bar{ε}^p\frac{3}{2}\frac{\bm{\widehatσ'}}{\widehatσ_{Mises}}=Δ\bar{ε}^p\frac{3}{2}\frac{\bm{\widehatσ^{tr'}}}{\widehatσ_{Mises}^{tr}} Δεp=Δεˉp23σ Misesσ ′=Δεˉp23σ Misestrσ tr′
代入(4)更新背应力,STATEV(1)……STATEV(NTENS)
应力增量=弹性刚度矩阵×弹性应变增量
Δ σ = D e : Δ ε e \bm{Δσ=D_e:Δε^e} Δσ=De:Δεe
弹性应变=总应变-塑性应变增量
Δ σ = D e : ( Δ ε − Δ ε p ) (6) \bm{Δσ=D_e:(Δε-Δε^p)}\tag{6} Δσ=De:(Δε−Δεp)(6)
屈服后一致切线刚度矩阵:
将 d ε p \bm{dε^p} dεp 用 d ε \bm{dε} dε 表示出来,再代回式(6)就可求出屈服后的DDSDDE(NTENS,NTENS)
一致性条件
{ f ( σ ′ , α ) = 0 f ( σ ′ + d σ ′ , α + d α ) = 0 ⟹ ∂ f ∂ σ ′ d σ ′ + ∂ f ∂ α d α = 0 (7) \begin{cases} f(\bm{σ'},\bm{α})=0 \\ f(\bm{σ'}+d\bm{σ'},\bm{α}+d\bm{α})=0 \end{cases} \implies \frac{\partial f}{\partial \bm{σ'}} \bm{dσ'}+\frac{\partial f}{\partial \bm{\alpha}} \bm{d\alpha}=0\tag{7} {f(σ′,α)=0f(σ′+dσ′,α+dα)=0⟹∂σ′∂fdσ′+∂α∂fdα=0(7)
其中: { ∂ f ∂ σ ′ = ∂ [ 3 2 ( σ ′ − α ) : ( σ ′ − α ) ] 1 2 ∂ σ ′ = 6 σ ^ M i s e s ( σ ′ − α ) ∂ f ∂ α = − ∂ f ∂ σ ′ (8) \begin{cases} \Large{\frac{\partial f}{\partial \bm{σ'}}}=\frac{\partial \left[\frac{3}{2}\bm{(σ'-α):(σ'-α)} \right]^{\frac{1}{2}}}{\partial \bm{σ'}}=\frac{6}{{\widehat{σ}_{Mises}}}\bm{(σ'-α)} \\\tag{8} \quad\\ \Large \frac{\partial f}{\partial \bm{α}}= -\frac{\partial f}{\partial \bm{σ'}} \end{cases} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧∂σ′∂f=∂σ′∂[23(σ′−α):(σ′−α)]21=σ Mises6(σ′−α)∂α∂f=−∂σ′∂f(8)
(4)、(6)和(8)代入(7):
∂ f ∂ σ ′ d σ ′ = c ∂ f ∂ σ ′ d ε p d σ ′ = c d ε p D e ′ : ( d ε ′ − d ε p ) = c d ε p D e ′ ⋅ d ε ′ = c I : d ε p + D e ′ : d ε p D e ′ : d ε ′ = ( c I + D e ′ ) : d ε p D e ′ : ( I − 1 3 I ^ ) : d ε = ( c I + D e ) : d ε p (9) \begin{aligned} &\frac{\partial f}{\partial \bm{σ'}}\bm{dσ'}=c\frac{\partial f}{\partial \bm{σ'}} \bm{dε^p}\\ \quad\\ & \bm{dσ'}=c \bm{dε^p}\\ \quad\\ & \bm{D'_e:(dε'-dε^p)}=c \bm{dε^p}\\ \quad\\ & \bm{D'_e\cdot dε'}=c \bm{I : dε^p}+ \bm{D'_e: dε^p}\\ \quad\\ & \bm{D'_e: dε'}=(c \bm{I}+ \bm{D'_e}):\bm{dε^p}\\ \quad\\ & \bm{D'_e}: \bm{(I}-\frac{1}{3}\bm{\hat{I})}: \bm{dε}=(c \bm{I}+ \bm{D_e}): \bm{dε^p} \end{aligned}\tag{9} ∂σ′∂fdσ′=c∂σ′∂fdεpdσ′=cdεpDe′:(dε′−dεp)=cdεpDe′⋅dε′=cI:dεp+De′:dεpDe′:dε′=(cI+De′):dεpDe′:(I−31I^):dε=(cI+De):dεp(9)
其中: I = δ i k δ j l e ⃗ i e ⃗ j e ⃗ k e ⃗ l \bm{I}=\delta_{ik}\delta_{jl}\bm{\vec e_i \vec e_j \vec e_k \vec e_l} I=δikδjleiejekel 四阶单位张量, I ^ = δ i j δ k l e ⃗ i e ⃗ j e ⃗ k e ⃗ l \bm{\hat{I}}=\delta_{ij}\delta_{kl}\bm{\vec e_i \vec e_j \vec e_k \vec e_l} I^=δijδkleiejekel
(注: I : A = δ i k δ j l e ⃗ i e ⃗ j e ⃗ k e ⃗ l : A n m e ⃗ n e ⃗ m = δ i k δ j l δ k n δ l m A n m e ⃗ i e ⃗ j = δ i k δ j l A k l e ⃗ i e ⃗ j = A i j e ⃗ i e ⃗ j \bm{I:A}=\delta_{ik}\delta_{jl}\bm{\vec e_i \vec e_j \vec e_k \vec e_l}:A_{nm}\bm{\vec e_n \vec e_m }=\delta_{ik}\delta_{jl}\delta_{kn}\delta_{lm}A_{nm}\bm{\vec e_i \vec e_j }=\delta_{ik}\delta_{jl}A_{kl}\bm{\vec e_i \vec e_j }=A_{ij}\bm{\vec e_i \vec e_j } I:A=δikδjleiejekel:Anmenem=δikδjlδknδlmAnmeiej=δikδjlAkleiej=Aijeiej)
(注: I ^ : A = δ i j δ k l e ⃗ i e ⃗ j e ⃗ k e ⃗ l : A n m e ⃗ n e ⃗ m = δ i j δ k l δ k n δ l m A n m e ⃗ i e ⃗ j = δ i j A k k e ⃗ i e ⃗ j \bm{\hat{I}:A}=\delta_{ij}\delta_{kl}\bm{\vec e_i \vec e_j \vec e_k \vec e_l}:A_{nm}\bm{\vec e_n \vec e_m }=\delta_{ij}\delta_{kl}\delta_{kn}\delta_{lm}A_{nm}\bm{\vec e_i \vec e_j }=\delta_{ij}A_{kk}\bm{\vec e_i \vec e_j } I^:A=δijδkleiejekel:Anmenem=δijδklδknδlmAnmeiej=δijAkkeiej)
再代入(6):
d σ ′ = { D e ′ − D e ′ : ( c I + D e ′ ) − 1 : D e ′ } : ( I − 1 3 I ^ ) : d ε d σ V = K I ^ : d ε (10) \begin{aligned} \bm{dσ'}&=\left\{\bm{D'_e}-\bm{D'_e}:(c \bm{I}+ \bm{D'_e})^{-1}:\bm{D'_e} \right\}: \bm{(I}-\frac{1}{3}\bm{\hat{I})}:\bm{dε}\\ \bm{dσ_V}&=K\bm{\hat{I}}:\bm{dε}\tag{10} \end{aligned} dσ′dσV={De′−De′:(cI+De′)−1:De′}:(I−31I^):dε=KI^:dε(10)
因此: d σ = { [ D e ′ − D e ′ : ( c I + D e ′ ) − 1 : D e ′ ] : ( I − 1 3 I ^ ) + K I ^ } : d ε (11) \bm{dσ}=\left\{\left[\bm{D'_e}-\bm{D'_e}:(c \bm{I}+ \bm{D'_e})^{-1}:\bm{D'_e} \right]: \bm{(I}-\frac{1}{3}\bm{\hat{I})}+K\bm{\hat{I}}\right\}:\bm{dε}\tag{11} dσ={[De′−De′:(cI+De′)−1:De′]:(I−31I^)+KI^}:dε(11)
推导过程保持张量计法
A = [ A 11 , 11 A 11 , 22 A 11 , 33 A 11 , 12 A 11 , 23 A 11 , 13 A 11 , 21 A 11 , 32 A 11 , 31 A 22 , 11 A 22 , 22 A 22 , 33 A 22 , 12 A 22 , 23 A 22 , 13 A 22 , 21 A 22 , 32 A 22 , 31 A 33 , 11 A 33 , 22 A 33 , 33 A 33 , 12 A 33 , 23 A 33 , 13 A 33 , 21 A 33 , 32 A 33 , 31 A 12 , 11 A 12 , 22 A 12 , 33 A 12 , 12 A 12 , 23 A 12 , 13 A 12 , 21 A 12 , 32 A 12 , 31 A 23 , 11 A 23 , 22 A 23 , 33 A 23 , 12 A 23 , 23 A 23 , 13 A 23 , 21 A 23 , 32 A 23 , 31 A 13 , 11 A 13 , 22 A 13 , 33 A 13 , 12 A 13 , 23 A 13 , 13 A 13 , 21 A 13 , 32 A 13 , 31 A 21 , 11 A 21 , 22 A 21 , 33 A 21 , 12 A 21 , 23 A 21 , 13 A 21 , 21 A 21 , 32 A 21 , 31 A 32 , 11 A 32 , 22 A 32 , 33 A 32 , 12 A 32 , 23 A 32 , 13 A 32 , 21 A 32 , 32 A 32 , 31 A 31 , 11 A 31 , 22 A 31 , 33 A 31 , 12 A 31 , 23 A 31 , 13 A 31 , 21 A 31 , 32 A 31 , 31 ] \bm{A}=\left[\begin{array}{ccc:ccc:ccc} A_{11,11}&A_{11,22}&A_{11,33}&A_{11,12}&A_{11,23}&A_{11,13}&A_{11,21}&A_{11,32}&A_{11,31}\\ A_{22,11}&A_{22,22}&A_{22,33}&A_{22,12}&A_{22,23}&A_{22,13}&A_{22,21}&A_{22,32}&A_{22,31}\\ A_{33,11}&A_{33,22}&A_{33,33}&A_{33,12}&A_{33,23}&A_{33,13}&A_{33,21}&A_{33,32}&A_{33,31}\\\hdashline A_{12,11}&A_{12,22}&A_{12,33}&A_{12,12}&A_{12,23}&A_{12,13}&A_{12,21}&A_{12,32}&A_{12,31}\\ A_{23,11}&A_{23,22}&A_{23,33}&A_{23,12}&A_{23,23}&A_{23,13}&A_{23,21}&A_{23,32}&A_{23,31}\\ A_{13,11}&A_{13,22}&A_{13,33}&A_{13,12}&A_{13,23}&A_{13,13}&A_{13,21}&A_{13,32}&A_{13,31}\\\hdashline A_{21,11}&A_{21,22}&A_{21,33}&A_{21,12}&A_{21,23}&A_{21,13}&A_{21,21}&A_{21,32}&A_{21,31}\\ A_{32,11}&A_{32,22}&A_{32,33}&A_{32,12}&A_{32,23}&A_{32,13}&A_{32,21}&A_{32,32}&A_{32,31}\\ A_{31,11}&A_{31,22}&A_{31,33}&A_{31,12}&A_{31,23}&A_{31,13}&A_{31,21}&A_{31,32}&A_{31,31}\\ \end{array}\right] A=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡A11,11A22,11A33,11A12,11A23,11A13,11A21,11A32,11A31,11A11,22A22,22A33,22A12,22A23,22A13,22A21,22A32,22A31,22A11,33A22,33A33,33A12,33A23,33A13,33A21,33A32,33A31,33A11,12A22,12A33,12A12,12A23,12A13,12A21,12A32,12A31,12A11,23A22,23A33,23A12,23A23,23A13,23A21,23A32,23A31,23A11,13A22,13A33,13A12,13A23,13A13,13A21,13A32,13A31,13A11,21A22,21A33,21A12,21A23,21A13,21A21,21A32,21A31,21A11,32A22,32A33,32A12,32A23,32A13,32A21,32A32,32A31,32A11,31A22,31A33,31A12,31A23,31A13,31A21,31A32,31A31,31⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
D e ′ = [ 2 G 0 0 0 0 0 0 0 0 0 2 G 0 0 0 0 0 0 0 0 0 2 G 0 0 0 0 0 0 0 0 0 G 0 0 G 0 0 0 0 0 0 G 0 0 G 0 0 0 0 0 0 G 0 0 G 0 0 0 G 0 0 G 0 0 0 0 0 0 G 0 0 G 0 0 0 0 0 0 G 0 0 G ] \bm{D'_e}=\left[\begin{array}{ccc:ccc:ccc} 2G &0&0&0&0&0&0&0&0\\ 0&2G&0&0&0&0&0&0&0\\ 0&0&2G&0&0&0&0&0&0\\\hdashline 0 &0&0&G&0&0&G&0&0\\ 0&0&0&0&G&0&0&G&0\\ 0&0&0&0&0&G&0&0&G\\\hdashline 0 &0&0&G&0&0&G&0&0\\ 0&0&0&0&G&0&0&G&0\\ 0&0&0&0&0&G&0&0&G\\ \end{array}\right] De′=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡2G0000000002G0000000002G000000000G00G000000G00G000000G00G000G00G000000G00G000000G00G⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
D e ′ + c I = [ 2 G + c 0 0 0 0 0 0 0 0 0 2 G + c 0 0 0 0 0 0 0 0 0 2 G + c 0 0 0 0 0 0 0 0 0 G + c 0 0 G 0 0 0 0 0 0 G + c 0 0 G 0 0 0 0 0 0 G + c 0 0 G 0 0 0 G 0 0 G + c 0 0 0 0 0 0 G 0 0 G + c 0 0 0 0 0 0 G 0 0 G + c ] \bm{D'_e+cI}=\left[\begin{array}{ccc:ccc:ccc} 2G+c &0&0&0&0&0&0&0&0\\ 0&2G+c&0&0&0&0&0&0&0\\ 0&0&2G+c&0&0&0&0&0&0\\\hdashline 0 &0&0&G+c&0&0&G&0&0\\ 0&0&0&0&G+c&0&0&G&0\\ 0&0&0&0&0&G+c&0&0&G\\\hdashline 0 &0&0&G&0&0&G+c&0&0\\ 0&0&0&0&G&0&0&G+c&0\\ 0&0&0&0&0&G&0&0&G+c\\ \end{array}\right] De′+cI=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡2G+c0000000002G+c0000000002G+c000000000G+c00G000000G+c00G000000G+c00G000G00G+c000000G00G+c000000G00G+c⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
[ D e ′ + c I ] − 1 = [ 1 2 G + c 0 0 0 0 0 0 0 0 0 1 2 G + c 0 0 0 0 0 0 0 0 0 1 2 G + c 0 0 0 0 0 0 0 0 0 G + c ( 2 G + c ) c 0 0 − G ( 2 G + c ) c 0 0 0 0 0 0 G + c ( 2 G + c ) c 0 0 − G ( 2 G + c ) c 0 0 0 0 0 0 G + c ( 2 G + c ) c 0 0 − G ( 2 G + c ) c 0 0 0 − G ( 2 G + c ) c 0 0 G + c ( 2 G + c ) c 0 0 0 0 0 0 − G ( 2 G + c ) c 0 0 G + c ( 2 G + c ) c 0 0 0 0 0 0 − G ( 2 G + c ) c 0 0 G + c ( 2 G + c ) c ] \left[\bm{D'_e+cI} \right]^{-1}=\left[\begin{array}{ccc:ccc:ccc} \frac{1}{2G+c} &0&0&0&0&0&0&0&0\\ 0&\frac{1}{2G+c} &0&0&0&0&0&0&0\\ 0&0&\frac{1}{2G+c} &0&0&0&0&0&0\\\hdashline 0 &0&0&\frac{G+c}{(2G+c)c} &0&0&\frac{-G}{(2G+c)c}&0&0\\ 0&0&0&0&\frac{G+c}{(2G+c)c}&0&0&\frac{-G}{(2G+c)c}&0\\ 0&0&0&0&0&\frac{G+c}{(2G+c)c}&0&0&\frac{-G}{(2G+c)c}\\\hdashline 0 &0&0&\frac{-G}{(2G+c)c}&0&0&\frac{G+c}{(2G+c)c}&0&0\\ 0&0&0&0&\frac{-G}{(2G+c)c}&0&0&\frac{G+c}{(2G+c)c}&0\\ 0&0&0&0&0&\frac{-G}{(2G+c)c}&0&0&\frac{G+c}{(2G+c)c}\\ \end{array}\right] [De′+cI]−1=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡2G+c10000000002G+c10000000002G+c1000000000(2G+c)cG+c00(2G+c)c−G000000(2G+c)cG+c00(2G+c)c−G000000(2G+c)cG+c00(2G+c)c−G000(2G+c)c−G00(2G+c)cG+c000000(2G+c)c−G00(2G+c)cG+c000000(2G+c)c−G00(2G+c)cG+c⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
D e ′ : ( c I + D e ′ ) − 1 : D e ′ = [ 4 G 2 2 G + c 0 0 0 0 0 0 0 0 0 4 G 2 2 G + c 0 0 0 0 0 0 0 0 0 4 G 2 2 G + c 0 0 0 0 0 0 0 0 0 2 G 2 ( 2 G + c ) 0 0 2 G 2 ( 2 G + c ) 0 0 0 0 0 0 2 G 2 ( 2 G + c ) 0 0 2 G 2 ( 2 G + c ) 0 0 0 0 0 0 2 G 2 ( 2 G + c ) 0 0 2 G 2 ( 2 G + c ) 0 0 0 2 G 2 ( 2 G + c ) 0 0 2 G 2 ( 2 G + c ) 0 0 0 0 0 0 2 G 2 ( 2 G + c ) 0 0 2 G 2 ( 2 G + c ) 0 0 0 0 0 0 2 G 2 ( 2 G + c ) 0 0 2 G 2 ( 2 G + c ) ] \begin{aligned} &\bm{D'_e}:(c \bm{I}+ \bm{D'_e})^{-1}:\bm{D'_e} =\\\hdashline &\left[\begin{array}{ccc:ccc:ccc} \frac{4G^2}{2G+c} &0&0&0&0&0&0&0&0\\ 0&\frac{4G^2}{2G+c} &0&0&0&0&0&0&0\\ 0&0&\frac{4G^2}{2G+c} &0&0&0&0&0&0\\\hdashline 0 &0&0&\frac{2G^2}{(2G+c)} &0&0&\frac{2G^2}{(2G+c)} &0&0\\ 0&0&0&0&\frac{2G^2}{(2G+c)} &0&0&\frac{2G^2}{(2G+c)} &0\\ 0&0&0&0&0&\frac{2G^2}{(2G+c)} &0&0&\frac{2G^2}{(2G+c)} \\\hdashline 0 &0&0&\frac{2G^2}{(2G+c)} &0&0&\frac{2G^2}{(2G+c)} &0&0\\ 0&0&0&0&\frac{2G^2}{(2G+c)} &0&0&\frac{2G^2}{(2G+c)} &0\\ 0&0&0&0&0&\frac{2G^2}{(2G+c)} &0&0&\frac{2G^2}{(2G+c)} \\ \end{array}\right] \end{aligned} De′:(cI+De′)−1:De′=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡2G+c4G20000000002G+c4G20000000002G+c4G2000000000(2G+c)2G200(2G+c)2G2000000(2G+c)2G200(2G+c)2G2000000(2G+c)2G200(2G+c)2G2000(2G+c)2G200(2G+c)2G2000000(2G+c)2G200(2G+c)2G2000000(2G+c)2G200(2G+c)2G2⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
D e ′ − D e ′ : ( c I + D e ′ ) − 1 : D e ′ = [ 2 G c 2 G + c 0 0 0 0 0 0 0 0 0 2 G c 2 G + c 0 0 0 0 0 0 0 0 0 2 G c 2 G + c 0 0 0 0 0 0 0 0 0 G c ( 2 G + c ) 0 0 G c ( 2 G + c ) 0 0 0 0 0 0 G c ( 2 G + c ) 0 0 G c ( 2 G + c ) 0 0 0 0 0 0 G c ( 2 G + c ) 0 0 G c ( 2 G + c ) 0 0 0 G c ( 2 G + c ) 0 0 G c ( 2 G + c ) 0 0 0 0 0 0 G c ( 2 G + c ) 0 0 G c ( 2 G + c ) 0 0 0 0 0 0 G c ( 2 G + c ) 0 0 G c ( 2 G + c ) ] \begin{aligned} &\bm{D'_e}-\bm{D'_e}:(c \bm{I}+ \bm{D'_e})^{-1}:\bm{D'_e} =\\\hdashline &\left[\begin{array}{ccc:ccc:ccc} \frac{2Gc}{2G+c} &0&0&0&0&0&0&0&0\\ 0&\frac{2Gc}{2G+c} &0&0&0&0&0&0&0\\ 0&0&\frac{2Gc}{2G+c} &0&0&0&0&0&0\\\hdashline 0 &0&0&\frac{Gc}{(2G+c)} &0&0&\frac{Gc}{(2G+c)} &0&0\\ 0&0&0&0&\frac{Gc}{(2G+c)} &0&0&\frac{Gc}{(2G+c)} &0\\ 0&0&0&0&0&\frac{Gc}{(2G+c)} &0&0&\frac{Gc}{(2G+c)} \\\hdashline 0 &0&0&\frac{Gc}{(2G+c)} &0&0&\frac{Gc}{(2G+c)} &0&0\\ 0&0&0&0&\frac{Gc}{(2G+c)} &0&0&\frac{Gc}{(2G+c)} &0\\ 0&0&0&0&0&\frac{Gc}{(2G+c)} &0&0&\frac{Gc}{(2G+c)} \\ \end{array}\right] \end{aligned} De′−De′:(cI+De′)−1:De′=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡2G+c2Gc0000000002G+c2Gc0000000002G+c2Gc000000000(2G+c)Gc00(2G+c)Gc000000(2G+c)Gc00(2G+c)Gc000000(2G+c)Gc00(2G+c)Gc000(2G+c)Gc00(2G+c)Gc000000(2G+c)Gc00(2G+c)Gc000000(2G+c)Gc00(2G+c)Gc⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
[ D e ′ − D e ′ : ( c I + D e ′ ) − 1 : D e ′ ] : ( I − 1 3 I ^ ) + K I ^ = [ K + 4 G c 3 ( 2 G + c ) K + − 2 G c 3 ( 2 G + c ) K + − 2 G c 3 ( 2 G + c ) 0 0 0 0 0 0 K + − 2 G c 3 ( 2 G + c ) K + 4 G c 3 ( 2 G + c ) K + − 2 G c 3 ( 2 G + c ) 0 0 0 0 0 0 K + − 2 G c 3 ( 2 G + c ) K + − 2 G c 3 ( 2 G + c ) K + 4 G c 3 ( 2 G + c ) 0 0 0 0 0 0 0 0 0 G c ( 2 G + c ) 0 0 G c ( 2 G + c ) 0 0 0 0 0 0 G c ( 2 G + c ) 0 0 G c ( 2 G + c ) 0 0 0 0 0 0 G c ( 2 G + c ) 0 0 G c ( 2 G + c ) 0 0 0 G c ( 2 G + c ) 0 0 G c ( 2 G + c ) 0 0 0 0 0 0 G c ( 2 G + c ) 0 0 G c ( 2 G + c ) 0 0 0 0 0 0 G c ( 2 G + c ) 0 0 G c ( 2 G + c ) ] \begin{aligned} &\left[\bm{D'_e}-\bm{D'_e}:(c \bm{I}+ \bm{D'_e})^{-1}:\bm{D'_e}\right]:(\bm{I-\frac{1}{3}{\hat{I}}})+K\bm{\hat{I}}=\\\hdashline &\left[ \begin{array}{ccc:ccc:ccc} K+\frac{4Gc}{3(2G+c)} &K+\frac{-2Gc}{3(2G+c)} &K+\frac{-2Gc}{3(2G+c)} &0&0&0&0&0&0\\ K+\frac{-2Gc}{3(2G+c)} &K+\frac{4Gc}{3(2G+c)} &K+\frac{-2Gc}{3(2G+c)} &0&0&0&0&0&0\\ K+\frac{-2Gc}{3(2G+c)} &K+\frac{-2Gc}{3(2G+c)} &K+\frac{4Gc}{3(2G+c)} &0&0&0&0&0&0\\\hdashline 0 &0&0&\frac{Gc}{(2G+c)} &0&0&\frac{Gc}{(2G+c)} &0&0\\ 0&0&0&0&\frac{Gc}{(2G+c)} &0&0&\frac{Gc}{(2G+c)} &0\\ 0&0&0&0&0&\frac{Gc}{(2G+c)} &0&0&\frac{Gc}{(2G+c)} \\\hdashline 0 &0&0&\frac{Gc}{(2G+c)} &0&0&\frac{Gc}{(2G+c)} &0&0\\ 0&0&0&0&\frac{Gc}{(2G+c)} &0&0&\frac{Gc}{(2G+c)} &0\\ 0&0&0&0&0&\frac{Gc}{(2G+c)} &0&0&\frac{Gc}{(2G+c)} \\ \end{array}\right] \end{aligned} [De′−De′:(cI+De′)−1:De′]:(I−31I^)+KI^=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡K+3(2G+c)4GcK+3(2G+c)−2GcK+3(2G+c)−2Gc000000K+3(2G+c)−2GcK+3(2G+c)4GcK+3(2G+c)−2Gc000000K+3(2G+c)−2GcK+3(2G+c)−2GcK+3(2G+c)4Gc000000000(2G+c)Gc00(2G+c)Gc000000(2G+c)Gc00(2G+c)Gc000000(2G+c)Gc00(2G+c)Gc000(2G+c)Gc00(2G+c)Gc000000(2G+c)Gc00(2G+c)Gc000000(2G+c)Gc00(2G+c)Gc⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
Voigt表记下的一致刚度矩阵(注:应变为工程应变 γ x y = 2 ε x y γ_{xy}=2ε_{xy} γxy=2εxy):
[ K + 4 G c 3 ( 2 G + c ) K + − 2 G c 3 ( 2 G + c ) K + − 2 G c 3 ( 2 G + c ) 0 0 0 K + − 2 G c 3 ( 2 G + c ) K + 4 G c 3 ( 2 G + c ) K + − 2 G c 3 ( 2 G + c ) 0 0 0 K + − 2 G c 3 ( 2 G + c ) K + − 2 G c 3 ( 2 G + c ) K + 4 G c 3 ( 2 G + c ) 0 0 0 0 0 0 G c ( 2 G + c ) 0 0 0 0 0 0 G c ( 2 G + c ) 0 0 0 0 0 0 G c ( 2 G + c ) ] \left[ \begin{array}{ccc:ccc} K+\frac{4Gc}{3(2G+c)} &K+\frac{-2Gc}{3(2G+c)} &K+\frac{-2Gc}{3(2G+c)} &0&0&0\\ K+\frac{-2Gc}{3(2G+c)} &K+\frac{4Gc}{3(2G+c)} &K+\frac{-2Gc}{3(2G+c)} &0&0&0\\ K+\frac{-2Gc}{3(2G+c)} &K+\frac{-2Gc}{3(2G+c)} &K+\frac{4Gc}{3(2G+c)} &0&0&0\\\hdashline 0 &0&0&\frac{Gc}{(2G+c)} &0&0\\ 0&0&0&0&\frac{Gc}{(2G+c)} &0\\ 0&0&0&0&0&\frac{Gc}{(2G+c)} \\ \end{array}\right] ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡K+3(2G+c)4GcK+3(2G+c)−2GcK+3(2G+c)−2Gc000K+3(2G+c)−2GcK+3(2G+c)4GcK+3(2G+c)−2Gc000K+3(2G+c)−2GcK+3(2G+c)−2GcK+3(2G+c)4Gc000000(2G+c)Gc000000(2G+c)Gc000000(2G+c)Gc⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
umat 程序
SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD,
1 RPL,DDSDDT,DRPLDE,DRPLDT,
2 STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME,
3 NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT,
4 CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,JSTEP,KINC)
C
INCLUDE 'ABA_PARAM.INC'
C
CHARACTER*80 CMNAME
DIMENSION STRESS(NTENS),STATEV(NSTATV),
1 DDSDDE(NTENS,NTENS),DDSDDT(NTENS),DRPLDE(NTENS),
2 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1),
3 PROPS(NPROPS),COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3),
4 JSTEP(4),STRESS_TR(NTENS),STRESS_VALID(NTENS),DSTRAN_P(NTENS)
real LMD
EE=PROPS(1) !modulus
EMU=PROPS(2) !Possion's ritio
SGM_Y=PROPS(3) !yield stress
EC=PROPS(4) !hardening
LMD=EE*EMU/((1.0+EMU)*(1.0-2.0*EMU))
EG=EE/(2.0*(1.0+EMU))
EK=EE/(3.0*(1.0-2.0*EMU))
DDSDDE=0.0
DO I=1,NDI
DDSDDE(I,I)=2*EG
ENDDO
DO I=NDI+1,NTENS
DDSDDE(I,I)=EG
ENDDO
DO I=1,NDI
DO J=1,NDI
DDSDDE(I,J)=DDSDDE(I,J)+LMD
ENDDO
ENDDO
DO I=1,NTENS
STRESS_TR(I)=STRESS(I)
ENDDO
DO I=1,NTENS
DO J=1,NTENS
STRESS_TR(I)=STRESS_TR(I)+ DDSDDE(I,J)*DSTRAN(J)
ENDDO
ENDDO
C 计算有效屈服应力
C STATEV(1) ~ STATEV(NTENS) 为背应力
DO I=1,NTENS
STRESS_VALID(I)=STRESS_TR(I)-STATEV(I)
ENDDO
STRESS_V=0.0
DO I=1,NDI
STRESS_V=STRESS_V+STRESS_VALID(I)
ENDDO
STRESS_V=STRESS_V/3.0
STRESS_MISES=0.0
DO I=1,NDI
STRESS_MISES=STRESS_MISES+(STRESS_VALID(I)-STRESS_V)**2.0
ENDDO
DO I=1+NDI,NTENS
STRESS_MISES=STRESS_MISES+2.0*STRESS_VALID(I)**2.0
ENDDO
STRESS_MISES=SQRT(1.5*STRESS_MISES)
C 判断是否屈服
IF (STRESS_MISES .LE. SGM_Y) THEN
DO I=1,NTENS
STRESS(I)=STRESS_TR(I)
ENDDO
ELSE !屈服
DP=(STRESS_MISES-SGM_Y)/(EC+3.0*EG)
DO I=1,NDI
DSTRAN_P(I)=DP*1.5*(STRESS_VALID(I)-STRESS_V)/STRESS_MISES
ENDDO
DO I=1+NDI,NTENS
DSTRAN_P(I)=DP*1.5*STRESS_VALID(I)/STRESS_MISES
ENDDO
DO I=1,NTENS !应力更新
DO J=1,NTENS
STRESS(I)=STRESS(I)+ DDSDDE(I,J)*(DSTRAN(J)-DSTRAN_P(J))
ENDDO
ENDDO
DO I=1,NTENS !背应力更新
STATEV(I)=STATEV(I)+DSTRAN_P(I)*EC
ENDDO
ENDIF
RETURN
END