编码踩坑——MySQL order by&limit顺序不一致 / 堆排序 / 排序稳定性
本篇介绍一个MySQL下SQL查询语句同时包含order by和limit出现的一个问题及原因,其中涉及的知识点包括 :MySQL对limit的优化、MySQL的order排序、优先级队列和堆排序、堆排序的不稳定性;
问题现象
后台应用,有个表单查询接口:
允许用户设置页码的pageNum和页数据大小pageSize;pageSize则作为SQL的limit参数;
查询结果根据参数rank排序输出;rank作为SQL的order by参数;
现象:当用户分别输入不同的pageSize时(pageSize=10和pageSize=20),查询返回的结果集中,存在部分元素在先后两次查询中,相对顺序不一致;
原因分析
分析不同limit N下返回的数据,发现顺序不一致的结果集有一个共同特点——顺序不一致的这几条数据,他们用来排序的参数值rank相同;
也就是说,带limit的order by查询,只保证排序值rank不同的结果集的绝对有序,而排序值rank相同的结果不保证顺序;推测MySQL对order by limit进行了优化;limit n, m不需返回全部数据,只需返回前n项或前n + m项;
上面的推测在MySQL官方文档中找到了相关的说明:
If an index is not used for ORDER BY but a LIMIT clause is also present, the optimizer may be able to avoid using a merge file and sort the rows in memory using an in-memory filesort operation. For details, see The In-Memory filesort Algorithm.
解释:在ORDER BY + LIMIT的查询语句中,如果ORDER BY不能使用索引的话,优化器可能会使用in-memory sort操作;
关于排序方法
思考下对于这种排序问题,如果让我们自己处理,会如何做?——其实本质上就是topN的解决方法;回顾一下排序算法,适用于取前n的算法也只有堆排序了;
那么,MySQL会不会也使用了类似的优化方法呢?
参考The In-Memory filesort Algorithm可知MySQL的filesort有3种优化算法,分别是:
基本filesort
改进filesort
In memory filesort
而上面的提到的In memory filesort,官方文档这么说明:
The sort buffer has a size of sort_buffer_size. If the sort elements for N rows are small enough to fit in the sort buffer (M+N rows if M was specified), the server can avoid using a merge file and performs an in-memory sort by treating the sort buffer as a priority queue.
这里提到了一个关键词——优先级队列;而优先级队列的原理就是二叉堆,也就是堆排序;下面简单介绍下堆排序;
堆排序
什么是堆?
堆是一种特殊的树,它满足需要满足两个条件:
(1)堆是一种完全二叉树,也就是除了最后一层,其他层的节点个数都是满的,最后一个节点都靠左排列;
(2)堆中每一个节点的值都必须大于等于(或小于等于)其左右子节点的值;
对于每个节点的值都大于等于子树中每个节点值的堆,叫作“大顶堆”;
对于每个节点的值都小于等于子树中每个节点值的堆,叫作“小顶堆”;
堆的存储?
用数组来存储完全二叉树是非常节省内存空间的,因为我们不需要存储左右子节点的指针,单纯通过数组的下标,就可以找到一个节点的子节点和父节点;
从图中我们可以看到,数组中下标为 i 的节点的左子节点,就是下标为 i∗2 的节点,右子节点就是下标为 i∗2+1的节点,父节点就是下标为i/2的节点;
堆的核心操作
堆尾部插入元素;可用作堆排序的初始化操作,把排序的数组元素按顺序插入堆;
例如:在已经建好的堆中插入值为“22”的结点,这时候就需要重新调整堆结构,过程如下:
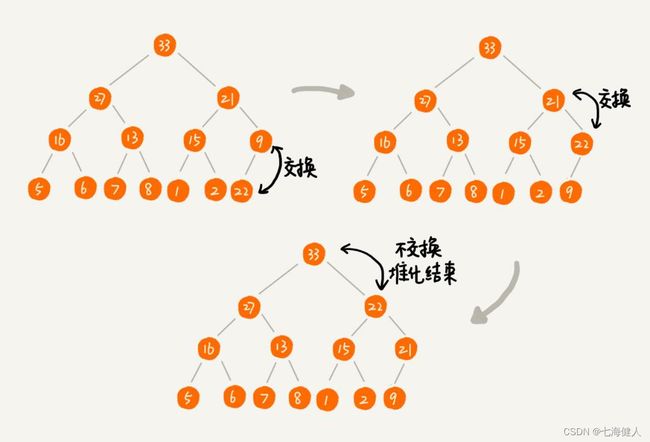
2.堆顶的移出操作;可用作堆排序的取出最大值(大顶堆)操作,把堆尾部元素放到堆顶,从上到下重新做"堆化"操作(对于不满足父子节点大小关系的,互换两个节点,并且重复进行这个过程,直到父子节点之间满足大小关系为止);
例如:删除堆顶的“33”结点,删除步骤如下:
注意这里的一个关键步骤——取出堆顶元素后,堆尾部元素会换到堆顶,重新从上到下的"堆化";这个交换很关键,正是这个交换把原数组越往后的元素给移到了数组的前面,因而可能导致相同值的元素的原始相对位置发生变化;
堆排序
堆排序是指利用堆这种数据结构进行排序的一种算法;
排序过程中,只需要个别临时存储空间,所以堆排序是原地排序算法,空间复杂度为O(1);
堆排序的过程分为建堆和排序两大步骤;建堆过程的时间复杂度为O(n),排序过程的时间复杂度为O(nlogn),所以,堆排序整体的时间复杂度为O(nlogn);
堆排序不是稳定的算法,因为在排序的过程中,每取出一次堆顶元素,都需要将堆的最后一个节点跟堆顶节点互换的操作(也就是上面提到的"堆顶的移出操作"),所以可能把值相同数据中,原本在数组序列后面的元素,通过交换到堆顶,从而改变了这些值相同的元素的原始相对顺序;因此是不稳定的;
——这也就是为什么当改变SQL的limit的大小,返回的排序结果中,相同排序值rank的记录的相对顺序发生变化的根本原因!
堆排序步骤
(1)建堆:建堆结束后,数组中的数据已经是按照大顶堆的特性组织的;数组中的第一个元素就是堆顶;
(2)取出最大值(类似删除操作):将堆顶元素a[1]与最后一个元素a[n]交换,这时,最大元素就放到了下标为n的位置;
(3)重新堆化:交换后新的堆顶可能违反堆的性质,需要重新进行堆化;
(4)重复(2)(3)操作,直到最后堆中只剩下下标为1的元素,排序就完成了;
堆排序相关代码示例(Java)
堆的定义,含堆的存储数组以及当前堆的元素数量,堆的堆尾插入和堆顶移除方法
/**
* 大顶堆
*/
public class Heap {
/**
* 存储堆数据结构的数组,从下标1开始存储数据
*/
Node[] array;
/**
* 堆中已经存储的数据个数 用来判断是否还能继续插入元素;因为从1开始存 因此count也是最后一个数组元素的下标
*/
int count;
public Heap(int nodeNum) {
// 数组下标0不存储 因此数组大小+1
array = new Node[nodeNum + 1];
count = 0;
}
//堆的核心操作-----插入元素和删除元素
/**
* 堆的插入——堆尾插入数据,并从下往上"堆化"
*/
public void insert(Node node) {
// 堆可以存储的最大数据个数为array.length-1(数组下标从1开始)
int maxNum = array.length - 1;
// 插入之前已经堆满了
if (count >= maxNum) {
return;
}
count++;
// 当前节点放入堆尾部
array[count] = node;
// 因为这里是插入数据到堆尾部,这里使用从下往上的方式重新堆化;
int i = count;
// 从插入位置开始 从下往上执行堆化
HeapSortUtils.heapMoveDesc(array, i);
}
/**
* 移出堆顶元素,将最后节点交换到堆顶位置 重新从新插入的位置开始 从上到下执行堆化
*/
public Node removeMax() {
if (count == 0) {
return null;
}
// 取出堆顶元素
final Node maxNode = array[1];
// 将最后节点放入堆顶
array[1] = array[count];
// 元素总数-1
count--;
// 从插入的位置(堆顶——数组下标为1)往下执行堆化
HeapSortUtils.heapMoveAsc(array, count, 1);
return maxNode;
}
}堆节点的定义,这里包含两个属性id和rank,用来说明相同rank原色的原始顺序被改变
/**
* 堆二叉树节点 主键id和排序值rank
*/
public class Node {
public Node(int id, int rank) {
this.id = id;
this.rank = rank;
}
/**
* 记录的唯一id
*/
int id;
/**
* 记录的排序参数
*/
int rank;
@Override
public String toString() {
return "Node{id=" + id + ", rank=" + rank + "}";
}
}堆排序工具类,包含取堆的父/左/右节点方法、交换数组元素、打印数组元素、从下往上执行堆化(用于插入元素)、从上往下执行堆化(用于移除元素或堆初始化)、堆的初始化、堆排序;
import java.util.Arrays;
import java.util.List;
/**
* @author Akira
* @description Heap
* 1. 什么是堆?
* 堆是一种特殊的树,它满足需要满足两个条件:
* (1)堆是一种完全二叉树,也就是除了最后一层,其他层的节点个数都是满的,最后一个节点都靠左排列。
* (2)堆中每一个节点的值都必须大于等于(或小于等于)其左右子节点的值。
* 对于每个节点的值都大于等于子树中每个节点值的堆,我们叫作“大顶堆”。对于每个节点的值都小于等于子树中每个节点值的堆,我们叫作“小顶堆”。
* 2. 怎么存储堆?
* 用数组来存储完全二叉树是非常节省内存空间的,因为我们不需要存储左右子节点的指针,单纯通过数组的下标,就可以找到一个节点的子节点和父节点。
* 数组中下标为 i 的节点的左子节点,就是下标为 i∗2 的节点,右子节点就是下标为 i∗2+1的节点,父节点就是下标为i/2的节点。
* 3. 堆排序步骤?
* (1)先构建堆,按照排序的元素顺序,往堆中插入一个元素;
* (2)依次取出堆顶元素
*/
public class HeapSortUtils {
//-----工具方法
/**
* 判断 数组下标为arrayIndex的节点 是否存在父节点
*/
private static boolean hasParent(int arrayIndex) {
return arrayIndex / 2 > 0;
}
/**
* 判断 数组元素总数为count 数组下标为arrayIndex的节点 是否存在左子节点
*/
private static boolean hasLeft(int arrayIndex, int count) {
return arrayIndex * 2 <= count;
}
/**
* 判断 数组元素总数为count 数组下标为arrayIndex的节点 是否存在右子节点
*/
private static boolean hasRight(int arrayIndex, int count) {
return arrayIndex * 2 + 1 <= count;
}
/**
* 数组元素总数为count 存在父节点时 获取数组下标为arrayIndex的父点
*/
private static Node getParent(Node[] array, int arrayIndex) {
return array[arrayIndex / 2];
}
/**
* 数组元素总数为count 存在左子节点时 获取数组下标为arrayIndex的左子节点
*/
private static Node getLeft(Node[] array, int arrayIndex) {
return array[arrayIndex * 2];
}
/**
* 数组元素总数为count 存在右子节点时 获取数组下标为arrayIndex的右子节点
*/
private static Node getRight(Node[] array, int arrayIndex) {
return array[arrayIndex * 2 + 1];
}
/**
* 交换节点位置 即交换节点的数组下标
*/
static void swap(Node[] array, int i, int j) {
Node temp = array[j];
array[j] = array[i];
array[i] = temp;
}
/**
* 打印
*/
private static void print(Node[] nodeArray, int itemNum) {
for (int i = 1; i < itemNum + 1; i++) {
System.out.println(nodeArray[i]);
}
}
/**
* 核心方法:从数组下标为i的位置,从下往上执行堆化;用于堆元素从堆尾一个个插入,如初始化堆
*/
static void heapMoveDesc(Node[] array, int i) {
// 存在父节点 且 大于父节点,则交换节点
while (hasParent(i) && array[i].rank > getParent(array, i).rank) {
swap(array, i, i / 2);
// 对父节点继续此流程 直到找到堆顶
i = i / 2;
}
}
/**
* 核心方法:从数组下标为i的位置,从上往下执行堆化;用于堆顶元素删除后移动堆尾元素到堆顶
*/
static void heapMoveAsc(Node[] array, int count, int i) {
while (true) {
Node currentNode = array[i];
// 暂存最大值的数组下标(当前节点、左子节点i*2、右子节点i*2+1)
int maxIndex = i;
// 如果左子节点存在 且 左子节点大于当前节点,则把最大数组下标更新为左子节点的数组下标
if (hasLeft(i, count) && currentNode.rank < getLeft(array, i).rank) {
maxIndex = i * 2;
}
// 急需判断 如果右子节点存在 且 由子节点大于当前暂存的maxIndex节点,则把maxIndex更新为右子节点的数组下标
if (hasRight(i, count) && array[maxIndex].rank < getRight(array, i).rank) {
maxIndex = i * 2 + 1;
}
// 如果未发生节点交换(比较完发现最大的还是当前节点)则跳出;否则将当前节点与更大的那个子节点做交换,继续往下比较
if (maxIndex == i) {
break;
}
swap(array, i, maxIndex);
i = maxIndex;
}
}
/**
* 【建堆】就是初始化堆
* 要么:1)从下到上的往堆插入元素,这就需要一个新的空数组来存放堆;
* 要么:2)从后往前处理数组元素,对每个元素执行从上往下堆化;可以直接从最后一个父节点(数组下标为n/2的元素)开始,不用从n开始遍历数组;
*
* @param itemNum
*/
private static Heap buildHeapV1(Node[] nodeArray, int itemNum) {
final Heap heap = new Heap(itemNum);
for (int i = 1; i <= itemNum; i++) {
heap.insert(nodeArray[i]);
}
return heap;
}
private static Heap buildHeapV2(Node[] nodeArray, int itemNum) {
// 第一个父节点的下标
int firstParentIndex = itemNum / 2;
// 从后往前处理数组元素
for (int i = firstParentIndex; i >= 1; i--) {
heapMoveAsc(nodeArray, itemNum, i);
}
// 数组堆化后直接赋值给堆
final Heap heap = new Heap(itemNum);
heap.array = nodeArray;
heap.count = itemNum;
return heap;
}
/**
* 堆排序
* 堆排序的过程分为【建堆】和【排序】两大步骤;建堆过程的时间复杂度为O(n),排序过程的时间复杂度为O(nlogn),所以,堆排序整体的时间复杂度为O(nlogn);
*
* @param nodeArray 存放排序元素的数组
* @param itemNum 元素总数 小于等于nodeArray.length-1
*/
public static void heapSort(Node[] nodeArray, int itemNum) {
// 1.初始化堆 2种方法任选一种都行
final Heap heap = buildHeapV1(nodeArray, itemNum);
final Heap heapV2 = buildHeapV2(nodeArray, itemNum);
// 从堆尾元素开始 从后往前 跟堆顶最大元素做交换
int k = itemNum;
// 依次取出堆中所有堆顶元素 逆序赋值给原数组 完成排序
while (k >= 1) {
final Node maxNode = heapV2.removeMax();
nodeArray[k] = maxNode;
k--;
}
}
/**
* Test
*/
public static void main(String[] args) {
// 初始化排序序列
final List rankList = Arrays.asList(25, 78, 44, 13, 78, 49, 23, 45, 78, 9);
int itemNum = 10;
Node[] array = new Node[itemNum + 1];
for (int i = 1; i < itemNum + 1; i++) {
final Node node = new Node(i, rankList.get(i - 1));
array[i] = node;
}
System.out.println("before sort:");
print(array, itemNum);
// 排序输出
heapSort(array, itemNum);
System.out.println("after sort:");
print(array, itemNum);
}
} 输出:
before sort:
Node{id=1, rank=25}
Node{id=2, rank=78}
Node{id=3, rank=44}
Node{id=4, rank=13}
Node{id=5, rank=78}
Node{id=6, rank=49}
Node{id=7, rank=23}
Node{id=8, rank=45}
Node{id=9, rank=78}
Node{id=10, rank=9}
after sort:
Node{id=10, rank=9}
Node{id=4, rank=13}
Node{id=7, rank=23}
Node{id=1, rank=25}
Node{id=3, rank=44}
Node{id=8, rank=45}
Node{id=6, rank=49}
Node{id=5, rank=78}
Node{id=9, rank=78}
Node{id=2, rank=78}可见,相同rank元素的原始顺序被改变了,堆排序是不稳定的;
小结
现象:SQL查询语句同时包含order by和limit时,当修改limit的值,可能导致"相同排序值的元素之间的现对顺序发生改变"
原因:MySQL对limit的优化,导致当取到指定limit的数量的元素时,就不再继续添加参与排序的记录了,因此参与排序的元素的数量变化了;而MySQL排序使用的In memory filesort是基于优先级队列,也就是堆排序,而堆排序时不稳定的,会改变排序结果中,相同排序值rank的记录的相对顺序;
建议:排序值带上主键id,即order by rank 改为 order by rank, id 即可;
本文参考:
https://zhuanlan.zhihu.com/p/49963490
https://www.cnblogs.com/cjsblog/p/10874938.html
https://blog.csdn.net/qq_55624813/article/details/121316293