Python 无监督学习实用指南：6~10

原文：Hands-on unsupervised learning with Python

协议：CC BY-NC-SA 4.0

译者：飞龙

本文来自【ApacheCN 深度学习 译文集】，采用译后编辑（MTPE）流程来尽可能提升效率。

不要担心自己的形象，只关心如何实现目标。——《原则》，生活原则 2.3.c

六、异常检测

在本章中，我们将讨论无监督学习的实际应用。 我们的目标是训练模型，这些模型要么能够重现特定数据生成过程的概率密度函数，要么能够识别给定的新样本是内部数据还是外部数据。 一般而言，我们可以说，我们要追求的特定目标是发现异常，这些异常通常是在模型下不太可能出现的样本（也就是说，给定概率分布p(x) << λ，其中λ是预定义的阈值），或者离主分布的质心很远。

特别是，本章将包含以下主题：

• 概率密度函数及其基本性质简介
• 直方图及其局限性
• 核密度估计（KDE）
• 带宽选择标准
• 异常检测的单变量示例
• 使用 KDD Cup 99 数据集的 HTTP 攻击异常检测示例
• 单类支持向量机
• 隔离森林的异常检测

技术要求

本章中提供的代码要求：

• Python3.5+（强烈建议使用 Anaconda 发行版）
• 库：
  • SciPy 0.19+
  • NumPy 1.10+
  • Scikit-Learn 0.20+
  • Pandas 0.22+
  • Matplotlib 2.0+
  • Seaborn 0.9+

可以在 GitHub 存储库上找到示例。

概率密度函数

在所有先前的章节中，我们一直认为我们的数据集是从隐式数据生成过程p_data以及所有算法假设x[i] ∈ X为独立同分布的（IID）并进行均匀采样。 我们假设X足够准确地表示p_data，以便算法可以学习使用有限的初始知识进行概括。 相反，在本章中，我们感兴趣的是直接建模p_data，而没有任何具体限制（例如，高斯混合模型通过对数据结构施加约束来实现此目标分布）。 在讨论一些非常有效的方法之前，简要回顾一下在可测量子集X包含于ℜ^n上定义的通用连续概率密度函数p(x)的性质很有帮助（为了避免混淆，我们将用p(x)表示密度函数，用P(x)表示实际概率）：

例如，单变量高斯分布完全由均值μ和方差σ^2来表征：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GbGW0bw5-1681652675127)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/b3f2250c-4a29-4b19-9652-1af23703d1d2.png)]

因此，x ∈ (a, b)的概率如下：

即使连续空间（例如，高斯）中某个事件的绝对概率为零（因为积分具有相同的极值），概率密度函数还是一种非常有用的度量，可以用来将一个样本与另一个对比来了解它。 例如：考虑高斯分布N(0, 1)，密度p(1)= 0.4，而对于x = 2密度降低到大约0.05。 这意味着1的可能性比2高0.4 / 0.05 = 8倍。 同样，我们可以设置可接受阈值α并定义所有x[i]样本，p(x[i]) < α的这些样本为异常（例如，在我们的情况下，α = 0.01）。 这种选择是异常检测过程中的关键步骤，正如我们将要讨论的那样，它还必须包括潜在的异常值，但是这些异常值仍然是常规样本。

在许多情况下，特征向量是使用多维随机变量建模的。 例如：数据集X包含于R^3可以用联合概率密度函数p(x, y, z)表示。 在一般情况下，实际概率需要三重积分：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KE1EJsKK-1681652675128)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/04050c08-87c3-4985-8fa1-45242b98a498.png)]

不难理解，任何使用这种联合概率的算法都会受到复杂性的负面影响。 通过假设单个组件的统计独立性可以大大简化：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5bsdj9x2-1681652675128)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/35903294-84ca-486e-856c-930c74b81e27.png)]

不熟悉此概念的读者可以想象考试前会有大量学生。 用随机变量建模的特征是学习时间（x）和完成课程的数量（y），鉴于这些因素，我们希望找出成功的可能性p(Success | x, y)（此类示例基于条件概率，但主要概念始终相同）。 我们可以假设一个完成所有课程的学生需要在家少学习； 但是，这样的选择意味着两个因素之间的依赖性（和相关性），不能再单独评估了。 相反，我们可以通过假设不存在任何相关性来简化程序，并根据给定的上课次数和作业时间与成功的边际概率进行比较。 重要的是要记住，特征之间的独立性不同于随后从分布中抽取的样本的独立性。 当我们说数据集由 IID 样本组成时，是指概率p(x[i] | x[i-1], x[i-2], ..., p[1]) = p(x[i])。 换句话说，我们假设样本之间没有相关性。 这样的条件更容易实现，因为通常足以洗净数据集以删除任何残余相关性。 取而代之的是，特征之间的相关性是数据生成过程的特殊属性，无法删除。 因此，在某些情况下，我们假定独立性是因为我们知道其影响可以忽略不计，并且最终结果不会受到严重影响，而在其他情况下，我们将基于整个多维特征向量训练模型。 现在，我们可以定义将在其余部分中使用的异常的概念。

作为异常值或新颖性的异常

本章的主题是在没有任何监督的情况下自动检测异常。 由于模型不是基于标记样本提供的反馈，因此我们只能依靠整个数据集的属性来找出相似之处并突出显示不同之处。 特别是，我们从一个非常简单但有效的假设开始：常见事件为正常，而不太可能发生的事件通常被视为异常。 当然，此定义意味着我们正在监视的过程运行正常，并且大多数结果都被认为是有效的。 例如：一家硅加工厂必须将晶圆切成相等的块。 我们知道它们每个都是0.2×0.2英寸（约0.5×0.5厘米），每侧的标准差为 0.001 英寸。 此措施是在 1,000,000 个处理步骤后确定的。 我们是否被授权将0.25×0.25英寸芯片视为异常？ 当然可以。 实际上，我们假设每边的长度都建模为高斯分布（一个非常合理的选择），其中μ = 0.2和σ = 0.001；在经过三个标准差后，概率下降到几乎为零。 因此，例如：P(edge > 0.23)≈ 0，具有这种大小的芯片必须清楚地视为异常。

显然，这是一个非常简单的示例，不需要任何模型。 但是，在现实生活中，密度的结构可能非常复杂，几个高概率区域被低概率区域包围。 这就是为什么必须采用更通用的方法来对整个样本空间进行建模的原因。

当然，异常的语义无法标准化，并且始终取决于所分析的特定问题。 因此，定义异常概念的常见方法是在异常值和新奇之间进行区分。 前者是数据集中包含的样本，即使它们与其他样本之间的距离大于平均值。 因此，离群值检测过程旨在找出此类新奇的样本（例如：考虑之前的示例，如果将0.25×0.25英寸的芯片包含在数据集中，则显然是一个离群值）。 相反，新奇检测的目标略有不同，因为在这种情况下，我们假定使用仅包含正常样本的数据集； 因此，给定一个新的芯片，我们有兴趣了解我们是否可以将其视为来自原始数据生成过程还是离群值（例如：新手技术人员向我们提出以下问题：0.25×0.25英寸的芯片是否是正常芯片）。如果我们已经收集了数据集，则可以使用我们的模型来回答问题。

描述这种情况的另一种方法是将样本视为一系列可能受可变噪声影响的值：y(t) = x(t) + n(t)。 当||n(t)|| << ||x(t)||可以分类为干净：y(t) ≈ x(t)。 相反，当||n(t)|| ≈ ||x(t)||时（或更高），它们是离群值，不能代表真实的基础过程p_data。 由于噪声的平均大小通常比信号小得多，因此P(||n(t)|| ≈ ||x(t)||)的概率接近于零。 因此，我们可以将异常想象为受异常外部噪声影响的正常样本。 异常和噪声样本管理之间真正的主要区别通常在于检测真实异常并相应地标记样本的能力。 实际上，虽然嘈杂的信号肯定已损坏，然后目标是最大程度地减少噪声的影响，但是异常现象可以很容易地被人类识别并正确标记。 但是，正如已经讨论过的，在本章中，我们有兴趣找出不依赖现有标签的发现方法。 此外，为避免混淆，我们总是引用异常，每次定义数据集的内容（仅内部数据或内部数据及异常值）以及我们的分析目标。 在下一部分中，我们将简要讨论数据集的预期结构。

数据集的结构

在标准监督（通常也是非监督）任务中，数据集有望达到平衡。 换句话说，属于每个类别的样本数量应该几乎相同。 相反，在本章要讨论的任务中，我们假设数据集X非常不平衡（包含N个样本）：

• N[outlier] << N，如果存在离群检测（即数据集部分为污垢； 因此找出一种方法将所有异常值过滤掉）
• N[outlier] = 0（或更实际地，P(N[outlier] > 0) → 0，如果存在新颖性检测（也就是说，我们通常可以信任现有样本，而将注意力集中在新样本上）

这些标准的原因很明显：让我们考虑前面讨论的示例。 如果在 1,000,000 个处理步骤后观察到的异常率等于 0.2%，则表示存在 2,000 个异常，这对于一个工作过程而言可能是一个合理的值。 如果这个数字大得多，则意味着系统中应该存在一个更严重的问题，这超出了数据科学家的职责范围。 因此，在这种情况下，我们期望一个数据集包含大量正确的样本和非常少的异常（甚至为零）。 在许多情况下，经验法则是反映潜在的数据生成过程，因此，如果专家可以确认例如发生 0.2% 的异常，则该比率应为1000÷2来找出现实的概率密度函数。 实际上，在这种情况下，更重要的是找出确定异常值可区分性的因素。 另一方面，如果要求我们仅执行新颖性检测（例如：区分有效和恶意网络请求），则必须对数据集进行验证，以便不包含异常，但同时要进行反映负责所有可能有效样本的真实数据生成过程。

实际上，如果正确样本的数量是详尽无遗的，则与高概率区域的任何较大偏差都足以触发警报。 相反，真实数据生成过程的有限区域可能会导致假阳性结果（也就是说，尚未包含在训练集中并被错误标识为异常值的有效样本）。 在最坏的情况下，如果特征发生更改（即，错误地识别为有效样本的离群值），则噪声很大的子集也可能确定假阴性。 但是，在大多数现实生活中，最重要的因素是样本的数量和收集样本的环境。 毋庸置疑，任何模型都必须使用将要测试的相同类型的元素进行训练。 例如：如果使用低精度的仪器在化工厂内部进行测量，则高精度采集的测试可能无法代表总体（当然，它们比数据集可靠得多）。 因此，在进行分析之前，我强烈建议您仔细检查数据的性质，并询问是否所有测试样本均来自同一数据生成过程。

现在，我们可以介绍直方图的概念，这是估计包含观测值的数据集分布的最简单方法。

直方图

找出概率密度函数近似值的最简单方法是基于频率计数。 如果我们有一个包含m样本的数据集x[i] ∈ X（为简单起见，我们仅考虑单变量分布，但是过程对于多维样本完全相同），我们可以如下定义m和M：

间隔(m, M)可以分为固定数量的b个桶（它们可以具有相同或不同的宽度，表示为w(b[j])，因此n[p](b[j])对应于箱b[j]中包含的样本数。此时，给定测试样本x[t]，很容易理解，通过检测包含x[t]的桶可以很容易地获得概率的近似值 ，并使用以下公式：

在分析这种方法的利弊之前，让我们考虑一个简单的示例，该示例基于细分为 10 个不同类别的人群的年龄分布：

import numpy as np

nb_samples = [1000, 800, 500, 380, 280, 150, 120, 100, 50, 30]

ages = []

for n in nb_samples:
    i = np.random.uniform(10, 80, size=2)
    a = np.random.uniform(i[0], i[1], size=n).astype(np.int32)
    ages.append(a)

ages = np.concatenate(ages)

只能使用随机种子1000（即，设置np.random.seed(1000)）来复制数据集。

ages 数组包含所有样本，我们想创建一个直方图以初步了解分布。 我们将使用 NumPy np.histrogram()函数，该函数提供所有必需的工具。 要解决的第一个问题是找出最佳箱数。 对于标准分布，这可能很容易，但是如果没有关于概率密度的先验知识，则变得非常困难。 原因很简单：因为我们需要用一个逐步函数来近似一个连续函数，所以 bin 的宽度决定了最终精度。 例如：如果密度是平坦的（例如：均匀分布），那么几个箱就足以达到良好的效果。 相反，当存在峰时，在函数的一阶导数较大时将更多（较短）的 bin 放在区域中，在导数接近零（表示平坦区域）时将较小的数目放置在区域中会很有帮助。 正如我们将要讨论的，使用更复杂的技术可以使此过程变得更容易，而直方图通常基于对最佳仓数的更粗略计算。 特别是，NumPy 允许设置bins='auto'参数，该参数将强制算法根据明确定义的统计方法（基于 Freedman Diaconis Estimator 和 Sturges 公式）自动选择数字：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nwdpIFPC-1681652675129)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/ad9c7ed6-68a9-47f3-9993-9ed18def14f8.png)]

在上式中，四分位数范围（IQR）对应于第 75^个和第 25^个百分位数。 由于我们对分布没有一个清晰的概念，因此我们希望依靠自动选择，如以下代码片段所示：

import numpy as np

h, e = np.histogram(ages, bins='auto')

print('Histograms counts: {}'.format(h))
print('Bin edges: {}'.format(e))

上一个代码段的输出如下：

Histograms counts: [177  86 122 165 236 266 262 173 269 258 241 116 458 257 311   1   1   5 6]
Bin edges: [16\.         18.73684211 21.47368421 24.21052632 26.94736842 29.68421053
 32.42105263 35.15789474 37.89473684 40.63157895 43.36842105 46.10526316
 48.84210526 51.57894737 54.31578947 57.05263158 59.78947368 62.52631579
 65.26315789 68\.        ]

因此，该算法定义了 19 个 bin，并已输出频率计数和边缘（即，最小值为16，最大值为68）。 现在，我们可以显示直方图的图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rirVoFrE-1681652675129)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/ab4c2cc0-deca-42f2-a783-a8ed3259ff51.png)]

测试分布的直方图

该图证实该分布是非常不规则的，并且一些区域的峰被平坦区域包围。 如前所述，当查询基于样本属于特定区域的概率时，直方图会很有帮助。 例如，在这种情况下，我们可能有兴趣确定某个人的年龄在 48.84 和 51.58 之间（对应于第 12 个桶）的概率从 0 开始）。 由于所有箱的宽度相同，因此我们可以简单地用n[p](b[12])（h[12]）和m（ages.shape[0]）：

d = e[1] - e[0]
p50 = float(h[12]) / float(ages.shape[0])

print('P(48.84 < x < 51.58) = {:.2f} ({:.2f}%)'.format(p50, p50 * 100.0))

输出如下：

P(48.84 < x < 51.58) = 0.13 (13.43%)

因此，概率的近似值约为 13.5%，这也由直方图的结构证实。 但是，读者应该清楚地了解到这种方法有明显的局限性。 首先，也是最明显的是关于箱的数量和宽度。 实际上，一小部分产生的粗略结果无法考虑快速振荡。 另一方面，非常大的数量会产生带孔的直方图，因为大多数桶都没有样本。 因此，考虑到现实生活中可能遇到的所有动态因素，需要一种更可靠的方法。 这是我们将在下一节中讨论的内容。

核密度估计（KDE）

直方图不连续性问题的解决方案可以通过一种简单的方法有效地解决。 给定样本x[i] ∈ X，假设我们使用的是中心为x[i]多元分布，则可以考虑超体积（通常是超立方体或超球体）。 通过一个称为带宽的常数h定义了这样一个区域的扩展（已选择名称以支持该值为正的有限区域的含义）。 但是，我们现在不只是简单地计算属于超体积的样本数量，而是使用具有一些重要特征的平滑核函数K(x[i]; h)来近似估计该值：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zAqSsgwV-1681652675130)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/623f8390-126c-4574-a155-21296102eb0d.png)]

此外，出于统计和实际原因，还必须强制执行以下整数约束（为简单起见，仅在单变量情况下显示，但扩展很简单）：

在讨论称为核密度估计（KDE）的技术之前，显示K(·)的一些常见选择将很有帮助。

高斯核

这是最常用的内核之一，其结构如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LNMNB3YN-1681652675130)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/96057fde-dc28-4cce-945a-c791662917e2.png)]

以下屏幕截图显示了图形表示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zz6t4lY5-1681652675130)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/8f5b2bb9-40c8-42f2-a728-cdf8638c4e33.png)]

高斯核

鉴于其规律性，高斯核是许多密度估计任务的常见选择。 但是，由于该方法不允许混合不同的内核，因此选择时必须考虑所有属性。 从统计数据中，我们知道高斯分布可被视为峰度的平均参考值（峰度与峰高和尾巴的重量成正比）。 为了最大化内核的选择性，我们需要减少带宽。 这意味着即使最小的振荡也会改变密度，并且结果是非常不规则的估计。 另一方面，当h大时（即高斯的方差），近似变得非常平滑，并且可能失去捕获所有峰的能力。 因此，结合选择最合适的带宽，考虑其他可以自然简化流程的内核也会很有帮助。

Epanechnikov 核

已经提出该内核以最小化均方误差，并且它还具有非常规则的性质（实际上，可以想象为倒抛物线）。 计算公式如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-A4qQhiCJ-1681652675131)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/802044f2-601f-4896-b783-f68372d52094.png)]

引入常数ε可以使内核规范化并满足所有要求（以类似的方式，可以在范围内扩展内核(-h, h)，以便与其他函数更加一致）。 以下屏幕截图显示了图形表示：

Epanechnikov 核

当h → 0时，内核会变得非常尖峰。但是，由于其数学结构，它将始终保持非常规则； 因此，在大多数情况下，无需用它代替高斯核（即使后者的均方误差稍大）。 此外，由于函数在x = ±h（对于|x| > h，K(x; h) = 0）不连续，因此可能会导密集度估计值迅速下降，特别是在边界处，例如高斯函数非常缓慢地下降。

指数核

指数核是一个非常高峰的内核，其通用表达式如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dEJcl60l-1681652675131)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/00116f24-e19c-42be-b5cd-868d44bcd7c3.png)]

与高斯核相反，该核的尾巴很重，峰尖尖。 以下屏幕截图显示了一个图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FuJ50puX-1681652675136)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/ec0ecff9-d103-47f7-ae02-f4c43a4192cf.png)]

指数核

可以看到，这样的函数适合于建模非常不规则的分布，其密度高度集中在某些特定点周围。 另一方面，当数据生成过程非常规则且表面光滑时，误差可能会非常高。 平均积分平方误差（MISE）可以用来评估内核（和带宽）的表现，是一种很好的理论方法，其定义如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-f7oB2vWE-1681652675136)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/2f177691-5433-440d-b548-5620efa7b7af.png)]

在上一个公式中，p[K](x)是估计的密度，而p(x)是实际的密度。 不幸的是，p(x)是未知的（否则，我们不需要任何估计）。 因此，这种方法只能用于理论评估（例如：Epanechnikov 核的最优性）。 但是，很容易理解，只要内核无法保持接近实际表面，MISE 就会更大。 由于指数突然跃升至峰值，因此仅在特定情况下才适用。 在所有其他情况下，它的行为会导致更大的 MISE，因此最好使用其他内核。

均匀（或 Tophat）内核

这是最简单且不太平滑的内核函数，其用法类似于构建直方图的标准过程。 它等于以下内容：

显然，这是一个在带宽界定的范围内恒定的步骤，仅在估计不需要平滑时才有用。

估计密度

一旦选择了核函数，就可以使用 k 最近邻方法建立概率密度函数的完全近似值。 实际上，给定数据集X（为简单起见，X ∈ R^m，所以这些值是实数），例如，通过创建球形树，很容易（如第 2 章，“聚类基础知识”中所述）以有效的方式对数据进行分区。 当数据结构准备就绪时，可以在带宽定义的半径范围内获得查询点x[j]的所有邻居。 假设这样的集合是X[j] = {x[1], ..., x[t]}，点数是N[j]。 概率密度的估计如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Bae1MZgy-1681652675137)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/93a535f7-f555-4e22-b5da-bed6fa8503ba.png)]

不难证明，如果适当地选择了带宽（根据邻域中包含的样本数量而定），p[K]的概率就会收敛到实际的p(x)。 换句话说，如果粒度足够大，则近似值与真实密度之间的绝对误差将收敛为零。 下图显示了p[K](x[j])的构建过程：

x[j]的密度估计。 在属于x[j]邻域的每个点中评估内核函数

在这一点上，自然会问为什么不为每个查询使用整个数据集而不是 KNN 方法？ 答案很简单，它基于这样的假设：可以使用局部行为轻松地插值以x[j]计算的密度函数的值（即，对于多变量分布，以x[j]为中心的球和远点对估计没有影响。 因此，我们可以将计算限制为X的较小子集，避免包含接近零的贡献。

在讨论如何确定最佳带宽之前，让我们展示一下先前定义的数据集的密度估计（使用 scikit-learn）。 由于我们没有任何特定的先验知识，因此我们将使用具有不同带宽（0.1、0.5 和 1.5）的高斯核。 所有其他参数均保留为其默认值。 但是，KernelDensity类允许设置度量（默认为metric='euclidean'），数据结构（默认为algorithm='auto'，它根据维度在球树和 kd 树之间执行自动选择），以及绝对公差和相对公差（分别为 0 和10^(-8)）。 在许多情况下，无需更改默认值。 但是，对于具有特定特征的超大型数据集，例如，更改leaf_size参数以提高性能可能会有所帮助（如第 2 章，“聚类基础知识”中讨论的 ）。 此外，默认度量标准不能满足所有任务的要求（例如：标准文档显示了一个基于 Haversine 距离的示例，在使用纬度和经度时可以使用该示例）。 在其他情况下，最好使用超立方体而不是球（曼哈顿距离的情况就是这样）。

让我们首先实例化类并拟合模型：

from sklearn.neighbors import KernelDensity

kd_01 = KernelDensity(kernel='gaussian', bandwidth=0.1)
kd_05 = KernelDensity(kernel='gaussian', bandwidth=0.5)
kd_15 = KernelDensity(kernel='gaussian', bandwidth=1.5)

kd_01.fit(ages.reshape(-1, 1))
kd_05.fit(ages.reshape(-1, 1))
kd_15.fit(ages.reshape(-1, 1))

此时，可以调用score_samples()方法来获取一组数据点的对数密度估计值（在我们的示例中，我们正在考虑以 0.05 为增量的范围(10, 70)）。 由于值是log(p)，因此有必要计算exp(log(p))以获得实际概率。

生成的图显示在以下屏幕截图中：

带宽的高斯密度估计：0.1（顶部），0.5（中间）和 1.5（底部）

可能会注意到，当带宽很小（0.1）时，由于缺少特定子范围的样本，因此密度具有强烈的振荡。 当h = 0.5时，轮廓（由于数据集是单变量的）变得更加稳定，但是仍然存在一些由邻居的内部方差引起的残留快速变化。 当h变大（在我们的情况下为 1.5）时，几乎完全消除了这种行为。 一个明显的问题是：如何确定最合适的带宽？ 当然，最自然的选择是使 MISE 最小的h值，但是，正如所讨论的，只有在知道真实的概率密度时才可以使用此方法。 但是，有一些经验标准已经被证实是非常可靠的。 给定完整的数据集X ∈ R^m，第一个数据集基于以下公式：

在我们的案例中，我们获得以下信息：

import numpy as np

N = float(ages.shape[0])
h = 1.06 * np.std(ages) * np.power(N, -0.2)

print('h = {:.3f}'.format(h))

输出如下：

h = 2.415

因此，建议是增加带宽，甚至超过我们上一个实验中的带宽。 因此，第二种方法基于四分位数间距（IQR = Q3-Q1或等效地，第 75 个百分位减去第 25 个百分位），并且对于非常强大的内部变化，它更加健壮：

计算如下：

import numpy as np

IQR = np.percentile(ages, 75) - np.percentile(ages, 25)
h = 0.9 * np.min([np.std(ages), IQR / 1.34]) * np.power(N, -0.2)

print('h = {:.3f}'.format(h))

现在的输出是这样的：

h = 2.051

该值比上一个值小，表明p[K](x)可以使用较小的超体积来更精确。 根据经验，我建议选择带宽最小的方法，即使第二种方法通常在不同情况下也能提供最佳结果。 现在让我们使用h = 2.0以及高斯，Epanechnikov 和指数核（我们将统一的数排除在外，因为最终结果与直方图等效）来重新执行估计：

from sklearn.neighbors import KernelDensity

kd_gaussian = KernelDensity(kernel='gaussian', bandwidth=2.0)
kd_epanechnikov = KernelDensity(kernel='epanechnikov', bandwidth=2.0)
kd_exponential = KernelDensity(kernel='exponential', bandwidth=2.0)

kd_gaussian.fit(ages.reshape(-1, 1))
kd_epanechnikov.fit(ages.reshape(-1, 1))
kd_exponential.fit(ages.reshape(-1, 1))

图形输出显示在以下屏幕截图中：

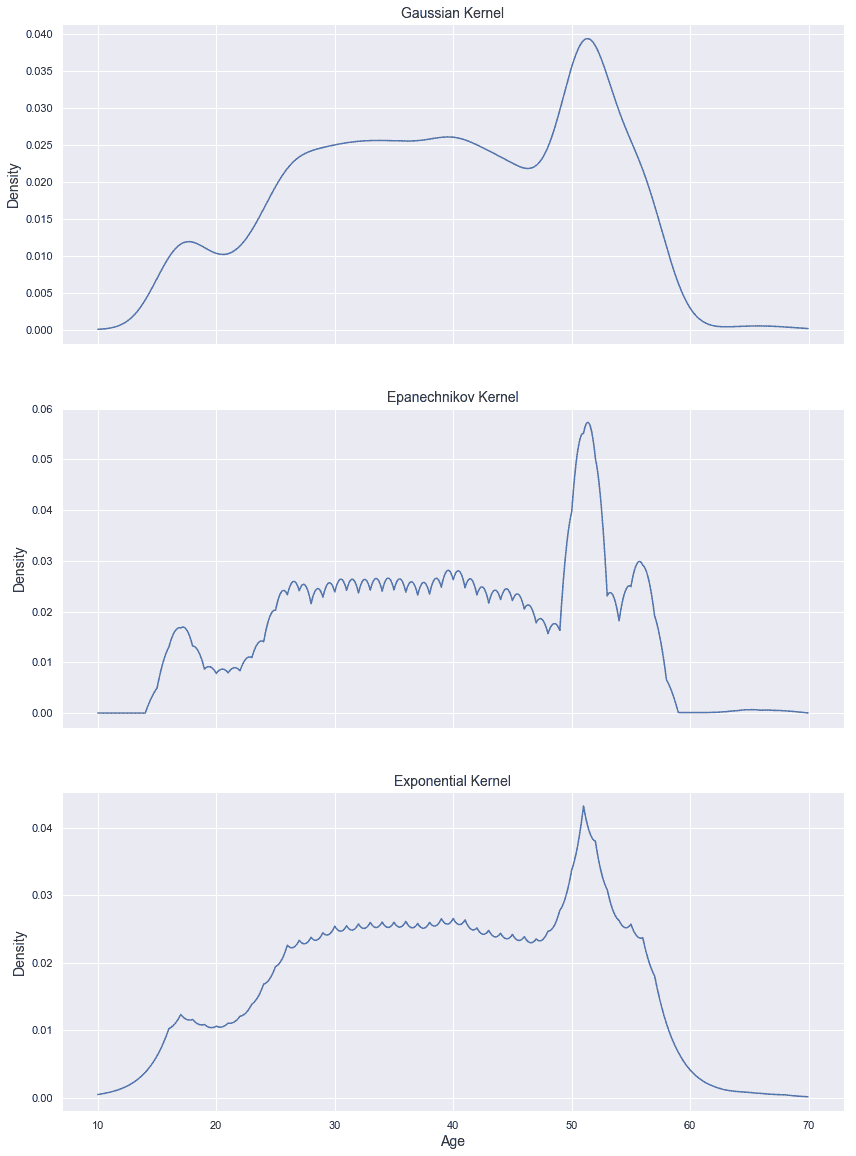
带宽等于 2.0 的密度估计，高斯核（上），Epanechnikov 核（中）和指数核（下）

不出所料，Epanechnikov 和指数核都比高斯核振荡（因为当h较小时，它们倾向于更趋于峰值）； 但是，很明显，中心图肯定是最准确的（就 MISE 而言）。 以前使用高斯核和h = 0.5时已经获得了相似的结果，但是在那种情况下，振荡极为不规则。 如所解释的， Epanechnikov 内核在值达到带宽边界时具有非常强的不连续趋势。 通过查看估计的极端现象可以立即理解该现象，该估计值几乎垂直下降到零。 相反，h = 2的高斯估计似乎非常平滑，并且无法捕获 50 到 60 年之间的变化。 指数核也发生了同样的情况，它也显示出其独特的行为：极端尖刺的极端。 在下面的示例中，我们将使用 Epanechnikov 内核； 但是，我邀请读者也检查带宽不同的高斯过滤器的结果。 这种选择有一个精确的理由（没有充分的理由就不能丢弃）：我们认为数据集是详尽无遗的，并且我们希望对克服自然极端的所有样本进行惩罚。 在所有其他情况下，可以选择非常小的残差概率。 但是，必须考虑每个特定目标做出这样的选择。

异常检测

现在，我们使用 Epanechnikov 密度估计来执行异常检测的示例。 根据概率密度的结构，我们决定在p(x) < 0.005处设置一个截止点。 以下屏幕快照中显示了这种情况：

具有异常截止的 Epanechnikov 密度估计

红点表示将样本归类为异常的年龄限制。 让我们计算一些测试点的概率密度：

import numpy as np

test_data = np.array([12, 15, 18, 20, 25, 30, 40, 50, 55, 60, 65, 70, 75, 80, 85, 90]).reshape(-1, 1)

test_densities_epanechnikov = np.exp(kd_epanechnikov.score_samples(test_data))
test_densities_gaussian = np.exp(kd_gaussian.score_samples(test_data))

for age, density in zip(np.squeeze(test_data), test_densities_epanechnikov):
    print('p(Age = {:d}) = {:.7f} ({})'.format(age, density, 'Anomaly' if density < 0.005 else 'Normal'))

上一个代码片段的输出是这样的：

p(Age = 12) = 0.0000000 (Anomaly)
p(Age = 15) = 0.0049487 (Anomaly)
p(Age = 18) = 0.0131965 (Normal)
p(Age = 20) = 0.0078079 (Normal)
p(Age = 25) = 0.0202346 (Normal)
p(Age = 30) = 0.0238636 (Normal)
p(Age = 40) = 0.0262830 (Normal)
p(Age = 50) = 0.0396169 (Normal)
p(Age = 55) = 0.0249084 (Normal)
p(Age = 60) = 0.0000825 (Anomaly)
p(Age = 65) = 0.0006598 (Anomaly)
p(Age = 70) = 0.0000000 (Anomaly)
p(Age = 75) = 0.0000000 (Anomaly)
p(Age = 80) = 0.0000000 (Anomaly)
p(Age = 85) = 0.0000000 (Anomaly)
p(Age = 90) = 0.0000000 (Anomaly)

可以看到，函数的突然下降造成了某种垂直分离。 年龄15的人几乎处于边界（p(15) ≈ 0.0049），而行为的上限更加剧烈。 截止日期约为 58 年，但年龄60的样本比年龄 57 岁的样本低约 10 倍（这也由初始直方图证实）。 由于这只是一个教学示例，因此很容易检测到异常。 但是，如果没有标准化的算法，即使是稍微更复杂的分布也会产生一些问题。 特别地，在这种简单的单变量分布的特定情况下，异常通常位于尾部。

因此，我们假设给定整体密度估计p[K](x)：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KoLmz3cu-1681652675138)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/749c0092-8f96-4900-8bb3-062de85e7b6a.png)]

当考虑包含所有样本（正常样本和异常样本）的数据集时，这种行为通常是不正确的，并且数据科学家在确定阈值时必须小心。 即使很明显，也最好通过从数据集中删除所有异常来学习正态分布，以展开异常所在的区域（p[K](x) → 0）。 这样，先前的标准仍然有效，并且可以轻松比较不同的密度以进行区分。

在继续下一个示例之前，我建议通过创建人工漏洞并设置不同的检测阈值来修改初始分布。 此外，我邀请读者根据年龄和身高生成双变量分布（例如：基于一些高斯的总和），并创建一个简单的模型，该模型能够检测所有参数不太可能出现的人。

将 KDD Cup 99 数据集用于异常检测

本示例基于 KDD Cup 99 数据集，该数据集收集了一系列正常和恶意的互联网活动。 特别是，我们将重点放在 HTTP 请求的子集上，该子集具有四个属性：持续时间，源字节，目标字节和行为（这是一个分类元素，但是对我们而言，可以立即访问某些特定的属性很有帮助。 攻击）。 由于原始值是非常小的零附近的数字，因此所有版本（包括 scikit-learn 在内）都使用公式log(x + 0.1)（因此，在用新样本模拟异常检测时必须使用它）。 当然，逆变换如下：

让我们首先使用 scikit-learn 内置函数fetch_kddcup99()加载并准备数据集，然后选择percent10=True将数据限制为原始集合的 10% （非常大）。 当然，我邀请读者也使用整个数据集和完整的参数列表（包含 34 个数值）进行测试。

在这种情况下，我们还选择subset='http'，它已经准备好包含大量的正常连接和一些特定的攻击（如在标准期刊日志中）：

from sklearn.datasets import fetch_kddcup99

kddcup99 = fetch_kddcup99(subset='http', percent10=True, random_state=1000)

X = kddcup99['data'].astype(np.float64)
Y = kddcup99['target']

print('Statuses: {}'.format(np.unique(Y)))
print('Normal samples: {}'.format(X[Y == b'normal.'].shape[0]))
print('Anomalies: {}'.format(X[Y != b'normal.'].shape[0]))

输出如下：

Statuses: [b'back.' b'ipsweep.' b'normal.' b'phf.' b'satan.'] Normal samples: 56516 Anomalies: 2209

因此，使用2209恶意样本和56516正常连接有四种类型的攻击（在此情况下，其详细信息不重要）。 为了进行密度估计，为了进行一些初步考虑，我们将把这三个分量视为独立的随机变量（虽然不完全正确，但是可以作为一个合理的起点），但是最终估计是基于完整的联合分布 。 当我们要确定最佳带宽时，让我们执行基本的统计分析：

import numpy as np

means = np.mean(X, axis=0)
stds = np.std(X, axis=0)
IQRs = np.percentile(X, 75, axis=0) - np.percentile(X, 25, axis=0)

上一个代码段的输出如下：

Means: [-2.26381954  5.73573107  7.53879208]
Standard devations: [0.49261436 1.06024947 1.32979463]
IQRs: [0\.         0.34871118 1.99673381]

持续时间的 IQR（第一个部分）为空； 因此，大多数值是相等的。 让我们绘制一个直方图来确认这一点：

第一部分的直方图（持续时间）

不出所料，这种成分不是很重要，因为只有一小部分样本具有不同的值。 因此，在此示例中，我们将跳过它，仅使用源字节和目标字节。 现在，如前所述，计算带宽：

import numpy as np

N = float(X.shape[0])

h0 = 0.9 * np.min([stds[0], IQRs[0] / 1.34]) * np.power(N, -0.2)
h1 = 0.9 * np.min([stds[1], IQRs[1] / 1.34]) * np.power(N, -0.2)
h2 = 0.9 * np.min([stds[2], IQRs[2] / 1.34]) * np.power(N, -0.2)

print('h0 = {:.3f}, h1 = {:.3f}, h2 = {:.3f}'.format(h0, h1, h2))

输出如下：

h0 = 0.000, h1 = 0.026, h2 = 0.133

除了第一个值，我们需要在h1和h2之间进行选择。 由于值的大小不大并且我们希望具有较高的选择性，因此我们将设置h = 0.025，并使用高斯核，该核提供了良好的平滑度。 下面的屏幕快照显示了分割输出（使用包含一个内部 KDE 模块的 seaborn 可视化库获得），其中还包含第一个组件。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-129AhkA6-1681652675139)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/99fdb6a4-0ddc-48d4-8396-53b95f4be661.png)]

正常连接（上面一行）和恶意攻击（下面一行）的密度估计

第一行显示了正常连接的密度，而下一行是恶意攻击。 正如预期的那样，两种情况下的第一部分（持续时间）几乎相同，可以将其丢弃。 相反，源字节和目标字节都表现出非常不同的行为。 在不考虑对数变换的情况下，普通连接平均发送 5 个字节，其方差很小，从而将电位范围扩展到间隔（ 4 ， 6 ） 。 响应具有较大的方差，其值在 4 和 10 之间，并且从 10 开始具有非常低的密度。 相反，恶意攻击的源字节和目标字节都具有两个峰值：一个较短的峰值对应于 -2 ，一个较高的峰值分别对应于大约 11 和。 9 （与正常区域的重叠最小）。 即使不考虑全部联合概率密度，也不难理解大多数攻击会发送更多的输入数据并获得更长的响应（而连接持续时间并没有受到很大影响）。

现在，我们可以通过仅选择正常样本（即，对应于Y == b'normal.'）来训练估计器：

from sklearn.neighbors import KernelDensity

X = X[:, 1:]

kd = KernelDensity(kernel='gaussian', bandwidth=0.025)
kd.fit(X[Y == b'normal.'])

让我们计算正常样本和异常样本的密度：

Yn = np.exp(kd.score_samples(X[Y == b'normal.']))
Ya = np.exp(kd.score_samples(X[Y != b'normal.']))

print('Mean normal: {:.5f} - Std: {:.5f}'.format(np.mean(Yn), np.std(Yn)))
print('Mean anomalies: {:.5f} - Std: {:.5f}'.format(np.mean(Ya), np.std(Ya)))

输出如下：

Mean normal: 0.39588 - Std: 0.25755
Mean anomalies: 0.00008 - Std: 0.00374

显然，当例如p[K](x) < 0.05（考虑三个标准差），我们得到p时，我们可以预期到异常。 [K] (x) ∈ (0, 0.01)，而Yn的中位数约为 0.35。 这意味着至少一半的样本具有p[K](x) > 0.35。 但是，通过简单的计数检查，我们得到以下信息：

print(np.sum(Yn < 0.05))
print(np.sum(Yn < 0.03))
print(np.sum(Yn < 0.02))
print(np.sum(Yn < 0.015))

输出如下：

3147
1778
1037
702

由于有 56,516 个正常样本，我们可以决定选择两个阈值（还要考虑异常离群值）：

• 正常连接：p[K](x) > 0.03
• 中度警报：0.03（涉及 3.1% 的正常样本，可以将其识别为假阳性）
• 高警报：0.015（在这种情况下，只有 1.2% 的正常样本可以触发警报）

此外，在第二个警报中，我们捕获到以下内容：

print(np.sum(Ya < 0.015))

输出如下：

2208

因此，只有一个异常样本具有p[K](x) > 0.015（有 2,209 个向量），这证实了这种选择是合理的。 密度的直方图也证实了先前的结果：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pnK4OMiK-1681652675139)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/646b8603-c9d0-4176-81a6-8ce4046caf50.png)]

异常（左）和正常（右）密度的直方图

正态分布的右尾并不令人担忧，因为异常高度集中在左侧。 在这一领域，也存在大多数异常，因此也是最严重的。 原因与特定域严格相关（对于不同的请求，输入和输出字节可能非常相似），并且在更稳定的解决方案中，有必要考虑其他参数（例如：完整的 KDD Cup 99 数据集） 。 但是，出于教学目的，我们可以定义一个简单的函数（基于先前定义的阈值），以根据源字节和目标字节的数量（不是对数的）检查连接状态：

import numpy as np

def is_anomaly(kd, source, destination, medium_thr=0.03, high_thr=0.015):
    xs = np.log(source + 0.1)
    xd = np.log(destination + 0.1)
    data = np.array([[xs, xd]])

    density = np.exp(kd.score_samples(data))[0]

    if density >= medium_thr:
        return density, 'Normal connection'
    elif density >= high_thr:
        return density, 'Medium risk'
    else:
        return density, 'High risk'

现在，我们可以使用三个不同的示例来测试该函数：

print('p = {:.2f} - {}'.format(*is_anomaly(kd, 200, 1100)))
print('p = {:.2f} - {}'.format(*is_anomaly(kd, 360, 200)))
print('p = {:.2f} - {}'.format(*is_anomaly(kd, 800, 1800)))

输出如下：

p = 0.30 - Normal connection
p = 0.02 - Medium risk
p = 0.00000 - High risk

对于一般概述，还可以考虑源和目标字节密度的双变量图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lv2EjI1x-1681652675139)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/ce9eb95b-7f88-4a3b-9dc0-0faeb226b0bc.png)]

源和目标字节密度的双变量图

前面的屏幕快照确认，尽管攻击通常涉及大量的输入字节，但响应却与正常的响应非常相似，即使它们占据了该区域的最末端。 作为练习，我邀请读者使用整个 KDD Cup 99 数据集训练模型，并找出最佳阈值以检测非常危险和中等风险的攻击。

单类支持向量机

单类支持向量机（SVM）的概念已由 SchölkopfB，Platt JC，Shawe-Taylor JC，Smola AJ 和 Williamson RC 提出（《估计高维分布的支持》），作为一种将新颖性分类为从真实数据生成过程中抽取的样本或异常值的方法。 让我们从我们要实现的目标开始：找到一个无监督模型，在给定样本x[i]的情况下，可以产生二进制输出y[i]（通常，SVM 的结果是双极性的，分别为 -1 和 +1），因此，如果x[i]属于内部，y[i] = 1，如果x[i]是一个异常值，则y [i] = -1，在上述论文中，假设对构成训练集的大多数内线而言，结果是1。 乍一看，这似乎是一个经典的监督问题。 但是，这不是因为不需要标签数据集。 实际上，给定一个包含m样本的数据集X，x[i] ∈ R^n，模型将使用一个固定的类进行训练，目的是找到一个分离的超平面，该平面使X与原点之间的距离最大化。 首先，让我们考虑一个简单的线性情况，如下图所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-D6FX7Won-1681652675140)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/0b1fe0d8-9c63-476f-85b5-359a89c61f10.png)]

线性单类 SVM 方案：训练集与原点分开，具有最大的边距

训练模型以找出使距原点的距离最大的超平面参数。 超平面一侧的所有样本均应为离群值，输出标签为+1，而其余所有样本均被视为离群值，并且输出标签为-1。 此标准似乎有效，但仅适用于线性可分离的数据集。 标准 SVM 通过将数据集（通过函数$1）投影到特征空间D上来解决此问题，在该特征空间D中，它获得了这样的属性：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YF4P3ApB-1681652675140)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/7fde64b8-0a5e-4248-b156-7ac3ec831820.png)]

特别是，考虑到问题的数学性质，如果选择了内核，则投影在计算上变得轻巧。 换句话说，我们要使用一个具有以下属性的函数：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UOdBZ862-1681652675140)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/a1eb4e9a-d241-42fa-acbf-f655dc9eee26.png)]

投影函数$1的存在保证存在于非常容易获得的条件（称为美世条件）下（即，在实子空间中，内核必须为正半 -定）。 这种选择的原因与解决问题的过程密切相关（更详细的解释可以在《机器学习算法第二版》找到）。 但是，不熟悉 SVM 的读者不必担心，因为我们不会讨论太多的数学细节。 要记住的最重要的一点是，不支持任何内核的通用投影会导致计算复杂性急剧增加（尤其是对于大型数据集）。

K(·, ·)的最常见选择之一是径向基函数（已经在第 3 章，“高级聚类”中进行了分析）：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bcukKIPz-1681652675140)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/24030c03-033f-4e35-b840-0349843b16b6.png)]

另一个有用的内核是多项式：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nctQJPT3-1681652675140)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/ea90279d-b782-41ef-b394-ceb0393c3b50.png)]

在这种情况下，指数c定义多项式函数的次数，该次数与特征空间的维数成正比。 但是，内核及其超参数的选择均取决于上下文，并且没有总有效的通用规则。 因此，对于每个问题，都需要进行初步分析，通常还需要进行网格搜索以做出最适当的选择。 一旦选择了内核，就可以用以下方式表示问题：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fI79Xmcy-1681652675141)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/71e19b2a-13bb-4db9-bfb2-e604dd90de9f.png)]

如果不进行全面讨论（超出本书的讨论范围），我们可以将注意力集中在一些重要元素上。 首先，决策函数如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KXgIxmRf-1681652675141)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/482bfa70-c8ff-46f3-9cd6-5380f0e60c9c.png)]

解决方案中涉及的数学过程使我们可以简化以下表达式，但出于我们的目的，最好保留原始表达式。 如果读者具有监督学习的基础知识，他们可以轻松地理解，权重向量与样本x[i]投影之间的点积，可以确定x[i]相对于超平面的位置。 实际上，如果两个向量之间的角度小于 90°（π / 2），则点积是非负的。 当角度正好为 90°（即向量正交）时，它等于零；而当角度在 90° 至 180° 之间时，它等于负。 下图显示了此过程：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PBTSIw24-1681652675141)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/b17e49a6-e73b-4799-bbb4-75604fb98847.png)]

支持向量机中的决策过程

权向量正交于分离超平面。 样本x[i]被确定为一个正常值，因为点积为正且大于阈值ρ。 相反，x[j]被标记为异常值，因为决策函数的符号为负。 项ξ[i] ≥ 0被称为松弛变量，它们的引入是为了产生异常值和正常值间的更灵活的边界。实际上，如果这些变量都等于零（并且为简单起见，ρ = 1），则优化问题的条件变为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WQYTWrlU-1681652675141)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/5a35ab70-84af-4bd0-aec6-dc88a81ec8ad.png)]

这意味着必须将所有训练样本视为内部值，因此必须选择分隔的超平面，以便所有x[i]都在同一侧。 但是，松弛变量的使用通过定义软边界可以提供更大的灵活性。 每个训练样本都与变量x[i]相关联，当然，问题在于将其最小化。 但是，通过这种技巧，即使继续将其识别为离群值，也可以将一些边界样本放置在超平面的另一侧（足够靠近它）。 要考虑的最后一个元素是此上下文中最重要的元素，并且涉及超参数ν ∈ (0, 1)。 在上述论文中，作者证明，每当ρ ≠ 0时，ν都可以解释为训练样本分数的上限，实际上是离群值。 在本章开始时，我们已经指出，在新颖性检测问题中，数据集必须是干净的。 不幸的是，并非总是如此。 因此，v和松弛变量的联合使用使我们也能够处理包含一小部分离群值的数据集。 就概率而言，如果X是从部分被噪声破坏的数据生成过程中提取的，则ν是在X中发现异常值的概率。

现在，基于一个用元组（年龄，身高）识别的学生数据集分析一个二维示例。 我们将从二元高斯分布中得出 2,000 个内点，并均匀采样 200 个测试点：

import numpy as np

nb_samples = 2000
nb_test_samples = 200

X = np.empty(shape=(nb_samples + nb_test_samples, 2))

X[:nb_samples] = np.random.multivariate_normal([15, 160], np.diag([1.5, 10]), size=nb_samples)
X[nb_samples:, 0] = np.random.uniform(11, 19, size=nb_test_samples)
X[nb_samples:, 1] = np.random.uniform(120, 210, size=nb_test_samples)

由于比例尺不同，因此在训练模型之前最好对数据集进行标准化：

from sklearn.preprocessing import StandardScaler

ss = StandardScaler()
Xs = ss.fit_transform(X)

以下屏幕快照显示了标准化数据集的图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-z1od4Pvs-1681652675142)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/0f2a66e7-beca-4734-ac68-5aa079d91c2c.png)]

单类 SVM 示例的数据集

主斑点主要由内部像素组成，一部分测试样本位于同一高密度区域。 因此，我们可以合理地假设在包含所有样本的数据集中有大约 20% 的异常值（因此ν = 0.2）。 当然，这种选择是基于我们的假设，在任何实际场景中， ν的值必须始终反映数据集中预期异常值的实际百分比 。 当此信息不可用时，最好从较大的值开始（例如ν = 0.5），然后再减小它直到找到最佳配置为止（即 ，则错误分类的可能性最小）。

同样重要的是要记住，训练过程有时会找到次优的解决方案。 因此，可以将一些孤立点标记为孤立点。 在这些情况下，最佳策略是测试不同内核的效果，例如，在处理多项式内核时，增加它们的复杂度，直到找到最佳解决方案（不一定排除所有错误）为止。

现在让我们使用 RBF 内核（特别适合于高斯数据生成过程）初始化 scikit-learn OneClassSVM类的实例，并训练模型：

from sklearn.svm import OneClassSVM

ocsvm = OneClassSVM(kernel='rbf', gamma='scale', nu=0.2)
Ys = ocsvm.fit_predict(Xs)

我们根据以下公式选择了建议值gamma='scale'：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PDZC3Tsc-1681652675142)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/9f454540-275e-4d62-bf25-1e2fb9f528be.png)]

通常，这样的选择是最好的起点，可以更改（根据结果是否可接受而增加或减少）。 在我们的情况下，由于数据集是二维（n = 2）和归一化的（std(X) = 1），因此γ = 0.5单位方差高斯分布（因此，我们应该期望它是最合适的选择）。 在这一点上，我们可以通过突出显示异常值来绘制结果：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bIebKa2I-1681652675142)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/5095f406-a826-4c47-bc76-30fd5e3efdf1.png)]

分类结果（左）。 测试集中的异常值（右）

从左图可以看出，该模型已成功识别出数据集的较高密度部分，并且还在密集 Blob 的外部区域中将一些样本标记为离群值。 它们对应于二元高斯条件下具有较低概率的值，在我们的情况下，我们假设它们是应过滤掉的噪声样本。 在右图中，可能只看到离群区域，这当然是高密度斑点的补充。 我们可以得出结论，即使是一类 SVM，即使有点倾向于过拟合，它也可以帮助我们以极小的错误概率识别新颖性。 这也是由于数据集的结构（但是，在许多情况下很常见），可以使用 RBF 内核轻松地对其进行管理。 不幸的是，对于高维数据，通常会丢失这种简单性，并且必须进行更彻底的超参数搜索才能使错误率最小化。

隔离森林的异常检测

Liu FT，Ting KM 和 Zhou Z 在文章《隔离森林》中提出了一种非常强大的异常检测方法。 它基于集成学习的总体框架。 由于该主题范围很广，并且主要涵盖在有监督的机器学习书籍中，因此，如果有必要，我们邀请读者检查建议的资源之一。 相反，在这种情况下，我们将在不非常强力引用所有基础理论的情况下描述模型。

首先，我们说森林是一组称为决策树的独立模型。 顾名思义，它们比算法更实用，是对数据集进行分区的一种实用方法。 从根开始，为每个节点选择一个特征和一个阈值，并将样本分为两个子集（非二叉树不是这样，但是通常，所有涉及的树都是这些模型都是二叉树），如下图所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RMEgqnDe-1681652675143)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/e2cec22b-e13b-4cb0-a353-000c8a4ba3b4.png)]

二叉决策树的通用结构

在有监督的任务中，选择元组（特征，阈值）是根据使子项的杂质最小化的特定标准选择的。 这意味着目标通常是拆分节点，以使结果子集包含属于单个类的大多数样本。 当然，很容易理解，当所有叶子都是纯净的或达到最大深度时，该过程结束。 相反，在此特定上下文中，我们从一个非常特殊（但经过经验证明）的假设开始：如果属于隔离森林的树木每次都选择随机特征和随机阈值进行生长，则从根到包含任何异常值的叶子的路径的平均长度，比隔离异常值所需的路径更长。 通过考虑一个二维示例，可以很容易地理解这一假设的原因，如作者所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KeXnWmbx-1681652675143)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/7b91e898-5147-47c5-b273-a25e89bfe857.png)]

二维随机分区。 在左侧，孤立了一个内部。 在右侧，检测到属于低密度区域的异常值

可以观察到，正常值通常属于高密度区域，需要更多的分区来隔离样本。 相反，由于所需的粒度与斑点的密度成比例，因此可以使用较少的划分步骤来检测低密度区域中的异常值。 因此，建立了一个隔离森林，其目的是测量所有内部节点的平均路径长度，并将其与新样本所需的平均路径长度进行比较。 当这样的长度较短时，成为异常值的可能性增加。 作者提出的异常分数基于指数函数：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uJMd6V8G-1681652675143)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/63000df1-9ce2-4ed6-910d-da875a7cb63b.png)]

在上一个公式中，m是属于训练集X的样本数，avg(h(x[i]))是考虑所有树的x[i]的平均路径长度，c(m)是仅取决于m的规范化项。 当s(x[i], m) → 1时，样本x[i]被识别为异常。 因此，由于s(·)的界限介于 0 和 1 之间，如果我们将阈值设为 0.5，则正常样本与s(x[i], m）<< 0.5。

现在让我们考虑一下葡萄酒数据集，其中包含 178 个样本x[i] ∈ ℜ^13，其中每个特征都是特定的化学性质（例如，酒精，苹果酸，灰分等），并训练一个隔离森林来检测一种新葡萄酒是否可以被认为是一种正常值（例如，现有品牌的变体）还是异常值，因为它的化学特性与每种现有样本不同。 第一步包括加载和规范化数据集：

import numpy as np

from sklearn.datasets import load_wine
from sklearn.preprocessing import StandardScaler

wine = load_wine()
X = wine['data'].astype(np.float64)

ss = StandardScaler()
X = ss.fit_transform(X)

现在，我们可以实例化IsolationForest类并设置最重要的超参数。 第一个是n_estimators=150，它通知模型训练 150 棵树。 另一个基本参数（类似于一类 SVM 中的v）称为contamination，其值表示训练集中异常值的预期百分比。 当我们信任数据集时，我们选择了等于 0.01（1%）的值来解决数量可忽略不计的奇怪样本的存在。 出于兼容性原因，已插入behaviour='new'参数（请查看官方文档以获取更多信息），并且random_state=1000保证实验的可重复性。 一旦类被初始化，就可以训练模型：

from sklearn.ensemble import IsolationForest

isf = IsolationForest(n_estimators=150, behaviour='new', contamination=0.01, random_state=1000)
Y_pred = isf.fit_predict(X)

print('Outliers in the training set: {}'.format(np.sum(Y_pred == -1)))

上一片段的输出为：

2

因此，隔离森林已成功识别出 178 个内岛中的 176 个。 我们可以接受此结果，但是与往常一样，我建议调整参数以获得与每种特定情况都兼容的模型。 此时，我们可以生成一些嘈杂的样本：

import numpy as np

X_test_1 = np.mean(X) + np.random.normal(0.0, 1.0, size=(50, 13))
X_test_2 = np.mean(X) + np.random.normal(0.0, 2.0, size=(50, 13))
X_test = np.concatenate([X_test_1, X_test_2], axis=0)

测试集分为两个块。 第一个数组X_test_1包含噪声水平相对较低的样本（σ = 1），而第二个数组X_test_2包含更多噪声样本（σ = 2）。 因此，我们期望第一组的异常值较低，而第二组的数量较大。 数组X_test是两个测试集的有序连接。 现在让我们预测状态。 由于这些值是双极性的，我们想将它们与训练结果区分开，因此我们将乘以预测时间2（即，-1表示训练集中的离群值，1训练集中的离群值， 测试集中的-2异常值，测试集中的2异常值）：

Y_test = isf.predict(X_test) * 2

Xf = np.concatenate([X, X_test], axis=0)
Yf = np.concatenate([Y_pred, Y_test], axis=0)

print(Yf[::-1])

输出如下：

[ 2 2 -2 -2 -2 -2 -2 2 2 2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 2 -2 2 2 -2 -2 -2 2 -2 -2 -2 -2 2 2 -2 -2 -2 -2 -2 -2 2 2 -2 2 -2 2 -2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 -2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 -1 1 1 1 1 1 1 1 1 1 1 -1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]

由于顺序被保留和反转，我们可以看到属于X_test_2（高方差）的大多数样本被归类为异常，而大多数低方差样本被识别为常值。 为了得到进一步的视觉确认，我们可以执行 t-SNE 降维，考虑到最终结果是二维分布，其 Kullback-Leibler 与原始（13 维）的散度最小。 这意味着所得维数的可解释性非常低，并且只能使用该图来理解二维空间的哪些区域更可能被 inlier 占据：

from sklearn.manifold import TSNE

tsne = TSNE(n_components=2, perplexity=5, n_iter=5000, random_state=1000)
X_tsne = tsne.fit_transform(Xf)

下图显示了结果图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ryGLtovL-1681652675143)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/eb3a4c8f-2ebe-4c56-bf96-92427af3c8c2.png)]

用于葡萄酒数据集的新颖性检测的 t-SNE 图

可以看到，许多接近训练离群点的样本本身就是离群点，并且通常，几乎所有远测样本都是离群点。 但是，由于维数的减少，很难得出更多的结论。 但是，我们知道，当噪声足够小时，找到内点的可能性就很大（这是合理的结果）。 作为练习，我请读者检查一下单个化学性质，以及对于每个或每组，找出哪个阈值可以将一个离群值转换为离群值（例如，回答此问题：与训练集兼容的最大酒精含量是多少？）。

总结

在本章中，我们讨论了概率密度函数的性质以及如何将其用于计算实际概率和相对可能性。 我们已经看到了如何创建直方图，这是将值分组到预定义的 bin 中后代表值频率的最简单方法。 由于直方图有一些重要的局限性（它们非常不连续并且很难找到最佳的 bin 大小），我们引入了核密度估计的概念，这是使用平滑函数估计密度的一种稍微复杂的方法。

我们分析了最常见内核（高斯， Epanechnikov，指数和均匀）的属性，以及两种可用于找出每个数据集最佳带宽的经验方法。 使用这种技术，我们试图基于合成数据集解决一个非常简单的单变量问题。 我们分析了 KDD Cup 99 数据集的 HTTP 子集，其中包含几个正常和恶意网络连接的日志记录。 并且我们已经使用 KDE 技术基于两个阈值创建了一个简单的异常检测系统，并且我们还解释了在处理这类问题时必须考虑哪些因素。

在最后一部分中，我们分析了可用于执行新颖性检测的两种常用方法。 一类 SVM 利用核函数将复杂的数据集投影到可以线性分离的特征空间上。 下一步基于这样的假设：所有训练集（一小部分除外）都是内在者，因此它们属于同一类。 训练该模型的目的是最大程度地缩小内部节点与特征空间原点之间的距离，并且结果基于样本相对于分离超平面的位置。 相反，孤立森林是一种集成模型，基于以下假设：离群值从随机训练的决策树中的根到样本的路径平均较短。

因此，在训练森林之后，可以考虑给定新样本的平均路径长度来计算异常分数。 当该分数接近 1 时，我们可以得出结论，异常的可能性也很大。 相反，非常小的得分值表明该新颖性是潜在的内在值。

在下一章中，我们将讨论降维和字典学习的最常用技术，当有必要管理具有大量特征的数据集时，这些技术将非常有用。

问题

1. 一个人身高 1.70m 的概率为p(Tall) = 0.75，而明天要下雨的概率为P(Rain) = 0.2。 p(Tall, Rain)的概率是多少？ （即一个人身高 1.70m，明天要下雨的概率）。
2. 给定数据集X，我们构建了一个具有 1,000 个桶的直方图，我们发现其中许多是空的。 为什么会这样？
3. 直方图包含三个分别具有 20、30 和 25 个样本的桶。 第一个容器的范围为0 < x < 2，第二个2 < x < 4，第三4 < x < 6。 P(x) > 2的大概概率是多少？
4. 给定正态分布N(0, 1)，可以将p(x) = 0.35的样本x视为异常吗？
5. 具有 500 个样本的数据集X具有std(X) = 2.5和IQR(X) = 3.0。 最佳带宽是多少？
6. 一位专家告诉我们，分布在两个值附近都达到了峰值，并且密度突然从峰均值下降了 0.2 个标准差。 哪种内核最合适？
7. 给定样本x（从 10,000 个样本的流人口中收集），我们不确定这是异常还是新颖，因为p(x) = 0.0005。 再进行 10,000 次观察后，我们重新训练模型，x保持p(x) < 0.001。 我们可以得出结论x是异常吗？

进一步阅读

• Epanechnikov V A, Non-parametric estimation of a multivariate probability density, Theory of Probability and its Applications, 14, 1969

• Parzen E, On Estimation of a Probability Density Function and Mode, The Annals of Mathematical Statistics, 1962

• Sheather S J, The performance of six popular bandwidth selection methods on some real data sets (with discussion), Computational Statistics, 7, 1992

• Schölkopf B, Platt J C, Shawe-Taylor J C, Smola A J, Williamson R C, Estimating the support of a high-dimensional distribution, Neural Computation, 13/7, 2001

• Liu F T, Ting K M, Zhou Z, Isolation forest, ICDM 2008, Eighth IEEE International Conference on Data Mining, 2008

• Dayan P, Abbott L F, Theoretical Neuroscience, The MIT Press, 2005

• Machine Learning Algorithms Second Edition, Bonaccorso G., Packt Publishing, 2018

七、降维和成分分析

在本章中，我们将介绍和讨论一些非常重要的技术，这些技术可用于执行降维和成分提取。 在前一种情况下，目标是将高维数据集转换为低维数据集，以尽量减少信息丢失量。 后者是找到可以混合的原子字典以构建样本所需的过程。

特别是，我们将讨论以下主题：

• 主成分分析（PCA）
• 奇异值分解（SVD）和增白
• 核 PCA
• 稀疏的 PCA 和字典学习
• 因子分析
• 独立成分分析（ICA）
• 非负矩阵分解（NNMF）
• 潜在狄利克雷分布（LDA）

技术要求

本章将介绍的代码需要以下内容：

• Python3.5+（强烈建议使用 Anaconda 发行版）
• 以下库：
  • SciPy 0.19+
  • NumPy 1.10+
  • Scikit-Learn 0.20+
  • Pandas 0.22+
  • Matplotlib 2.0+
  • Seaborn 0.9+

可以在 GitHub 存储库中找到这些示例。

主成分分析（PCA）

减少数据集维数的最常见方法之一是基于样本协方差矩阵的分析。 通常，我们知道随机变量的信息内容与其方差成正比。 例如，给定多元高斯，熵是我们用来测量信息的数学表达式，如下所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-h0HbsDjI-1681652675144)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/998f8f17-4c20-4dfa-952f-7c14ed957bae.png)]

在前面的公式中，Σ是协方差矩阵。 如果我们假设（不失一般性）Σ是对角线，那么很容易理解，熵（成比例地）大于每个单个分量的方差σ[i]^2。 这不足为奇，因为方差低的随机变量集中在均值附近，出现意外的可能性低。 另一方面，当σ^2变得越来越大时，潜在结果随着不确定性而增加，不确定性与信息量成正比。

当然，组件的影响通常是不同的； 因此，主成分分析（PCA）的目标是，可以找到可以将其投影到较低维子空间的样本的线性变换，来保持最大的初始方差量。 实际上，让我们考虑一个数据集X ∈ G^(m×n)：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Hn6a7vu0-1681652675144)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/f228a482-b17a-47db-a19c-cdce3779555f.png)]

我们要查找的线性变换是一个新的数据集，如下所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jTlaxDBZ-1681652675144)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/65cd1e88-dafd-4d51-93c0-05433565fd21.png)]

应用了这样的转换后，我们期望具有以下内容：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-T4DAOP1h-1681652675144)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/8d580e00-60fa-4ec8-868e-5dcb5b9752ee.png)]

让我们开始考虑样本协方差矩阵（出于我们的目的，我们也可以采用有偏估计）； 为简单起见，我们还将假设X的均值为零：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zoPYNqXc-1681652675144)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/94f59483-b3b0-42b8-881b-8f88e1a42b51.png)]

这样的矩阵是对称的且是正半定的（如果您不熟悉这些概念并不重要，但是它们对于证明以下步骤非常重要），因此其特征向量构成了正交标准。 快速回顾一下，如果A是方阵，则将v[i]的向量称为与特征值v[i]，如果满足以下条件：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-O8zGtGaP-1681652675145)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/84f43f25-9b2e-4994-b580-27d4922e5c70.png)]

换句话说，特征向量被转换为自身的扩展或压缩版本（不会发生旋转）。 证明协方差矩阵的特征向量定义协方差分量的方向（即数据集具有特定协方差分量的方向）并不难（但将省略所有数学细节）。 原因很简单； 实际上，在变换之后，新的协方差矩阵（变换后的数据集Z）是不相关的（即，它是对角线的），因为新轴与协方差分量对齐。 这意味着将向量（例如，v[0] = (1, 0, 0, ..., 0)）转换为σ[i]^2 v[i]，因此它是一个特征向量，其相关特征值与第i个分量的方差成比例 。

因此，为了找出可以丢弃的元素，我们可以对特征值进行排序，以便满足以下条件：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mVtkGb7s-1681652675145)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/1fc1b1d5-1d32-426c-9723-8a559c1b09b0.png)]

相应的特征向量v[1], v[2], ..., v[n]分别确定对应最大方差的成分，依此类推，直到最后一个。 形式上，我们将特征向量定义为主成分； 因此，第一个主成分是与最大方差相关的方向，第二个主成分与第一个主方正交，并且与第二个最大方差相关，依此类推。 对于二维数据集，此概念显示在以下屏幕截图中：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9Sv3Yv7O-1681652675145)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/b93e1305-0337-4224-b77d-22119c907841.png)]

二维数据集的主成分； 第一个主成分沿着方差最大的轴，而第二个主成分正交，并且与剩余方差成比例

至此，问题几乎解决了。 实际上，如果仅选择第一个k主成分（v[i] ∈ R^(n×1)），则可以构建一个变换矩阵A[k] ∈ R^(n×k)，从而使特征向量与前k个特征值列：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VLZwjt5g-1681652675145)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/25fc3f0b-9a46-4ae7-9ae1-e4fc48a72eda.png)]

因此，我们可以使用以下矩阵乘法来转换整个数据集：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tQXMNARv-1681652675145)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/b34ef798-1103-49d5-ab68-e75859ae3600.png)]

新数据集Z的维数等于k < n（或<<），并且它包含与分量数量成比例的原始变化量。 例如，考虑上一个屏幕快照中显示的示例，如果我们选择单个分量，则所有向量都将沿着第一个主分量变换为点。 当然，会有一些信息丢失，必须逐案考虑； 在以下各节中，我们将讨论如何评估此类损失并做出合理的决定。 现在，我们将简要展示如何以有效方式提取主要成分。

具有奇异值分解的 PCA

即使我们将采用完整的 PCA 实现，了解如何有效地执行此过程也将有所帮助。 当然，最明显的处理方法是基于样本协方差矩阵的计算，其特征分解（将输出特征值和对应的特征向量），然后最后可以构建变换矩阵。 这种方法很简单，但不幸的是，它效率也不高。 主要原因是我们需要计算样本协方差矩阵，这对于大型数据集而言可能是一项非常长的任务。

奇异值分解（SVD）提供了一种更为有效的方法，它是一种线性代数程序，具有一些重要特征：它可以直接在数据集上操作，当提取了所需数量的组件时可以停止，并且有增量版本可以小批量工作，从而解决了内存不足的问题。 特别地，考虑到数据集X ∈ R^(m×n)，SVD 可以表示为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LRN4yzfD-1681652675146)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/8c7d96e8-429e-41e8-b107-4f95d67c39c3.png)]

U是一个正交矩阵（即UU^T = U^T U = I，因此U^T = U^(-1)），其中左手奇异向量作为行（XX^T的特征向量）；V（也为正交）包含右手奇异向量作为行（对应于X^T X的特征向量），而Λ是一个对角矩阵，包含$1[$2]的奇异值（这是XX^T和X^T X的特征值的平方根）。 特征值按降序排序，特征向量重新排列以匹配相应位置。 由于1 / m因子是一个乘法常数，因此它不会影响特征值的相对大小； 因此，排序顺序保持不变。 因此，我们可以直接使用V或U进行工作，并从Λ中选择第一个顶部k特征值。 特别是，我们可以观察到以下结果（因为变换矩阵A等于V）：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OHP6L0K8-1681652675146)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/2a969f33-17b7-4f4b-b322-238daea5f0e2.png)]

因此，通过使用U[k]（仅包含顶部k特征向量）和U[k]]（仅包含顶部的k特征值），我们可以直接获得较低维的转换数据集（具有k分量），如下所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rU4asaO1-1681652675146)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/6d9ea074-b25a-4353-8526-ec0675049126.png)]

此方法快速，有效，并且在数据集太大而无法放入内存时可以轻松扩展。 即使我们在本书中不使用此类场景，也值得一提的是 scikit-learn TruncatedSVD 类（其 SVD 限于k最高特征值）和IncrementalPCA 类（小批量执行 PCA）。 为了我们的目的，我们将使用标准的PCA类和一些重要的变体，它们要求整个数据集都适合内存。

白化

SVD 的一个重要应用是白化程序，该程序强制以空平均值（即E[X] = 0）对数据集X或零中心），以具有恒等式的协方差矩阵C。 该方法对提高许多监督算法的表现非常有帮助，这可以受益于所有组件共享的统一单一方差。

将分解应用于C，我们获得以下信息：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MSY19Fqj-1681652675146)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/29e02839-8777-46c9-a39f-f5c829986992.png)]

矩阵V的列是C的特征向量，而Λ是包含特征值的对角矩阵（请记住，SVD 输出奇异值，它们是特征向量的平方根）。 因此，我们需要找到一个线性变换，z = Ax，以便E[Z^T Z] = I。 使用先前的分解时，这很简单：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pYnygpTi-1681652675146)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/523c33c0-9701-494f-9c60-8532278de6ab.png)]

从前面的方程式中，我们可以得出变换矩阵A的表达式：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PknzN6Tl-1681652675147)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/2c719331-b8b9-4519-991b-8fc82bacea52.png)]

现在，我们将通过一个小的测试数据集展示美白效果，如下所示：

import numpy as np

from sklearn.datasets import make_blobs

X, _ = make_blobs(n_samples=300, centers=1, cluster_std=2.5, random_state=1000)

print(np.cov(X.T))

前一个块的输出显示了数据集的协方差矩阵，如下所示：

[[6.37258226 0.40799363]
 [0.40799363 6.32083501]]

以下代码段显示了whiten() 函数，该函数用于对通用数据集进行美白（零居中是过程的一部分）（correct参数在漂白之后强制执行缩放校正）：

import numpy as np

def zero_center(X):
    return X - np.mean(X, axis=0)

def whiten(X, correct=True):
    Xc = zero_center(X)
    _, L, V = np.linalg.svd(Xc)
    W = np.dot(V.T, np.diag(1.0 / L))
    return np.dot(Xc, W) * np.sqrt(X.shape[0]) if correct else 1.0

以下屏幕截图显示了应用于X 数组的增白结果：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1kuSFg8G-1681652675147)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/96f5814c-722a-4892-aecb-e31d1b885cc7.png)]

原始数据集（左）； 白化的数据集（右）

现在，我们可以检查新的协方差矩阵，如下所示：

import numpy as np

Xw = whiten(X)
print(np.cov(Xw.T))

输出如下：

[[1.00334448e+00 1.78229783e-17]
 [1.78229783e-17 1.00334448e+00]]

可以看到，矩阵现在是一个恒等式（具有最小的误差），并且数据集也具有空均值。

具有 MNIST 数据集的 PCA

现在，让我们应用 PCA，以减少 MNIST 数据集的维数。 我们将使用 scikit-learn 提供的压缩版本（1,797，8×8 图像），但是我们的考虑都不会受到此选择的影响。 让我们从加载和规范化数据集开始：

from sklearn.datasets import load_digits

digits = load_digits()
X = digits['data'] / np.max(digits['data'])

从理论讨论中，我们知道协方差矩阵的特征值的大小与相应主成分的相对重要性（即，所解释的方差，因此是信息含量）成正比。 因此，如果将它们按降序排序，则可以计算以下差异：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9wcm7GFO-1681652675147)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/75540aa4-e15b-4bc0-8ffa-f81647e70fc7.png)]

当k → n的数量变得越来越重要时，我们可以通过选择第一个最大的差值来选择最佳的k，这表明所解释的数量大大减少了。 以下所有组件的差异。 为了更好地理解这种机制，让我们计算特征值和它们的差异（由于协方差矩阵C是正半确定的，因此我们确定λ[i] ≥ 0, ∀i ∈ (1, n)）：

import numpy as np

C = np.cov(X.T)
l, v = np.linalg.eig(C)
l = np.sort(l)[::-1]
d = l[:l.shape[0]-1] - l[1:]

以下屏幕快照显示了展开图像（64 维数组）的差异：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZO18wUhi-1681652675147)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/8109d275-c6a0-42c6-b8cb-b7f2a22c590f.png)]

每个主成分的特征值差异

可以看出，第一主成分的差异非常大，与第四主成分（λ[4] - λ[3]）； 但是，下一个差异仍然很高，虽然对应$1[$2]突然下降。 在这一点上，趋势几乎是稳定的（除了一些残余振荡），直到$1[$2]为止，然后趋势开始迅速下降，趋于趋于零 。 由于我们仍然希望获得正方形图像，因此我们将选择k = 16（相当于将每一边除以四）。 在另一个任务中，您可以选择k = 15，甚至k = 8； 但是，为了更好地理解降维导致的误差，也将有助于分析所解释的方差。 因此，让我们从执行 PCA 开始：

from sklearn.decomposition import PCA

pca = PCA(n_components=16, random_state=1000)
digits_pca = pca.fit_transform(X)

在拟合模型并将所有样本投影到对应于前 16 个主成分的子空间后，即可获得digits_pca 数组。 如果我们想将原始图像与其重构进行比较，则需要调用inverse_transform() 方法，该方法将投影投射到原始空间上。 因此，如果 PCA 在这种情况下是变换f(x): ℜ^64 → ℜ^16，则逆变换为g(x): ℜ^16 → ℜ^64。 以下屏幕截图显示了前 10 位数字与它们的重构之间的比较：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aJAVkIn5-1681652675147)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/6b57796e-5007-448a-9bd2-a96bc7e3affb.png)]

原始样本（第一行）； 重建（底部行）

重建显然是有损的，但是数字仍然是可区分的。 现在，让我们通过对explained_variance_ratio_ 数组的所有值求和来检查总的解释方差，其中包含每个分量的相对解释方差的相对数量（因此，任何k < n分量始终小于 1）：

print(np.sum(pca.explained_variance_ratio_))

上一个代码段的输出如下：

0.8493974642542452

因此，在将维数减少到 16 个分量的情况下，考虑到每个样本都将丢弃 48 个分量，我们正在解释原始差异的 85%，这是一个合理的值。

以下屏幕快照显示了显示所有单个贡献的图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VWPP6ZND-1681652675148)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/f34df112-3c13-4331-b106-31b3c662783d.png)]

对应每个主成分的解释方差比

正如预期的那样，贡献趋于减少，因为在这种情况下，第一个主要成分负责任； 例如，对于一种颜色的线条（例如黑色或白色），而其余的则为灰色。 这种行为非常普遍，几乎在每种情况下都可以观察到。 通过该图，还可以轻松找到额外的损失，以进一步减少损失。 例如，我们可以立即发现，对 3 个成分的严格限制可以解释原始差异的 40% ； 因此，剩余的 45% 被分为剩余的 13 个组成部分。 我邀请您重复此示例，尝试找出人类区分所有数字所需的最少数量的组件。

核 PCA

有时，数据集不是线性可分离的，并且标准 PCA 无法提取正确的主成分。 当我们面对非凸群集的问题时，该过程与第 3 章，“高级聚类”中讨论的过程没有什么不同。 在那种情况下，由于几何原因，某些算法无法执行成功的分离。 在这种情况下，目标是根据主成分的结构区分不同的类（在纯净，无监督的情况下，我们考虑特定的分组）。 因此，我们要使用转换后的数据集Z，并检测可区分阈值的存在。 例如，让我们考虑以下屏幕截图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HMBnmn1o-1681652675148)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/1152710f-83cd-449a-9389-5540bb9ad014.png)]

原始数据集（左）； PCA 投影版本（右）

由于原始数据集是线性可分离的，因此在 PCA 投影之后，我们可以立即找到允许检测第一个成分（这是真正需要的唯一成分）的阈值，以便区分两个斑点。 但是，如果数据集不是线性可分离的，我们将得到不可接受的结果，如以下屏幕截图所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Pfc5jloH-1681652675148)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/d2439c67-b819-4557-9e0a-c50a1e0178b5.png)]

原始数据集（左）； PCA 投影版本（右）

当几何形状更复杂时，找到可区分的阈值可能是不可能的。 但是，我们知道，将数据投影到高维空间可以使它们线性分离。 特别地，如果x ∈ ℜ^n，我们可以选择适当的函数f(x)，这样y = f(x) ∈ ℜ^p，以及p >> n。 不幸的是，将这种转换应用于整个数据集可能会非常昂贵。 实际上，给定一个转换矩阵A（具有n个组件），一个主分量，a(t)投影后的可以编写如下（请记住它们是协方差矩阵的特征向量）：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EREl4ubw-1681652675148)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/0b373061-285c-4f7a-aadc-13d1e235a978.png)]

因此，单个向量的转换如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DAsKPL81-1681652675148)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/febdde35-860f-4ead-b585-97c81169aa6a.png)]

可以看到，转换需要计算点积f(x[i])^T f(x[i])。 在这些情况下，我们可以采用所谓的核技巧，该技巧指出存在称为核且具有有趣特性的特定函数K(·, ·)，如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UkqM8Zzc-1681652675149)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/d4f72e86-05e8-4d2e-8030-cc028ce9c8c1.png)]

换句话说，我们可以通过仅计算每两个点的内核，而不是执行一个点积来计算在高维空间中的主成分上的投影，该点积在计算后需要n乘法f(·)的值。

一些常见的核如下：

• 径向基函数（RBF）或高斯核：

  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VaHhVd75-1681652675149)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/be7df07d-e755-4712-9b16-409ec45c4d9d.png)]

• p为多项式核：

  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZAOt1Ci0-1681652675149)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/464465b9-c466-4538-8f60-33259f9424d7.png)]

• Sigmoid 核：

  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ar89K12h-1681652675149)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/f1b5b271-2c9d-46d2-99c5-e00687a24f4c.png)]

对于非常大的数据集，该过程仍然相当昂贵（但是可以预先计算并存储内核值，以避免浪费额外的时间），但是它比标准投影更有效。 此外，其具有允许在可能进行线性辨别的空间中提取主要成分的优点。 现在，让我们将 RBF 核 PCA 应用于上一个屏幕快照中显示的半月数据集。 gamma 参数等于1 /σ^2。 在这种特殊情况下，主要问题是存在双重重叠。 考虑到原始标准差约为 1.0（即σ^2 = 1），我们至少需要三个标准差才能适当区分他们; 因此，我们将设置γ = 10：

from sklearn.datasets import make_moons
from sklearn.decomposition import KernelPCA

X, Y = make_moons(n_samples=800, noise=0.05, random_state=1000)

kpca = KernelPCA(n_components=2, kernel='rbf', gamma=10.0, random_state=1000)
X_pca = kpca.fit_transform(X)

投影结果显示在以下屏幕截图中：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JvNXlyIW-1681652675149)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/2f600a98-54fb-439c-8be8-898b4650d05c.png)]

原始数据集（左）；核 PCA 投影版本（右）

可以看到，即使在这种情况下，第一个分量也足以做出决定（由于噪声，公差最小），将阈值设置为零可以分离数据集。 我邀请读者测试其他内核的效果并应用它们，以区分包含所有零和一的 MNIST 子集。

通过因子分析为异方差噪声添加更多鲁棒性

标准 PCA 的主要问题之一是这种模型在异方差噪声方面的固有弱点。 如果您不熟悉此术语，则引入两个定义将很有帮助。 多元去相关噪声项的特征在于对角协方差矩阵C，该矩阵可以具有两种不同的配置，如下所示：

• C = diag(σ^2, σ^2, ..., σ^2)：在这种情况下，噪声定义为同调（所有分量均具有相同的方差）。
• C = diag(σ[1]^2, σ[2]^2, ..., σ[n]^2)，其中σ[1]^2 ≠ σ[2]^2 ≠ ... ≠σ[n]^2：在这种情况下，噪声定义为异方差（每个分量都有其自身的方差）。

有可能证明，当噪声是同调的时，PCA 可以轻松地对其进行管理，因为单个分量的解释方差以相同的方式受噪声项的影响（也就是说，这等同于不存在噪声）。 相反，当噪声为异方差时，PCA 的表现将下降，其结果可能绝对不可接受。 因此，Rubin 和 Thayer（在《用于 ML 因子分析的 EM 算法》中）提出了另一种降维方法，称为因子分析，它可以解决此类问题。

假设我们有一个零中心数据集X，其中包含m个样本x[i] ∈ ℜ^n。 我们的目标是找到一组潜在变量，z[i] ∈ ℜ^p（其中p < n）和矩阵A（称为因子加载矩阵），以便可以重写每个样本，如下所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SmRzfxPW-1681652675150)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/f30e647b-5fcb-4fb0-a0fc-26e5698a673d.png)]

因此，我们现在假设样本x[i]是一组高斯潜变量加上一个额外的异方差噪声项的组合。 由于潜在变量的维数较低，因此问题与标准 PCA 非常相似，主要区别在于，我们现在考虑了异方差噪声（当然，n项也可以为null，或者同调）。 因此，当确定分量（即潜在变量）时，模型中将包括不同噪声方差的影响，最终效果是部分滤波（降噪）。 在上述论文中，作者提出了一种优化算法，该算法形式上不是很复杂，但是需要许多数学操作（因此，我们省略了任何证明）。 此方法基于期望最大化（EM）算法，该算法有助于查找使对数似然性最大化的参数集。 在本书中，我们无需讨论所有数学细节（可在原始论文中找到），而是检查该方法的属性并将结果与​​标准 PCA 进行比较。

让我们首先加载 Olivetti 人脸数据集，将其零居中，然后创建一个异方差嘈杂的版本，如下所示：

import numpy as np

from sklearn.datasets import fetch_olivetti_faces

faces = fetch_olivetti_faces(shuffle=True, random_state=1000)
X = faces['data']
Xz = X - np.mean(X, axis=0)

C = np.diag(np.random.uniform(0.0, 0.1, size=Xz.shape[1]))
Xnz = Xz + np.random.multivariate_normal(np.zeros(shape=Xz.shape[1]), C, size=Xz.shape[0])

以下屏幕截图显示了一些原始图像和嘈杂图像：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DRWSVvIb-1681652675150)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/6ceb7a52-0d18-4da0-9da0-a94f57f47c6e.png)]

原始图像（上一行）； 嘈杂的版本（下一行）

现在，让我们评估以下各项的平均对数似然率（通过score() 方法，PCA和FactorAnalysis类均可用的）：

• PCA，具有原始数据集和128组件
• PCA，带有嘈杂的数据集和128组件
• 因子分析，带有嘈杂的数据集和128分量（潜在变量）

在以下代码段中，所有 3 个模型都被实例化和训练：

from sklearn.decomposition import PCA, FactorAnalysis

pca = PCA(n_components=128, random_state=1000)
pca.fit(Xz)
print('PCA log-likelihood(Xz): {}'.format(pca.score(Xz)))

pcan = PCA(n_components=128, random_state=1000)
pcan.fit(Xnz)
print('PCA log-likelihood(Xnz): {}'.format(pcan.score(Xnz)))

fa = FactorAnalysis(n_components=128, random_state=1000)
fa.fit(Xnz)
print('Factor Analysis log-likelihood(Xnz): {}'.format(fa.score(Xnz)))

上一个代码段的输出如下：

PCA log-likelihood(Xz): 4657.3828125
PCA log-likelihood(Xnz): -2426.302304948351
Factor Analysis log-likelihood(Xnz): 1459.2912218162423

这些结果表明存在异方差噪声时因素分析的有效性。 PCA 实现的最大平均对数似然度约为4657，在存在噪声的情况下降至-2426。 相反，因子分析获得的平均对数似然率约为 1,460，这比使用 PCA 获得的对数似然率大得多（即使尚未完全滤除噪声的影响）。 因此，每当数据集包含（或数据科学家怀疑包含）异方差噪声时（例如，样本是作为不同仪器捕获的源的叠加而获得的），我强烈建议将因子分析作为主要的降维方法。 当然，如果要求其他条件（例如，非线性，稀疏性等），则可以在做出最终决定之前评估本章中讨论的其他方法。

稀疏的 PCA 和字典学习

标准 PCA 通常是密集分解； 这就是说，向量一旦转换，便是所有具有非零系数的分量的线性组合：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NFc40Gy8-1681652675150)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/6d321ec9-2ff5-4b21-8c88-e47d435bf51a.png)]

在前面的表达式中，系数$1[$2]几乎总是不为零，因此所有组件都参与重建过程。 出于降维的目的，这不是问题，因为为了限制它们，我们对每个组件解释的方差更感兴趣。 但是，在某些任务下，分析每个较大的构建原子很有帮助，并假设每个向量都可以表示为它们的稀疏组合。 最经典的例子是文本语料库，其中词典包含的项目比每个文档中涉及的项目更多。 这些类型的模型通常称为字典学习算法，因为原子集定义了一种字典，其中包含可用于创建新样本的所有单词。 当原子数k大于样本的维数n时，该字典被称为过度完成，其表示通常是稀疏的。 相反，当k < n时，字典被称为尚未完成，并且向量需要更密集。

通过对函数的最小化，对解决方案的L[1]范数施加惩罚，可以轻松解决此类学习问题。 这种限制导致稀疏性的原因不在本书的讨论范围之内，但是有兴趣的人可以在《Mastering Machine Learning Algorithms》中找到更长的讨论范围。

字典学习（以及稀疏 PCA）的问题可以正式表示为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qs55gP0X-1681652675150)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/b671cd38-0abc-483b-bf3d-80dfa23c6a65.png)]

这是一种算法的特殊情况，其中U[k]的分量被强制具有单位长度（除非normalize_components=False 参数） ，并对系数V进行了惩罚，以增加其稀疏度（与系数α成比例）。

让我们考虑 MNIST 数据集，它执行具有 30 个成分的稀疏 PCA（产生不完全的字典）和中高稀疏度（例如α = 2.0）。 数组X应该包含归一化的样本，并在以下 PCA 示例中显示：

from sklearn.decomposition import SparsePCA

spca = SparsePCA(n_components=30, alpha=2.0, normalize_components=True, random_state=1000)
spca.fit(X)

在训练过程结束时，components_ 数组包含原子，如以下屏幕快照所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yGeTzHJq-1681652675151)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/da76643e-d124-44d4-8547-a59042c1190b.png)]

稀疏 PCA 算法提取的成分

不难理解，每个数字都可以由这些原子组成。 但是，考虑到原子数，稀疏度不能非常大。 例如，考虑数字X[0]的转换：

y = spca.transform(X[0].reshape(1, -1)).squeeze()

以下屏幕快照显示了系数的绝对值：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DIHsVP8O-1681652675151)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/b9997b84-83e2-4bf5-a810-a95a8d0191d1.png)]

X[0]的稀疏转换的绝对系数

显然有一些主要成分（例如 2，7，13，17，21，24，26，27 和 30 ），一些次要的（例如 5，8 等）和一些无效或可忽略的值（例如 1，3，6 等）。 如果以相同的代码长度（30 个分量）增加稀疏度，则对应于空分量的系数将降至零，而如果代码长度也增加（例如k = 100） ，字典将变得过于完整，并且空系数的数量也将增加。

非负矩阵分解

当数据集X为非负数时，可以应用已被证明的分解技术（例如，在《通过非负矩阵分解学习对象的部分》中）在任务目标是提取与样本结构部分相对应的原子时更加可靠。 例如，在图像的情况下，它们应该是几何元素，甚至是更复杂的部分。 非负矩阵分解（NNMF）施加的主要条件是，所有涉及的矩阵都必须为非负，并且X = UV。 因此，一旦定义了标准N（例如 Frobenius），则简单目标就变成了：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tYjmUTmx-1681652675151)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/f554b0eb-d763-49ca-a7c2-6916ff5e9523.png)]

由于这在通常还需要稀疏性的情况下通常是不可接受的（而且，为了在更改解决方案以满足特定要求时具有更大的灵活性），因此通常通过在两个 Frobenius 上加点惩罚来表达该问题（例如在 scikit-learn 中） （L[2]的矩阵扩展）和L[1]规范（例如，在 ElasticNet 中）：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-opj5m4Sc-1681652675151)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/b12f42f8-c6ae-4a84-b399-061168e10d1c.png)]

双重正则化通过避免类似于监督模型的过拟合的效果，使您既可以获得稀疏性，又可以获得样本的各部分之间的更好匹配（由于该解决方案次优，因此在适应新模型时更加灵活） 样本是从相同的数据生成过程中提取的；这增加了通常可以实现的可能性）。

现在，让我们考虑 MNIST 数据集，并将其分解为 50 个原子，最初设置α = 2.0和β = 0.1（在 scikit-learn 中称为l1_ratio）。 此配置将强制中等稀疏性和强 L2/Frobenius 正则化。 该过程非常简单，类似于稀疏 PCA：

from sklearn.decomposition import NMF

nmf = NMF(n_components=50, alpha=2.0, l1_ratio=0.1, random_state=1000)
nmf.fit(X)

在训练过程结束时，组件（原子）如以下屏幕快照所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kHAVkrTC-1681652675151)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/fc28caef-8e14-4593-a2dc-6162aaed6ed5.png)]

NNMF 算法提取的原子

与我们在标准字典学习中观察到的相反，原子现在结构化了很多，并且它们再现了数字的特定部分（例如，垂直或水平笔画，圆，点等）； 因此，我们可以预期会有更多的稀疏表示，因为更少的组件足以构成一个数字。 考虑上一节中显示的示例（数字X[0]），所有组件的绝对贡献如下图所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uVhliJYi-1681652675152)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/9cea1dd3-7125-426d-adf4-3a4801c7d2a4.png)]

X[0]的 NNMF 的绝对系数

占主导地位的是三个部分（ 3 ， 24 和 45 ）； 因此，我们可以尝试将样本表示为它们的组合。 系数分别为 0.19、0.18 和 0.16。 结果显示在以下屏幕截图中（数字X[0]代表零）：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oOv9DHG0-1681652675152)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/b7dc5e46-5859-49af-be9f-87b09a6bf01a.png)]

基于三个主成分来解构数字X[0]

有趣的是，该算法是如何选择原子的。 即使此过程受到α和β参数，以及规范的强烈影响，我们也可以观察到，例如，第三个原子（ 屏幕截图中的第一个）可以被许多零，三和八共享； 最后一个原子对于零和九都是有帮助的。 每当原子的粒度太粗糙时，具有较弱的L[1]罚分的不完整字典可能会有所帮助。 当然，每个问题都需要特定的解决方案。 因此，我强烈建议与领域专家一起检查原子的结构。 作为练习，我邀请您将 NNMF 应用于另一个小图像数据集（例如 Olivetti，Cifar-10 或 STL-10），并尝试找到隔离固定数量的结构零件所必需的正确参数（ 例如，对于人脸，它们可以是眼睛，鼻子和嘴巴。

独立成分分析

当使用标准 PCA（或其他技术，例如因子分析）时，组件是不相关的，但是不能保证它们在统计上是独立的。 换句话说，假设我们有一个数据集X，它是从联合概率分布p(X)中得出的； 如果n个组件存在，我们不能总是确定以下等式成立：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FouuufP3-1681652675152)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/3b056214-1a06-43b5-97cd-0c1ee2e42303.png)]

但是，基于称为鸡尾酒会的通用模型，有许多重要任务。 在这种情况下，我们可以假设（或我们知道）许多不同且独立的源（例如声音和音乐）重叠并生成单个信号。 在这一点上，我们的目标是尝试通过对每个样本进行线性变换来分离源。 让我们考虑一个增白的数据集X（因此所有组件都具有相同的信息内容），我们可以假定是从高斯分布N(0, I)中采样的（ 这不是限制性条件，因为许多不同源的重叠很容易收敛到正态分布。 因此，目标可以表示如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jb92hzgg-1681652675152)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/ec86cdcc-2bc6-49b3-9bf8-1517b0a6ce34.png)]

换句话说，我们将每个样本表示为许多独立因素的乘积，并具有基于指数函数的先验分布。 必须绝对强制执行的唯一条件是非高斯性（否则，各组成部分将变得难以区分）。 因此，函数f[k](z)不能为二次多项式。 在实践中，我们还希望包括中等程度的稀疏性，因此我们期望出现峰值和重尾分布（也就是说，概率仅在非常短的范围内才很高，然后突然下降到几乎为零）。 这种情况可以通过检查归一化的第四矩峰度来验证：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mQj0YMWy-1681652675152)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/56c4514e-1b79-48f0-92ed-c4b0596ede4c.png)]

对于高斯分布，峰度为 3。由于这通常是一个参考值，因此所有具有Kurtosis(X) > 3的分布都称为超高斯或尖峰。 ，将具有Kurtosis(X) < 3的人称为亚高斯性或平峰。 前一个分配类别的示例是 Laplace 分配类别，如以下屏幕截图所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TUNIwWLH-1681652675153)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/fd260b15-bd75-4638-8be4-1f69c6c4d9a5.png)]

高斯分布（左）和拉普拉斯分布（右）的概率密度函数

不幸的是，峰度的使用由于其对异常值的缺乏鲁棒性而受到阻碍（也就是说，由于它涉及四次方，因此即使很小的值也可以被放大并改变最终结果；例如，噪声高斯的尾部的离群值可以显示为超高斯）。 因此，作者 Hyvarinen 和 Oja （在《独立组件分析：算法和应用》中）提出了一种称为快速独立组件分析（FastICA）基于负熵的概念。 我们不会在本书中描述整个模型。 但是，了解基本思想会有所帮助。 可以证明，在具有相同方差的所有分布之间，高斯熵最大。 因此，如果数据集X（零中心）已从具有协方差Σ的分布中得出，则可以定义X作为高斯N(0 ;Σ)的熵与X的熵之间的差

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-g51WrFWl-1681652675153)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/c69596e4-c1c9-4843-8a54-eaf1e7682f29.png)]

因此，我们的目标是通过减少J(X)来减少H[N](X)（始终大于或等于零）。 FastICA 算法基于特定特征的组合，近似于H[N](X)。 最常见的称为 logcosh （它也是 scikit-learn 中的默认值），如下所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HbY0QPlD-1681652675153)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/f733002f-7004-42d5-9f94-42f5be45dfd4.png)]

使用此技巧，可以更轻松地优化负熵，并且最终分解必定包含独立的成分。 现在，让我们将 FastICA 算法应用于 MNIST 数据集（为了提高精度，我们设置max_iter=10000和tol=1e-5）：

from sklearn.decomposition import FastICA

ica = FastICA(n_components=50, max_iter=10000, tol=1e-5, random_state=1000)
ica.fit(X)

以下屏幕快照显示了该算法找到的 50 个独立组件（始终通过components_ i 实例变量可用）。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2taDFvIZ-1681652675153)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/b7ee2fce-1609-4c31-aad4-e654090162b8.png)]

FastICA 提取的独立成分

在这种情况下，组件可以立即被识别为数字的一部分（考虑到数据集的维数，我邀请读者通过减少和增加组件的数量直至 64（这是最大数量）来重复该示例）。 这些分量趋于到达相应分布的平均位置。 因此，使用较少的数量，就可以区分出更多的结构化模式（可以视为不同的重叠信号），而使用更多的组件，则可以得到更多以特征为中心的元素。 但是，与 NNMF 相反，FastICA 不保证提取样本的实际部分，而是保证提取更完整的区域。 换句话说，尽管 NNMF 可以轻松检测到例如某些单个笔触，但 FastICA 倾向于将样本视为不同信号的总和，在图像的情况下，通常涉及样本的整个维数，除非组件数量急剧增加。 为了更好地理解这个概念，让我们考虑一下 Olivetti 人脸数据集，其中包含 400 张 64×64 灰度肖像：

from sklearn.datasets import fetch_olivetti_faces

faces = fetch_olivetti_faces(shuffle=True, random_state=1000)

以下屏幕截图显示了前 10 张面孔：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bFoAqhb8-1681652675154)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/b3216550-d65a-49d5-bbe3-902737f9ca8a.png)]

从 Olivetti 人脸数据集中提取的人脸样本

现在，让我们提取 100 个独立的组件：

ica = FastICA(n_components=100, max_iter=10000, tol=1e-5, random_state=1000)
ica.fit(faces['data'])

下面的屏幕截图绘制了前 50 个组件：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Rk4f8e8h-1681652675154)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/b70d1a5f-69b2-4c53-8dd1-1a48899153f2.png)]

50 (out of 100) independent components extracted by FastICA

如您所见，每个组成部分都类似于元人脸（有时称为特征人脸），由于所有其余部分（即使它们无法在精确的样本集中立即识别出来）。 当组件的数量增加到 350 时，效果将更加明显，如下所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RiFrbN5F-1681652675154)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/59bedc09-a9d7-4314-8e2b-85d92e82d73f.png)]

50 (out of 350) independent components extracted by FastICA

在这种情况下，次要特征不太占优势，因为存在更多的重叠分布，并且每个特征都集中在一个更原子的本征面上。 当然，如果没有完整的领域知识，就无法定义组件的最佳数量。 例如，对于 Olivetti 人脸数据集，识别特定的子元素（例如，眼镜的位置）或更完整的人脸表情可能会有所帮助。 在前一种情况下，更多的组件会产生更集中的解决方案（即使它们在全局范围内的区别性较小），而在后一种情况下，数量较少的组件（例如上一个示例）会产生更完整的结果，可以评估不同的影响因素。 就信号而言，组件的数量应等于预期的重叠因子的数量（假设其独立性）。 例如，音频信号可以包含在机场讲话的人的录音，并带有宣布飞行的背景声音。 在这种情况下，方案可以由三个部分组成：两个声音和噪音。 由于噪声将部分分解为主要成分，因此最终数量将等于 2。

潜在狄利克雷分布的主题建模

现在，我们将考虑另一种分解方法，这种分解方法在处理文本文档（即 NLP）时非常有用。 理论部分不是很容易，因为它需要对概率论和统计学习有深入的了解（可以在原始论文《隐迪利克雷分布》）； 因此，我们将只讨论主要元素，而没有任何数学参考（《机器学习算法第二版》）。 让我们考虑一组文本文件d[j]（称为语料库），其原子（或组成部分）为单词w[i]：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ztQejnci-1681652675154)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/1bd90156-21af-498a-a042-cfa962bb7146.png)]

收集所有单词后，我们可以构建一个词典：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dhf3pbKM-1681652675155)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/a874f7dd-cdea-4205-bde1-c602e0d85c9d.png)]

我们还可以陈述以下不等式（N(·)计算集合中元素的数量）：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mk3otdW9-1681652675155)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/c4808f1e-dcfe-4611-85da-902b9260a62c.png)]

这意味着文档之间单词的分布是稀疏的，因为在单个文档中只使用了很少的单词，而前者的选择是对称 Dirichlet 分布（该模型以此命名），它非常稀疏 （此外，它是分类分布的共轭先验，它是一阶多项式，因此很容易合并到模型中）。 概率密度函数（由于分布是对称的，因此α[i] = α ∀ i）如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-t73wSo1z-1681652675155)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/1efe3b99-cd8a-4aed-8c79-74a2fd406559.png)]

现在，让我们考虑将文档按主题进行语义分组，即t[k]，并假设每个主题都具有少量奇特词：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qItgZKif-1681652675155)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/4e47e13c-2fba-4f37-9b1b-7105ac0113fe.png)]

这意味着主题之间的单词分布也很少。 因此，我们具有完整的联合概率（单词，主题），并且我们想要确定条件概率p(w[i] | t[k])和p(t[k] | w[i])。 换句话说，给定一个文档，它是项目的集合（每个项目都有边际概率p(w[i])计算此类文档属于特定主题的概率。 由于一个文档被轻柔地分配给所有主题（也就是说，它可以在不同程度上属于一个以上的主题），因此我们需要考虑一个稀疏的主题文档分布，其中的主题组合（$1[$2]）被绘制为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kYxQhFfj-1681652675156)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/e168ebe0-4213-45f5-aa01-83a00d2af0b0.png)]

以类似的方式，我们需要考虑主题词的分布（因为一个词可以被更多的主题共享，程度不同），我们可以从中得出主题词-混合样本β[j]：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8hqxKZOj-1681652675157)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/92cf505a-127c-48d7-b166-8e5a743c9be2.png)]

潜在狄利克雷分布（LDA）是一个生成模型（训练目标以简单的方式包括找到最佳参数α和γ），它能够从语料库中提取固定数量的主题，并用一组单词来表征它们。 给定示例文档，它可以通过提供主题混合概率向量（θ[i] = (p(t[1]), p(t[2]), ..., p(t[k]))）；它也可以处理看不见的文档（使用同一词典）。

现在，让我们将 LDA 应用于 20 个新闻组数据集中的一个子集，其中包含数千个已公开发布以供 NLP 研究的消息。 特别是，我们要对rec.autos和comp.sys.mac.hardware子组建模。 我们可以使用内置的 scikit-learn fetch_20newsgroups()函数，要求去除所有不必要的页眉，页脚和引号（答案所附的其他帖子）：

from sklearn.datasets import fetch_20newsgroups

news = fetch_20newsgroups(subset='all', categories=('rec.autos', 'comp.sys.mac.hardware'), remove=('headers', 'footers', 'quotes'), random_state=1000)

corpus = news['data']
labels = news['target']

此时，我们需要对语料库进行向量化处理。 换句话说，我们需要将每个文档转换为包含词汇表中每个单词的频率（计数）的稀疏向量：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TZgMOj4M-1681652675157)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/0cd64574-1e19-462a-ac3b-8c618fcc6d34.png)]

我们将使用CountVectorizer 类，来执行此步骤，要求去除重音并删除停用词，例如，停用词的相对使用率很高，但不具有代表性。 此外，我们正在强制令牌生成器排除所有不是纯文本的令牌（通过设置token_pattern='[a-z]+'）。 在其他情况下，这种模式可能会有所不同，但是在这种情况下，我们不想依赖数字和符号：

from sklearn.feature_extraction.text import CountVectorizer

cv = CountVectorizer(strip_accents='unicode', stop_words='english', analyzer='word', token_pattern='[a-z]+')
Xc = cv.fit_transform(corpus)

print(len(cv.vocabulary_))

上一个代码段的输出如下：

14182

因此，每个文档都是一个 14182 维的稀疏向量（很明显，大多数值都是空的）。 现在，我们可以通过施加n_components=2来执行 LDA，因为我们希望提取两个主题：

from sklearn.decomposition import LatentDirichletAllocation

lda = LatentDirichletAllocation(n_components=2, learning_method='online', max_iter=100, random_state=1000)
Xl = lda.fit_transform(Xc)

在训练过程之后，components_ 实例变量包含每对夫妇（单词和主题）的相对频率（以计数为单位）。 因此，在我们的情况下，其形状为(2, 14, 182)，components_[i, j] 元素，且i ∈ (0, 1)和j ∈ (0, 14, 181)可以解释为单词j的重要性，以便定义主题i。 因此，我们将有兴趣检查两个主题的前 10 个词：

import numpy as np

Mwts_lda = np.argsort(lda.components_, axis=1)[::-1]

for t in range(2):
    print('\nTopic ' + str(t))
    for i in range(10):
        print(cv.get_feature_names()[Mwts_lda[t, i]])

输出如下：

Topic 0
compresion
progress
deliberate
dependency
preemptive
wv
nmsu
bpp
coexist
logically

Topic 1
argues
compromising
overtorque
moly
forbid
cautioned
sauber
explosion
eventual
agressive

易于理解（考虑一些非常特殊的项目），已将Topic 0分配给comp.sys.mac.hardware ，将另一个分配给rec.autos（不幸的是，此过程不能基于自动检测，因为语义必须由人解释）。 为了评估模型，让我们考虑两个示例消息，如下所示：

print(corpus[100])
print(corpus[200])

输出（限于几行）如下：

I'm trying to find some information on accelerator boards for the SE. Has
anyone used any in the past, especially those from Extreme Systems, Novy or
MacProducts? I'm looking for a board that will support extended video,
especially Radius's two-page monitor. Has anyone used Connectix Virtual in
conjunction with their board? Any software snafus? Are there any stats
anywhere on the speed difference between a board with an FPU and one
without? Please send mail directly to me. Thanks.

...

The new Cruisers DO NOT have independent suspension in the front.  They
still
run a straight axle, but with coils.  The 4Runner is the one with
independent
front.  The Cruisers have incredible wheel travel with this system. 

The 91-up Cruiser does have full time 4WD, but the center diff locks in
low range.  My brother has a 91 and is an incredibly sturdy vehicle which
has done all the 4+ trails in Moab without a tow.  The 93 and later is even
better with the bigger engine and locking diffs.

因此，第一个帖子显然与绘画有关，而第二个帖子是政治信息。 让我们为它们两者计算主题混合，如下所示：

print(Xl[100])
print(Xl[200])

输出如下：

[0.98512538 0.01487462]
[0.01528335 0.98471665]

因此，第一个消息大约有Topic 0的概率为 98%，而第二个消息几乎几乎没有分配给Topic 1。 这证实了分解工作正常。 为了更好地了解整体分布，可视化属于每个类别的消息的混合将很有帮助，如以下屏幕快照所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0BE13tLS-1681652675157)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/045bb9d5-9249-4207-8995-0d44461e6ec2.png)]

comp.sys.mac.hardware（左）和rec.autos（右）的主题组合

如您所见，主题几乎是正交的。 属于rec.autos的大多数消息具有p(t[0]) < 0.5和p(t[1]) > 0.5，而comp.sys.mac.hardware则略有重叠，其中不具有p(t[0]) > 0.5和p(t[1]) < 0.5的消息组稍大。 这可能是由于存在可以使两个主题具有相同重要性的词语（例如，讨论或辩论可能在两个新闻组中均出现）。 作为练习，我邀请您使用更多的子集，并尝试证明主题的正交性，并检测可能导致错误分配的单词。

总结

在本章中，我们介绍了可用于降维和字典学习的不同技术。 PCA 是一种非常知名的方法，涉及查找与方差较大的方向相关联的数据集的大部分导入成分。 该方法具有对角化协方差矩阵并立即测量每个特征的重要性的双重效果，从而简化了选择并最大化了剩余的解释方差（可以用较小的数字来解释的方差量） 组件）。 由于 PCA 本质上是一种线性方法，因此它通常不能与非线性数据集一起使用。 因此，已经开发了基于内核的变体。 在我们的示例中，您了解了 RBF 内核如何将非线性可分离的数据集投影到子空间，在该子空间中 PCA 可以确定判别分量。

稀疏 PCA 和字典学习是广泛使用的技术，当需要提取可以混合（以线性组合方式）的构建原子以生成样本时，可以使用这些技术。 在许多情况下，目标是找到一个所谓的“过度完成的字典”，这相当于说我们期望比构造每个样本的实际原子更多的原子（这就是为什么表示稀疏的原因）。 尽管 PCA 可以提取不相关的成分，但很少能够找到统计上独立的成分。 因此，我们引入了 ICA 的概念，该技术是为了从可以被认为是独立原因（例如，声音或视觉元素）之和的样本中提取重叠源而开发的。 具有特殊功能的另一种方法是 NNMF，它既可以生成稀疏表示，又可以生成类似于样本特定部分的一组组件（例如，对于人脸，它们可以表示眼睛，鼻子等）。 最后一部分介绍了 LDA 的概念，LDA 是一种主题建模技术，可以在给定文档主体（即文档属于每个特定主题的概率）的情况下查找主题组合。

在下一章中，我们将介绍一些基于无监督范式的神经模型。 特别地，将讨论可以在没有协方差矩阵的特征分解（或 SVD）的情况下提取数据集主成分的深度置信网络，自编码器和模型。

问题

1. 数据集X具有协方差矩阵C = diag(2, 1)。 您对 PCA 有什么期望？
2. 考虑到前面的问题，如果X居中于零，并且B[0.5](0, 0)*的球为空，我们可以假设一个阈值x = 0（第一个主要成分）是否允许水平判别？
3. PCA 提取的成分在统计上是独立的。 它是否正确？
4. Kurt(X) = 5的分布适用于 ICA。 它是否正确？
5. 包含样本(1, 2)和(0, -3)的数据集X的 NNMF 是多少？
6. 一个 10 个文档的语料库与一个带有 10 个词的词典相关联。 我们知道每个文档的固定长度为 30 个字。 字典是否过于完整？
7. 核 PCA 与二次内核一起使用。 如果原始大小为 2，则执行 PCA 的新空间的大小是多少？

进一步阅读

• Online Dictionary Learning for Sparse Coding, J. Mairal, F. Bach, J. Ponce, and G. Sapiro, 2009
• Learning the parts of objects by non-negative matrix factorization, Lee D. D., Seung S. H., Nature, 401, 10/1999
• EM algorithms for ML factor analysis, Rubin D., and Thayer D., Psychometrika, 47, 1982
• Independent Component Analysis: Algorithms and Applications, Hyvarinen A. and Oja E., Neural Networks 13, 2000
• Mathematical Foundations of Information Theory, Khinchin A. I., Dover Publications
• Latent Dirichlet Allocation, Journal of Machine Learning Research, Blei D., Ng A., and Jordan M., 3, (2003) 993-1022
• Machine Learning Algorithms Second Edition, Bonaccorso G., Packt Publishing, 2018
• Mastering Machine Learning Algorithms, Bonaccorso G., Packt Publishing, 2018

八、无监督神经网络模型

在本章中，我们将讨论一些可用于无监督任务的神经模型。 神经网络（通常是深层网络）的选择使您能够利用需要复杂处理单元（例如图像）的特定特征来解决高维数据集的复杂性。

特别是，我们将介绍以下内容：

• 自编码器
• 去噪自编码器
• 稀疏自编码器
• 变分自编码器
• PCA 神经网络：
• Sanger 网络
• Rubner-Attic 网络
• 无监督深度信念网络（DBN）

技术要求

本章中提供的代码要求以下内容：

• Python3.5+（强烈建议使用 Anaconda 发行版）
• 以下库：
  • SciPy 0.19+
  • NumPy 1.10+
  • Scikit-Learn 0.20+
  • Pandas 0.22+
  • Matplotlib 2.0+
  • Seaborn 0.9+
  • TensorFlow 1.5+
  • 深度信念网络

这些示例可在 GitHub 存储库中找到。

自编码器

在第 7 章，“降维和成分分析”中，我们讨论了一些通用的方法，这些方法可用于降低数据集的维数，因为其具有特殊的统计属性（例如协方差） 矩阵）。 但是，当复杂度增加时，即使核主成分分析（核 PCA）也可能找不到合适的低维表示形式。 换句话说，信息的丢失可以克服一个阈值，该阈值保证了有效重建样本的可能性。 自编码器是利用神经网络的极端非线性特性来查找给定数据集的低维表示的模型。 特别地，假设X是从数据生成过程中提取的一组样本，p_data(x)。 为简单起见，我们将考虑x[i] ∈ R^n，但对支撑结构没有任何限制（例如，对于 RGB 图像，x[i] ∈ R^(n×m×3)。 自编码器在形式上分为两个部分：有一个编码器，它将高维输入转换为较短的代码；一个解码器，执行逆运算（如下图所示）：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XMiikUa6-1681652675157)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/d2603e73-6156-40fe-b0f1-a2a37672819f.png)]

通用自编码器的结构模式

如果代码是p维向量，则可以将编码器定义为参数化函数e(·)：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Pl1pzhX6-1681652675158)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/f35b4488-e844-41a6-99a6-a2b984f4a7f7.png)]

以类似的方式，解码器是另一个参数化函数d(·)：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iviDdZ7t-1681652675158)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/9d31e248-bf97-42b4-a487-40dcbfbc3dce.png)]

因此，完整的自编码器是一个复合函数，在给定输入样本x[i]的情况下，它提供了最佳的输出重构：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cxSvzwn5-1681652675158)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/783c61af-8b57-4bb6-8e6a-cca350d5a8f7.png)]

由于通常是通过神经网络实现的，因此使用反向传播算法来训练自编码器，通常基于均方误差成本函数：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uo9LGGbw-1681652675158)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/588887de-3b03-4361-962f-883856470c8b.png)]

另外，考虑到数据生成过程，我们可以考虑参数化条件分布q(·)重新表达目标：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MPAfC7bS-1681652675158)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/3d870151-1e1f-4472-a9df-211ccc082726.png)]

因此，成本函数现在可以成为p_data(·)*和q(·)之间的 Kullback-Leibler 散度：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gufpXlmx-1681652675159)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/889fb37b-214d-4bd3-9e6d-d74c5343ae91.png)]

由于p_data的熵是一个常数，因此可以通过优化过程将其排除； 因此，散度的最小化等于p_data和q之间的交叉熵最小化。 如果假设p_data和q为高斯，则 Kullback-Leibler 成本函数等效于均方误差。 在某些情况下，当数据在(0, 1)范围内归一化时，可以对p_data和q采用伯努利分布。 形式上，这不是完全正确的，因为伯努利分布是二进制的，并且x[i] ∈ {0, 1}^d； 但是，使用 Sigmoid 输出单元还可以保证连续样本的成功优化， x[i] ∈ (0, 1)^d。 在这种情况下，成本函数变为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OA6pfYtZ-1681652675159)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/72f5d9d6-18c3-4216-b4e1-af7a8143feab.png)]

深度卷积自编码器的示例

让我们基于 TensorFlow 和 Olivetti faces 数据集（虽然相对较小，但提供良好的表现力）来实现深层卷积自编码器 。 让我们首先加载图像并准备训练集：

from sklearn.datasets import fetch_olivetti_faces

faces = fetch_olivetti_faces(shuffle=True, random_state=1000)
X_train = faces['images']

样本是 400 个64×64灰度图像，我们将其调整为32×32，以加快计算速度并避免出现内存问题（此操作会导致视觉精度略有下降，如果您有足够的计算资源，您可以删除它）。 现在，我们可以定义主要常量（周期数（nb_epochs，batch_size和code_length））和graph：

import tensorflow as tf

nb_epochs = 600
batch_size = 50
code_length = 256 
width = 32
height = 32

graph = tf.Graph() 

因此，我们将训练 600 个周期的模型，每批 50 个样本。 由于每个图像都是64×64 = 4,096，因此压缩率是4,096 / 256 = 16倍。 当然，这种选择不是规则，我邀请您始终检查不同的配置，以最大化收敛速度和最终精度。 在我们的案例中，我们正在对编码器进行以下建模：

• 具有 16 个3×3过滤器，2×2步幅，ReLU 激活和相同填充的 2D 卷积
• 具有 32 个3×3过滤器，1×1步幅，ReLU 激活和相同的填充的 2D 卷积
• 具有 64 个3×3过滤器，1×1跨距，ReLU 激活和相同的填充的 2D 卷积
• 2D 卷积，具有 128 个3×3个过滤器，1×1跨距，ReLU 激活和相同的填充

解码器利用一系列转置卷积（也称为反卷积）：

• 2D 转置卷积，具有 1283×3个过滤器，2×2步幅，ReLU 激活和相同的填充
• 具有 64 个3×3过滤器，1×1跨距，ReLU 激活和相同填充的 2D 转置卷积
• 具有 32 个3×3过滤器，1×1跨距，ReLU 激活和相同填充的 2D 转置卷积
• 2D 转置卷积，带有 13×3过滤器，1×1步幅，Sigmoid 激活，以及相同的填充

损失函数基于重构图像和原始图像之间差异的L[2]范数。 优化器是 Adam，学习率为η = 0.001。 TensorFlow DAG 的编码器部分如下：

import tensorflow as tf

with graph.as_default():
    input_images_xl = tf.placeholder(tf.float32, 
                                     shape=(None, X_train.shape[1], X_train.shape[2], 1))
    input_images = tf.image.resize_images(input_images_xl, (width, height), 
                                          method=tf.image.ResizeMethod.BICUBIC)

    # Encoder
    conv_0 = tf.layers.conv2d(inputs=input_images,
                              filters=16,
                              kernel_size=(3, 3),
                              strides=(2, 2),
                              activation=tf.nn.relu,
                              padding='same')

    conv_1 = tf.layers.conv2d(inputs=conv_0,
                              filters=32,
                              kernel_size=(3, 3),
                              activation=tf.nn.relu,
                              padding='same')

    conv_2 = tf.layers.conv2d(inputs=conv_1,
                              filters=64,
                              kernel_size=(3, 3),
                              activation=tf.nn.relu,
                              padding='same')

    conv_3 = tf.layers.conv2d(inputs=conv_2,
                              filters=128,
                              kernel_size=(3, 3),
                              activation=tf.nn.relu,
                              padding='same')

DAG 的代码部分如下：

import tensorflow as tf

with graph.as_default():   
    # Code layer
    code_input = tf.layers.flatten(inputs=conv_3)

    code_layer = tf.layers.dense(inputs=code_input,
                                 units=code_length,
                                 activation=tf.nn.sigmoid)

    code_mean = tf.reduce_mean(code_layer, axis=1)

DAG 的解码器部分如下：

import tensorflow as tf

with graph.as_default(): 
    # Decoder
    decoder_input = tf.reshape(code_layer, (-1, int(width / 2), int(height / 2), 1))

    convt_0 = tf.layers.conv2d_transpose(inputs=decoder_input,
                                         filters=128,
                                         kernel_size=(3, 3),
                                         strides=(2, 2),
                                         activation=tf.nn.relu,
                                         padding='same')

    convt_1 = tf.layers.conv2d_transpose(inputs=convt_0,
                                         filters=64,
                                         kernel_size=(3, 3),
                                         activation=tf.nn.relu,
                                         padding='same')

    convt_2 = tf.layers.conv2d_transpose(inputs=convt_1,
                                         filters=32,
                                         kernel_size=(3, 3),
                                         activation=tf.nn.relu,
                                         padding='same')

    convt_3 = tf.layers.conv2d_transpose(inputs=convt_2,
                                         filters=1,
                                         kernel_size=(3, 3),
                                         activation=tf.sigmoid,
                                         padding='same')

    output_images = tf.image.resize_images(convt_3, (X_train.shape[1], X_train.shape[2]), 
                                           method=tf.image.ResizeMethod.BICUBIC)

loss函数和 Adam 优化器在以下代码段中定义：

import tensorflow as tf

with graph.as_default():
    # Loss
    loss = tf.nn.l2_loss(convt_3 - input_images)

    # Training step
    training_step = tf.train.AdamOptimizer(0.001).minimize(loss)

一旦定义了完整的 DAG，我们就可以初始化会话和所有变量：

import tensorflow as tf

session = tf.InteractiveSession(graph=graph)
tf.global_variables_initializer().run()

一旦 TensorFlow 初始化，就可以开始训练过程，如下所示：

import numpy as np

for e in range(nb_epochs):
    np.random.shuffle(X_train)

    total_loss = 0.0
    code_means = []

    for i in range(0, X_train.shape[0] - batch_size, batch_size):
        X = np.expand_dims(X_train[i:i + batch_size, :, :], axis=3).astype(np.float32)

        _, n_loss, c_mean = session.run([training_step, loss, code_mean],
                                        feed_dict={
                                            input_images_xl: X
                                        })
        total_loss += n_loss
        code_means.append(c_mean)

    print('Epoch {}) Average loss per sample: {} (Code mean: {})'.
          format(e + 1, total_loss / float(X_train.shape[0]), np.mean(code_means)))

上一个代码段的输出如下：

Epoch 1) Average loss per sample: 11.933397521972656 (Code mean: 0.5420681238174438)
Epoch 2) Average loss per sample: 10.294102325439454 (Code mean: 0.4132006764411926)
Epoch 3) Average loss per sample: 9.917563934326171 (Code mean: 0.38105469942092896)
...
Epoch 600) Average loss per sample: 0.4635812330245972 (Code mean: 0.42368677258491516)

在训练过程结束时，每个样本的平均损失约为 0.46（考虑 32×32 图像），编码的平均值为 0.42。 该值表示编码相当密集，因为期望单个值在(0, 1)范围内均匀分布； 因此，平均值为 0.5。 在这种情况下，我们对这个数据不感兴趣，但是在寻找稀疏度时我们也将比较结果。

下图显示了一些样本图像的自编码器的输出：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yehDkYQZ-1681652675159)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/d73899a4-f6e4-4cfd-b283-8693a4428982.png)]

深度卷积自编码器的样本输出

扩大到 64×64 会部分影响重建的质量。 但是，通过降低压缩率和增加代码长度可以获得更好的结果。

去噪自编码器

自编码器的一个非常有用的应用并不严格取决于它们查找低维表示形式的能力，而是依赖于从输入到输出的转换过程。 特别地，我们假设一个零中心数据集X和一个嘈杂的版本，其样本具有以下结构：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AfBWJVGl-1681652675159)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/6b4e6663-04c2-47c6-af95-153f0cefa172.png)]

在这种情况下，自编码器的目标是消除噪声项并恢复原始样本x[i]。 从数学角度来看，标准和去噪自编码器之间没有特别的区别； 但是，重要的是要考虑此类模型的容量需求。 由于他们必须恢复原始样本，因此在输入受损（其特征占用更大的样本空间）的情况下，层的数量和大小可能比标准自编码器要大。 当然，考虑到复杂性，没有一些测试就不可能有清晰的洞察力。 因此，我强烈建议从较小的模型开始，然后增加容量，直到最佳成本函数达到合适的值为止。 为了增加噪音，有几种可能的策略：

• 破坏每个批量中的样本（贯穿整个周期）。
• 将噪声层用作编码器的输入 1。
• 将丢弃层用作编码器的输入 1（例如，椒盐噪声）。 在这种情况下，丢弃的概率可以是固定的，也可以以预定义的间隔（例如，（0.1，0.5））随机采样。

如果假定噪声为高斯噪声（这是最常见的选择），则可能会同时产生同调和异调噪声。 在第一种情况下，所有分量的方差都保持恒定（即n(i) ~ N(0, σ^2 I)），而在后一种情况下，每个组件具有其自身的差异。 根据问题的性质，另一种解决方案可能更合适。 但是，在没有限制的情况下，总是最好使用异方差噪声，以提高系统的整体鲁棒性。

给深度卷积自编码器增加噪声

在此示例中，我们将修改先前开发的深度卷积自编码器，以管理嘈杂的输入样本。 DAG 几乎等效，不同之处在于，现在我们需要同时提供噪点图像和原始图像：

import tensorflow as tf

with graph.as_default():
    input_images_xl = tf.placeholder(tf.float32, 
                                     shape=(None, X_train.shape[1], X_train.shape[2], 1))
    input_noisy_images_xl = tf.placeholder(tf.float32, 
                                           shape=(None, X_train.shape[1], X_train.shape[2], 1))

    input_images = tf.image.resize_images(input_images_xl, (width, height), 
                                          method=tf.image.ResizeMethod.BICUBIC)
    input_noisy_images = tf.image.resize_images(input_noisy_images_xl, (width, height), 
                                                method=tf.image.ResizeMethod.BICUBIC)

    # Encoder
    conv_0 = tf.layers.conv2d(inputs=input_noisy_images,
                              filters=16,
                              kernel_size=(3, 3),
                              strides=(2, 2),
                              activation=tf.nn.relu,
                              padding='same')
...

loss函数当然是通过考虑原始图像来计算的：

...

# Loss
loss = tf.nn.l2_loss(convt_3 - input_images)

# Training step
training_step = tf.train.AdamOptimizer(0.001).minimize(loss)

在变量的标准初始化之后，我们可以考虑附加噪声n[i] = N(0, 0.45)（即σ ≈ 0.2）开始训练过程：

import numpy as np

for e in range(nb_epochs):
    np.random.shuffle(X_train)

    total_loss = 0.0
    code_means = []

    for i in range(0, X_train.shape[0] - batch_size, batch_size):
        X = np.expand_dims(X_train[i:i + batch_size, :, :], axis=3).astype(np.float32)
        Xn = np.clip(X + np.random.normal(0.0, 0.2, size=(batch_size, X_train.shape[1], X_train.shape[2], 1)), 0.0, 1.0)

        _, n_loss, c_mean = session.run([training_step, loss, code_mean],
                                        feed_dict={
                                            input_images_xl: X,
                                            input_noisy_images_xl: Xn
                                        })
        total_loss += n_loss
        code_means.append(c_mean)

    print('Epoch {}) Average loss per sample: {} (Code mean: {})'.
          format(e + 1, total_loss / float(X_train.shape[0]), np.mean(code_means)))

一旦训练了模型，就可以用一些嘈杂的样本对其进行测试。 结果显示在以下屏幕截图中：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9H8jeEXE-1681652675160)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/34830da1-cd25-4d86-bcf2-da6dd16f5586.png)]

噪音样本（上排）； 去噪图像（下排）

如您所见，自编码器已经成功学习了如何对输入图像进行去噪，即使它们已经损坏。 我邀请您与其他数据集一起测试模型，以寻找允许合理良好重构的最大噪声方差。

稀疏自编码器

标准自编码器生成的代码通常很密集； 但是，如第 7 章，“降维和成分分析”中所讨论的，有时，最好使用字典过于完整和稀疏编码。 实现此目标的主要策略是简单地在成本函数上添加L[1]罚款（在代码层上）：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SwvTyrbv-1681652675160)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/ec6a414d-389c-457f-9944-ba198988bf14.png)]

α常数确定将要达到的稀疏程度。 当然，由于C[s]的最佳值与原始值不对应，因此，为了达到相同的精度，通常需要更多的周期和更长的代码层。 由 Andrew Ng（斯坦福大学的 CS294A “稀疏自编码器”）提出的另一种方法是基于稍微不同的方法。 代码层被认为是一组独立的伯努利随机变量。 因此，给定另一组均值较小的伯努利变量（例如p[r] ~ B(0.05)），就有可能尝试找到使代码最小化的最佳代码z[i]与此类参考分布之间的 Kullback-Leibler 散度：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jWzkUltF-1681652675160)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/04ada51f-118c-4cd8-8c62-f1ca4ec0b792.png)]

因此，新的成本函数变为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fjojqrEk-1681652675160)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/f27a0c44-85f3-4b2f-accc-796d9b3c7e98.png)]

最终效果与使用L[1]惩罚所获得的效果没有太大不同。 实际上，在这两种情况下，模型都被迫学习次优表示，还试图最小化目标（如果单独考虑）将导致输出代码始终为空。 因此，全部成本函数将达到最小，从而保证重构能力和稀疏性（必须始终与代码长度保持平衡）。 因此，通常，代码越长，可以实现的稀疏度就越大。

向深度卷积自编码器添加稀疏约束

在此示例中，我们想通过使用L[1]罚分来提高代码的稀疏性。 DAG 和训练过程与主要示例完全相同，唯一的区别是loss函数，现在变为：

...
sparsity_constraint = 0.01 * tf.reduce_sum(tf.norm(code_layer, ord=1, axis=1))
loss = tf.nn.l2_loss(convt_3 - input_images) + sparsity_constraint
...

我们添加了α = 0.01的稀疏约束； 因此，我们可以通过检查平均代码长度来重新训练模型。 该过程的输出如下：

Epoch 1) Average loss per sample: 12.785746307373048 (Code mean: 0.30300647020339966)
Epoch 2) Average loss per sample: 10.576686706542969 (Code mean: 0.16661183536052704)
Epoch 3) Average loss per sample: 10.204148864746093 (Code mean: 0.15442773699760437)
...
Epoch 600) Average loss per sample: 0.8058895015716553 (Code mean: 0.028538944199681282)

如您所见，代码现在变得极为稀疏，最终均值大约等于 0.03。 该信息表明大多数代码值接近于零，并且在解码图像时只能考虑其中的几个。 作为练习，我邀请您分析一组选定图像的代码，尝试根据它们的激活/不激活来理解其值的语义。

变分自编码器

让我们考虑从数据生成过程中提取的数据集X，p_data。 可变自编码器是一种生成模型（基于标准自编码器的主要概念），由 Kingma 和 Welling 提出（在《贝叶斯变分自编码》），旨在再现数据生成过程。 为了实现此目标，我们需要从基于一组潜在变量z和一组可学习参数θ的通用模型开始。 给定样本x[i] ∈ X，该模型的概率为p(x, z; θ) 。 因此，训练过程的目标是找到使似然性最大化的最佳参数p(x; θ)，该参数可以通过边缘化整个联合概率来获得：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-U02whbP4-1681652675161)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/cc7c4316-bf98-4ae0-b3bd-09a2f5239ad6.png)]

以前的表达式很简单，但是不幸的是，它很难以封闭形式处理。 主要原因是我们没有关于先验p(z; θ)的有效信息。 此外，即使假设例如z ~ N(0, Σ)（例如N(0, I)），找到有效样本的概率也非常稀疏 。 换句话说，给定z值，我们也不太可能生成实际上属于p_data的样本。 为了解决这个问题，作者提出了一种变分方法，我们将简要介绍一下（上述论文中有完整的解释）。 假设标准自编码器的结构，我们可以通过将编码器建模为q(z | x; θ[q])来引入代理参数化分布。 此时，我们可以计算q(·)与实际条件概率p(z | x; θ)之间的 Kullback-Leibler 散度

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uXKVlOqa-1681652675161)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/eaf4410d-472c-4bf6-8cb2-7d5839d84741.png)]

当期望值运算符在z上工作时，可以提取最后一项并将其移到表达式的左侧，变为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4ODDrDAW-1681652675161)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/cdaa12bb-4d9e-44f3-84f2-5cbc8bf78189.png)]

经过另一种简单的操作，先前的等式变为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BiCNQyNJ-1681652675161)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/56fb3b12-7f9b-4028-bb8d-116c18a81409.png)]

左侧是模型下样本的对数似然，而右侧是非负项（KL 散度）和另一个称为证据下界（ELBO）：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sOSeGsIV-1681652675161)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/8f1e8ea7-da26-4a01-9ca8-27e38f809cfa.png)]

正如我们将要讨论的，使用 ELBO 比处理公式的其余部分要容易得多，并且由于 KL 散度不会产生负面影响，所以如果我们最大化 ELBO，我们也将最大化对数似然率。

我们先前定义了p(z; θ) = N(0, I); 因此，我们可以将q(z | x; θ)建模为多元高斯模型，其中两个参数集（均值向量和协方差矩阵）由拆分概率编码器表示。 特别是，给定样本x，编码器现在必须同时输出平均向量μ(z | x; θ[q])和协方差矩阵Σ(z | x; θ[q])。 为简单起见，我们可以假设矩阵是对角线，因此两个组件的结构完全相同。 结果分布为q(​​z | x; θ[q]) = N(μ(z | x; θ[q]), Σ(z | x; θ[q]); 因此，ELBO 的第一项是两个高斯分布之间的负 KL 散度：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LDjPm1ai-1681652675162)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/30ba70c1-c5f3-4ea6-b019-0e51ab9b72ad.png)]

在前面的公式中，p是代码长度，因此它是均值和对角协方差向量的维数。 右侧的表达式非常容易计算，因为Σ是对角线的（也就是说，迹线是元素的总和，行列式是乘积）。 但是，当使用随机梯度下降（SGD）算法时，此公式的最大值尽管正确，但却不是可微的运算。 为了克服这个问题，作者建议重新分配分布。

当提供一批时，对正态分布进行采样，获得α ~ N(0, I)。 使用该值，可以使用概率编码器的输出来构建所需的样本：μ(z | x; θ[q]) + α • ∑(z | x; θ[q])^2。 该表达式是可微的，因为α在每个批量中都是常数（当然，就像μ(z | x; θ[q])和∑(z | x; θ[q])用神经网络参数化，它们是可微的）。

ELBO 右侧的第二项是log p(x|z; θ)的期望值。 不难看出，这样的表达式与原始分布和重构之间的交叉熵相对应：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-38CSInId-1681652675162)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/443c5d4e-8661-4887-a98e-e6fe63f6ad03.png)]

这是标准自编码器的成本函数，在使用伯努利分布的假设下，我们将其最小化。 因此，公式变为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6gVMA5eP-1681652675162)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/f91ac945-2781-4c3f-8049-27d941e1f336.png)]

深度卷积变分自编码器的示例

在此示例中，我们要基于 Olivetti 人脸数据集构建和训练深度卷积变分自编码器。 该结构与我们第一个示例中使用的结构非常相似。 编码器具有以下几层：

• 具有 163×3过滤器，2×2步幅，ReLU 激活和相同填充的 2D 卷积
• 具有 32 个3×3过滤器，1×1步幅，ReLU 激活和相同的填充的 2D 卷积
• 具有 64 个3×3过滤器，1×1跨距，ReLU 激活和相同的填充的 2D 卷积
• 2D 卷积，具有 1283×3个过滤器，1×1跨距，ReLU 激活和相同的填充

解码器具有以下转置卷积：

• 2D 转置卷积，具有 1283×3个过滤器，2×2步幅，ReLU 激活和相同的填充
• 2D 转置卷积，具有 1283×3个过滤器，2×2步幅，ReLU 激活和相同的填充
• 具有 32 个3×3过滤器，1×1跨距，ReLU 激活和相同填充的 2D 转置卷积
• 2D 转置卷积，带有 13×3过滤器，1×1步幅，Sigmoid 激活，以及相同的填充

TensorFlow 完全控制了噪声的产生，并且基于理论部分中说明的技巧。 以下代码段显示了 DAG 的第一部分，其中包含图定义和编码器：

import tensorflow as tf

nb_epochs = 800
batch_size = 100
code_length = 512
width = 32
height = 32

graph = tf.Graph()

with graph.as_default():
    input_images_xl = tf.placeholder(tf.float32, 
                                     shape=(batch_size, X_train.shape[1], X_train.shape[2], 1))
    input_images = tf.image.resize_images(input_images_xl, (width, height), 
                                          method=tf.image.ResizeMethod.BICUBIC)

    # Encoder
    conv_0 = tf.layers.conv2d(inputs=input_images,
                              filters=16,
                              kernel_size=(3, 3),
                              strides=(2, 2),
                              activation=tf.nn.relu,
                              padding='same')

    conv_1 = tf.layers.conv2d(inputs=conv_0,
                              filters=32,
                              kernel_size=(3, 3),
                              activation=tf.nn.relu,
                              padding='same')

    conv_2 = tf.layers.conv2d(inputs=conv_1,
                              filters=64,
                              kernel_size=(3, 3),
                              activation=tf.nn.relu,
                              padding='same')

    conv_3 = tf.layers.conv2d(inputs=conv_2,
                              filters=128,
                              kernel_size=(3, 3),
                              activation=tf.nn.relu,
                              padding='same')

DAG 中定义代码层的部分如下：

import tensorflow as tf

with graph.as_default():
    # Code layer
    code_input = tf.layers.flatten(inputs=conv_3)

    code_mean = tf.layers.dense(inputs=code_input,
                                units=width * height)

    code_log_variance = tf.layers.dense(inputs=code_input,
                                        units=width * height)

    code_std = tf.sqrt(tf.exp(code_log_variance))

DAG 的解码器部分如下：

import tensorflow as tf

with graph.as_default():  
    # Decoder
    decoder_input = tf.reshape(sampled_code, (-1, int(width / 4), int(height / 4), 16))

    convt_0 = tf.layers.conv2d_transpose(inputs=decoder_input,
                                         filters=128,
                                         kernel_size=(3, 3),
                                         strides=(2, 2),
                                         activation=tf.nn.relu,
                                         padding='same')

    convt_1 = tf.layers.conv2d_transpose(inputs=convt_0,
                                         filters=128,
                                         kernel_size=(3, 3),
                                         strides=(2, 2),
                                         activation=tf.nn.relu,
                                         padding='same')

    convt_2 = tf.layers.conv2d_transpose(inputs=convt_1,
                                         filters=32,
                                         kernel_size=(3, 3),
                                         activation=tf.nn.relu,
                                         padding='same')

    convt_3 = tf.layers.conv2d_transpose(inputs=convt_2,
                                         filters=1,
                                         kernel_size=(3, 3),
                                         padding='same')

    convt_output = tf.nn.sigmoid(convt_3)

    output_images = tf.image.resize_images(convt_output, (X_train.shape[1], X_train.shape[2]), 
                                           method=tf.image.ResizeMethod.BICUBIC)

DAG 的最后一部分包含损失函数和 Adam 优化器，如下所示：

import tensorflow as tf

with graph.as_default():
    # Loss
    reconstruction = tf.nn.sigmoid_cross_entropy_with_logits(logits=convt_3, labels=input_images)
    kl_divergence = 0.5 * tf.reduce_sum(
            tf.square(code_mean) + tf.square(code_std) - tf.log(1e-8 + tf.square(code_std)) - 1, axis=1)

    loss = tf.reduce_sum(tf.reduce_sum(reconstruction) + kl_divergence)

    # Training step
    training_step = tf.train.AdamOptimizer(0.001).minimize(loss)

损失函数由两个部分组成：

1. 基于交叉熵的重构损失
2. 代码分布与参考正态分布之间的 Kullback-Leibler 散度

在这一点上，像往常一样，我们可以初始化会话和所有变量，并开始每批 800 个周期和 100 个样本的训练过程：

import tensorflow as tf
import numpy as np

session = tf.InteractiveSession(graph=graph)
tf.global_variables_initializer().run()

for e in range(nb_epochs):
    np.random.shuffle(X_train)

    total_loss = 0.0

    for i in range(0, X_train.shape[0] - batch_size, batch_size):
        X = np.zeros((batch_size, 64, 64, 1), dtype=np.float32)
        X[:, :, :, 0] = X_train[i:i + batch_size, :, :]

        _, n_loss = session.run([training_step, loss],
                                feed_dict={
                                    input_images_xl: X
                                })
        total_loss += n_loss

    print('Epoch {}) Average loss per sample: {}'.format(e + 1, total_loss / float(batch_size)))

在训练过程的最后，我们可以测试几个样本的重构。 结果显示在以下屏幕截图中：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ywDZC8os-1681652675162)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/61c66921-ed45-412b-99e1-4161ff2da04e.png)]

变分自编码器产生的样本重构

作为练习，我邀请读者修改 DAG，以接受通用输入代码并评估模型的生成属性。 或者，可以获取训练样本的代码并施加一些噪声，以便观察对输出重构的影响。

基于 Hebbian 的主成分分析

在本节中，我们将分析两个神经模型（Sanger 和 Rubner-Tavan 网络），它们可以执行主成分分析（PCA），而无需对协方差矩阵进行特征分解或执行截断的 SVD。 它们都是基于 Hebbian 学习的概念（有关更多详细信息，请参阅《理论神经科学》），这是有关非常简单的神经元动力学的第一批数学理论之一。 然而，这些概念具有非常有趣的含义，尤其是在组件分析领域。 为了更好地了解网络的动力学，提供神经元基本模型的快速概述将很有帮助。 让我们考虑一个输入x ∈ R^n和权重向量w ∈ ℜ^n。 神经元执行点积（无偏差），以产生标量输出y：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MLgJ63Yn-1681652675162)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/82b33ae4-637c-4004-b89b-c6e72863705d.png)]

现在，如果我们想象两个神经元，第一个被称为突触前单元，另一个被称为突触后单元。 Hebbian 规则指出，当突触前​​和突触后单元都输出具有相同符号（尤其是正值）的值时，突触强度必须增加，而当符号不同时，突触强度必须减弱。 这种概念的数学表达式如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JsPs2GoC-1681652675163)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/d422484d-1407-4fbe-8258-bb66809bb7be.png)]

常数η是学习率。 完整的分析超出了本书的范围，但是有可能证明，一个 Hebbian 神经元（经过一些非常简单的修改，需要控制w的生长）可以改变突触的权重，因此在足够多的迭代之后，它沿着数据集的第一个主成分X对齐。 从这个结果（我们不会证明）开始，我们可以介绍 Sanger 网络。

Sanger 网络

Sanger 网络模型由 Sanger 提出（在《单层线性前馈神经网络中的最佳无监督学习》），以便提取第一个数据集的X的k个主成分，以在线过程降序排列（相反，标准 PCA 是需要整个数据集的批量）。 即使有基于特定版本 SVD 的增量算法，这些神经模型的主要优点是它们处理单个样本的固有能力而不会损失任何表现。 在显示网络结构之前，有必要对 Hebb 规则进行修改，称为 Oja 规则：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LDgCb8FJ-1681652675163)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/eb954467-be52-42bb-a06d-e3d8cd62dd8c.png)]

引入此规则是为了解决标准 Hebbian 神经元无限增长的问题。 实际上，很容易理解，如果点积w^T x为正，Δw 将通过增加w的幅度来更新权重。 和更多。 因此，在进行大量迭代之后，模型可能会遇到溢出。 奥雅定律通过引入一种自动限制来克服这个问题，该自动限制迫使权重幅度饱和而不影响神经元找到第一个主要成分的方向的能力。 实际上，用w[k]表示第k次迭代之后的权重向量，可以证明以下内容：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BOxP45uF-1681652675163)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/09e7fdb7-16a9-4ec9-87ba-717623f9c860.png)]

Sanger 网络基于 Oja 规则的修改版本，该规则定义为广义 Hebbian 学习（GHL）。 假设我们有一个数据集X，包含m个向量，x[i] ∈ R^n。 下图显示了网络的结构：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aItFf1kc-1681652675163)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/f212e875-6028-405a-a901-657d01e39d7e.png)]

通用 Sanger 网络的结构

权重被组织成一个矩阵，W = {w[ij]}（w[ij]是连接突触前单元的权重 ，i，带有突触后单元，j）； 因此，可以使用以下公式来计算输出的激活：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EfeSrEQp-1681652675163)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/e021d025-55ed-4793-b6d9-b8cec5b50302.png)]

但是，在这种网络中，我们对最终权重更感兴趣，因为它们必须等于第一个n主分量。 不幸的是，如果我们应用 Oja 规则而不做任何修改，则所有神经元都将找到相同的组件（第一个组件）。 因此，必须采用不同的策略。 从理论上讲，我们知道主成分必须正交。 因此，如果w[1]是具有第一个分量方向的向量，则可以强制w[2]正交于w[1]，依此类推。 该方法基于 Gram-Schmidt 正交归一化程序。 让我们考虑两个向量-已经收敛的w[1]，和w[20]， 任何干预措施，也将收敛于w[1]。 通过考虑此向量在w[1]上的投影，可以找到w[20]的正交分量：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-D5N2maeY-1681652675164)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/67503a88-e4d1-468e-8b90-6d874d81a731.png)]

此时，w[2]的正交分量等于：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-otQyny6C-1681652675164)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/eb256bb9-cc11-492f-b9b7-5a0d54799d6a.png)]

第三部分必须正交于w[1]和w[2]，因此必须对所有n个单元，直到最终收敛。 而且，我们现在正在使用已经融合的组件，而是使用并行更新的动态系统。 因此，有必要将此程序纳入学习规则，如下所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DViSaSTR-1681652675164)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/350f6137-1ddd-447d-879a-79de245a6115.png)]

在给定输入x的情况下，先前的更新是指单个权重w[ij]。 容易理解，第一部分是标准 Hebbian 法则，而其余部分是正交项，它扩展到y[i]之前的所有单元。

以矩阵形式，更新内容如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wOvejq2v-1681652675164)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/9aa37ec6-8cf8-4828-a845-ec719720409a.png)]

Tril(·)函数计算方阵的下三角部分。 收敛性证明并非无关紧要，但在η单调减少的温和条件下，可以看到该模型如何以降序收敛到第一个n主成分。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jHbMSsJY-1681652675169)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/9493c073-860c-40de-a254-d938060914d8.png)]

这样的约束并不难实现。 但是，一般来说，当η < 1并在迭代过程中保持恒定时，该算法也可以达到收敛。

Sanger 网络的一个例子

让我们考虑一个使用 scikit-learn make_blobs() 实用函数获得的样本二维零中心数据集：

import numpy as np

def zero_center(Xd):
    return Xd - np.mean(Xd, axis=0)

X, _ = make_blobs(n_samples=500, centers=3, cluster_std=[5.0, 1.0, 2.5], random_state=1000)
Xs = zero_center(X)

Q = np.cov(Xs.T)
eigu, eigv = np.linalg.eig(Q)

print('Covariance matrix: {}'.format(Q))
print('Eigenvalues: {}'.format(eigu))
print('Eigenvectors: {}'.format(eigv.T))

上一个代码段的输出如下：

Covariance matrix: [[18.14296606  8.15571356]
 [ 8.15571356 22.87011239]]
Eigenvalues: [12.01524122 28.99783723]
Eigenvectors: [[-0.79948496  0.60068611]
 [-0.60068611 -0.79948496]]

特征值分别约为 12 和 29，，表示第一主成分（对应于转置特征向量矩阵的第一行，因此(-0.799, 0.6)比第二个要短得多。 当然，在这种情况下，我们已经通过对协方差矩阵进行特征分解来计算了主成分，但这只是出于教学目的。 Sanger 网络将按降序提取组件； 因此，我们期望找到第二列作为权重矩阵的第一列，第一列作为权重矩阵的第二列。 让我们从初始化权重和训练常数开始：

import numpy as np

n_components = 2
learning_rate = 0.01
nb_iterations = 5000
t = 0.0

W_sanger = np.random.normal(scale=0.5, size=(n_components, Xs.shape[1]))
W_sanger /= np.linalg.norm(W_sanger, axis=1).reshape((n_components, 1))

In order to reproduce the example, it’s necessary to set the random seed equal to 1,000; that is, np.random.seed(1000).

在这种情况下，我们将执行固定的迭代次数（5,000）； 但是，我邀请您修改示例，以基于在随后两个时间步长计算出的权重之间的差的范数（例如 Frobenius）采用公差和停止准则（此方法可以加快训练速度） 避免无用的迭代）。

下图显示了初始配置：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kIW48L1N-1681652675170)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/c7b2575f-cea3-421c-9b03-33002dd0c053.png)]

Sanger 网络的初始配置

此时，我们可以开始训练周期，如下所示：

import numpy as np

for i in range(nb_iterations):
    dw = np.zeros((n_components, Xs.shape[1]))
    t += 1.0

    for j in range(Xs.shape[0]):
        Ysj = np.dot(W_sanger, Xs[j]).reshape((n_components, 1))
        QYd = np.tril(np.dot(Ysj, Ysj.T))
        dw += np.dot(Ysj, Xs[j].reshape((1, X.shape[1]))) - np.dot(QYd, W_sanger)

    W_sanger += (learning_rate / t) * dw
    W_sanger /= np.linalg.norm(W_sanger, axis=1).reshape((n_components, 1))

print('Final weights: {}'.format(W_sanger))
print('Final covariance matrix: {}'.format(np.cov(np.dot(Xs, W_sanger.T).T)))

上一个代码段的输出如下：

Final weights: [[-0.60068611 -0.79948496]
 [-0.79948496  0.60068611]]
Final covariance matrix: [[ 2.89978372e+01 -2.31873305e-13]  
 [-2.31873305e-13 1.20152412e+01]]

如您所见，最终的协方差矩阵如预期的那样是去相关的，并且权重已收敛到C的特征向量。 权重（主要成分）的最终配置如下图所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NGH6iB9w-1681652675170)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/b50469af-2fc0-4dc7-97d2-5a58cc89c050.png)]

Sanger 网络的最终配置

第一个主成分对应的权重是w[0]，它是最大的，而w[1]是第二个成分。 我邀请您使用高维数据集测试网络，并根据协方差矩阵的 SVD 或本征分解将表现与标准算法进行比较。

Rubner-Attic 网络

Rubner 和 Tavan 提出了另一种可以执行 PCA 的神经网络（在《主成分分析的自组织网络》）。 但是，他们的方法基于协方差矩阵的去相关，这是 PCA 的最终结果（也就是说，就像使用自下而上的策略，而标准过程是自上而下的操作一样）。 让我们考虑一个零中心数据集X和一个网络，其输出为y ∈ R^m向量。 因此，输出分布的协方差矩阵如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vgaXYbDK-1681652675170)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/0a6cd2b9-0661-43cb-baeb-186e98dbda5e.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oHqQHWco-1681652675171)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/5e068665-3ed9-41b4-8e70-9b2a4e768718.png)]

通用 Rubner-Tavan 网络的结构

如您所见，与 Sanger 网络的主要区别在于每个输出单元（第一个输出单元除外）之前都存在求和节点。 这种方法称为分层横向连接，因为每个节点y[i] (i > 0)由直接组件n[i]组成，加到所有先前的加权输出中。 因此，假设使用v^(i)表示法，以表示向量的第i个分量，网络输出如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BkNqw7YG-1681652675171)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/28b97b62-ca15-49e7-9117-686e2f01f49b.png)]

已经证明，具有特定权重更新规则（我们将要讨论）的该模型收敛到单个稳定的固定点，并且输出被迫变得相互解相关。 查看模型的结构，操作顺序如下：

• 第一个输出保持不变
• 第二个输出被强制与第一个输出去相关
• 第三输出被强制与第一输出和第二输出去相关，依此类推
• 最后的输出被强制与所有先前的输出去相关

经过多次迭代后，每个生成的y[i] y[j]以及i ≠ j都为空，而C变成对角协方差矩阵。 此外，在上述论文中，作者证明了特征值（对应于方差）是按降序排序的； 因此，可以通过选择包含前p行和列的子矩阵来选择顶部的p组件。

通过使用两个不同的规则（每个权重层一个）来更新 Rubner-Tavan 网络。 内部权重w[ij]通过使用 Oja 规则进行更新：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ad0O0DBC-1681652675171)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/efcc2114-ef49-40d9-a8b3-bd829d2487c1.png)]

该规则确保提取主成分时不会无限增长w[ij]。 相反，外部权重v[jk]通过使用反希伯来规则更新：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-p3xnMs0f-1681652675171)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/03eed34d-9192-4583-a97f-86ed71c4cb4d.png)]

前一个公式的第一项-ηy^(j) y^(k))负责解相关，而第二项类似于 Oja’s 规则，用作防止权重溢出的自限制正则器。 特别地，-ηy(i) y^(k)项可以解释为更新规则的反馈信号w[ij]，它受w[ij]项校正的实际输出的影响。 考虑到 Sanger 网络的行为，不容易理解，一旦输出去相关，内部权重w[ij]就变成正交，代表第一个主要成分X。

以矩阵形式，权重w[ij]可以立即排列为W = {w[ij]}，这样在训练过程结束时，每一列都是C的特征向量（降序排列）。 相反，对于外部权重v[jk]，我们需要再次使用Tril(·)运算符：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9GQ3kPco-1681652675171)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/9080b2af-6409-4238-a6a8-8f230792ce22.png)]

因此，迭代t + 1的输出变为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9t4rVZHJ-1681652675172)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/2868e72f-7437-444e-94e3-4c2068388a47.png)]

有趣的是，这样的网络经常输出。 因此，一旦应用了输入，就需要进行几次迭代才能使y稳定下来（理想情况下，更新必须持续到||y^(t + 1) - y^(t)|| → 0）。

Rubner-Tavan 网络的一个例子

在此示例中，我们将使用 Sanger 网络示例中定义的数据集，以便使用 Rubner-Tavan 网络进行主成分提取。 为了方便起见，让我们重新计算特征分解：

import numpy as np

Q = np.cov(Xs.T)
eigu, eigv = np.linalg.eig(Q)

print('Eigenvalues: {}'.format(eigu))
print('Eigenvectors: {}'.format(eigv.T))

上一个代码段的输出如下：

Eigenvalues: [12.01524122 28.99783723]
Eigenvectors: [[-0.79948496 0.60068611]
 [-0.60068611 -0.79948496]]

现在，我们可以初始化超参数，如下所示：

n_components = 2 learning_rate = 0.0001 max_iterations = 1000 stabilization_cycles = 5 threshold = 0.00001 W = np.random.normal(0.0, 0.5, size=(Xs.shape[1], n_components))
V = np.tril(np.random.normal(0.0, 0.01, size=(n_components, n_components)))
np.fill_diagonal(V, 0.0)

prev_W = np.zeros((Xs.shape[1], n_components))
t = 0

因此，我们选择采用等于 0.00001 的停止阈值（比较基于权重矩阵的两次连续计算的 Frobenius 范数）和最多 1,000 次迭代。 我们还设置了五个稳定周期和固定的学习率η = 0.0001。 我们可以开始学习过程，如下所示：

import numpy as np

while np.linalg.norm(W - prev_W, ord='fro') > threshold and t < max_iterations:
    prev_W = W.copy()
    t += 1    for i in range(Xs.shape[0]):
        y_p = np.zeros((n_components, 1))
        xi = np.expand_dims(Xs[i], 1)
        y = None   for _ in range(stabilization_cycles):
            y = np.dot(W.T, xi) + np.dot(V, y_p)
            y_p = y.copy()

        dW = np.zeros((Xs.shape[1], n_components))
        dV = np.zeros((n_components, n_components))

        for t in range(n_components):
            y2 = np.power(y[t], 2)
            dW[:, t] = np.squeeze((y[t] * xi) + (y2 * np.expand_dims(W[:, t], 1)))
            dV[t, :] = -np.squeeze((y[t] * y) + (y2 * np.expand_dims(V[t, :], 1)))

        W += (learning_rate * dW)
        V += (learning_rate * dV)

        V = np.tril(V)
        np.fill_diagonal(V, 0.0)

        W /= np.linalg.norm(W, axis=0).reshape((1, n_components))

print('Final weights: {}'.format(W))

前一个块的输出如下：

Final weights: [[-0.60814345 -0.80365858]
 [-0.79382715 0.59509065]]

如预期的那样，权重收敛到协方差矩阵的特征向量。 我们还计算最终的协方差矩阵，以检查其值：

import numpy as np

Y_comp = np.zeros((Xs.shape[0], n_components))

for i in range(Xs.shape[0]):
    y_p = np.zeros((n_components, 1))
    xi = np.expand_dims(Xs[i], 1)

    for _ in range(stabilization_cycles):
        Y_comp[i] = np.squeeze(np.dot(W.T, xi) + np.dot(V.T, y_p))
        y_p = y.copy()

print('Final covariance matrix: {}'.format(np.cov(Y_comp.T)))

输出如下：

Final covariance matrix: [[28.9963492 0.31487817]
 [ 0.31487817 12.01606874]]

同样，最终协方差矩阵是去相关的（误差可忽略不计）。 Rubner-Tavan 的网络通常比 Sanger 网络快，这是因为反希伯来语的反馈加快了收敛速度。 因此，当采用这种模型时，它们应该是首选。 但是，调整学习率非常重要，这样可以避免振荡。 我建议从一个较小的值开始，然后稍微增加它，直到迭代次数达到最小值为止。 另外，也可以从较高的学习率入手，以便更快地进行初始校正，并可以通过使用线性（如 Sanger 网络）或指数衰减逐步降低学习率。

无监督的深度信念网络

在本节中，我们将讨论一个非常著名的生成模型，该模型可以在无监督的情况下使用，以执行从预定义的数据生成过程中提取的输入数据集X的降维。 由于本书没有特定的先决条件，并且数学上的复杂度很高，因此我们将简要介绍这些概念，而无需提供证明，也不会对算法的结构进行深入分析。 在讨论深度信念网络（DBN）之前，有必要介绍另一种模型受限玻尔兹曼机（RBM）， 被视为 DBN 的构建块。

受限玻尔兹曼机

在《动态系统的信息处理：谐波理论的基础》中，提出了这个网络作为概率生成模型，也称为 Harmonium。 换句话说，RBM 的目标是学习未知分布（即数据生成过程），以便生成所有可能的样本。 下图显示了通用结构：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Fl7yozbE-1681652675172)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/6f0f4654-5cfe-4dc4-b79b-606c14a2ec71.png)]

通用受限玻尔兹曼机的结构

神经元x[i]是可观察到的（也就是说，它们代表 RBM 必须学习的过程生成的向量），而h[j]是潜在的（也就是说，它们是隐藏的并且有助于x[i]假定的值）。 由于没有任何进一步的细节，我们需要说这个模型具有马尔科夫随机场（MRF）的结构，这是由于相同层的神经元之间没有连接（即描述网络的图是二分图）。 MRF 的一个重要特性是可以用吉布斯分布对整个联合概率p(x, h; θ)进行建模：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-r0m2YPBH-1681652675172)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/c997f7bc-603a-4fd5-8bdf-6ab3fad3a30c.png)]

指数E(x, h, θ)发挥物理系统能量的作用，在我们的情况下，它等于：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3VH6MKW1-1681652675172)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/fec60140-16e2-454b-a5dd-61909bce0d08.png)]

该公式的主要假设是所有神经元都是伯努利分布的（即x[i], h[j] ~ B(0, 1)） 项b[i]和c[j]是可观察和潜在单位的偏差。 给定数据生成过程p_data，必须优化 RBM，以便p(x; θ)的可能性最大化。 跳过所有中间步骤（可以在前面的文章中找到），可以证明以下几点：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ppaSWkHn-1681652675173)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/e1cdc672-50a0-425c-8811-603832e1b5dd.png)]

在先前的公式中，$1是 Sigmoid 函数。 给定这两个表达式，可以得出（省略操作）对数似然率相对于所有可学习变量的梯度：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jd44giQz-1681652675173)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/145060cb-3837-4aa0-922f-ec99defbc34a.png)]

很容易理解，所有梯度的第一项都非常容易计算，而所有第二项都需要所有可能的可观测值之和。 这显然是一个棘手的问题，无法以封闭的形式解决。 因此，Hinton（训练受限的玻尔兹曼机器的实用指南》）提出了一种名为对比发散的算法 ，可用于查找近似解。 对这种方法的解释需要了解马尔可夫链（这不是前提条件）。 但是，我们可以概括地说该策略是通过有限（少量）采样步骤（通常，一个步骤就足以获得良好的结果）来计算梯度的近似值。 这种方法可以非常有效地训练 RBM，并使深层信念网络易于使用并且非常有效。

深度信念网络

DBN 是基于 RBM 的堆叠模型。 下图显示了通用结构：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pTBD8Klu-1681652675173)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/283459b4-8a2a-418c-98a0-128affb35d4b.png)]

通用 DBN 的结构

第一层包含可见单元，其余所有单元都是潜在单元。 在无监督的情况下，目标是学习未知分布，找出样本的内部表示。 实际上，当潜在单元的数量少于输入单元的数量时，模型将学习如何使用低维子空间对分布进行编码。 Hinton 和 Osindero（在《深层信念网络的快速学习算法》）提出了逐步贪婪训练程序（这是通常执行的程序）。 每对层都被认为是 RBM，并使用对比发散算法进行训练。 一旦对 RBM 进行了训练，则隐藏层将成为后续 RBM 的可观察层，并且该过程将一直持续到最后一个。 因此，DBN 开发了一系列内部表示形式（这就是为什么将其定义为深度网络的原因），其中每个级别都接受了较低级别特征的训练。 该过程与可变自编码器并无不同。 但是，在这种情况下，模型的结构更加僵化（例如，无法使用卷积单元）。 而且，输出不是输入的重建，而是内部表示。 因此，考虑上一节中讨论的公式，如果有必要反转过程（即给定内部表示，获得输入），则必须使用以下公式从最顶层进行采样：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FyuvwdR6-1681652675173)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/ee120b1c-ad77-481c-9f39-0d90a1f6c72c.png)]

当然，必须向后重复此过程，直到到达实际的输入层为止。 DBN 非常强大（例如，在天体物理学领域有一些科学应用），即使它们的结构不像其他更新的模型那样灵活。 但是，复杂度通常较高，因此，我总是建议从较小的模型开始，仅在最终精度不足以满足特定目的的情况下才增加层和/或神经元的数量。

无监督 DBN 的示例

在此示例中，我们要使用 DBN 来查找 MNIST 数据集的低维表示。 由于这些模型的复杂性很容易增加，我们将限制该过程为 500 个随机样本。 该实现基于 Deep-belief-network 包，该包同时支持 NumPy 和 TensorFlow。 在前一种情况下，必须从dbn包中导入类（其名称保持不变），而在后一种情况下，必须是dbn.tensorflow包。 在此示例中，我们将使用要求较少的 NumPy 版本，但也请读者检查 TensorFlow 版本。

让我们从加载和规范化数据集开始，如下所示：

import numpy as np

from sklearn.datasets import load_digits
from sklearn.utils import shuffle

nb_samples = 500

digits = load_digits()

X_train = digits['data'] / np.max(digits['data'])
Y_train = digits['target']

X_train, Y_train = shuffle(X_train, Y_train, random_state=1000)
X_train = X_train[0:nb_samples]
Y_train = Y_train[0:nb_samples]

现在，我们可以使用以下结构实例化UnsupervisedDBN类：

1. 64 个输入神经元（从数据集中隐式检测到）
2. 32 个 Sigmoid 神经元
3. 32 个 Sigmoid 神经元
4. 16 个 Sigmoid 神经元

因此，最后一个表示形式由 16 个值（原始大小的四分之一）组成。 我们将η = 0.025的学习率设置为每批 16 个样本（当然，我们邀请您检查其他配置，以最大程度地减少重构误差）。 以下代码段初始化并训练模型：

from dbn import UnsupervisedDBN

unsupervised_dbn = UnsupervisedDBN(hidden_layers_structure=[32, 32, 16],
                                   learning_rate_rbm=0.025,
                                   n_epochs_rbm=500,
                                   batch_size=16,
                                   activation_function='sigmoid')

X_dbn = unsupervised_dbn.fit_transform(X_train)

在训练过程的最后，我们可以将分布投影到二维空间上，然后分析分布。 像往常一样，我们将采用 t-SNE 算法，该算法可确保找到最相似的低维分布：

from sklearn.manifold import TSNE

tsne = TSNE(n_components=2, perplexity=10, random_state=1000)
X_tsne = tsne.fit_transform(X_dbn)

下图显示了投影样本的图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oL3jYTWn-1681652675173)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/359d9068-dc6b-45f6-bf32-e6c4ff19cc1f.png)]

无监督 DBN 输出表示的 t-SNE 图

如您所见，大多数块都具有很强的凝聚力，这表明数字的特殊属性已在较低维空间中成功表示。 在某些情况下，相同的数字组被划分为更多的群集，但是总的来说，噪点（隔离点）的数量非常少。 例如，包含数字2的组用符号x表示。 大部分样本在0 < x[0] < 30，x[1] < -40范围内； 但是，一个子组也位于-10 < x[1] < 10范围内。 如果我们检查这个小集群的邻居，它们是由代表数字8（用正方形表示）的样本组成的。 容易理解，某些格式错误的二进制与格式错误的八进制非常相似，这证明了拆分原始群集的合理性。 从统计角度来看，所解释的方差可能会产生不同的影响。 在某些情况下，只有几个组件足以确定类的特殊特征，但这通常是不正确的。 当属于不同类别的样本显示出相似性时，只能由于次级成分的差异而做出区分。 在处理包含几乎（甚至部分）重叠样本的数据集时，这一考虑非常重要。 进行降维时，数据科学家的主要任务不是检查总体解释的方差，而是了解是否存在受降维不利影响的区域。 在这种情况下，可以定义多个检测规则（例如，当样本x[i] ∈ R[1]或x[i] ∈ R[4] → x[i]具有y[k]标签）或尝试避免使用模型来创建此细分（在这种情况下，我们邀请您测试更复杂的 DBN 和更高维的输出表示形式）。

总结

在本章中，我们讨论了用于解决无监督任务的一些非常常见的神经模型。 自编码器使您可以查找数据集的低维表示形式，而没有对其复杂性的特定限制。 特别是，深度卷积网络的使用有助于检测和学习高级和低级几何特征，当内部代码也比原始维数短得多时，这可以导致非常准确的重构。 我们还讨论了如何为自编码器增加稀疏性，以及如何使用这些模型对样本进行降噪。 标准自编码器的一个稍有不同的变体是变分自编码器，它是一种生成模型，可以提高学习从中得出数据集的数据生成过程的能力。

Sanger 和 Rubner-Tavan 的网络是神经模型，能够在不进行任何统计预处理的情况下提取数据集的前k主成分。 它们还具有以在线方式自然工作的优势（尽管标准 PCA 经常需要整个数据集，即使存在表现稍逊于脱机算法的增量变体），也可以按降序提取组件。 我们讨论的最后一个模型是在无监督的情况下的 DBN。 我们描述了其构建基块 RBM 的生成属性，然后分析了此类模型如何学习数据生成过程的内部（通常为低维）表示。

在下一章中，我们将讨论其他神经模型：生成对抗网络（GAN）和自组织映射（SOM）。 前者可以学习输入分布并从中获取新样本，而后者则基于大脑某些特定区域的功能，并训练它们的单位以接受特定的输入模式。

问题

1. 在自编码器中，编码器和解码器都必须在结构上对称。 它是否正确？
2. 给定数据集X及其转换Y，根据自编码器产生的代码，可以在Y找到X中包含的所有信息。 它是否正确？
3. 代码z[i] ∈ (0, 1)^128的sum(z[i]) = 36。 稀疏吗？
4. 如果std(z[i]) = 0.03，代码是否稀疏？
5. Sanger 网络需要协方差矩阵的列作为输入向量。 它是否正确？
6. 我们如何确定 Rubner-Tavan 网络提取的每个成分的重要性？
7. 给定一个随机向量，h[i] ∈ R^m（m是 DBN 的输出维数），是否可以确定最可能对应的输入样本？

进一步阅读

• Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion, Vincent, P., Larochelle, H., Lajoie, I., Bengio, Y., and Manzagol, P., Journal of Machine Learning Research 11, 2010
• Sparse Autoencoder, CS294A, Ng, A., Stanford University
• Auto-Encoding Variational Bayes, Kingma. D. P. and Welling, M., arXiv:1312.6114 [stat.ML]
• Theoretical Neuroscience, Dayan, P. and Abbott, L. F., The MIT Press, 2005
• Optimal Unsupervised Learning in a Single-Layer Linear Feedforward Neural Network, Neural Networks, Sanger, T. D., 2, 1989
• A Self-Organizing Network for Principal-Components Analysis, Europhysics Letters, Rubner, J. and Tavan, P., 10(7), 1989
• Information Processing in Dynamical Systems: Foundations of Harmony Theory, Parallel Distributed Processing, Smolensky, Paul, Vol 1, The MIT Press, 1986
• A Practical Guide to Training Restricted Boltzmann Machines, Hinton, G., Dept. Computer Science, University of Toronto, 2010
• A Fast Learning Algorithm for Deep Belief Nets, Hinton G. E., Osindero S., and Teh Y. W., Neural Computation, 18/7, 2005
• Machine Learning Algorithms, Second Edition, Bonaccorso, G., Packt, 2018
• Mastering Machine Learning Algorithms, Bonaccorso, G., Packt, 2018

九、生成对抗网络和 SOM

在本章中，我们将结束无监督学习的整个过程，讨论一些可以用于执行数据生成过程的非常流行的神经模型，以及可以从中提取的新样本。 此外，我们将分析自组织映射的功能，该功能可以调整其结构，以便特定单元可以响应不同的输入模式。

特别是，我们将讨论以下主题：

• 生成对抗网络（GAN）
• 深度卷积 GAN（DCGAN）
• Wasserstein GAN（WGAN）
• 自组织映射（SOM）

技术要求

本章将介绍的代码需要以下内容：

• Python3.5+（强烈建议使用 Anaconda 发行版）
• 库如下：
  • SciPy 0.19+
  • NumPy 1.10+
  • Scikit-Learn 0.20+
  • Pandas 0.22+
  • Matplotlib 2.0+
  • Seaborn 0.9+
  • TensorFlow 1.5+
  • Keras 2+（仅适用于数据集工具函数）

可以在 GitHub 存储库中找到这些示例。

生成对抗网络

这些生成模型由 Goodfellow 和其他研究人员提出（在《生成对抗网络》中），以利用对抗训练的功能以及深度神经网络的灵活性。 无需过多的技术细节，我们就可以将对抗训练的概念作为一种基于博弈论的技术进行介绍，其目标是优化两个相互竞争的智能体。 当一个特工试图欺骗其对手时，另一名特工必须学习如何区分正确的输入和伪造的输入。 特别是，GAN 是一个模型，它分为两个定义明确的组件：

• 生成器
• 判别器（也称为评论家）

让我们首先假设有一个数据生成过程，p_data，以及一个数据集X，该数据集是从m样本中提取的：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WmCQmRw2-1681652675174)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/51747182-bf27-4942-aa5c-7bc1d719034b.png)]

为简单起见，假定数据集具有一个维度； 但是，这不是约束也不是限制。 生成器是一个参数化函数（通常使用神经网络），该函数馈入有噪声的样本，并提供n维向量作为输出：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zXrrZHrf-1681652675174)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/4579d40e-3f19-4f5b-8f1b-70ea0fe5e3be.png)]

换句话说，生成器是样本x ∈ R^n上均匀分布到另一分布p[g](x)的变换。 GAN 的主要目标如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bvX72J74-1681652675174)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/956dc503-ac1c-451e-89a1-2f47d07bb5d1.png)]

但是，与通过直接训练整个模型来实现这一目标的自编码器相反，在 GAN 中，目标是通过在生成器和判别器之间进行的游戏来实现的，这是另一个需要采样的参数化函数，x[i] ∈ R^n，并返回概率：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Kbmt7jfW-1681652675174)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/4bd5bc8f-ede6-45e8-80ea-543706b24852.png)]

判别器的作用是区分从p_data（返回大概率）提取的样本与由g(z; θ[g])（返回低概率）。 但是，由于生成器的目标是变得越来越有能力复制p_data，因此其作用是学习如何用数据生成过程的几乎完美复制品中的样本来欺骗判别器。 因此，考虑到判别器，目标是最大化以下条件：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5SM1APRW-1681652675174)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/6776cf30-d26d-4c1b-aa66-65165ebac3a2.png)]

但是，这是 minimax 游戏，这意味着两个对手A和B都必须尝试最小化（A） 和最大化（B），这是相同的目标。 在这种情况下，生成器的目标是最小化先前的双重成本函数的第二项：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OBfDL6RA-1681652675175)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/1c69083f-4200-4599-a7af-1b594ab3bc20.png)]

实际上，当两个智能体都成功地优化了目标时，判别器将能够区分从p_data提取的样本和异常值，并且生成器将能够输出属于p_data的合成样本。 但是，必须明确的是，可以通过使用单个目标来表达问题，并且训练过程的目标是找出最佳参数集，θ = {θ[d], θ[g]}，因此判别器将其最大化，而生成器将其最小化。 必须同时优化两个智能体，但是实际上，过程是交替的（例如，生成器，判别器，生成器等）。 目标可以用更紧凑的形式表示如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4aZ9dNhf-1681652675175)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/304d8dd9-8212-4b27-a550-71c85664a763.png)]

因此，通过解决以下问题可以达到最佳效果：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-w8fJXimI-1681652675175)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/3ef1bf38-3d09-434a-993d-0a410667c1fe.png)]

根据博弈论，这是一个不合作的博弈，它承认纳什均衡点。 当满足这种条件时，如果我们假设双方都知道对手的策略，那么他们就没有理由再改变自己的策略了。 在 GAN 的情况下，这种情况意味着一旦达到平衡（甚至只是理论上），生成器就可以继续输出样本，并确保它们不会被判别器误分类。 同时，判别器没有理由改变其策略，因为它可以完美地区分p_data和任何其他分布。 从动态角度来看，两个组件的训练速度都是不对称的。 尽管生成器通常需要更多的迭代，但判别器可以非常迅速地收敛。 但是，这样的过早收敛对于整体表现可能非常危险。 实际上，由于判别器提供的反馈，生成器也达到了最佳状态。 不幸的是，当梯度很小时，这种贡献可以忽略不计，其明显的结果是，生成器错过了提高其输出更好样本能力的机会（例如，当样本是图像时，它们的质量可能会保持非常低，甚至具有复杂的架构）。 这种情况并不取决于生成器固有的容量不足，而是取决于判别器收敛（或非常接近收敛）后开始应用的有限次校正。 在实践中，由于没有特定的规则，唯一有效的建议是在训练过程中检查两个损失函数。 如果判别器的损失下降得太快，而生成器的损失仍然很大，那么通常最好在单个判别器步骤中插入更多的生成器训练步骤。

分析 GAN

假设我们有一个 GAN，该 GAN 已通过使用从p_data(x)中提取的数据集X进行了适当的训练。 Goodfellow 等人证明，给定生成器分布p[g](x)，最佳判别器如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LeFZKmqb-1681652675175)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/bf275808-f597-4c3c-a017-6ecaa9f12a79.png)]

可以使用最佳判别器来重写全局目标：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7PJN0A2q-1681652675176)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/fb61b945-753c-4d3a-ae24-b25d49b47952.png)]

现在，我们可以扩展前面的表达式：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0hOIbBLi-1681652675176)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/ecbc89dd-1468-4030-9b3b-f8afd8001855.png)]

现在，让我们考虑两个分布a和b之间的 Kullback-Leibler 散度：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZLciP87o-1681652675176)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/9e4f728c-21ba-4c78-951a-099df4986119.png)]

考虑前面的表达式，经过一些简单的操作，很容易证明以下相等：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UTvIwdN1-1681652675176)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/ea76a19a-d431-4d64-8ab4-2353158ec476.png)]

因此，目标可以表示为数据生成过程和生成器分布之间的 Jensen-Shannon 散度的函数。 与 Kullback-Leibler 散度的主要区别在于0 ≤ D[JS](p_data || p[g]) ≤ log(2)，并且是对称的。 这种重新定义并不奇怪，因为 GAN 的真正目标是成为一个能够成功复制p_data的生成模型，如下图所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-42e4iaj7-1681652675176)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/d5d8548e-abc4-4567-9a42-2def53203f69.png)]

GAN 的目标是将生成的模型分布朝p_data方向移动，以尝试使重叠最大化

初始分布通常与目标分布完全不同； 因此，GAN 必须同时调整形状并将其移向p_data。 重叠完成后，Jensen-Shannon 散度达到最小值，并且优化完成。 但是，正如我们将在下一节中讨论的那样，由于 Jensen-Shannon 散度的特性，此过程并不总是如此平稳地运行，并且 GAN 可以达到次理想的极小值，离期望的最终配置很远。

模式崩溃

给定一个概率分布，最常出现的值（在离散情况下）或对应于概率密度函数最大值的值（在连续情况下）称为模式。 如果考虑后一种情况，则其 PDF 具有单个最大值的分布称为单峰。 当有两个局部极大值时，称为双峰，等（通常，当存在多个众数时，分布简称为多峰）。 以下屏幕快照显示了两个示例：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ldLHdLGn-1681652675177)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/a8df35ed-d5d1-4e6f-b381-f22b67ef545a.png)]

单峰（左）和双峰（右）分布的示例

当处理复杂的数据集时，我们无法轻松地估计模式数量。 但是，可以合理地假设数据生成过程是多模式的。 有时，当样本基于共同的结构时，可以有一个主导模式和几个次要模式。 但是通常，如果样本在结构上不同，则具有单一模式的可能性非常低（当然，如果对相同基本元素进行少量修改，则可能具有单一模式，但这不是要考虑的有效情况） 帐户）。

现在，让我们想象一下我们正在处理人脸图片的多模式分布（例如下一节将要讨论的示例中的人脸图片）。 模式的内容是什么？ 很难精确地回答这个问题，但是很容易理解，对应于最大数据生成过程的人脸应该包含数据集中最常见的元素（例如，如果 80% 的人留着胡须 ，我们可以合理地假设该模式将包含它）。

我们在使用 GAN 时面临的最著名，最棘手的问题之一就是模式崩溃，它涉及到次优的最终配置，其中生成器冻结在某个模式附近，并不断提供输出。 发生这种情况的原因非常难以分析（实际上，只有理论），但是我们可以理解如果重新考虑 minimax 游戏，为什么会发生这种情况。 当我们要训练两个不同的分量时，即使保证了纳什均衡，在几次迭代之后，对于最常见的模式，判别器也会变得非常有选择性。 当然，当训练生成器以欺骗判别器时，实现此目标的最简单方法是简单地避免所有采样远离模式。 这种行为增加了判别器的选择性，并创建了一个反馈过程，使 GAN 陷入只有数据生成过程只有一小部分区域的状态。

在梯度方面，判别器提供的用于优化生成器的信息很快变得非常稀缺，因为最常见的样本不需要任何调整。 另一方面，当生成器开始避免所有p(x)不接近最大值的样本时，它们不会将判别器暴露给新的，可能有效的样本，因此梯度将保持很小，直到消失为零。 不幸的是，没有可以用来避免此问题的全局策略，但是在本章中，我们将讨论一种建议的方法，以减轻模式崩溃（WGAN）的风险。 特别是，我们将把注意力集中在 Jensen-Shannon 发散的局限性上，在某些情况下，由于没有大的梯度，这可能导致 GAN 达到次优配置。 在本简介中，重要的是，不熟悉这些模型的读者应意识到风险，并能够在发生模式崩溃时识别出它。

此时，我们可以继续进行实际操作，并使用 TensorFlow 建模真实的 GAN。

深度卷积 GAN 的示例

现在，我们可以基于《使用深度卷积生成对抗网络的无监督表示学习》和 Olivetti faces 数据集，该数据集足够小以允许进行快速训练。

让我们首先加载数据集并标准化范围(-1, 1)中的值，如下所示：

from sklearn.datasets import fetch_olivetti_faces

faces = fetch_olivetti_faces(shuffle=True, random_state=1000)

X_train = faces['images']
X_train = (2.0 * X_train) - 1.0

width = X_train.shape[1]
height = X_train.shape[2]

以下屏幕快照显示了一些示例面孔：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-G60JFzTZ-1681652675177)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/49bdaa5a-37a8-4fce-b39c-fa8b9ec22294.png)]

从 Olivetti 人脸数据集中抽取的人脸样本

即使所有人脸的结构都相似，但眼睛（戴或不戴眼镜），鼻子和嘴巴的形状也存在细微差别。 而且，有些人留着胡须，表情却大不相同（微笑，严肃，盯着相机远处的东西，等等）。 因此，我们需要期待多峰分布，可能具有对应于平均人脸结构的主要模式，以及对应于具有特定，共同特征的子集的其他几种模式。

此时，我们可以定义主要常量，如下所示：

nb_samples = 400
code_length = 512
nb_epochs = 500
batch_size = 50
nb_iterations = int(nb_samples / batch_size)

有400 64×64 灰度样本（每个样本对应 4,096 个分量）。 在此示例中，我们选择采用具有512分量的噪声代码向量，并以50个样本批量训练500周期的模型。 这样的值不是基于黄金规则的，因为（尤其是对于 GAN）几乎不可能知道哪个设置会产生最佳结果。 因此，与往常一样，我强烈建议在做出决定之前检查不同的超参数集。

当训练过程不太长时，可以使用一组统一采样的超参数（例如批大小属于{20, 50, 100, 200}）检查生成器和判别器的平均损失。 例如，如果某个最佳值似乎在范围(50, 100)内，那么一个好的策略是提取一些随机值并重新训练模型。 可以重复进行此过程，直到采样值之间的差异可以忽略不计为止。 当然，考虑到这些模型的复杂性，只有使用专用硬件（即多个 GPU 或 TPU）才能进行彻底的搜索。 因此，另一个建议是从经过测试的配置开始（即使上下文不同），并进行小的修改，以便针对特定任务优化它们。 在此示例中，我们根据原始论文设置了许多值，但是我邀请读者在自定义更改后重新运行代码并观察差异。

现在，我们可以基于以下结构为生成器定义 DAG：

• 具有 1,024 个4×4过滤器的 2D 卷积，步幅为(1, 1)，有效填充和线性输出
• 批量规范化和 LReLU 激活（当输入值为负时，表现更高；实际上，当x < 0时，标准 ReLU 的梯度为零，而 LReLU 的常数较小） 允许稍微修改的梯度）
• 带有(2, 2)步幅，相同填充和线性输出的 512 个4×4过滤器的 2D 卷积
• 批量规范化和 LReLU 激活
• 256 个4×4过滤器的 2D 卷积，步幅为(2, 2)，相同填充，以及线性输出
• 批量规范化和 LReLU 激活
• 具有 128 个4×4过滤器的 2D 卷积，步幅为(2, 2)，相同填充，以及线性输出
• 批量规范化和 LReLU 激活
• 具有 1 个4×4过滤器的 2D 卷积，步幅为(2, 2)，相同填充，以及双曲正切输出

以下代码段显示了生成器的代码：

import tensorflow as tf

def generator(z, is_training=True):
    with tf.variable_scope('generator'):
        conv_0 = tf.layers.conv2d_transpose(inputs=z,
                                            filters=1024,
                                            kernel_size=(4, 4),
                                            padding='valid')

        b_conv_0 = tf.layers.batch_normalization(inputs=conv_0, training=is_training)

        conv_1 = tf.layers.conv2d_transpose(inputs=tf.nn.leaky_relu(b_conv_0),
                                            filters=512,
                                            kernel_size=(4, 4),
                                            strides=(2, 2),
                                            padding='same')

        b_conv_1 = tf.layers.batch_normalization(inputs=conv_1, training=is_training)

        conv_2 = tf.layers.conv2d_transpose(inputs=tf.nn.leaky_relu(b_conv_1),
                                            filters=256,
                                            kernel_size=(4, 4),
                                            strides=(2, 2),
                                            padding='same')

        b_conv_2 = tf.layers.batch_normalization(inputs=conv_2, training=is_training)

        conv_3 = tf.layers.conv2d_transpose(inputs=tf.nn.leaky_relu(b_conv_2),
                                            filters=128,
                                            kernel_size=(4, 4),
                                            strides=(2, 2),
                                            padding='same')

        b_conv_3 = tf.layers.batch_normalization(inputs=conv_3, training=is_training)

        conv_4 = tf.layers.conv2d_transpose(inputs=tf.nn.leaky_relu(b_conv_3),
                                            filters=1,
                                            kernel_size=(4, 4),
                                            strides=(2, 2),
                                            padding='same')

        return tf.nn.tanh(conv_4)

该代码很简单，但是有助于阐明对变量范围上下文的需要（通过命令tf.variable_scope('generator')定义）。 由于我们需要以其他方式训练模型，因此在优化生成器时，仅必须更新其变量。 因此，我们在命名范围内定义了所有层，从而允许强制优化器仅工作所有可训练变量的子集。

判别器的 DAG 基于以下对称结构：

• 具有(2, 2)步幅的 1284×4个过滤器的 2D 卷积，相同填充，以及 LReLU 输出
• 256 个4×4过滤器的 2D 卷积，步幅为(2, 2)，相同填充，以及线性输出
• 批量规范化和 LReLU 激活
• 带有 512 个4×4过滤器的 2D 卷积，步幅为(2, 2)，相同填充，以及线性输出
• 批量规范化和 LReLU 激活
• 具有 1,0244×4过滤器的 2D 卷积，步幅为(2, 2)，相同填充，以及线性输出
• 批量规范化和 LReLU 激活
• 具有 1 个4×4过滤器的 2D 卷积，步幅为(2, 2)，有效填充，以及线性输出（预期输出为 sigmoid，可以表示一个概率，但是我们将直接在损失函数内部执行此变换）

判别器的代码为，如下所示：

import tensorflow as tf

def discriminator(x, is_training=True, reuse_variables=True):
    with tf.variable_scope('discriminator', reuse=reuse_variables):
        conv_0 = tf.layers.conv2d(inputs=x,
                                  filters=128,
                                  kernel_size=(4, 4),
                                  strides=(2, 2),
                                  padding='same')

        conv_1 = tf.layers.conv2d(inputs=tf.nn.leaky_relu(conv_0),
                                  filters=256,
                                  kernel_size=(4, 4),
                                  strides=(2, 2),
                                  padding='same')

        b_conv_1 = tf.layers.batch_normalization(inputs=conv_1, training=is_training)

        conv_2 = tf.layers.conv2d(inputs=tf.nn.leaky_relu(b_conv_1),
                                  filters=512,
                                  kernel_size=(4, 4),
                                  strides=(2, 2),
                                  padding='same')

        b_conv_2 = tf.layers.batch_normalization(inputs=conv_2, training=is_training)

        conv_3 = tf.layers.conv2d(inputs=tf.nn.leaky_relu(b_conv_2),
                                  filters=1024,
                                  kernel_size=(4, 4),
                                  strides=(2, 2),
                                  padding='same')

        b_conv_3 = tf.layers.batch_normalization(inputs=conv_3, training=is_training)

        conv_4 = tf.layers.conv2d(inputs=tf.nn.leaky_relu(b_conv_3),
                                  filters=1,
                                  kernel_size=(4, 4),
                                  padding='valid')

        return conv_4

同样，在这种情况下，我们需要声明一个专用的变量作用域。 但是，由于判别器在两个不同的上下文中使用（即，对真实样本和生成样本的评估），我们需要在第二个声明中要求重用变量。 如果未设置此类标志，则对函数的每次调用都会产生新的变量集，对应于不同的标识符。

声明了两个主要组件后，我们可以初始化图并为 GAN 设置整个 DAG，如下所示：

import tensorflow as tf

graph = tf.Graph()

with graph.as_default():
    input_x = tf.placeholder(tf.float32, shape=(None, width, height, 1))
    input_z = tf.placeholder(tf.float32, shape=(None, code_length))
    is_training = tf.placeholder(tf.bool)

    gen = generator(z=tf.reshape(input_z, (-1, 1, 1, code_length)), is_training=is_training)

    discr_1_l = discriminator(x=input_x, is_training=is_training, reuse_variables=False)
    discr_2_l = discriminator(x=gen, is_training=is_training, reuse_variables=True)

    loss_d_1 = tf.reduce_mean(
            tf.nn.sigmoid_cross_entropy_with_logits(labels=tf.ones_like(discr_1_l), logits=discr_1_l))
    loss_d_2 = tf.reduce_mean(
            tf.nn.sigmoid_cross_entropy_with_logits(labels=tf.zeros_like(discr_2_l), logits=discr_2_l))
    loss_d = loss_d_1 + loss_d_2

    loss_g = tf.reduce_mean(
            tf.nn.sigmoid_cross_entropy_with_logits(labels=tf.ones_like(discr_2_l), logits=discr_2_l))

    variables_g = [variable for variable in tf.trainable_variables() if variable.name.startswith('generator')]
    variables_d = [variable for variable in tf.trainable_variables() if variable.name.startswith('discriminator')]

    with tf.control_dependencies(tf.get_collection(tf.GraphKeys.UPDATE_OPS)):
        training_step_d = tf.train.AdamOptimizer(0.0001, beta1=0.5).minimize(loss=loss_d, var_list=variables_d)
        training_step_g = tf.train.AdamOptimizer(0.0005, beta1=0.5).minimize(loss=loss_g, var_list=variables_g)

第一块包含占位符的声明。 为了清楚起见，虽然input_x和input_z的目的很容易理解，但is_training可能不太明显。 此布尔值标志的目的是允许在生产阶段禁用批量规范化（必须仅在训练阶段有效）。 下一步包括声明生成器和两个判别器（它们在形式上是相同的，因为变量是共享的，但是其中一个被提供了真实的样本，而另一个必须评估生成器的输出）。 然后，是时候定义损失函数了，它是基于一种可以加快计算速度并增加数值稳定性的技巧。

函数tf.nn.sigmoid_cross_entropy_with_logits()接受对率（这就是为什么我们没有将 Sigmoid 变换直接应用于判别器输出的原因），并允许我们执行以下向量计算：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dSbSUD5Z-1681652675177)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/cb4a2f99-5422-4c6f-bc83-588e81037426.png)]

因此，由于loss_d_1是真实样本的损失函数，因此我们使用运算符tf.ones_like()将所有标签设置为 1； 因此，S 形交叉熵的第二项变为零，结果如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WhiI829t-1681652675177)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/cc9c07fc-72da-4fae-b60c-9c17149f81cc.png)]

相反，loss_d_2恰好需要 Sigmoid 交叉熵的第二项。 因此，我们将所有标签设置为零，以获得损失函数：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vFPVPHyN-1681652675177)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/4bebedd1-9438-42e7-aae9-c18aa72d2a49.png)]

相同的概念适用于生成器损失函数。 下一步需要定义两个 Adam 优化器。 如前所述，我们需要隔离变量以进行隔行训练。 因此，minimize()函数现在被提供了损失和必须更新的变量集。 TensorFlow 官方文档中建议使用上下文声明tf.control_dependencies(tf.get_collection(tf.GraphKeys.UPDATE_OPS))，只要采用批量规范化，其目标是仅在计算均值和方差之后才允许执行训练步骤（有关此技术的更多详细信息，请检查原始论文：《批量规范化：通过减少内部协变量移位》。

此时，我们可以创建一个会话并初始化所有变量，如下所示：

import tensorflow as tf

session = tf.InteractiveSession(graph=graph)
tf.global_variables_initializer().run()

一旦一切准备就绪，就可以开始训练过程。 以下代码片段显示了对判别器和生成器进行交替训练的代码：

import numpy as np

samples_range = np.arange(nb_samples)

for e in range(nb_epochs):
    d_losses = []
    g_losses = []

    for i in range(nb_iterations):
        Xi = np.random.choice(samples_range, size=batch_size)
        X = np.expand_dims(X_train[Xi], axis=3)
        Z = np.random.uniform(-1.0, 1.0, size=(batch_size, code_length)).astype(np.float32)

        _, d_loss = session.run([training_step_d, loss_d],
                                    feed_dict={
                                        input_x: X,
                                        input_z: Z,
                                        is_training: True
                                    })
        d_losses.append(d_loss)

        Z = np.random.uniform(-1.0, 1.0, size=(batch_size, code_length)).astype(np.float32)

        _, g_loss = session.run([training_step_g, loss_g],
                                    feed_dict={
                                        input_x: X,
                                        input_z: Z,
                                        is_training: True
                                        })

        g_losses.append(g_loss)

    print('Epoch {}) Avg. discriminator loss: {} - Avg. generator loss: {}'.format(e + 1, np.mean(d_losses), np.mean(g_losses)))

在这两个步骤中，我们为网络提供一批真实的图像（在生成器优化期间不会使用）和统一采样的代码Z，其中每个分量为z[i] ~ U(-1, 1)。 为了减轻模式崩溃的风险，我们将在每次迭代开始时对集合进行洗牌。 这不是一个可靠的方法，但是至少可以确保避免可能导致 GAN 达到次优配置的相互关系。

在训练过程结束时，我们可以生成一些样本面孔，如下所示：

import numpy as np

Z = np.random.uniform(-1.0, 1.0, size=(20, code_length)).astype(np.float32)

Ys = session.run([gen],
                 feed_dict={
                     input_z: Z,
                     is_training: False
                 })

Ys = np.squeeze((Ys[0] + 1.0) * 0.5 * 255.0).astype(np.uint8)

结果显示在以下屏幕截图中：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zwOvflNg-1681652675178)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/29d10031-02b1-448c-b339-0163f2d2bf5e.png)]

DCGAN 生成的样本人脸

可以看到，质量非常高，较长的训练阶段会有所帮助（以及更深的超参数搜索）。 但是，GAN 已成功学习了如何通过使用同一组属性来生成新面孔。 表达式和视觉元素（例如，眼睛的形状，眼镜的存在等）都重新应用于不同的模型，以便产生从相同原始数据生成过程中绘制的潜在面孔。 例如，第七名和第八名基于具有修改属性的一个人。 原始图片如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GAEdBdTP-1681652675178)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/eeea0b30-618e-4267-9766-78baabc05fac.png)]

对应于 Olivetti 人之一的原始图片

嘴的结构对于两个生成的样本都是相同的，但是从第二个样本来看，我们可以确认已经从其他样本中提取了许多元素（鼻子，眼睛，前额和方向），从而产生了不存在的人。 即使模型正常工作，也会出现部分模式崩溃，因为某些面孔（具有其相对属性，例如眼镜）比其他面孔更常见。 相反，一些女性面孔（数据集中的少数）已与男性属性合并，从而产生了样本，例如包含所生成样本的图像的第一行的第二个或底部行的第八个。 作为练习，我邀请读者使用不同的参数和其他数据集（包含灰度和 RGB 图像，例如 Cifar-10 或 STL-10）来重新训练模型。

The screenshots that are shown in this and other examples in this chapter are often based on random generations; therefore, in order to increase the reproducibility, I suggest setting both the NumPy and TensorFlow random seed equal to 1000. The commands are: np.random.seed(1000) and tf.set_random_seed(1000).

Wasserstein GAN

给定概率分布p(x)，集合D[p] = {x: p(x) > 0}被称为支撑 。 如果p(x)和q(x)的两个分布具有脱节的支撑（即D[p] ∩ D[q] = {∅}），詹森-香农散度等于log(2)。 这意味着梯度为零，并且无法进行任何校正。 在涉及 GAN 的一般情况下， p[g](x)和p_data完全不可能重叠（ 但是，您可以期望有最小的重叠）； 因此，梯度很小，权重的更新也很小。 这样的问题可能会阻止训练过程，并使 GAN 陷入无法逃避的次优配置状态。 因此， Arjovsky，Chintala 和 Bottou （在《Wasserstein GAN》中）基于称为 Wasserstein 距离的更稳健的差异度量，提出了一个略有不同的模型。（或“地球移动者”的距离）：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cRpyLPkk-1681652675178)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/cf700f07-35ed-4e38-80db-a046bbe07d21.png)]

为了理解前面的公式，必须说∏(p_data, p[g])是包含所有可能的联合分布的集合。 数据生成过程和生成器分布。 因此，Wasserstein 距离等于范数||x - y||的期望值的最小值。假设一对(x, y)是分布μ ~ ∏(p_data, p[g])。 即使这个概念很简单，这种定义也不是很直观，并且可以通过考虑两个二维 Blob（其距离是两个最近点之间的距离）来概括。 显然，支撑支点不相交的问题已被完全克服，此外，度量也与实际分布距离成比例。 不幸的是，我们没有使用有限集。 因此，Wasserstein 距离的计算可能非常低效，并且几乎不可能用于现实生活中的任务。 但是， Kantorovich-Rubinstein 定理（由于超出了本书的范围，因此未进行全面分析）使我们可以通过使用特殊的支持函数f(x)来简化表达式：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Lx4BbZ5a-1681652675178)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/6409c4e2-844b-44d2-bd22-655dd88d2e4b.png)]

该定理施加的主要约束是f(x)必须是 L-Lipschitz 函数，也就是说，给定非负常数L，则适用 ：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eBbYXLSq-1681652675178)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/a97ddbd4-a379-4fc0-aad7-4de7a552abcd.png)]

考虑使用神经网络参数化的函数f(·)，全局目标变为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4pXrcxE8-1681652675179)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/ac4ed2f2-c377-4788-9950-1e7768520a25.png)]

在这种特定情况下，判别器通常被称为批判者，因此f(x; θ[c])扮演着这个角色。 由于这样的函数必须是 L-Lipschitz，因此作者建议在应用校正后就剪切所有变量$1[$2]：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-a2wrufT9-1681652675179)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/c6e68853-8d2d-4ea5-9670-8fe1ad4803ac.png)]

该方法不是非常有效，因为它会减慢学习过程。 但是，当函数执行一组有限变量的操作时，假定输出始终受常数约束，并且可以应用 Kantorovich-Rubinstein 定理。 当然，由于参数化通常需要许多变量（有时数百万或更多），因此裁剪常数应保持很小（例如 0.01）。 此外，由于剪辑的存在会影响批判者的训练速度，因此也有必要在每次迭代中增加批判者训练步骤的数量（例如，批判者 5 次，生成器 1 次，依此类推。 ）。

将 DCGAN 转变为 WGAN

在此示例中，我们将使用 Fashion MNIST 数据集（由 Keras 直接提供）基于 Wasserstein 距离实现 DCGAN。 该集合由 60,000 张 28×28 灰度的衣服图像组成，由 Zalando 引入，以替代标准 MNIST 数据集，该数据集的类别太容易被许多分类器分离。 考虑到此类网络所需的训练时间，我们决定将过程限制为 5,000 个样本，但是拥有足够资源的读者可以选择增加或消除此限制。

第一步包括加载，切片和规范化数据集（在(-1, 1)范围内），如下所示：

import numpy as np

from keras.datasets import fashion_mnist

nb_samples = 5000

(X_train, _), (_, _) = fashion_mnist.load_data()
X_train = X_train.astype(np.float32)[0:nb_samples] / 255.0
X_train = (2.0 * X_train) - 1.0

width = X_train.shape[1]
height = X_train.shape[2]

以下屏幕快照显示了一些示例：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Otxl1BaA-1681652675179)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/aac13c86-1214-4c02-9078-f6b3fd5ecbf3.png)]

从 Fashion MNIST 数据集中提取的样本

现在，我们可以基于 DCGAN 的同一层定义生成器 DAG，如下所示：

• 具有 1,024 个4×4过滤器的 2D 卷积，步幅为(1, 1)，有效填充，以及线性输出
• 批量规范化和 LReLU 激活
• 带有 512 个4×4过滤器的 2D 卷积，步幅为(2, 2)，相同填充，以及线性输出
• 批量规范化和 LReLU 激活
• 256 个4×4过滤器的 2D 卷积，步幅为(2, 2)，相同填充，以及线性输出
• 批量规范化和 LReLU 激活
• 具有 128 个4×4过滤器的 2D 卷积，步幅为(2, 2)，相同填充，以及线性输出
• 批量规范化和 LReLU 激活
• 具有 1 个4×4过滤器的 2D 卷积，步幅为(2, 2)，相同填充，以及双曲正切输出

该代码显示在以下代码片段中：

import tensorflow as tf

def generator(z, is_training=True):
    with tf.variable_scope('generator'):
        conv_0 = tf.layers.conv2d_transpose(inputs=z,
                                            filters=1024,
                                            kernel_size=(4, 4),
                                            padding='valid')

        b_conv_0 = tf.layers.batch_normalization(inputs=conv_0, training=is_training)

        conv_1 = tf.layers.conv2d_transpose(inputs=tf.nn.leaky_relu(b_conv_0),
                                            filters=512,
                                            kernel_size=(4, 4),
                                            strides=(2, 2),
                                            padding='same')

        b_conv_1 = tf.layers.batch_normalization(inputs=conv_1, training=is_training)

        conv_2 = tf.layers.conv2d_transpose(inputs=tf.nn.leaky_relu(b_conv_1),
                                            filters=256,
                                            kernel_size=(4, 4),
                                            strides=(2, 2),
                                            padding='same')

        b_conv_2 = tf.layers.batch_normalization(inputs=conv_2, training=is_training)

        conv_3 = tf.layers.conv2d_transpose(inputs=tf.nn.leaky_relu(b_conv_2),
                                            filters=128,
                                            kernel_size=(4, 4),
                                            strides=(2, 2),
                                            padding='same')

        b_conv_3 = tf.layers.batch_normalization(inputs=conv_3, training=is_training)

        conv_4 = tf.layers.conv2d_transpose(inputs=tf.nn.leaky_relu(b_conv_3),
                                            filters=1,
                                            kernel_size=(4, 4),
                                            strides=(2, 2),
                                            padding='same')

        return tf.nn.tanh(conv_4)

评论者的 DAG 基于以下几组：

• 具有(2, 2)步幅的 1284×4个过滤器的 2D 卷积，相同填充，以及 LReLU 输出
• 256 个4×4过滤器的 2D 卷积，步幅为(2, 2)，相同填充，以及线性输出
• 批量规范化和 LReLU 激活
• 带有 512 个4×4过滤器的 2D 卷积，步幅为(2, 2)，相同填充，以及线性输出
• 批量规范化和 LReLU 激活
• 具有 1,0244×4过滤器的 2D 卷积，步幅为(2, 2)，相同填充，以及线性输出
• 批量规范化和 LReLU 激活
• 具有 1 个4×4过滤器的 2D 卷积，步幅为(2, 2)，有效填充和线性输出

相应的代码块为，如下所示：

import tensorflow as tf

def critic(x, is_training=True, reuse_variables=True):
    with tf.variable_scope('critic', reuse=reuse_variables):
        conv_0 = tf.layers.conv2d(inputs=x,
                                  filters=128,
                                  kernel_size=(4, 4),
                                  strides=(2, 2),
                                  padding='same')

        conv_1 = tf.layers.conv2d(inputs=tf.nn.leaky_relu(conv_0),
                                  filters=256,
                                  kernel_size=(4, 4),
                                  strides=(2, 2),
                                  padding='same')

        b_conv_1 = tf.layers.batch_normalization(inputs=conv_1, training=is_training)

        conv_2 = tf.layers.conv2d(inputs=tf.nn.leaky_relu(b_conv_1),
                                  filters=512,
                                  kernel_size=(4, 4),
                                  strides=(2, 2),
                                  padding='same')

        b_conv_2 = tf.layers.batch_normalization(inputs=conv_2, training=is_training)

        conv_3 = tf.layers.conv2d(inputs=tf.nn.leaky_relu(b_conv_2),
                                  filters=1024,
                                  kernel_size=(4, 4),
                                  strides=(2, 2),
                                  padding='same')

        b_conv_3 = tf.layers.batch_normalization(inputs=conv_3, training=is_training)

        conv_4 = tf.layers.conv2d(inputs=tf.nn.leaky_relu(b_conv_3),
                                  filters=1,
                                  kernel_size=(4, 4),
                                  padding='valid')

        return conv_4

由于与 DCGAN 没有特别的区别，因此无需添加其他注释。 因此，我们可以继续进行图的定义和整体 DAG ，如下所示：

import tensorflow as tf

nb_epochs = 100
nb_critic = 5
batch_size = 64
nb_iterations = int(nb_samples / batch_size)
code_length = 100

graph = tf.Graph()

with graph.as_default():
    input_x = tf.placeholder(tf.float32, shape=(None, width, height, 1))
    input_z = tf.placeholder(tf.float32, shape=(None, code_length))
    is_training = tf.placeholder(tf.bool)

    gen = generator(z=tf.reshape(input_z, (-1, 1, 1, code_length)), is_training=is_training)

    r_input_x = tf.image.resize_images(images=input_x, size=(64,64),    
                                       method=tf.image.ResizeMethod.BICUBIC)

     crit_1_l = critic(x=r_input_x, is_training=is_training, reuse_variables=False)
     crit_2_l = critic(x=gen, is_training=is_training, reuse_variables=True)

     loss_c = tf.reduce_mean(crit_2_l - crit_1_l)
     loss_g = tf.reduce_mean(-crit_2_l)

     variables_g = [variable for variable in tf.trainable_variables() 
                     if variable.name.startswith('generator')]
     variables_c = [variable for variable in tf.trainable_variables() 
                     if variable.name.startswith('critic')]

     with tf.control_dependencies(tf.get_collection(tf.GraphKeys.UPDATE_OPS)):
         optimizer_c = tf.train.AdamOptimizer(0.00005, beta1=0.5, beta2=0.9).\
                             minimize(loss=loss_c, var_list=variables_c)

         with tf.control_dependencies([optimizer_c]):
             training_step_c = tf.tuple(tensors=[
                                     tf.assign(variable, tf.clip_by_value(variable, -0.01, 0.01))
                                                             for variable in variables_c])

         training_step_g = tf.train.AdamOptimizer(0.00005, beta1=0.5, beta2=0.9).\
                                  minimize(loss=loss_g, var_list=variables_g)

通常，第一步是声明占位符，该占位符与 DCGAN 相同。 但是，由于已经针对 64×64 图像优化了模型（特别是卷积或转置卷积的序列），因此我们将使用tf.image.resize_images()方法来调整原始样本的大小。 此操作将导致有限的质量损失； 因此，在生产应用中，我强烈建议您使用针对原始输入大小优化的模型。 在生成器和标注器都声明之后（如我们在上一个示例中讨论的那样，由于需要分别优化损失函数，因此我们需要两个实例共享相同的变量），我们可以设置损失。 在这种情况下，它们的计算非常简单且快速，但是我们为此付出了代价，并为此网络可以应用更小的校正。 实际上，在这种情况下，我们并没有直接最小化批评者损失函数； 相反，我们首先使用运算符optimizer_c计算并应用梯度，然后使用运算符training_step_c裁剪所有评论者变量。 因为我们只想调用此运算符，所以已在使用指令tf.control_dependencies([optimizer_c])定义的上下文中声明了它。 这样，当请求一个会话来计算traning_step_c时，TensorFlow 将注意首先运行optimizer_c，但是只有在结果准备好后，才会执行 main 命令（简单地裁剪变量）。 正如我们在理论中所解释的那样，此步骤对于保证评论者仍然具有 L-Lipschitz 函数是必要的，因此，允许使用从 Kantorovich-Rubinstein 定理得到的简化 Wasserstein 距离表达式。

当图完全定义后，可以创建一个会话并初始化所有变量，如下所示：

import tensorflow as tf

session = tf.InteractiveSession(graph=graph)
tf.global_variables_initializer().run()

现在，所有组件都已设置好，我们准备开始训练过程，该过程分为标注者训练步骤的nb_critic（在我们的情况下为五次）迭代和生成器训练步骤的一次执行，如下：

import numpy as np

samples_range = np.arange(X_train.shape[0])

for e in range(nb_epochs):
    c_losses = []
    g_losses = []

    for i in range(nb_iterations):
        for j in range(nb_critic):
            Xi = np.random.choice(samples_range, size=batch_size)
            X = np.expand_dims(X_train[Xi], axis=3)
            Z = np.random.uniform(-1.0, 1.0, size=(batch_size, code_length)).astype(np.float32)

            _, c_loss = session.run([training_step_c, loss_c],
                                        feed_dict={
                                            input_x: X,
                                            input_z: Z,
                                            is_training: True
                                        })
            c_losses.append(c_loss)

        Z = np.random.uniform(-1.0, 1.0, size=(batch_size, code_length)).astype(np.float32)

        _, g_loss = session.run([training_step_g, loss_g],
                                    feed_dict={
                                        input_x: np.zeros(shape=(batch_size, width, height, 1)),
                                        input_z: Z,
                                        is_training: True
                                    })

        g_losses.append(g_loss)

    print('Epoch {}) Avg. critic loss: {} - Avg. generator loss: {}'.format(e + 1,
                                                                            np.mean(c_losses),
                                                                            np.mean(g_losses)))

在此过程结束时（可能会很长，尤其是在没有任何 GPU 支持的情况下可能会很长），为了获得视觉确认，我们可以再次生成一些示例，如下所示：

import numpy as np

Z = np.random.uniform(-1.0, 1.0, size=(30, code_length)).astype(np.float32)

Ys = session.run([gen],
                  feed_dict={
                      input_z: Z,
                      is_training: False
                  })

Ys = np.squeeze((Ys[0] + 1.0) * 0.5 * 255.0).astype(np.uint8)

结果显示在以下屏幕截图中：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-C6qX4YYm-1681652675179)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/c547737d-8732-4c0e-bcb3-2b1ab893d875.png)]

WGAN 生成的样本

可以看到，WGAN 已收敛到合理的最终配置。 图像质量受大小调整操作的强烈影响； 但是，有趣的是，生成的样本平均比原始样本要复杂。 例如，衣服的质地和形状受其他因素（例如，包和鞋子）的影响，结果是模型不规则，新颖样本数量增加。 但是，与 Olivetti 人脸数据集相反，在这种情况下，很难理解样本是否由异质属性的混合物组成，因为数据生成过程（例如标准 MNIST）具有至少 10 种原始的类。

WGAN 不会陷入模式崩溃，但是不同区域的强烈分离使模型无法轻松合并元素，正如我们在人脸观察到的那样。 作为练习，我邀请读者对 Olivetti 人脸数据集重复该示例，找到最佳的超参数配置，并将结果与​​标准 DCGAN 获得的结果进行比较。

自组织映射

自组织映射是 Willshaw 和 Von Der Malsburg 首次提出的模型（在《如何通过自组织建立模式化的神经连接》中），目的是找到一种描述大脑中发生的不同现象的方法。 实际上，他们观察到许多动物的大脑的某些区域可以发展出内部组织的结构，这些结构的子组件相对于特定的输入模式（例如，某些视觉皮层区域对垂直或水平带非常敏感）可以选择性地接受。 SOM 的中心思想可以通过考虑聚类过程来综合，该聚类过程旨在找出样本的低级属性，这要归功于其对聚类的分配。 主要的实际差异是，在 SOM 中，单个单元通过称为赢家通吃的学习过程，成为一部分样本总体（即数据生成过程的区域）的代表。 。 这样的训练过程首先是引起所有单元（我们将其称为神经元）的响应并增强所有权重，然后通过减小最活跃单元周围的影响区域来进行，直到单个单元成为唯一的响应神经元为止。 给定输入模式。

下图综合了该过程：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IfJaRWIO-1681652675180)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/0603623a-f55d-4792-a188-2b84df0f58c7.png)]

SOM 开发的墨西哥帽选择性

在初始步骤中，许多单元会响应相同的输入模式，但是我们已经可以观察到x[i]附近的优势。 但是，立即选择此设备可能会导致收敛过早，从而导致准确率下降。 这就是为什么获胜单元周围的半径逐渐减小的原因（观察到一种称为墨西哥帽的现象，因为其形状特殊）。 当然，在此过程中，最初的获胜单元无法保持稳定； 因此，重要的是要避免半径的快速减小，以免引起其他潜在单位被引出。 当呈现特定模式时，当神经元保持最活跃时，它将被略微转换为实际的赢家，因此，这将花费全部，因为不会再加强任何其他单元。

一些非常著名和有用的 SOM 是 Kohonen 映射（首次出现在《拓扑正确特征映射的自组织形成》）。 它们的结构像投影到由N神经元组成的二维流形（最经典的情况是平坦的二维区域）上的平面一样。 从现在开始，为简单起见，我们将考虑映射到包含k×p单元的矩阵的曲面，每个曲面均使用突触权重w[ij] ∈ R^n进行建模 （大小与输入模式相同，x[i] ∈ R^n）。 因此，权重矩阵变为W(i, j) ∈ R^(k×p×n)。 从实际的角度来看，在此模型中，由于不执行内部转换，因此神经元通过相应的权重向量表示。 当呈现模式x[i]时，获胜神经元n[w]（作为元组）的确定如下： 使用以下规则：*

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eqtdh1Sg-1681652675180)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/1d22e1e2-5d4d-472e-90eb-af603c0116eb.png)]

训练过程通常分为两个不同的阶段：调整和收敛。 在调整阶段，更新会扩展到获胜单元的所有邻居，而在后者期间，只会增强权重W(n[w])。 但是，平滑而渐进的下降比快速下降更可取； 因此， n[s](i, j)的邻域大小的常见选择是基于径向基函数（RBF）具有指数衰减的方差：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gFMSUMe8-1681652675180)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/1cc30811-63e7-4ceb-a338-df23c28ca834.png)]

初始方差（与最大邻域成比例）为x[i]，并且根据时间常数τ呈指数衰减。 根据经验，当t > 4τ时，σ(t) ≈ 0，因此τ应该设置为 1/4 调整阶段的训练周期数：τ = 0.25•t[adj]。 一旦定义了邻域，就可以根据它们与每个样本的不相似性来更新所有成员的权重，x[i]：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-v6oXe2Bb-1681652675180)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/13a00879-7f4e-4444-a3e9-7cb93b92e001.png)]

在先前的公式中，学习率η(t)也是训练周期的函数，因为最好在早期（尤其是在调整阶段）施加更大的灵活性 ，但最好在收敛阶段设置较小的η，以便进行较小的修改。 降低学习率的一个非常常见的选择类似于邻域大小：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7S8rQud2-1681652675180)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/d9a02b2e-3f25-46de-abc6-0030f3866ecc.png)]

学习规则的作用是迫使获胜单元的权重接近特定模式，因此在训练过程结束时，每个模式都应引起代表一个定义明确的特征集的单个单元的响应。 。 形容词的自组织性源自这种模型必须优化单元的能力，以便使相似的模式彼此靠近（例如，如果竖线引起单元的响应，则稍微旋转的单元应引起单元的响应）。 邻居）。

Kohonen 映射的示例

在此示例中，我们要训练一个 8×8 正方形 Kohonen 映射以接受 Olivetti 人脸数据集。 由于每个样本都是 64×64 灰度图像，因此我们需要分配一个形状等于（8，8，4,096）的权重矩阵。 训练过程可能会很长； 因此，我们会将映射限制为 100 个随机样本（当然，读者可以自由删除此限制，并使用整个数据集训练模型）。

像往常一样，让我们​​开始加载并规范化数据集，如下所示：

import numpy as np

from sklearn.datasets import fetch_olivetti_faces

faces = fetch_olivetti_faces(shuffle=True)
Xcomplete = faces['data'].astype(np.float64) / np.max(faces['data'])
np.random.shuffle(Xcomplete)
X = Xcomplete[0:100]

现在，让我们为距离函数的方差σ(t)以及学习率η(t)定义指数衰减函数，如下所示[ ：

import numpy as np

eta0 = 1.0 sigma0 = 3.0 tau = 100.0 def eta(t):
 return eta0 * np.exp(-float(t) / tau)

def sigma(t):
 return float(sigma0) * np.exp(-float(t) / tau)

在该示例中，我们采用初始学习率η(0) = 1，半径方差σ(0) = 3* 。 之所以选择时间常数等于 100，是因为我们计划执行 500 个调整迭代和500收敛迭代（1000总迭代）。 在以下代码段中声明了相应的值：

nb_iterations = 1000 nb_adj_iterations = 500

在这一点上，我们可以基于差值w-x的 L2 范数定义权重矩阵（初始化为w[ij] ~ N(0, 0.01)）和负责计算获胜单元的函数，如下所示：

import numpy as np

pattern_length = 64 * 64 pattern_width = pattern_height = 64  matrix_side = 8 
W = np.random.normal(0, 0.1, size=(matrix_side, matrix_side, pattern_length))

def winning_unit(xt):
    distances = np.linalg.norm(W - xt, ord=2, axis=2)
    max_activation_unit = np.argmax(distances)
    return int(np.floor(max_activation_unit / matrix_side)), max_activation_unit % matrix_side

在开始训练周期之前，预先计算距离矩阵dm(x[0], y[0], x[1], y[1])，其中每个元素代表(x[0], y[0])和(x[1], y[1])。 如以下片段所示，此步骤避免了必须确定获胜单元的邻域时的计算开销：

import numpy as np

precomputed_distances = np.zeros((matrix_side, matrix_side, matrix_side, matrix_side))

for i in range(matrix_side):
    for j in range(matrix_side):
        for k in range(matrix_side):
            for t in range(matrix_side):
                precomputed_distances[i, j, k, t] = \
                    np.power(float(i) - float(k), 2) + np.power(float(j) - float(t), 2)

def distance_matrix(xt, yt, sigmat):
    dm = precomputed_distances[xt, yt, :, :]
    de = 2.0 * np.power(sigmat, 2)
    return np.exp(-dm / de)

函数distance_matrix()计算一个正方形矩阵，该正方形矩阵包含所有以(xt, yt)为中心的神经元的指数衰减影响。 现在，我们具有创建训练过程所需的所有构造块，该训练过程基于我们先前描述的权重更新规则，如下所示：

import numpy as np

sequence = np.arange(0, X.shape[0])
t = 0

for e in range(nb_iterations):
    np.random.shuffle(sequence)
    t += 1

    if e < nb_adj_iterations:
        etat = eta(t)
        sigmat = sigma(t)
    else:
        etat = 0.2
        sigmat = 1.0

    for n in sequence:
        x_sample = X[n]

        xw, yw = winning_unit(x_sample)
        dm = distance_matrix(xw, yw, sigmat)

        dW = etat * np.expand_dims(dm, axis=2) * (x_sample - W)
        W += dW

    W /= np.linalg.norm(W, axis=2).reshape((matrix_side, matrix_side, 1))

    if e > 0 and e % 100 == 0:
        print('Training step: {}'.format(t-1))

在每个循环中，执行以下步骤：

1. 为了避免相互关联，对输入样本的顺序进行了混洗。
2. 计算学习率和距离方差（收敛值为η[∞] = 0.2和σ[∞] = 1）。
3. 对于每个样本，适用以下条件：
   1. 计算获胜单元。
   2. 计算距离矩阵。
   3. 计算和应用权重更新。
4. 权重被重新归一化，以避免溢出。

现在，我们可以在训练过程结束时显示权重矩阵，如下所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RgQiCLrz-1681652675181)(https://gitcode.net/apachecn/apachecn-dl-zh/-/raw/master/docs/handson-unsup-learn-py/img/88ce6334-3cd3-41c5-a1de-9885b75dde3f.png)]

训练过程结束时的 Kohonen 映射权重矩阵

可以看到，每个权重都集中在人脸的通用结构上（因为数据集仅包含这种模式）； 但是，不同的权重已变得对特定的输入属性更敏感。 我建议您开始观察左上脸的元素（例如，眼睛或嘴巴），然后沿终止于中央砝码的螺旋线沿顺时针方向旋转。 这样，很容易看到接收字段中的修改。 作为练习，我邀请读者使用其他数据集（例如 MNIST 或 Fashion MNIST）测试模型，并对最终权重矩阵进行手动标记（例如，考虑到此示例，特定权重可以表示笑脸） 戴着眼镜，大鼻子）。 在标记每个元素之后，可以通过直接提供标记作为输出来投影原始样本并检查哪些神经元更易接受。

总结

在本章中，我们介绍了 GAN 的概念，并讨论了 DCGAN 的示例。 这种模型具有通过使用 minimax 游戏中涉及的两个神经网络来学习数据生成过程的能力。 生成器必须学习如何返回与训练过程中使用的其他样本没有区别的样本。 判别者或批评者必须变得越来越聪明，只为有效样本分配高概率。 对抗训练方法的基础是，通过学习如何用具有与真实属性相同的合成样本作弊的方法，迫使生成器与判别器竞争。 同时，生成器被迫通过选择越来越多来与歧视者抗争。 在我们的示例中，我们还分析了一个称为 WGAN 的重要变体，当标准模型无法复制有效样本时可以使用该变体。

SOM 是基于大脑特定区域功能的结构，该结构迫使其特定单元学习输入样本的特定特征。 这样的模型会自动进行自我组织，从而使响应相似模式的单元更加接近。 一旦提供了一个新样本，就足以计算获胜单元，该单元的权重与样本的距离最短； 并且在贴标过程之后，可以立即了解引起响应的特征（例如，垂直线或高级特征，例如是否有眼镜或胡须或人脸形状）。

问题

1. 在 GAN 中，生成器和判别器的作用与自编码器中的编码器和解码器相同。 它是否正确？
2. 判别器能否输出(-1, 1)范围内的值？
3. GAN 的问题之一是判别器过早收敛。 这个正确吗？
4. 在 Wasserstein GAN 中，批评家（区分者）在训练阶段是否比生成器慢？
5. 考虑到前面的问题，不同速度的原因是什么？
6. U(-1, 0)和U(1, 2)之间的 Jensen-Shannon 散度值是多少？
7. 赢家通吃战略的目标是什么？
8. SOM 训练过程的调整阶段的目的是什么？

进一步阅读

• Generative Adversarial Networks, Goodfellow I. J., Pouget-Abadie J., Mirza M., Xu B., Warde-Farley D., Ozair S., Courville A., and Bengio Y., arXiv:1406.2661 [stat.ML]
• Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks, Radford A., Metz L., and Chintala S., arXiv:1511.06434 [cs.LG]
• Wasserstein GAN, Arjovsky M., Chintala S., and Bottou L., arXiv:1701.07875 [stat.ML]
• How Patterned Neural Connections Can Be Set Up by Self-Organization, Willshaw, D. J. and Von Der Malsburg, C., Proceedings of the Royal Society of London, B/194, N. 1117, 1976
• Self-Organized Formation of Topologically Correct Feature Maps, Kohonen T., Biological Cybernetics, 43/1, 1982
• Mastering Machine Learning Algorithms, Bonaccorso G., Packt Publishing, 2018

十、习题

第一章

1. 无监督学习可以独立于有监督的方法应用，因为其目标是不同的。 如果问题需要监督的方法，则通常不能采用无监督的学习作为替代解决方案。 通常，无监督方法尝试从数据集中提取信息片段（例如，聚类）而没有任何外部提示（例如预测错误）。 相反，受监督的方法需要提示才能更正其参数。

2. 由于目标是找到趋势的原因，因此有必要执行诊断分析。

3. 否; 从单个分布中提取n个独立样本的可能性作为单个概率的乘积（主要假设请参见问题 4）。

4. 主要假设是样本是独立同分布（IID）的。

5. 性别可以编码为数字特征（例如，单热编码）； 因此，我们需要考虑两种可能性。 如果在属性之间不存在性别，而其他特征与性别不相关，则聚类结果是完全合理的。 如果存在性别（作为通用聚类方法）是基于样本之间的相似性的，则 50/50 的结果表示性别不是歧视性特征。 换句话说，给定两个随机选择的样本，它们的相似性不受性别影响（或受到轻微影响），因为其他特征占主导。 例如，在这种特殊情况下，平均分数或年龄有较大的差异，因此它们的影响更大。

6. 我们可以预期会有更紧凑的群体，其中每个主要特征的范围都较小。 例如，一个小组可以包含 13-15 岁的学生，并带有所有可能的分数，依此类推。 另外，我们可以观察基于单个特征的细分（例如年龄，平均分数等）。 最终结果取决于向量的数值结构，距离函数，当然还取决于算法。

7. 如果每个客户均由包含其兴趣摘要的特征向量表示（例如，基于他/她购买或看过的产品），我们可以找到集群分配，检查哪些元素可以表征集群（例如书籍，电影，衣服，特定品牌等），并使用这些信息来推荐潜在产品（即类似用户购买的产品）。 该概念基于在相同集群的成员之间共享信息的主要思想，这要归功于它们的相似性。

第二章

1. 曼哈顿距离与 Minkowski 距离相同，其中p = 1； 因此，我们希望观察到更长的距离。

2. 否; 收敛速度主要受质心的初始位置影响。

3. 是; K 均值设计用于凸群集，而对于凹群集则表现较差。

4. 这意味着所有聚类（样本百分比可忽略不计）分别仅包含属于同一类别（即具有相同真实标签）的样本。

5. 它表示真实标签分配和分配之间的中等/强烈的负差异。 这个值是明显的负条件，不能接受，因为绝大多数样本已分配给错误的聚类。

6. 不可以，因为调整后的 Rand 分数是根据真实情况得出的（也就是说，预期的群集数是固定的）。

7. 如果所有基本查询都需要相同的时间，则会在60 - (2×4) - 2 = 50秒内执行它们。 因此，它们每个都需要50/100 = 0.5秒。 在叶子大小= 50的情况下，我们可以期望将 50-NN 查询的执行时间减半，而对基本查询没有影响。 因此，可用于基本查询的总时间变为60 - (2×2) - 2 = 54秒。 因此，我们可以执行 108 个基本查询。

8. 否; 球树是一种不会遭受维度诅咒的数据结构，其计算复杂度始终为O(N log M)。

9. 高斯N([-1.0, 0.0], diag[0.1, 0.2])和N([-0.8, 0.0], diag[0.3, 0.3])重叠（即使所得聚类非常伸展），而第三个则足够远（考虑均值和方差），可以被单独的聚类捕获。 因此，最佳群集大小为 2，而 K 均值很难将大斑点正确地分为两个内聚分量（特别是对于大量样本）。

10. VQ 是一种有损压缩方法。 仅当语义没有通过小或中转换而改变时，才可以使用它。 在这种情况下，如果不修改基础语义就不可能与另一个交换令牌。

第三章

1. 否; 在凸集中，给定两个点，连接它们的线段始终位于该集内。
2. 考虑到数据集的径向结构，RBF 内核通常可以解决该问题。
3. 在ε = 1.0的情况下，许多点无法达到密度。 当球的半径减小时，我们应该期望有更多的噪点。
4. 否; K 中心点可以采用任何度量。
5. 否; DBSCAN 对几何不敏感，并且可以管理任何种类的群集结构。
6. 我们已经表明，小批量 K 均值的表现稍差于 K 均值。 因此，答案是肯定的。 使用批量算法可以节省内存。
7. 考虑到噪声的方差为σ^2 = 0.005 → σ ≈ 0.07，它比聚类标准差小约 14 倍，因此，我们不能期望这么多的新分配（80%）在稳定的群集配置中。

第四章

1. 在凝聚方法中，该算法从每个样本（被视为一个集群）开始，然后继续合并子集群，直到定义了一个集群。 在分裂方法中，该算法从包含所有样本的单个群集开始，然后通过拆分将其进行到每个样本组成一个群集为止。

2. 最近的点是(0, 0)和(0, 1)，因此单键是L[s](a, b) = 1。 最远的点是(-1, -1)和(1, 1)，因此完整的链接是L[c(a, b) = 2√2。

3. 否; 树状图是给定度量和链接的层次聚类过程的树表示。

4. 在凝聚聚类中，树状图的初始部分包含所有样本作为自治聚类。

5. y轴报告差异。

6. 将较小的群集合并为较大的群集时，差异性会增加。

7. 是; 那就是 cophenetic 矩阵的定义。

8. 连通性约束允许施加约束，因此将约束合并到聚合过程中，从而迫使其将某些元素保留在同一群集中。

第五章

1. 硬聚类基于固定分配； 因此，样本x[i]将始终属于单个群集。 相反，相对于每个聚类，软聚类返回一个度向量，该向量的元素表示隶属度（例如，（0.1、0.7、0.05、0.15））。
2. 否; 模糊 c 均值是 K 均值的扩展，它不适用于非凸几何。 但是，软分配可以评估相邻群集的影响。
3. 主要假设是，数据集是从可以用多个高斯分布的加权和有效地近似的分布中得出的。
4. 这意味着第一个模型的参数数量是第二个模型的两倍。
5. 第二个是因为它可以用更少的参数实现相同的结果。
6. 因为我们要为组件的自动选择采用这种模型。 这意味着我们要从更大数量的权重开始，期望它们中的许多权重将被迫接近 0。由于 Dirichlet 分布具有非常稀疏的性质并且适用于单纯形，因此，这是最佳的选择。 先验。
7. 如果它们是从相同的来源收集的，并且已验证标记的来源，我们可以采用半监督方法（例如，生成高斯混合物），以便为其余样本找到最合适的标记。

第六章

1. 由于随机变量显然是独立的，因此P(Tall, Rain) = P(Tall)P(Rain) = 0.75 * 0.2 = 0.15。
2. 直方图的主要缺点之一是，当桶的数量太大时，它们中的许多都开始为空，因为在所有值范围内都没有样本。 在这种情况下，X的基数可以小于 1,000，或者即使具有超过 1,000 个样本，相对频率也可以集中在小于 1,000 的多个桶中。
3. 样本总数为 75，并且各个条带的长度相等。 因此， P(0 < x < 2) = 20/75 ≈ 0.27，P(2 < x < 4) = 30/75 = 0.4和P(4 < x < 6) = 25/75 ≈ 0.33。 由于我们没有任何样本，因此我们可以假设P(x > 6) = 0； 因此，P(x > 2) = P(2 < x < 4) + P(4 < x < 6) ≈ 0.73。 考虑到0.73•75 ≈ 55，这是属于x > 2的桶的样本数，我们立即得到确认。
4. 在正态分布N(0, 1)中，最大密度为p(0) ≈ 0.4。 在大约三个标准差之后，p(x) ≈ 0； 因此，通常无法将样本p(x) = 0.35的样本x视为异常。
5. 当min(std(X), IQR(X) /1.34) ≈ 2.24时，最佳带宽为h = 0.9•2.24•500^(-0.2) = 0.58。
6. 即使可以采用高斯核，在给出分布描述的情况下，我们也应首先选择指数核，这样可以使均值周围迅速下降。
7. 这将是最合乎逻辑的结论。 实际上，就新颖性而言，我们也应该期望新样本会改变分布，以便为新颖性建模。 如果在重新训练模型后概率密度仍然很低，则样本很可能是异常的。

第七章

1. 协方差矩阵已经是对角线； 因此，特征向量是标准x和y，分别为(1, 0)和(0, 1)，特征值是 2 和 1。因此，x轴是主要成分，y轴是第二个成分。

2. 由于球B[0.5](0, 0)是空的，因此在该点(0, 0)周围没有样本。 考虑到水平方差σ[x]^2 = 2，我们可以想象X被分解为两个斑点，因此可以想象x = 0行是水平判别器。 但是，这只是一个假设，需要使用实际数据进行验证。

3. 不，他们不是。 PCA 之后的协方差矩阵不相关，但不能保证统计独立性。

4. 是; Kurt(X)的分布是超高斯分布，因此达到峰值且尾巴很重。 这样可以保证找到独立的组件。

5. 由于X包含负数，因此无法使用 NNMF 算法。

6. 否; 由于字典有 10 个元素，因此意味着文档由许多重复出现的项目组成，因此字典不够完整（ 10 < 30）。

7. 样本(x, y) ∈ R^2通过二次多项式变换为(ax, by, cx^2, dy^2, exy, f) ∈ R^6。

第八章

1. 不，他们没有。 编码器和解码器都必须在功能上对称，但是它们的内部结构也可以不同。
2. 否; 输入信息的一部分在转换过程中丢失，而其余部分则在代码输出Y和自编码器变量之间分配，该变量与基础模型一起对所有转换进行编码。
3. 当min(sum(z[i]))= 0和min(sum(z[i]))= 128时，等于 36 的总和既可以表示稀疏（如果标准差较大），也可以表示具有较小值的均匀分布（当标准差接近零时）。
4. 当sum(z[i]) = 36时，std(z[i]) = 0.03意味着大多数值都围绕0.28 * (0.25÷0.31)，该代码可以视为密集代码。
5. 否; 一个 Sanger 网络（以及 Rubner-Tavan 网络）需要输入样本x[i] ∈X。
6. 从最大特征值到最小特征值（即从第一个主成分到最后一个主成分）以降序提取成分。 因此，无需进一步分析来确定其重要性。
7. 是; 从最后一层开始，可以对每个内部层的值进行采样，直到第一层为止。 通过选择每个概率向量的argmax(·)获得最可能的输入值。

第九章

1. 否; 生成器和判别器在功能上是不同的。
2. 不，不是这样，因为判别器的输出必须是一个概率（即p[i] ∈ (0, 1)）。
3. 是; 这是正确的。 判别器可以学习非常快地输出不同的概率，，其损失函数的斜率可以变得接近于 0，从而减小了提供给生成器的校正反馈的幅度。
4. 是; 通常会比较慢。
5. 评论者比较慢，因为每次更新后都会对变量进行裁剪。
6. 由于支撑脱节，Jensen-Shannon 散度等于log(2)。
7. 目标是开发高度选择性的单元，其响应仅由特定特征集引起。
8. 在训练过程的早期阶段，不可能知道最终的组织。 因此，强制某些单元的过早专业化不是一个好习惯。 调整阶段允许许多神经元成为候选神经元，与此同时，逐渐增加最有前途的神经元（将成为赢家）的选择性。