python笔记（四）之科学计算模块、创建数组、Numpy数组的性质、数组的索引、数组切片（获取子数组）、副本与视图、数组的变形、数组的拼接与分裂、数组运算、对比操作、数组排序

python科学计算模块库

SciPy是一个基于Python的开放源码软件生态系统来服务于数学、科学和工程。特别是，这些是一些核心软件包：

NumPY

围绕矩阵和数组的操作。
数据类型：
Bool
Int
float
complex

数组属性：
ndarray.ndim
ndarray.shape
…

数组操作：
NumPy创建数组
NumPy切片和索引
NumPy数组操作
NumPy字符串函数
NumPy数学函数

SciPy library

MatPlotlib

IPython

SymPy

符号运算

pandas

excel操作需要该库。
Pandas是一个开放源码的Python库，它使用强大的数据结构提供高性能的数据操作和分析工具。

每一个库都对应不同的数据类型，所以我们在使用之前需要知道我们的数据是什么类型的。

注：当我们拥有软件Anaconda的时候导入其python.exe多半这些库以及加载了，可以在CMD处输入pip list 查看是否有这些包。

这些包如何使用呢？
登录官网，查看官方文档。

列表创建数组

A = np.array([1, 4, 2, 5, 3])#方括号括起来说明这是一个列表，一个list
print(A)
print(type(A))

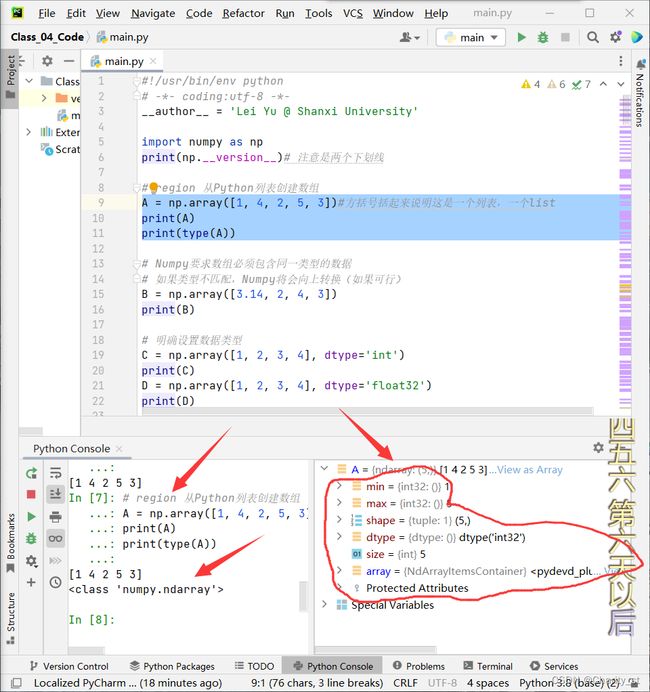
注意这里的A是一个ndarray类型，里面的最小值最大值等等多已计算好了。

# region 从Python列表创建数组
A = np.array([1, 4, 2, 5, 3])#方括号括起来说明这是一个列表，一个list
print(A)
print(type(A))

# Numpy要求数组必须包含同一类型的数据
# 如果类型不匹配，Numpy将会向上转换（如果可行）
B = np.array([3.14, 2, 4, 3])#强制把整数型的2 3 4 转换为浮点型，为保证数据不丢失，向上转换，而不是把3.14转换为int
print(B)

# 明确设置数据类型
C = np.array([1, 2, 3, 4], dtype='int')
print(C)
D = np.array([1, 2, 3, 4], dtype='float32')
print(D)

# 初始化多维数组
E = np.array([range(i, i+3) for i in [2, 4, 6]])#range后面的（）是一个左闭右开的区间
#这样的写法并不直观，可读性较差
print(E)
# endregion

从头创建数组

numpy里面可以帮助我们创建很多特殊的数组。

全0数组

A = np.zeros(10, dtype=int)
print(A)

全1数组

# 全1数组
B = np.ones((3, 5), dtype=float)#3行5列，是一个元组，创建的参数，而不是两个单独的数
print(B)
C = np.full((3, 5), 3.14)#创建一个3行5列的数组，里面每一个元素都是3.14
print(C)

线性序列数组

# 线性序列数组
D = np.arange(0, 20, 2)#0~20，间隔是2，等差数列
print(D)

随机数组

# 随机数组
D = np.random.choice(2, 20, replace=True)#随机分布，2：我产生随机数范围为0~2又因为是左闭右开，所以也就是0、1
#20：表示产生20个随机数，replace：表示概率论的表示有放回的抽样，特征选择时候会用到
print(D)

0-1区间均匀数组

# 0～1区间的均匀数组
E = np.linspace(0, 1, 5)#均匀产生随机数，0-1均匀产生5个随机数（既包括0也包括1，随机数可以是浮点型）
print(E)
#结果为[0.   0.25 0.5  0.75 1.  ]#四等分
# 3*3的、在0～1均匀分布的随机数组
F = np.random.random((3, 3))
print(F)

正态分布随机数组

# 3*3的、均值为0、标准差为1的正态分布随机数组
G = np.random.normal(0, 1, (3, 3))
print(G)

随机整型数组

# 3*3的，[0, 10)区间的随机整型数组
H = np.random.randint(0, 10, (3, 3))#注意这里是整数
print(H)

单位矩阵

# 3*3的单位矩阵
I = np.eye(3)
print(I)

Numpy数组的性质

np.random.seed(0)
这里（）里是一个整数即可，保证程序每次运行随机数是一样的，要不然每次程序运行效果是不同的。

np.random.seed(0)# 随机数发射种子，（）里是一个整数即可，保证程序每次运行随机数是一样的，要不然每次程序运行效果是不同的
x1 = np.random.randint(10, size=6)#randint 产生随机整数的矩阵
x2 = np.random.randint(10, size=(3, 4))#产生三行四列的矩阵
x3 = np.random.randint(10, size=(3, 4, 5))#可以产生3维矩阵
print("x1 = ", x1)
print("x2 = ", x2)
print("x3 = ", x3)

ndarray类型数据,则可以运行下面指令，有助于图像处理时候的应用。

#x3是一个ndarray,则可以运行下面指令，有助于图像处理时候的应用
print("x3 ndim: ", x3.ndim)#显示是几维矩阵
print("x3 shape: ", x3.shape)#显示是矩阵大小
print("x3 size: ", x3.size)#显示是矩阵有多少元素
print("x3 dtype: ", x3.dtype)#显示类型
print("x3 itemsize: ", x3.itemsize, "bytes")#显示每一个元素占多少个字节
print("nbytes: ", x3.nbytes, "bytes")#显示是整个矩阵占多大内存
# endregion

数组的索引

单个元素

方括号获取指定索引的值（下标从0开始）

# 方括号获取指定索引的值（下标从0开始）
x = np.array([5, 0, 3, 7, 9])#注意是方括号、且从0开始，五个元素，索引是0~4
print(x[0])
print(x[4])

获取数组的末尾元素

print(x[-1])#倒数第一个元素
print(x[-2])#倒数第二个元素

多维数组

多维数组中，用逗号分隔的索引元组获取元素。

y = np.array([[3, 5, 2, 4],
              [7, 6, 8, 1],
              [0, 9, 3, 2]])
print(y[0, 0])#打印结果为3
print(y[1, 2])#第2行第2列的元素 第一行用0表示
print(y[2, -1])

注意：print(y[1, 2])#第2行第2列的元素 第一行用0表示。

用索引方式修改元素值

y[0, 0] = 5
print(y)

y[0, 0] = 3.9415926
print(y)#做了四舍五入的取整，因为这个数组创建时候是整型，注意是向下取整

注意：当数组是int时候，当我们令元素为float，则会向下取整。
这里后面输出的第一个元素是3，而不是4。

数组切片：获取子数组

一维子数组的获取

# 一维子数组
x = np.arange(10)
print(x)
print(x[:5])    # 前5个元素
print(x[5:])    # 索引5之后的元素
print(x[4:7])   # 索引4～7之间的子数组
print(x[::2])   # 每隔一个元素，即间隔为2
print(x[1::2])  # 每隔一个元素，从索引1开始
print(x[::-1])  # 所有元素，逆序
print(x[5::-2]) # 从索引5开始，每隔一个元素，逆序

二维子数组的获取

# 多维子数组
y = np.random.randint(0, 10, (3, 4))
print(y)
print(y[:2, :3])        # 前两行，前三列
print(y[:3, ::2])       # 所有行，每隔一列
print(y[::-1, ::-1])    # 行列同时，逆序
print(y[0, :])           # 第一行
print(y[0])
print(y[:, 0])           # 第一列

副本与视图

这里的副本与视图总让我怀念当时学C、C++的日子。
视图类似于传参时候是用了指针，指向了同一个地址，所以我们修改视图时候，原来的参数值也改变了。
副本则是指传递了数值，而非地址，所以修改不影响原来参数。

# 副本与视图
y = np.random.randint(0, 10, (3, 4))
print(y)
y_sub = y[:2, :2]       # y_sub是y的视图
y_sub[0, 0] = 99        # 修改y_sub中元素的值后，y中的值也被改变
print(y)
#这里的y_sub是y的一个视图，他们指向的地址是相同的

y = np.random.randint(0, 10, (3, 4))
print(y)
y_sub_copy = y[:2, :2].copy()   # y_sub_copy是y的副本
y_sub_copy[0, 0] = 99           # 修改y_sub_copy中元素的值后，y中的值不受影响
print(y_sub_copy)
print(y)
#副本则不会改变原来的值

# endregion

数组的变形

python里默认的reshape是行优先。有的语言默认的是列有限。

A = np.arange(1, 10)#1~9
B = A.reshape((3, 3))#变成3*3的矩阵，这里默认行优先
print(A)
print(B)

A：

[1 2 3 4 5 6 7 8 9]

B:

[[1 2 3]
 [4 5 6]
 [7 8 9]]

一维数组转换成二维的行或列矩阵

x = np.array([1, 2, 3])
print(x)
print(x.shape)
y = x.reshape((1, 3))
print(y)
print(y.shape)#做拼接之前有时候需要进行转换
z = x[np.newaxis, :]#升维操作
print(z)
print(z.shape)

a = x.reshape((3, 1))
b = x[:, np.newaxis]
print(a)
print(a.shape)
print(b)
print(b.shape)

结果：

[1 2 3]
(3,)
[[1 2 3]]
(1, 3)
[[1 2 3]]
(1, 3)
[[1]
 [2]
 [3]]
(3, 1)
[[1]
 [2]
 [3]]
(3, 1)

数组的拼接与分裂

一维数组的拼接

一维的时候concatenate是水平拼接，即左右。

# 一维数组的拼接
#垂直的拼接 上下 还是水平方向的拼接 左右
x = np.array([1, 2, 3])
y = np.array([3, 2, 1])
#一维的时候concatenate是水平拼接 左右
z = np.concatenate([x, y])
print(z)
print(np.concatenate([x, y, z]))

结果：

[1 2 3 3 2 1]
[1 2 3 3 2 1 1 2 3 3 2 1]

二维数组的拼接

# 二维数组的拼接
A = np.random.randint(0, 10, (2, 4))
print("A = \n", A)
B = np.random.randint(0, 10, (2, 4))
print("B = \n", B)

#区分：一维的时候concatenate是水平拼接 左右
C = np.concatenate([A, B])          # 按行的方向拼接 上下拼接
C = np.concatenate([A, B], axis=0)#axis设置拼接方式，0：垂直方向，1：水平方向
C = np.vstack([A, B]) #垂直方向拼接
#上述三行代码功能一样
print("C = \n", C)

D = np.concatenate([A, B], axis=1)  # 按列的方向拼接 左右
D = np.hstack([A, B])#水平拼接
print("D = \n", D)

数组的分裂

一维数组的分裂

# 一维数组的分裂
x = [1, 2, 3, 7, 4, 6, 9, 5, 0]
print(x)
x1, x2, x3 = np.split(x, [3, 5])
print(x1)
print(x2)
print(x3)

二维数组的分裂

# 二维数组的分裂
#要清楚水平方向上去做分裂还是垂直方向
A = np.random.randint(0, 10, [3, 5])
print(A)
B, C = np.vsplit(A, [1])#垂直方向 从第一行处开始分 即按行分
print(B)
print(C)

D, E = np.hsplit(A, [3])#水平方向 按列分，从第三列开始分
print(D)
print(E)

数组的运算

加减乘除

# region 数组的运算
x = np.arange(4)
print("x = ", x)
print("x + 5 = ", x + 5)                # np.add(x, 5)
print("x - 5 = ", x - 5)                # np.subtract(x, 5)
print("x * 2 = ", x * 2)                # np.multiply(x, 2)
print("x / 2 = ", x / 2)                # np.divide(x, 2)

向下取整、取反、指数、模

print("x // 2 = ", x // 2)  # 向下整除  # np.floor_divide(x, 2)
print("-x = ", -x)                      # np.negative(x)
print("x ** 2 = ", x ** 2)  # 指数      # np.power(x, 2)
print("x % 2 = ", x % 2)    # 模         # np.mod(x, 2)

绝对值（多个函数都可以实现该功能）

print(abs(x))       # 绝对值，多个函数都可以实现该功能
print(np.abs(x))
print(np.absolute(x))

三角函数

theta = np.linspace(0, np.pi, 3)    # 三角函数
print("theta = ", theta)
print("sin(theta) = ", np.sin(theta))       # np.arcsin(x)
print("cos(theta) = ", np.cos(theta))       # np.arccos(x)
print("tan(theta) = ", np.tan(theta))       # np.arctan(x)

指数和对数

x = [1, 2, 3]       # 指数和对数
print("e^x = ", np.exp(x))          # np.log(x)
print("2^x = ", np.exp2(x))         # np.log2(x)
print("3^x = ", np.power(3, x))     # np.log10(x)

对整个矩阵的统计运算

#对整个矩阵统计运算的函数
L = np.random.randint(0, 10, (3, 5))
print("L = \n", L)
print("sum(L) = ", np.sum(L))       # 求和
print(np.sum(L, axis=0))
print(np.sum(L, axis=1))


print("min(L) = ", np.min(L))       # 最小值
print(np.min(L, axis=0))
print(np.min(L, axis=1))

print("max(L) = ", np.max(L))       # 最大值
print(np.max(L, axis=0))
print(np.max(L, axis=1))

#知道最大值、最小值，有利于变量的归一化

对比操作

# region 比较操作
x = np.array([1, 4, 5, 3, 6, 2])

print(x > 3)                    # 大于
print("x > 3: ", x[x > 3])#索引可以是一个数值，逻辑型的也可以作为一个索引

print(x >= 3)                    # 大于等于
print("x >= 3: ", x[x >= 3])

print(x < 3)                    # 小于
print("x < 3: ", x[x < 3])

print(x <= 3)                    # 小于等于
print("x <= 3: ", x[x <= 3])

print(x == 3)                   # 等于
print("x == 3: ", x[x == 3])

print(x != 3)                   # 不等于
print("x != 3: ", x[x != 3])#matlab里是~=

# 统计记录的个数
print(np.count_nonzero(x > 3))#数非0元素的个数
print(np.sum(x > 3))

# 检查是否满足特定条件
print(np.any(x > 4))
print(np.all(x > 4))#每一个都要满足

# 布尔运算符
x = np.array([1, 4, 5, 3, 6, 2])
print(np.sum((x > 1) & (x < 5)))
print(np.sum((x < 1) | (x > 5)))
print(np.sum(~((x <= 1) | (x >= 5))))

# endregion

数组排序

# region 数组排序
x = np.array([2, 1, 4, 3, 5])
# print(np.sort(x))
x.sort()#默认是升序
print(x)
#sort()还有另外一个关键字参数，就是reverse，它是一个布尔值True/False，作用是用来决定是否要对列表进行反向排序。


x = np.array([2, 1, 4, 3, 5])
i = np.argsort(x)               # 排序索引值,按值的大小，把索引值进行排序
print(i)
# endregion

#机器学习可以有很多包，进行照猫画虎，如scikit-learn
#一个模型2-3行代码即可构建
#进阶：在底层源代码层面进行学习
#