【研究型论文】EC-GCN: A encrypted traffic classification framework based on multi-scale GNN

EC-GCN: A encrypted traffic classification framework based on multi-scale graph convolution networks

中文题目：EC-GCN:一种基于多尺度图卷积网络的加密流分类框架
发表期刊：Computer Networks
发表年份：2023 / 3
作者：Zulong Diao, Gaogang Xie, Xin Wang, Rui Ren, Xuying Meng, Guangxing Zhang, Kun Xie, Mingyu Qiao
latex引用：

@article{diao2023ec,
  title={EC-GCN: A encrypted traffic classification framework based on multi-scale graph convolution networks},
  author={Diao, Zulong and Xie, Gaogang and Wang, Xin and Ren, Rui and Meng, Xuying and Zhang, Guangxing and Xie, Kun and Qiao, Mingyu},
  journal={Computer Networks},
  volume={224},
  pages={109614},
  year={2023},
  publisher={Elsevier}
}

摘要

加密流量的急剧增长给传统的流量分类方法带来了巨大的挑战。将深度学习与时间序列分析技术相结合是解决这一问题的最新趋势。这些方法大多只捕获流中的时间相关性。精度和鲁棒性不理想，特别是在不稳定的网络环境，容易出现高丢包和重排序的问题。如何为每一个加密流量学习一个具有较强泛化能力的表示仍然是一个关键的挑战。我们的详细分析表明，存在一个具有特定局部结构的图，对应于每种类型的加密流量。受这一观察结果的启发，我们提出了一种新的深度学习框架EC-GCN，用于对基于多尺度图卷积神经网络的加密交通流进行分类。

我们首先提供了一个新的轻量级层，它只依赖于元数据，并将每个加密的流量编码为图形表示。因此我们的框架可以独立于不同的加密协议。然后设计了一种新的图池化层和结构学习层，动态提取多图表示，提高了适应复杂网络环境的能力。EC-GCN是一种端到端分类模型，它学习隐藏在流量时间序列中的代表性时空流量特征，然后在统一的框架中对其进行分类。我们在三个真实数据集上的综合实验表明，EC-GCN可以实现高达5%-20%的精度提高，优于最先进的方法。

存在的问题

1. 与以前的方法相比，端到端模型的可用信息有限。大多数算法只提取时间序列内的时间相关性，导致分类精度和适应性较低。
2. 由于不同网络位置的流量分布不同，这些方法的性能也不同。
3. 此外，由于网络故障，加密流量数据的实时报文长度序列可能会出现部分异常(丢包/重排序)。由于连续报文之间的时间间隔的变化，流量的多次聚合也会对模型的性能产生很大的影响。

论文贡献

1. 将加密流量表示为图形，并观察到许多明显的特征，这些特征揭示了加密流量中的潜在空间模式。
2. 为了了解隐藏在流中的空间依赖性，我们创造性地将GCN引入我们的分类方法中，并提出了一种新的时间-空间(多子图)加密流量分类框架。据我们所知，这是第一个用于对加密流量进行分类的基于多图的方法。为了使我们的方法对噪声和动态具有鲁棒性，我们将图组织成多个粒度级别，并利用所有级别的特征。
3. 在深度学习框架中，我们创造性地设计了一个编码层，以自动将加密的流量转换为图形表示。此外，我们还提出了一种新的图形化层和图形学习层来动态提取加密流量中的多图结构。
4. 为了评估我们提出的模型的性能，我们在3个数据集上进行了一系列实验。实验结果表明，与现有方法相比，EC-GCN算法的精度提高了5% ~ 20%，容错能力更强。

论文解决上述问题的方法：

1. 将加密流量表示为图形，并观察到许多明显的特征，这些特征揭示了加密流量中的潜在空间模式。使用GCN来提取空间特征。
2. 为了使提出的方法对噪声和动态具有鲁棒性，将图组织成了多个粒度级别，并利用所有级别的特征。

论文的任务：

以报文长度序列为输入，将加密后的流量分类到特定的应用中

1. 分析和动机

图结构分析

为了可视化网络流量流中的图表示，对流量进行了构图，具体方法如下：

• 图节点：

  数据包长度的状态（从0到最大传输单元MTU）

• 图的边

  将边定义为两个节点之间的关联（与同一流量中两个对应数据包长度之间的转移概率直接相关）

• 图构建：

  1. 从每个流量中选取前 $M$ 个连续报文，形成时间序列。
  2. 根据每个流量的包长度序列计算转换矩阵 $TM\in R^{MTU\times MTU}$，$T{M}_{i,j}$表示从节点 $i$ 到节点 $j$ 的转移数值。
  3. 然后为了分析不同web应用的图结构，直接将相同应用的所有转移矩阵相加。
  4. 如果转换矩阵中对应的项小于某个阈值（证明在这个web应用中，数据包长度1转移到数据包长度2的概率很小），则删除边。
  5. 如下图所示，不同的图号（从1到30）代表不同的web应用，图中不同的节点颜色代表不同的数据包长度间隔。加权度越大，对应图节点在流中出现的频率越高。
     
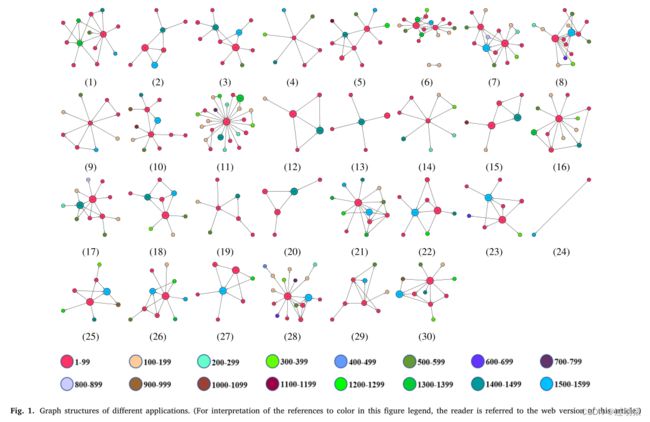
     从上图（上图中每个节点上标上了数据包大小，需要放大观看）可以看出以下几个特点：

  • 不同的web应用显示不同的图形拓扑，如图3、9、13、14中的星形拓扑，图1、8中的双核拓扑，图6中的多子图拓扑。这一现象表明，不同的web应用程序的通信方式存在明显的差异。
  • 不同的web应用具有不同的核心图形节点，如图1中的54、1394，图5中的74、1494，图9中的66、1514。这一现象表明，图结构可以在一定程度上揭示不同web应用程序的ACK机制。
  • 类似的网络应用有一些共同的特点，比如图12、15中类似的菱形结构，对应的是使用相同操作系统OSX和浏览器Chrome的微信、爱奇艺。

图节点和边分析

由于数据包长度可能从0到MTU不等，如果我们将每个可能的数据包长度映射到流量流中的一个图节点，那么图中可能至少包含数千个节点。基于gcn的模型的执行复杂度与图的规模直接相关。随着图节点数量的增加，执行时间将大大增加，这将不利于在线流量分类任务。因此，我们在这一部分也进行了一些图节点分析工作，并探索了将GCN引入我们的流分类任务的可行性。

• 图的节点分析

  首先，我们绘制了所有web应用程序的数据包长度分布。如图2(a)所示，不同应用的包长呈长尾分布，少量包长覆盖了大部分比例。这一现象表明，一个流对应的实际图节点数量是有限的。
  

• 图的边分析

  如图2(b)所示，我们分析了不同应用在图中(对应于一个流)的平均节点度。发现图中的平均节点度在3.60到5.82之间。这一现象表明，一个流对应的实际图边数是有限的。
  

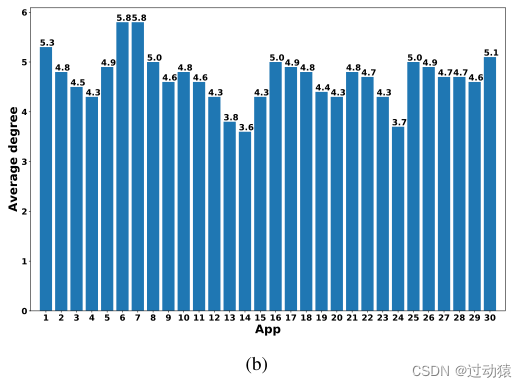
综上所述，我们可以得出结论，将GCN引入我们的在线流量分类任务中，采用有限尺度的图结构是可行的。

2. 问题和模型

问题定义

本文的加密流量分类问题：

输入：以报文长度序列
输出：将加密后的流量分类到特定的应用中

由于所有通信内容在加密后都是随机化的，因此我们不打算使用数据包有效载荷或报头中的任何内容。因此，我们唯一可以使用的信息是可以表示为时间序列的元数据。元数据包括数据包长度、数据包方向和到达时间。考虑到到达间时间常受网络环境影响，具有极不稳定的特性，我们只选择前两者，即（数据包长度，数据包方向）。

一些定义的符号：

• 应用数量：$T$
• 每个流提取的报文数量：前 $M$ 个
• 输入每个流的前 $M$ 个报文长度序列：$(x_1,x_2,...,x_M)$
• 流的分类标签：$Y_i，i\in [0,T)$

模型框架

仅依赖于相互流的元数据使我们的方法独立于加密协议细节。通过前面的分析，我们发现数据包长度序列既具有时间相关性（数据包长度随传输顺序而变化），也具有空间相关性（图形中的边）。

利用GCN，我们可以从高维的角度来处理加密流分类任务。然而，在设计一个新的基于图的分类模型时，我们仍然会面临严峻的挑战，需要找到以下问题的解决方案:

• 如何在相互流的元数据提供如此有限的信息的情况下实现性能改进?
• 如何将流量时间序列编码为GCN的图表示？
• 如何控制图的尺度以不影响在线分类的效率?

• 第1，2个问题：尝试基于GCN和每个流的互流元数据构建多级图表示，使我们能够从多维度和多尺度观察不同加密网络流的行为。
• 第3个问题：创造性地提出了独热层、轻量级图池层和结构学习层，以降低图表示学习的复杂性。

模型结构：

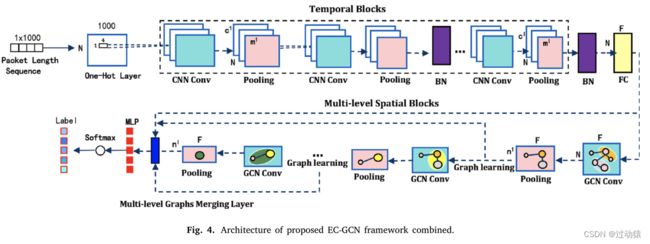
• 6个时间block：用于捕获时间相关性，并为图中的每个节点形成低维特征。
• 6层空间block：捕获不同层次的图形表示，然后以分层方式进行汇总。
• FC层：在时间块和空间块之间，我们增加了一个FC层，将所有通道的时间特征合并为每个节点的统一特征。

3. 工作流程

• 图表示：
  $$g=(v,\epsilon ,X,W)$$
  其中，$v$ 表示图中的节点； $\epsilon$表示图中的边；$X$ 表示图节点的特征矩阵， $W$ 表示图中边的权重矩阵。

  • 图节点：将0到MTU的报文长度范围平均划分为N个区间。每个区间代表一个图节点。
  • 边：两个图节点之间的对应关系

• 工作流程：

  下面举例说明整个图的构造流程：

  

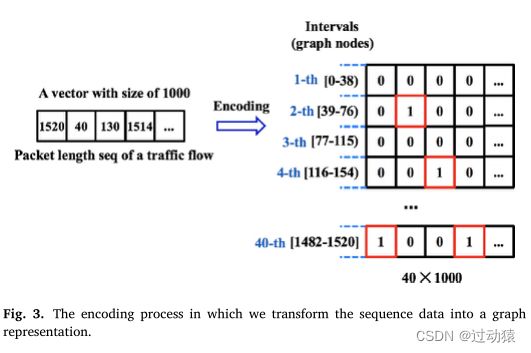
  1. 给定一个流，包含M（M=1000）个数据包，并且设定区间个数N=40
  2. 独热编码：以第一个大小为1520的报文为例，其间隔号为40。因此，第一列的第40位数字将被设置为1。这样一来，数据包序列就由原来的 $R^M$ 转为了 $R^{N\times M}$
  3. 将上面得到的独热编码矩阵对图节点的特征矩阵 $X$ 进行初始化，至此，我们在空间维度方向上得到了一个稀疏但线性独立的表示 $R^{N\times M\times 1}$（看作是batch_size * sequence_len * embedding_size）
  4. 通过6个时间块，将输入转换为隐藏表示 $H^{(l)}\in R^{N\times m^l\times c^l}$，其中 $m^l$ 是第 $l$ 个时间block的时间维度大小（即sequence_len），$c^l$ 是第 $l$ 个时间block的特征维度（即embedding_size）
  5. 然后我们附加一个全连接层(FC)，该层负责将来自所有通道的时间压缩特征合并为 $F$ 维统一空间特征。
  6. 通过6个时间快和全连接层后，特征维度从 $R^{N\times M\times 1}$ 转换成了 $R^{N\times F}$
  7. 得到节点的特征矩阵后，将图输入到6个空间块中，其中每个空间block包含一个GCN层和轻量级pooling层层
  8. 将每个空间block层得到的输出进行均值池化和最大池化，并将结果拼接在一起，送到MLP层对流进行分类。

• 模型创新：

  • The lightweight graph pooling layer（轻量级的图池化层）：
    为了提高模型的实时性，提出了一种轻量级的图池化层，从而在训练过程中逐层将图转化为一个规模更小的子图。具体实现方法如下：
    $$H^{(l+1)}=S^{(l)}{H}^{(l)}，其中H^{(l+1)}\in R^{n^{l+1}\times F}$$$$W^{(l+1)}=S^{(l)T}{W}^{(l)}{S}^{(l)}，其中W^{(l+1)}\in R^{n^{l+1}\times n^{l+1}}$$

  • 由于轻量级的图池化层可能会导致子图中高度相关的节点断开连接，从而失去图结构信息的完整性，进一步阻碍消息传递过程。因此单纯获得该层的权重矩阵 $W$ 还不够，还要对其进行一定程度的转换。方法如下：

  首先定义一个 $IR$
  $$IR=D^{(l)-1}{W}^{(l)}{H}^{(l)}，其中IR\in R^{n^l\times F}$$其中 $D^{(l)}$ 表示 $W^{(l)}$的对角度矩阵
  IR表示图中每个节点的交互得分，如果IR的某一行中的数值越大，就证明该节点（该行）与其余邻居节点交互越频繁。下面具体介绍当前 l 层的权重矩阵如何计算：
  

  • 合并层：
    对每个空间block的输出进行均值池化和max池化，并concat起来，然后将每个空间block池化后的结果相加，作为最终的图表示。

• 模型总结：

  输入层：

  • 输入：数据包序列，形状为[1, M], M为一个流中的数据包序列长度

  one-hot层：

  • 输入：数据包序列，形状为[1, M], M为一个流中的数据包序列长度
  • 输出：[N, M

  第 l 层时间block：

  • Conv1D、maxpooling：

  • 输入：[N, m^l, hidden_channel]，实现时（看作是node_batch_size * sequence_len * embedding_size），注意这里的batch_size不是图的batch_size，而是节点的batch_size，是个固定值，即node_batch_size=N
  • 输出：[N, m^(l+1), hidden_channel]，实现时（看作是node_batch_size * sequence_len * embedding_size）

  batch-normalization层（每两个时间block后）：

  • 输入：[N, m^l, c^l]
  • 输出：[N, m^l, c^l]

  FC层：

  • 输入：[N, m^l, c^l]
  • 输出：[N, F]

  第l层空间block：

  • GCN层：

  输入：[graph_batch_size, n^l，input_feature], n^l为当前层图中节点数量
  输出：[graph_batch_size, n^l，hidden_channel1]

  • pooling层

  注意这是论文改进的地方，提出了一种新方法，将图转化为一个规模更小的子图。

  • 输入：[graph_batch_size, n^l，hidden_channel]
  • 输出：[graph_batch_size, n^(l+1)，hidden_channel1]

  • 权重矩阵更新：

  • 输入权重矩阵：[n^(l+1),n^(l+1)]
  • 输出权重矩阵：[n^(l+1),n^(l+1)]

  合并层：
  注意，这里首先是对每个空间block的输出进行均值池化和max池化，然后concat起来。接着将所有空间block池化后的结果进行加和。

  • 输入：[graph_batch_size, n^l，hidden_channel1]
  • 输出：[graph_batch_size，2*hidden_channel1]

  输出层：

  • 输入：[graph_batch_size，2*hidden_channel1]
  • 输出：[graph_batch_size，num_classes]

  最后进行一个softmax即可。损失函数使用交叉熵损失。

  • 模型参数

  • $N=768$
  • $F=60$
  • $M=1000$
  • $n^{(l+1)}=60\%\ast n^l$
  • $epoch=100$，当验证损失开始上升时，提前结束
  • $graph\_batch\_size=25$
  • $learnin{g}_{r}ate=0.001$，$decay\_rate=0.7$
  • 优化器：Adam
  • $hidden\_channel=8，stride=1$
  • $hidden\_channel1=60$

4. 模型评估

• 实验环境

  所有实验均在Linux机器(CPU: Intel® Core™ i7, GPU: NVIDIA GeForce RTX 2060)上编译和测试。

• 数据集

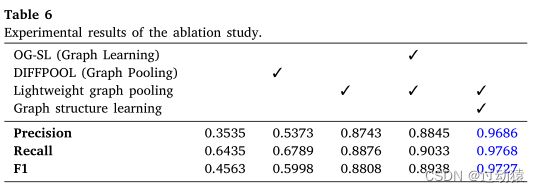
  为了评估我们提出的模型的性能，如图6所示，我们构建了一个网络环境，构造了2个加密的流量数据集。

  • OBW30：该数据集由3万+数千个加密流量流组成，经过数据包重组和流减少技术后，属于30种HTTPS (HTTP over SSL/TLS)流量数据。如表1所示，这些流量数据是由3个操作系统、2个web浏览器和5个流行应用程序生成的。
  • HW19：该数据集包含19,000 + HTTPS流量，参考19个流行的web应用程序，经过数据包重组和流量减少技术。如表2所示，这些应用包括抖音、Bilibili、微博、Github、斗鱼、NeCmusic、百度、iCloud、QQ、豆瓣等。

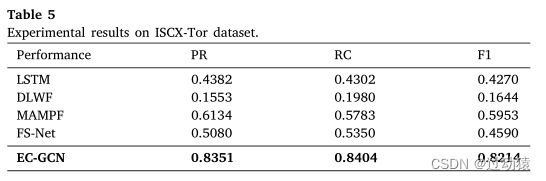
  为了进一步评估Onion 路由器（Tor）下EC-GCN的有效性，我们在一个公开可用的数据集（ISCX-Tor）上进行了实验。

  ISCX-Tor[34]。该数据集由3021个加密流量流和8万个数据包组成，涉及16个应用程序。这类流量通过分布式路由网络在发送端和接收端之间进行模糊通信，对模式提取和分类更具挑战性。该数据集涉及多种加密算法，包括SSL/TLS、SSH等。

• 模型参数

  • $N=768$
  • $F=60$
  • $M=1000$
  • $n^{(l+1)}=60\%\ast n^l$
  • $epoch=100$，当验证损失开始上升时，提前结束
  • $graph\_batch\_size=25$
  • $learnin{g}_{r}ate=0.001$，$decay\_rate=0.7$
  • 优化器：Adam
  • $hidden\_channel=8，stride=1$
  • $hidden\_channel1=60$

• 基线模型

  • LSTM
  • 深度学习网站指纹识别(DLWF)[24]：一种基于DL的通过网络数据包的时间和大小进行网站指纹识别的方法
  • MAMPF[22]：一种使用消息类型和长度块马尔可夫模型的输出概率作为特征对加密流量进行随机森林分类器分类的方法
  • 用于加密流分类的流序列网络(FS-Net)[27]：一个基于Bi-GRU的分类模型，它学习加密流的代表性特征，然后对其进行分类。

• 评估指标

  Precision (PR)， Recall (RC)， F1-score (F1)

• 实验结果
  
  

• 图规模对模型预测时间的影响：
  

• 模型鲁棒性
  

• 消融实验
  

总结

论文内容

1. 学到的方法

   理论上的方法：

   1. 提供了一种构图的新思路：以一个流作为一个图，节点特征为数据包长度，边权重为数据包长度的转移概率。
   2. 为了提高模型的实时性，提出了一种轻量级的图池化层，从而在训练过程中逐层将图转化为一个规模更小的子图。具体实现方法如下：
      $$H^{(l+1)}=S^{(l)}{H}^{(l)}，其中H^{(l+1)}\in R^{n^{l+1}\times F}$$$$W^{(l+1)}=S^{(l)T}{W}^{(l)}{S}^{(l)}，其中W^{(l+1)}\in R^{n^{l+1}\times n^{l+1}}$$
   3. 图中边权重矩阵$W$学习图结构的方法：

   首先定义一个 $IR$
   $$IR=D^{(l)-1}{W}^{(l)}{H}^{(l)}，其中IR\in R^{n^l\times F}$$其中 $D^{(l)}$ 表示 $W^{(l)}$的对角度矩阵
   IR表示图中每个节点的交互得分，如果IR的某一行中的数值越大，就证明该节点（该行）与其余邻居节点交互越频繁。下面具体介绍当前 l 层的权重矩阵如何计算：
   

2. 论文优缺点

   优点：

   1. 考虑了模型的实时性。在构建模型时使用了轻量级的pooling方法，逐层降低图的规模，同时还考虑了边权重矩阵的更新，从而使得降低图规模时造成的信息损失减小。
   2. 只使用了数据包长特征。并根据这一个特征提取了它的时间和空间信息。

   缺点：

   1. 由于只使用元数据特征作为输入，EC-GCN可能会受到一些流量整形操作的影响，例如填充入包以正则化报文长度序列[36]。

   解决思路：可以通过集成更多的元数据特征，包括数据包类型序列、数据包间隔序列和上行/下行序列等，在一定程度上克服这一问题。

   2. 难以应对协议变化和流量混淆的鲁棒算法。
   3. 如果流中数据包很少（短流），那么就无法进行图构建，从而使得模型的效果大打折扣

数据集

• OBW30：自行收集的数据集
• HW19：自行收集的数据集
• ISCX-Tor [34]：公共的数据集