【数据结构:稀疏矩阵的基本操作】

本实验用C语言实现

稀疏矩阵:矩阵阶数很大，非零元个数较少，零元很多，但非零元的排列没有一定规律。

三元组表法:一种顺序存储（按行优先顺序存放）。一个非零元有行号、列号、值，为一个三元组，整个稀疏矩阵中非零元的三元组合起来称为三元组表。

实验内容:
1、设计三元组表的物理存储结构
2、设计稀疏矩阵的建立算法（数据从键盘输入）
如

0   0   0   0   3
0   0   1   2   0
0   5   0   0   0
6   0   0   0   9

3、设计稀疏矩阵的数据输出算法（输出方式以三元组表形式输出，但要求输出相应数据元素的行号、列号、元素数值）
4、设计稀疏矩阵的数据输出算法（输出方式以矩阵形式输出）
5、设计两个稀疏矩阵的加法算法（在main函数中验证输出结果）

===================================================================

头部

#include
#include 
#include 
using namespace std;
//#include

#define maxsize 100    //定义非零元的最大数目
typedef int elemtype;

1.设计三元组表的物理存储结构

//定义一个 三元组
typedef struct{  
	int i, j;    //非零元 行、列号
	elemtype e;  //非零元值
}Triple;
//定义 稀疏矩阵
typedef struct 
{
	int mu, nu;           //稀疏矩阵行、列数
	int tu;              //稀疏矩阵非零元个数
	Triple data[maxsize+1];      //三元组表
}TSMatrix;

TSMatrix M; //定义稀疏矩阵M

我定义的稀疏矩阵的存储结构有四个属性,分别是 稀疏矩阵的行数-mu,列数-nu,非零元个数-tu,以及存储其非零元行,列,值的结构体数组-data

2、设计稀疏矩阵的建立算法（数据从键盘输入）

//初始化 稀疏矩阵
TSMatrix initMatrix(int row,int col,int num){
	TSMatrix M;
	M.mu = row;
	M.nu = col;
	M.tu = num;
	return M;
}

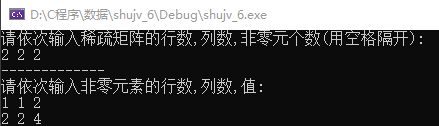
上面的代码块为稀疏矩阵的初始化,在主函数中通过用户输入希望建立的稀疏矩阵行,列,非零元个数,初始化稀疏矩阵。运行图如下(此部分在主函数中,见博客最后

//稀疏矩阵的建立
TSMatrix inputMatrix(TSMatrix M){
	printf("-------------\n");
	printf("请依次输入非零元素的行数,列数,值:\n");
	for (int i = 1; i <= M.tu; i++) {
		cin >> M.data[i].i >> M.data[i].j >> M.data[i].e;//输入
		getchar();
	}
	return M;
}

用户依次输入非零元素的行数,列数,值,运行图如下

3、设计稀疏矩阵的数据输出算法（输出方式以三元组表形式输出，但要求输出相应数据元素的行号、列号、元素数值）

//遍历输出稀疏矩阵  三元组形式
void traverseMatrix1(TSMatrix M) {
	printf("-------------三元组形式形式遍历输出:\n");
	for (int i = 1; i <= M.mu; i++) {
		cout << M.data[i].i << "行 " << M.data[i].j << "列 " << M.data[i].e << endl;
	}
}

此处用到c++里的输出语句count,循环稀疏矩阵,共M.mu次,运行结果如下

4、设计稀疏矩阵的数据输出算法（输出方式以矩阵形式输出）

//遍历输出稀疏矩阵  矩阵形式
void traverseMatrix2(TSMatrix M) {
	int index = 1;
	printf("-------------矩阵形式遍历输出:\n"); 
	for (int i = 1; i <= M.mu; i++) {
		for (int j = 1; j <=M.nu; j++) {
			if (M.data[index].i==i&& M.data[index].j == j) {
				printf(" %d", M.data[index].e);
				index++;
			}
			else {
				printf(" 0");
			}
		}
		printf("\n");
	}
}

以矩阵形式遍历输出稀疏矩阵,首先就要用 双层for循环 遍历矩阵的每行每列的每个元素,再判断在这个位置是否是非零元素,如果是,就输出非零元素的值,如果不是,就输出零,运行结果如下

5、设计两个稀疏矩阵的加法算法（在main函数中验证输出结果）

矩阵的加法算法函数如下,首先定义一系列将会用到的变量

//矩阵的加法
TSMatrix addMatrix(int row, int col) {
	TSMatrix W; //第二个稀疏矩阵
	TSMatrix WM;//矩阵的和
	W.mu = row;
	W.nu = col;
	WM.mu = row;
	WM.nu = col;
	int indexW = 1;
	int indexM = 1;
	int indexWM = 1;
	int a, b;//两个加数
	int sum;//和
	printf("-------------\n");

接下来,在定义用于加法的第二个稀疏矩阵,并让用户输入第二个矩阵非零元素个数,以及行,列,非零元素的个数,运行图如下

	printf("请输入第二个一个%d行%d列的稀疏矩阵的非零元个数",row,col);
	scanf("%d", &W.tu);
	printf("请依次输入非零元素的行数,列数,值:\n");
	//输入
	for (int i = 1; i <= W.tu; i++) {
		cin >> W.data[i].i >> W.data[i].j >> W.data[i].e;
		getchar();
	}

然后,我们可以写两个遍历算法,检查一下刚刚输入的稀疏矩阵是否成功赋值,也可以顺带遍历之前第一个稀疏矩阵是否正确,运行结果如下

//矩阵形式遍历
	printf("第一个矩阵为:\n");
	for (int i = 1; i <= M.mu; i++) {
		for (int j = 1; j <= M.nu; j++) {
			if (M.data[indexM].i == i && M.data[indexM].j == j) {
				printf(" %d", M.data[indexM].e);
				indexM++;
			}
			else {
				printf(" 0");
			}
		}
		printf("\n");
	}
	printf("第二个矩阵为:\n");
	for (int i = 1; i <= W.mu; i++) {
		for (int j = 1; j <= W.nu; j++) {
			if (W.data[indexW].i == i && W.data[indexW].j == j) {
				printf(" %d", W.data[indexW].e);
				indexW++;
			}
			else {
				printf(" 0");
			}
		}
		printf("\n");
	}

接下来,到了将两个矩阵进行加法运算的阶段了,因为本实验定义两个相加的矩阵同行同列,故其相加所得和矩阵WM也与两个加数同行同列。
故,循环遍历和矩阵i行j列的元素,再检查这个位置上W矩阵和M矩阵是否有值(没有值则为零),相加得这个位置上WM和矩阵的值,最后遍历出来即可,遍历结果如下。

//加法
	indexW = 1;
	indexM = 1;
	for (int i = 1; i <= WM.mu; i++) {
		for (int j = 1; j <= WM.nu; j++) {
			a = 0;
			b = 0;
			if ((M.data[indexM].i == i)&&(M.data[indexM].j == j)) {
				a = M.data[indexM].e;
				indexM++;
			}
			if ((W.data[indexW].i == i)&&(W.data[indexW].j == j)) {
				b = W.data[indexW].e;
				indexW++;
			}
			sum = a + b;
			getchar();
			if (sum != 0) {
				WM.data[indexWM].e = sum;
				WM.data[indexWM].i = i;
				WM.data[indexWM].j = j;
				indexWM++;
			}
		}
		printf("\n");
	}
	indexWM = 1;
	printf("矩阵之和为:\n");
	for (int i = 1; i <= WM.mu; i++) {
		for (int j = 1; j <= WM.nu; j++) {
			if (WM.data[indexWM].i == i && WM.data[indexWM].j == j) {
				printf(" %d", WM.data[indexWM].e);
				indexWM++;
			}
			else {
				printf(" 0");
			}
		}
		printf("\n");
	}
	return M;
}

主函数代码如下

//主函数
int main() {
	int row, col, num;
	//用户输入行列数
	printf("请依次输入稀疏矩阵的行数,列数,非零元个数(用空格隔开):\n");
	scanf("%d %d %d", &row, &col, &num);
	//初始化稀疏矩阵
	M = initMatrix(row, col, num);
	//输入
	M = inputMatrix(M);
	//遍历输出
	traverseMatrix1(M);
	traverseMatrix2(M);
	//矩阵的加法
	addMatrix(row, col);
	getchar();
	getchar();
	getchar();
}