代码随想录第19天 | 235. 二叉搜索树的最近公共祖先 701.二叉搜索树中的插入操作 450.删除二叉搜索树中的节点

235. 二叉搜索树的最近公共祖先

var lowestCommonAncestor = function(root, p, q) {
    // 使用递归的方法
    // 1. 使用给定的递归函数lowestCommonAncestor
    // 2. 确定递归终止条件
    if(root === null) {
        return root;
    }
    if(root.val > p.val && root.val > q.val) {
        // 向左子树查询
         return root.left = lowestCommonAncestor(root.left,p,q);
    }
    if(root.val < p.val && root.val < q.val) {
        // 向右子树查询
        return root.right = lowestCommonAncestor(root.right,p,q);
    }
    return root;  //直接返回，无须对中间节点操作
};


*************************************************************************
var lowestCommonAncestor = function(root, p, q) {
    // 使用迭代的方法
    while(root) {
        if(root.val > p.val && root.val > q.val) {
            root = root.left;
        }else if(root.val < p.val && root.val < q.val) {
            root = root.right;
        }else {
            return root;
        }
        
    }
    return null;
};

第一想法

没有想法

思路

• 二分法

第一次遇到 cur节点是数值在[p, q]区间中，那么cur就是 p和q的最近公共祖先。

理解这一点，本题就很好解了。

而递归遍历顺序，本题就不涉及到 前中后序了（这里没有中节点的处理逻辑，遍历顺序无所谓了）。

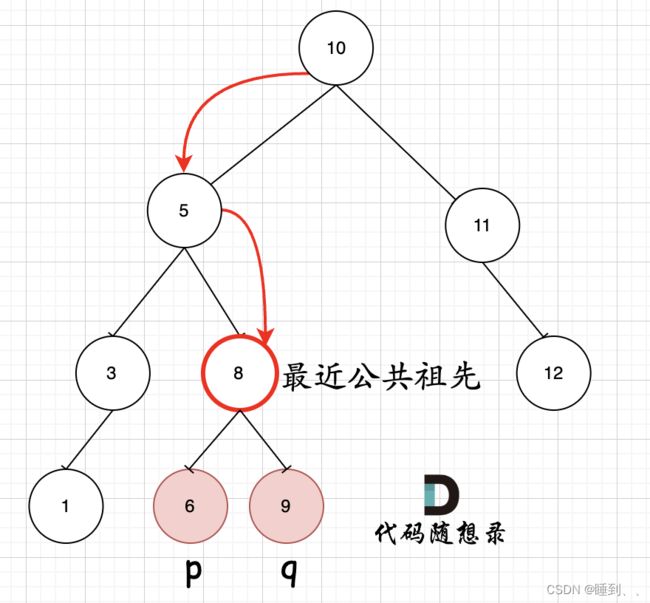
如图所示：p为节点6，q为节点9

可以看出直接按照指定的方向，就可以找到节点8，为最近公共祖先，而且不需要遍历整棵树，找到结果直接返回！

---

701.二叉搜索树中的插入操作

       var insertIntoBST = function (root, val) {
           if (root === null) {
               return root = new TreeNode(val, null, null);
           }
           var b = function (root, val) {
               if (root === null) {
                   return root;
               }
               if (root.val > val) {
                   // 向左子树查询
                   if (!root.left) root.left = new TreeNode(val, null, null)
                   root.left = insertIntoBST(root.left, val);
               }
               if (root.val < val) {
                   // 向右子树查询
                   if (!root.right)
                       root.right = new TreeNode(val, null, null)
                   root.right = insertIntoBST(root.right, val);
               }
               return root
           };
           return b(root, val)
       }
*****************************************************************************
//卡哥的递归做法
var insertIntoBST = function (root, val) {
    const setInOrder = (root, val) => {
        if (root === null) {
            let node = new TreeNode(val);
            return node;
        }
        if (root.val > val)
            root.left = setInOrder(root.left, val);
        else if (root.val < val)
            root.right = setInOrder(root.right, val);
        return root;
    }
    return setInOrder(root, val);
};

第一想法

二分+递归（迭代也行）

思想

只要按照二叉搜索树的规则去遍历，遇到空节点就插入节点就可以了。

例如插入元素10 ，需要找到末尾节点插入便可，一样的道理来插入元素15，插入元素0，插入元素6，需要调整二叉树的结构么？ 并不需要。。

只要遍历二叉搜索树，找到空节点 插入元素就可以了，那么这道题其实就简单了

我的做法

• 结束判断，在b函数前加一个[]情况

• 其实他的路线也只遍历了一条，然后返回他的root

卡哥的

差不多，不过他在 if (root === null) 这里添加节点，省去了在比较时候的判断，包括我开头一步的判断[]

450.删除二叉搜索树中的节点

第一想法

先迭代（二分法）找到这个节点，然后继续迭代(全部)，加入上一道题的函数。写不出来

思想

思路一

var deleteNode = function(root, key) {
    if (!root) return null;
    if (key > root.val) {
        root.right = deleteNode(root.right, key); //向右递归
        return root;  //一定是返回自己
    } else if (key < root.val) {
        root.left = deleteNode(root.left, key); //向左递归
        return root;
    } else { //相等的情况
        // 场景1: 该节点是叶节点
        if (!root.left && !root.right) {
            return null   //往上返回一级就是root.left = null
        }
        // 场景2: 有一个孩子节点不存在
        if (root.left && !root.right) {
            return root.left;  //直接就是返回它的一半
        } else if (root.right && !root.left) {
            return root.right;
        }
        // 场景3: 左右节点都存在
        const rightNode = root.right;  //记录它的右节点的最左叶子
        // 获取最小值节点
        const minNode = getMinNode(rightNode);  //左遍历
      //最右边最小值加上左子树（root的left）
        minNode.left=root.left
     //返回root的右边
        return root.right;
    }
};
function getMinNode(root) {
    while (root.left) {
        root = root.left;
    }
    return root;
}

思路二（最后一步改了哈，使之高度没那么高）：

var deleteNode = function(root, key) {
    if (!root) return null;
    if (key > root.val) {
        root.right = deleteNode(root.right, key); //向右递归
        return root;  //一定是返回自己
    } else if (key < root.val) {
        root.left = deleteNode(root.left, key); //向左递归
        return root;
    } else { //相等的情况
        // 场景1: 该节点是叶节点
        if (!root.left && !root.right) {
            return null   //往上返回一级就是root.left = null
        }
        // 场景2: 有一个孩子节点不存在
        if (root.left && !root.right) {
            return root.left;  //直接就是返回它的一半
        } else if (root.right && !root.left) {
            return root.right;
        }
        // 场景3: 左右节点都存在
        const rightNode = root.right;  //记录它的右节点的最左叶子
        // 获取最小值节点
        const minNode = getMinNode(rightNode);  //左遍历
        // 将待删除节点的值替换为最小值节点值
        root.val = minNode.val;  //7换成8?
        // 删除最小值节点
        root.right = deleteNode(root.right, minNode.val); //懂了
        return root;
    }
};
function getMinNode(root) {
    while (root.left) {
        root = root.left;
    }
    return root;
}

困难

• 看不懂普通的二叉树删除

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == nullptr) return root;
        if (root->val == key) {
            if (root->right == nullptr) { // 这里第二次操作目标值：最终删除的作用
                return root->left;
            }
            TreeNode *cur = root->right;
            while (cur->left) {
                cur = cur->left;
            }
            swap(root->val, cur->val); // 这里第一次操作目标值：交换目标值其右子树最左面节点。
        }
        root->left = deleteNode(root->left, key);
        root->right = deleteNode(root->right, key);
        return root;
    }
};

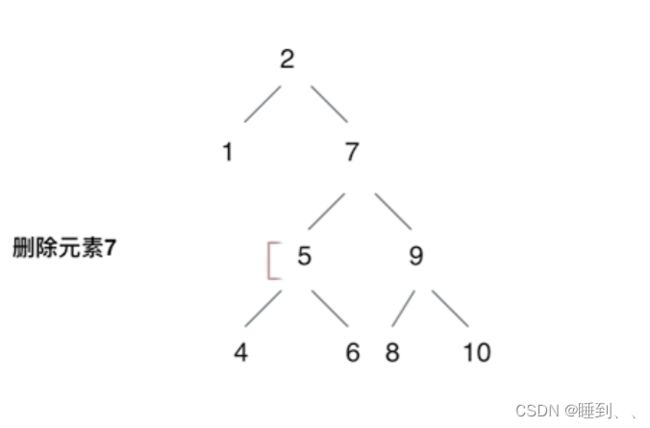
普通二叉树的删除方式（没有使用搜索树的特性，遍历整棵树），用交换值的操作来删除目标节点。
代码中目标节点（要删除的节点）被操作了两次：

• 第一次是和目标节点的右子树最左面节点交换。
• 第二次直接被NULL覆盖了