基于数据驱动的智能空调系统需求响应可控潜力评估研究（Matlab代码实现）

欢迎来到本博客 ❤️ ❤️


博主优势： 博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。


⛳ 座右铭：行百里者，半于九十。

本文目录如下：
目录
1 概述
2 运行结果
3 参考文献
4 Matlab代码、数据、文章讲解

1 概述

文献来源：

摘要：住宅空调负荷（ACL）是一种有前途的需求响应（DR）资源，具有一定的灵活性和可控性，可以提高电网的运行灵活性和资源利用率。灾难恢复潜力评估对于估计功率降低和确定合适的灾难恢复客户非常重要。为了更好地揭示灾难恢复过程中的多方面因素和多重不确定性，本文提出了一种新的定义和评估方法，用于从单个客户到大规模地区的运营灾难恢复潜力。为了解决两个主要的评估问题：ACLs提取和参数估计，提出了一种考虑负荷水平差异和季节变化的无监督负荷分解方法，将全屋能耗分解为ACLs和基本负荷分量，随后，基于ACL的热动力学模型，开发了用于静态和动态模型参数估计的分段分析方法。对所提出的方法进行了深入的实施，以分析ACL的消费行为，并针对不同时间尺度的DR计划以经济高效的方式瞄准客户。

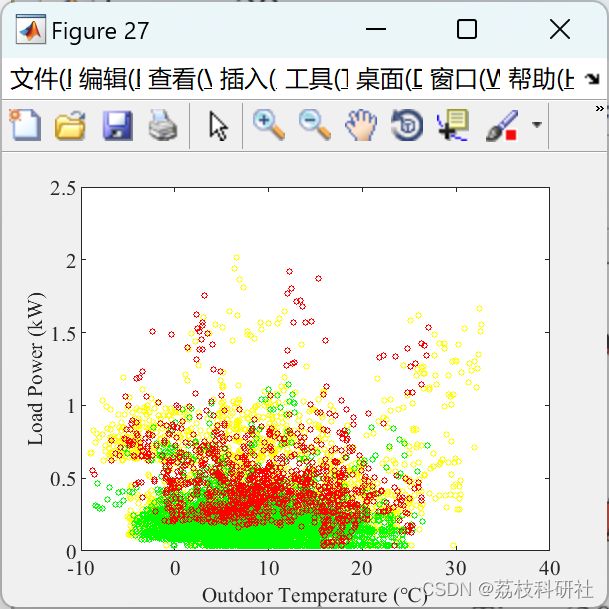
本文首先评估单一客户的空调可控潜力，进而发展为大规模地区的空调的需求响应潜力以及规模的评估。采用静态和动态模型参数估计的分段分析方法，深入分析了空调负荷的消费行为，并针对不同时间尺度的需求响应问题，以成本效益为目标，优化空调负荷的需求响应行为。最后以实际的算例数据，验证了所提出方法的准确性和鲁棒性。文献基于德克萨斯州奥斯汀市119个居民客户的地面真实数据进行的数据实验验证了所提出的方法具有更好的准确性和鲁棒性。这些结果还表明，ACL使用模式（共19种模式）和灾难恢复潜力（最大3.2 kW）的巨大差异来自不同的灾难恢复持续时间和运营条件，这表明政策和计划应参考不同灾难恢复场景中灾难恢复客户目标和参与者选择的5个基本指标。

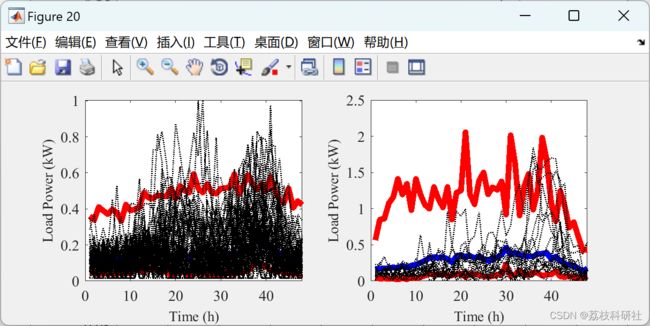
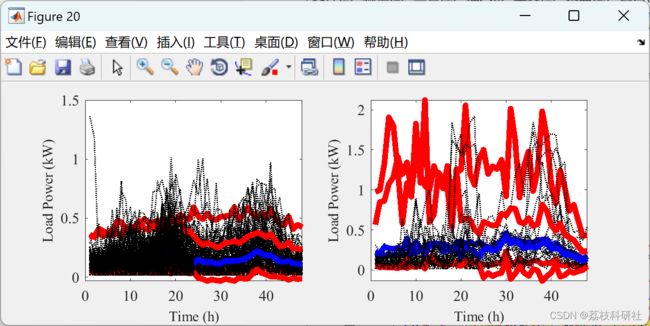
2 运行结果

部分代码：

figure(7)

set(gcf,'unit','centimeters','position',[0,0,16,12])

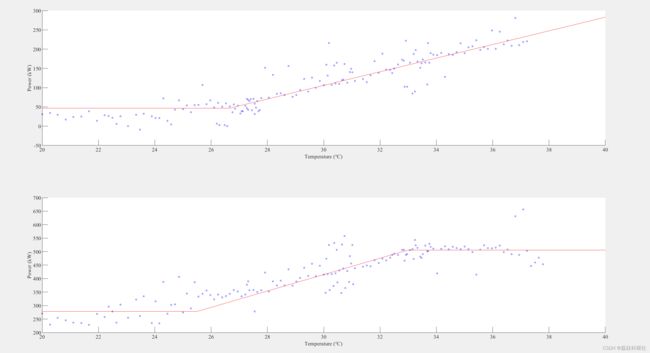
plot([temp3weekday;temp3weekend],[P3baseloadweekday;P3baseloadweekend],'o','MarkerSize',2);

set(gca,'FontName','Times New Roman','FontSize',10.5)

xlabel('\fontsize{10.5}\fontname{Times new roman}Outdoor Temperature (℉)')

ylabel('\fontsize{10.5}\fontname{Times new roman}Load Power (kW)')

figure(8)

set(gcf,'unit','centimeters','position',[0,0,16,12])

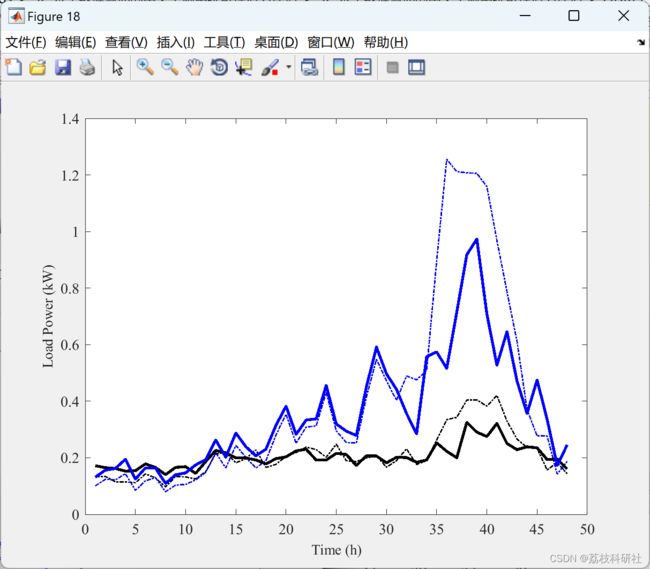
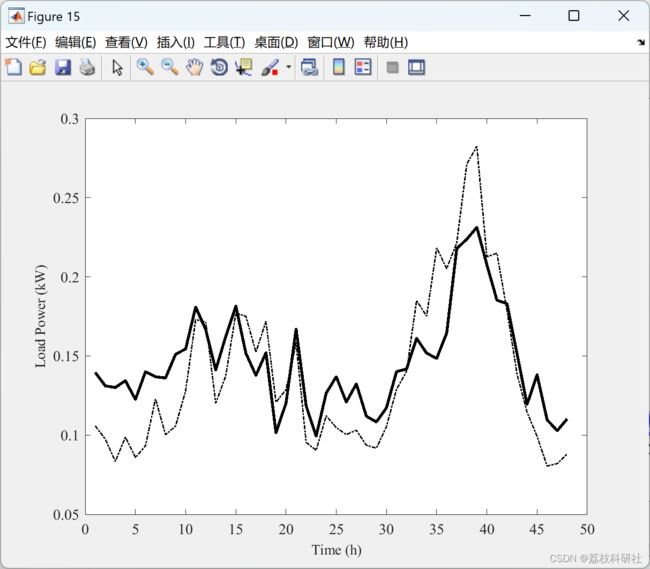
plot(mean(P3baseloadweekdaytrue),'k-.','LineWidth',1)

hold on

plot(mean(P3baseloadweekendtrue),'b-.','LineWidth',1)

hold on

plot(mean(P3baseloadweekday),'k-','LineWidth',2)

hold on

plot(mean(P3baseloadweekend),'b-','LineWidth',2)

hold on

set(gca,'FontName','Times New Roman','FontSize',10.5)

xlabel('\fontsize{10.5}\fontname{Times new roman}Time (h)')

ylabel('\fontsize{10.5}\fontname{Times new roman}Load Power (kW)')

%% clustering of April

Pcluster=P4;

temp4=T4;

[idx,C,sumD]=kmeans(Pcluster,4);

[Y,I]=sort(mean(C'));

P4baseloadweekday=Pcluster(find(idx==I(1)),:);

P4baseloadweekend=Pcluster(find(idx==I(3)),:);

P4otherweekday=Pcluster(find(idx==I(2)),:);

P4otherweekend=Pcluster(find(idx==I(4)),:);

cluster4=zeros(size(idx,1),1);

cluster4(find(idx==I(1)),1)=1;

cluster4(find(idx==I(3)),1)=2;

cluster_4=zeros(size(idx,1),1);

cluster_4([find(idx==I(1));find(idx==I(3))],1)=1;

P4baseloadweekdaytrue=baseload4(find(idx==I(1)),:);

P4baseloadweekendtrue=baseload4(find(idx==I(4)),:);

weekday4=[find(idx==I(1));find(idx==I(2))];

weekend4=[find(idx==I(3));find(idx==I(3))];

temp4weekday=temp4(find(idx==I(1)),:);

temp4weekend=temp4(find(idx==I(3)),:);

temp4otherweekday=temp4(find(idx==I(2)),:);

temp4otherweekend=temp4(find(idx==I(4)),:);

figure(7)

set(gcf,'unit','centimeters','position',[0,0,16,12])

plot([temp3weekday;temp3weekend],[P3baseloadweekday;P3baseloadweekend],'o','MarkerSize',2);

set(gca,'FontName','Times New Roman','FontSize',10.5)

xlabel('\fontsize{10.5}\fontname{Times new roman}Outdoor Temperature (℉)')

ylabel('\fontsize{10.5}\fontname{Times new roman}Load Power (kW)')

%% weekday correction

3 参考文献

部分理论来源于网络，如有侵权请联系删除。

4 Matlab代码、数据、文章讲解