探索实践低光照场景下YOLOv5s模型上限，融合CBAM注意力机制开发构建基于改进YOLOv5s的低光照条件下目标检测识别分析系统

在现实生活场景里面，很多场景下光线光照条件都是比较差的，比如夜晚、室内等，这时候以往的目标检测模型是否还能够胜任我们所需的目标检测任务呢？这里主要的想法就是基于地光线条件下的数据集来开发构建目标检测系统，探索分析传统轻量级的检测模型在这样场景下是否还具备竞争力。

首先看下效果图：

简单看下数据集，数据集来源于网络源：

 可以看到：整体数据的光线光照条件都是很一般的。

标注文件如下所示：

 实例标注内容如下：

4 0.344675 0.89645 0.204142 0.100592
11 0.702663 0.885602 0.156805 0.094675
7 0.840237 0.894477 0.189349 0.100592
6 0.230769 0.822485 0.053254 0.031558
8 0.482249 0.861933 0.100592 0.051282
0 0.428994 0.844181 0.065089 0.043393

 这里主要的基准模型是yolov5s，如下：

# Parameters
nc: 12
depth_multiple: 0.33
width_multiple: 0.50


anchors:
  - [10,13, 16,30, 33,23]
  - [30,61, 62,45, 59,119] 
  - [116,90, 156,198, 373,326]



backbone:
  # [from, number, module, args]
  [[-1, 1, Conv, [64, 6, 2, 2]],  # 0-P1/2
   [-1, 1, Conv, [128, 3, 2]],    # 1-P2/4
   [-1, 3, C3, [128]],
   [-1, 1, Conv, [256, 3, 2]],    # 3-P3/8
   [-1, 6, C3, [256]],
   [-1, 1, Conv, [512, 3, 2]],    # 5-P4/16
   [-1, 9, C3, [512]],
   [-1, 1, Conv, [1024, 3, 2]],   # 7-P5/32
   [-1, 3, C3, [1024]],
   [-1, 1, SPPF, [1024, 5]],      # 9
  ]



head:
  [[-1, 1, Conv, [512, 1, 1]],
   [-1, 1, nn.Upsample, [None, 2, 'nearest']],
   [[-1, 6], 1, Concat, [1]],  # cat backbone P4
   [-1, 3, C3, [512, False]],  # 13

   [-1, 1, Conv, [256, 1, 1]],
   [-1, 1, nn.Upsample, [None, 2, 'nearest']],
   [[-1, 4], 1, Concat, [1]],  # cat backbone P3
   [-1, 3, C3, [256, False]],  # 17 (P3/8-small)

   [-1, 1, Conv, [256, 3, 2]],
   [[-1, 14], 1, Concat, [1]],  # cat head P4
   [-1, 3, C3, [512, False]],  # 20 (P4/16-medium)

   [-1, 1, Conv, [512, 3, 2]],
   [[-1, 10], 1, Concat, [1]],  # cat head P5
   [-1, 3, C3, [1024, False]],  # 23 (P5/32-large)

   [[17, 20, 23], 1, Detect, [nc, anchors]],  # Detect(P3, P4, P5)
  ]

加入CBAM注意力机制的改进模型如下：

# YOLOv5  by Ultralytics, GPL-3.0 license

# Parameters
nc: 12  # number of classes
depth_multiple: 0.33  # model depth multiple
width_multiple: 0.50  # layer channel multiple
anchors:
  - [10,13, 16,30, 33,23]  # P3/8
  - [30,61, 62,45, 59,119]  # P4/16
  - [116,90, 156,198, 373,326]  # P5/32



#Backbone
backbone:
  # [from, number, module, args]
  [[-1, 1, Conv, [64, 6, 2, 2]],  # 0-P1/2
   [-1, 1, Conv, [128, 3, 2]],  # 1-P2/4
   [-1, 3, C3, [128]],
   [-1, 1, Conv, [256, 3, 2]],  # 3-P3/8
   [-1, 6, C3, [256]],
   [-1, 1, Conv, [512, 3, 2]],  # 5-P4/16
   [-1, 9, C3, [512]],
   [-1, 1, Conv, [1024, 3, 2]],  # 7-P5/32
   [-1, 3, C3, [1024]],
   [-1, 1, SPPF, [1024, 5]],  # 9
  ]



#Head
head:
  [[-1, 1, Conv, [512, 1, 1]],
   [-1, 1, nn.Upsample, [None, 2, 'nearest']],
   [[-1, 6], 1, Concat, [1]],  # cat backbone P4
   [-1, 3, C3, [512, False]],  # 13

   [-1, 1, Conv, [256, 1, 1]],
   [-1, 1, nn.Upsample, [None, 2, 'nearest']],
   [[-1, 4], 1, Concat, [1]],  # cat backbone P3
   [-1, 3, C3, [256, False]],  # 17 (P3/8-small)

   [-1, 1, Conv, [256, 3, 2]],
   [[-1, 14], 1, Concat, [1]],  # cat head P4
   [-1, 3, C3, [512, False]],  # 20 (P4/16-medium)

   [-1, 1, Conv, [512, 3, 2]],
   [[-1, 10], 1, Concat, [1]],  # cat head P5
   [-1, 3, C3, [1024, False]],  # 23 (P5/32-large)
   [-1, 1, CBAM, [1024]], 

   [[17, 20, 24], 1, Detect, [nc, anchors]],  # Detect(P3, P4, P5)
  ]

默认都是100次epoch的迭代计算，看下模型对比结果。

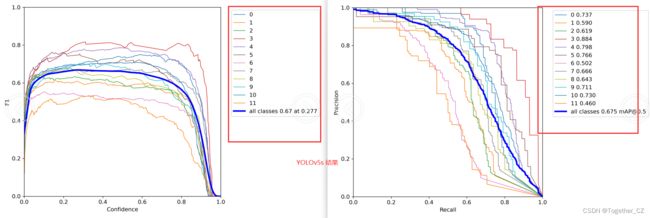
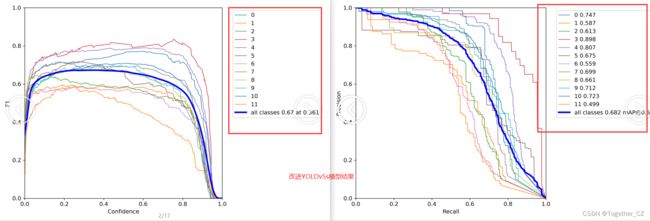
原生YOLOv5s模型结果如下：

 

改进后的YOLOv5s模型结果如下：

这里着重对比的就是模型的F1和PR曲线，这是能够比较全面综合体现模型性能指标的，但是不够直观不够立体，这里绘制对比曲线来进行详细对比。

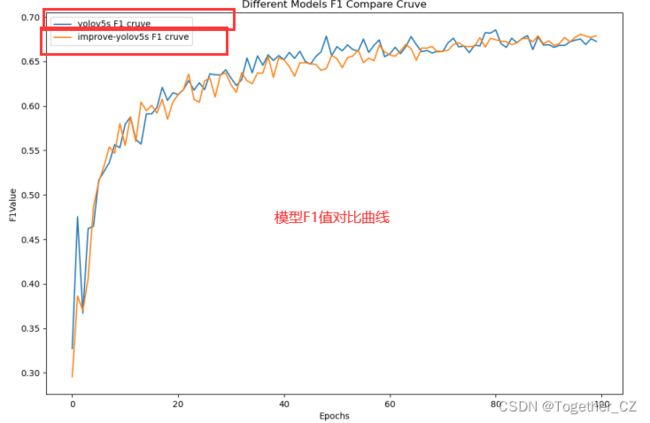
首先是模型的F1值对比曲线，如下：

 可以看到：最初的时候改进模型略占下风，之后和原生模型部分伯仲，最终超出原生模型。

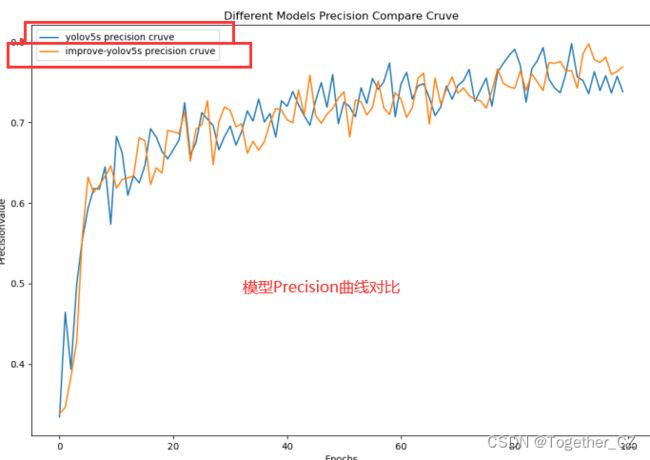
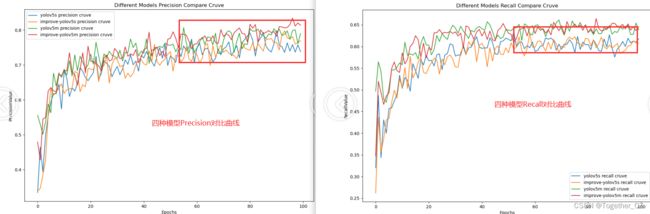
接下来是精确率曲线：

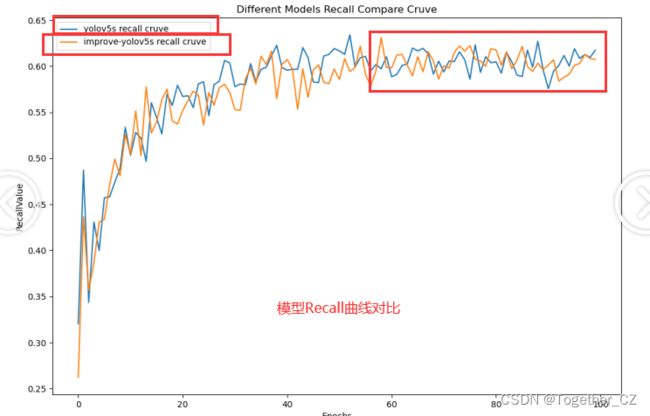
 接下来是召回率对比曲线：

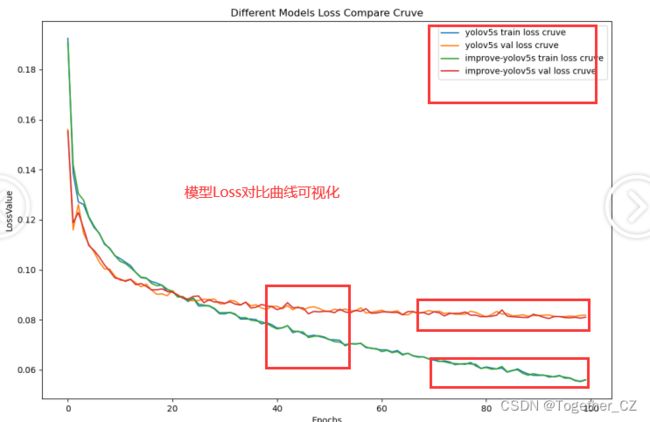
最后我们还对比分析了两款模型整体训练-验证loss曲线，如下：

 整体呈现出来的规律都是接近或者是相似的。

轻量级的YOLOv5s表现出来的性能已经是相对可以的了。

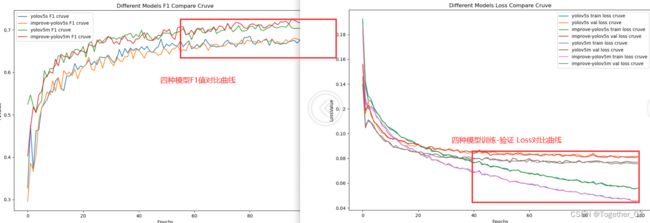
这里突然想到，m系列的模型是否会更好呢，这里我也同样做了原始YOLOv5m和改进版YOLOv5m的模型，整体的构建原理与YOLOv5s是一致的，这里就不再赘述了，直接看下最终的对比结果好了。

 从图表数据呈现出来的结果来看：m系列的模型要更胜一筹，不过本身m的参数量级就更大，结果好也是预料之中的事情，感兴趣的话可以继续坐下l系列和x系列的模型，相信结果会更好的。