C++语法(17)---- 二叉搜索树
1.概念
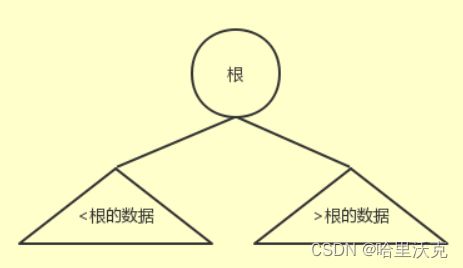
1.父节点的左子树全小于本身
2.父节点的右子树全大于本身
3.左右子树也是二叉搜索树
时间复杂度:O(N),有可能只有左数,这样就遍历了所有,所有复杂度为N
平衡二叉树的时间复杂度才是:O(logN)
2.模拟
1.数据元素设计
1.一个空间存储数据date
2.两个指针,用于指向左右子树的位置
templatestruct BSTreeNode { BSTreeNode(const K& key) :_key(key) ,_left(nullptr) ,_right(nullptr) {} BSTreeNode * _left; BSTreeNode * _right; K _key; };
2. 搜索二叉树类的定义
template
class BSTree
{
private:
Node* _root = nullptr;
};
3.构造函数,拷贝构造,赋值拷贝
1.构造函数,直接定义空树
2.拷贝构造,取调用私有的copy函数
3.赋值拷贝,直接swap两个地址
copy函数的实现,其实是递归拷贝
1.确认传入参数是二叉搜索树的指针;返回返回头指针
2.如果指向的指针是空,则返回
3.构造函数后再考虑左右,所以实现是靠前序遍历
4.一个节点为单位,指向有数据的节点,则new一个新的指针,数据拷贝
5.new出来的子节点,左树由copy函数构建,右树也由copy函数构建
BSTree()
:_root(nullptr)
{}
BSTree(const BSTree& t)
{
_root = Copy(t._root);
}
BSTree& operator=(BSTree t)
{
swap(_root, t._root);
return *this;
}
private:
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newroot = new Node(root->_key);
newroot->_left = Copy(root->_left);
newroot->_right = Copy(root->_right);
return newroot;
} 4.析构函数
析构函数,调用Destory函数,再把_root指向空
相同的,Destory也可以通过递归销毁
1.确认传入参数是二叉搜索树的指针;由于销毁所以返回的值不需要
2.如果指向的指针是空,则返回
3.前面的销毁,后面就找不到了;所以我们要到最后再销毁最开始的指针,所以用后后续遍历
4.Destory左右子树
5.走到最后,要销毁指针
~BSTree()
{
Destory(_root);
_root = nullptr;
}
private:
void Destory(Node* root)
{
if (root == nullptr)
return;
Destory(root->_left);
Destory(root->_right);
delete root;
}5.二分法实现增删查
由于左小右大,完美符合二分法的实现
Insert
1.如果为空,则更新_root,把节点的数据存储k;如果不为空向下走
2.临时变量cur和parent指针,cur指向开头;随后比较,小左大右;更新parent为旧的cur
3.如果夹在中间的k跟parent与cur存在逻辑矛盾返回false
4.k夹在parent和cur之间,cur位置就是k要存储的位置;cur重新new成数据为k的节点,通过parent指针找到原先的cur,中间插入即可,随后返回true
Find:直接找,二分法,找到了返回true,找不到返回false
Erase:先找到该k数据对于节点,随后请看代码的注释
bool Insert(const K& k)
{
if (_root == nullptr)
{
_root = new Node(k);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < k)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > k)
{
parent = cur;
cur = cur->_left;
}
else
return false;
}
cur = new Node(k);
if (parent->_key > k)
parent->_left = cur;
else
parent->_right = cur;
return true;
}
bool Find(const K& k)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < k)
cur = cur->_right;
else if (cur->_key > k)
cur = cur->_left;
else
return true;
}
return false;
}
bool Erase(const K& k)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < k)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > k)
{
parent = cur;
cur = cur->_left;
}
else
{
//删除节点的左子树为空
//父节点连接节点的右字数
if (cur->_left == nullptr)
{
if (cur == _root) // 删除的1,2两种情况下,解决parent为空的情况
_root = cur->_right;
else
{
if (parent->_key > k) //说明cur在parent的左边
parent->_left = cur->_right;
else
parent->_right = cur->_right;
}
delete cur;
return true;
}
//删除节点的右子树为空
//父节点连接节点的左字数
else if (cur->_right == nullptr)
{
if (cur == _root)
_root = cur->_left;
else
{
if (parent->_key > k) //说明cur在parent的左边
parent->_left = cur->_left;
else
parent->_right = cur->_left;
}
delete cur;
return true;
}
else
{
Node* pur = cur;
Node* tmp = Get_Max(cur->_left, pur);
cur->_key = tmp->_key;
if (pur->_right == tmp)
pur->_right = tmp->_left;
else
pur->_left = tmp->_right;
delete tmp;
return true;
}
}
}
return false;
}6.递归实现增删查
bool _InsertR(Node*& root, const K& k)
{
if (root==nullptr)
{
root = new Node(k);
return true;
}
if (root->_key < k)
return _InsertR(root->_right, k);
else if (root->_key > k)
return _InsertR(root->_left, k);
else
return false;
}
bool _Find(Node* root, const K& k)
{
if (root == nullptr)
return false;
if (root->_key > k)
_Find(root->_left, k);
else if (root->_key < k)
_Find(root->_left, k);
else
return true;
}
bool _Erase(Node*& root, const K& k)
{
if (root == nullptr)
return false;
if (root->_key > k)
_Erase(root->_left, k);
else if (root->_key < k)
_Erase(root->_right, k);
else
{
Node* del = root;
if (root->_left == nullptr)
root = root->_right;
else if(root->_right == nullptr)
root = root->_left;
else
{
Node* minRight = root->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
swap(root->_key, minRight->_key);
return _Erase(root->_right, k);
}
delete del;
return true;
}
}3.整体实现
template
struct BSTreeNode
{
BSTreeNode(const K& key)
:_key(key)
,_left(nullptr)
,_right(nullptr)
{}
BSTreeNode* _left;
BSTreeNode* _right;
K _key;
};
template
class BSTree
{
typedef BSTreeNode Node;
public:
BSTree()
:_root(nullptr)
{}
BSTree(const BSTree& t)
{
_root = Copy(t._root);
}
BSTree& operator=(BSTree t)
{
swap(_root, t._root);
return *this;
}
~BSTree()
{
Destory(_root);
_root = nullptr;
}
bool Insert(const K& k)
{
if (_root == nullptr)
{
_root = new Node(k);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < k)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > k)
{
parent = cur;
cur = cur->_left;
}
else
return false;
}
cur = new Node(k);
if (parent->_key > k)
parent->_left = cur;
else
parent->_right = cur;
return true;
}
bool Find(const K& k)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < k)
cur = cur->_right;
else if (cur->_key > k)
cur = cur->_left;
else
return true;
}
return false;
}
bool Erase(const K& k)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < k)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > k)
{
parent = cur;
cur = cur->_left;
}
else
{
//删除节点的左子树为空
//父节点连接节点的右字数
if (cur->_left == nullptr)
{
if (cur == _root) // 删除的1,2两种情况下,解决parent为空的情况
_root = cur->_right;
else
{
if (parent->_key > k) //说明cur在parent的左边
parent->_left = cur->_right;
else
parent->_right = cur->_right;
}
delete cur;
return true;
}
//删除节点的右子树为空
//父节点连接节点的左字数
else if (cur->_right == nullptr)
{
if (cur == _root)
_root = cur->_left;
else
{
if (parent->_key > k) //说明cur在parent的左边
parent->_left = cur->_left;
else
parent->_right = cur->_left;
}
delete cur;
return true;
}
else
{
Node* pur = cur;
Node* tmp = Get_Max(cur->_left, pur);
cur->_key = tmp->_key;
if (pur->_right == tmp)
pur->_right = tmp->_left;
else
pur->_left = tmp->_right;
delete tmp;
return true;
}
}
}
return false;
}
void Print()
{
_Print(_root);
cout << endl;
}
/*bool InsertR(const K& k)
{
if (_root == nullptr)
{
_root = new Node(k);
return true;
}
Node* parent = nullptr;
return _InsertR(_root, k, parent);
}*/
bool InsertR(const K& k)
{
return _InsertR(_root, k);
}
bool FindR(const K& k)
{
return _Find(_root, k);
}
bool EraseR(const K& k)
{
return _Erase(_root, k);
}
private:
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newroot = new Node(root->_key);
newroot->_left = Copy(root->_left);
newroot->_right = Copy(root->_right);
return newroot;
}
/*bool _InsertR(Node* root, const K& k, Node* &parent)
{
Node* cur = root;
if (cur != nullptr)
{
if (cur->_key > k)
{
parent = cur;
_InsertR(cur->_left, k, parent);
}
else if (cur->_key < k)
{
parent = cur;
_InsertR(cur->_right, k, parent);
}
}
else
{
cur = new Node(k);
if (parent->_key > k)
parent->_left = cur;
else
parent->_right = cur;
return true;
}
if (root->_key == k)
return false;
}*/
//进阶思路----引用的使用
bool _InsertR(Node*& root, const K& k)
{
if (root==nullptr)
{
root = new Node(k);
return true;
}
if (root->_key < k)
return _InsertR(root->_right, k);
else if (root->_key > k)
return _InsertR(root->_left, k);
else
return false;
}
bool _Find(Node* root, const K& k)
{
if (root == nullptr)
return false;
if (root->_key > k)
_Find(root->_left, k);
else if (root->_key < k)
_Find(root->_left, k);
else
return true;
}
bool _Erase(Node*& root, const K& k)
{
if (root == nullptr)
return false;
if (root->_key > k)
_Erase(root->_left, k);
else if (root->_key < k)
_Erase(root->_right, k);
else
{
Node* del = root;
if (root->_left == nullptr)
root = root->_right;
else if(root->_right == nullptr)
root = root->_left;
else
{
Node* minRight = root->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
swap(root->_key, minRight->_key);
return _Erase(root->_right, k);
}
delete del;
return true;
}
}
void Destory(Node* root)
{
if (root == nullptr)
return;
Destory(root->_left);
Destory(root->_right);
delete root;
}
Node* Get_Max(Node* root, Node* &parent)
{
while (root->_right)
{
parent = root;
root = root->_right;
}
return root;
}
void _Print(Node* root)
{
if (root == nullptr)
return;
_Print(root->_left);
cout << root->_key << " ";
_Print(root->_right);
}
private:
Node* _root = nullptr;
};