数据结构三叉链表与线索二叉树的思路与实现详解

❤️作者主页：微凉秋意
✅作者简介：后端领域优质创作者，CSDN内容合伙人，阿里云专家博主

---

前言

我们知道最常见的链式存储二叉树的结构体中有数据域、左孩子指针以及右孩子指针，通过递归来创建二叉树。显而易见的是，想找到二叉树中任意一个结点的前驱或后继也要通过根结点不断递归，加以辅助变量来完成。这种方法的效率必然不高，因此我们可以采用三叉链表（增加一个父结点）或者增加线索来优化二叉树结构。

注：上面提到的前驱和后继在线索二叉树中实际上是某个顺序的前驱或后继，例如在中序线索二叉树中就叫做中序前驱和中序后继。

1、三叉链表思路与具体实现

1.1、思路

  什么是三叉链表，无非就是多了一个指向父结点的指针，因此需要在结构体定义中增加这行代码：struct BiNode* parent;。 具体作用就是为二叉树中每个结点增加一个父结点属性，方便我们找到其中任意一个结点的直接前驱，下面来看具体实现。

1.2、代码实现

三叉链表存储结构：

#include
#include
typedef int ElemType;
typedef struct BiNode {
	ElemType data;
	struct BiNode* lchild, * rchild;
	struct BiNode* parent; // 父节点，存储当前结点的父节点
}BiNode ,*BiTree;

先序建立二叉树：

// 先序建立二叉树
void creat_BiTree(BiTree &T) {
	ElemType val;
	scanf("%d", &val);
	if (val == 0) return; // 输入0相当于空结点
	T = (BiTree)malloc(sizeof(BiNode));
	T->data = val;
	// 初始化指针指向
	T->lchild = NULL;
	T->rchild = NULL;
	T->parent = NULL;
	creat_BiTree(T->lchild);
	creat_BiTree(T->rchild);
}

为父节点赋值：

// 给父节点赋值
void val_parent(BiTree &T) {
	if (T == NULL) return;
	BiTree L = T; // 用于给左孩子赋值
	BiTree R = T; // 用于给右孩子赋值
	if (L->lchild) {
		L = L->lchild;
		L->parent = T;
	}
	if (R->rchild) {
		R = R->rchild;
		R->parent = T;
	}
	val_parent(T->lchild); // 递归左孩子
	val_parent(T->rchild); // 递归右孩子
}

中序遍历：

// 中序遍历
void inOrder(BiTree T) {
	if (T != NULL) {
		inOrder(T->lchild);
		printf("%-3d", T->data); // 左对齐，三个空格打印
		inOrder(T->rchild);
	}
}

打印父节点：

// 打印父节点
void print_parent(BiTree T) {
	if (T) {
		if (T->parent) printf("%-3d", T->parent->data);
		print_parent(T->lchild);
		print_parent(T->rchild);
	}
}

主函数调用：

int main() {
	BiTree T;
	creat_BiTree(T); // 先序创建二叉树
	inOrder(T); // 中序遍历检验是否正确
	printf("\n");
	val_parent(T); // 为父结点赋值
	print_parent(T); // 打印各结点的父结点
}

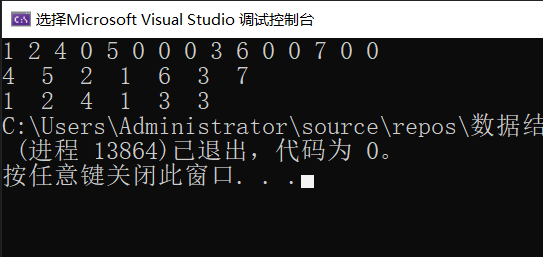
输入 1 2 4 0 5 0 0 0 3 6 0 0 7 0 0查看运行效果：

对应的二叉树为：

2、三种线索二叉树的实现

为什么会有线索二叉树的定义呢？

从逻辑上来看：
二叉树可以说是一个递归结构，想查找某个结点的前驱就只能从头开始递归，时间开销很大。如果给一个二叉树增加上前驱或者后继线索，那么我们就能立刻找到一个结点的前驱或者后继结点，提高了效率。

注：这里提到的前驱和后继对应着某种顺序，需要和 前中后序 结合。

从存储结构来看：

用一个满二叉树举例，假设有 $n$个结点，那么就会有$2n$个链域，会用掉$n-1$个链域，
那么剩下的 $n+1$个空链域就可以用来存储 “线索” 。怎么区别两个结点之间是线索还是真的物理相连呢？那就是增加标志位 ltag 和 rtag，标志位等于0代表着真正相连的结点，等于1代表着线索（初始化时的标志位都为0）。

注：由于前面已经实现了三叉链表，下面不再展示递归创建二叉树的代码。

2.1、中序线索二叉树实现

线索二叉树的存储结构：

typedef int Elemtype;
typedef struct ThreadNode{
	Elemtype data; 
	struct ThreadNode* lchild, * rchild; 
	int ltag, rtag; // 左右线索标志 tag==0 表示指向孩子， tag==1 表示指向线索
}ThreadNode,*ThreadTree;

核心函数 visit：

ThreadTree pre = NULL; // 全局指针pre，用来指向当前访问结点的前驱结点
void visit(ThreadTree& q) {
	if (q->lchild == NULL) {
		q->lchild = pre;
		q->ltag = 1;
	}
	if (pre != NULL && pre->rchild == NULL) {
		pre->rchild = q;
		pre->rtag = 1;
	}
	pre = q;
}

具体创建过程：

// 中序线索化
void InThread(ThreadTree T) {
	if (T != NULL) {
		InThread(T->lchild); 
		visit(T); // 在中间调用
		InThread(T->rchild); 
	}
}

// 创建中序二叉树
void CreatInThread(ThreadTree T) {
	pre = NULL;
	if (T != NULL) {
		InThread(T);
		pre->rchild = NULL;
		pre->rtag = 1; // 最后的pre 一定指向最后一个结点，直接将右孩子线索改为1
	}
}

2.2、先序线索二叉树实现

存储结构与核心函数不再展示。

具体创建过程：

// 先序线索化
void PreThread(ThreadTree T) {
	if (T != NULL) {
		visit(T); // 在前面调用
		if (T->ltag == 0) 
		    // 只有ltag 为0时才是真正的左孩子，不为0时则为线索
		    // 这里是为了防止调用访问过的前序前驱，无限递归
			PreThread(T->lchild);
		PreThread(T->rchild);
	}
}

// 创建先序线索二叉树
void creatPreThread(ThreadTree T) {
	pre = NULL;
	if (T != NULL) {
		PreThread(T);
		if (pre->rchild == NULL) pre->rtag = 1; // 处理最后一个结点
	}
}

2.3、后序线索二叉树实现

存储结构与核心函数不再展示。

具体创建过程：

// 后序线索化
void PostThread(ThreadTree T) {
	if (T != NULL) {
		PostThread(T->lchild);
		PostThread(T->rchild);
		visit(T); // 在后面调用
	}
}

// 创建后序线索二叉树
void creatPostThread(ThreadTree T) {
	pre = NULL;
	if (T != NULL) {
		PostThread(T);
		if (pre->rchild == NULL) pre->rtag = 1;
	}
}

3、中序线索二叉树的非递归遍历

  中序线索二叉树可以找到中序前驱和中序后继，而前序线索二叉树无法找到先序前驱，后序线索二叉树无法找到后序后继（非要找也可以，采用三叉链表或者从头遍历）。
  因此在这里展示非递归的遍历二叉树方法，时间复杂度：$O(1)$。

3.1、顺序中序遍历

// 找到以p为根结点的子树中第一个被中序遍历的结点，在 nextNode 函数里传入 p->rchild
ThreadTree firstNode(ThreadTree p) {
	// 循环找到最左子树
	while (p->ltag == 0) p = p->lchild;
	// 不用担心 p 为 NULL，因为ltag 如果为1，说明该结点已经是叶子节点，链域用来做线索
	return p;
}

//在中序线索二叉树中找到结点 p 的中序后继结点
ThreadTree nextNode(ThreadTree p) {
	if (p->rtag == 1)
		return p->rchild; //如果是线索的后继，直接返回
	else 
		return firstNode(p->rchild); //如果不是线索后继，循环找到最左下结点
}

// 非递归中序遍历
void Inorder(ThreadTree T) {
	for (ThreadTree p = firstNode(T); p != NULL; p = nextNode(p)) {
		printf("%d ", p->data);
	}
	printf("%\n");
}

3.2、逆序中序遍历

// 找到以 p 为根的子树中，最后一个被中序遍历的结点,在 beforeNode 函数里传入p->lchild
ThreadTree lastNode(ThreadTree p) {
	// 循环找到最右子树
	while (p->rtag == 0) p = p->rchild;
	return p;
}

// 中序线索二叉树找结点 p 的中序前驱
ThreadTree beforeNode(ThreadTree p) {
	if (p->ltag == 1)
		return p->lchild;
	else
		return lastNode(p->lchild);
}

// 对中序线索二叉树进行逆向中序遍历
void RevInorder(ThreadTree T) {
	for (ThreadTree p = lastNode(T); p != NULL; p = beforeNode(p)) {
		printf("%d ", p->data);
	}
	printf("%\n");
}

---

  线索二叉树这种存储结构无疑提高了查找结点直接前驱和直接后继的效率，但是注意前序线索二叉树会出现 死递归 的问题。