理解和实现简单的XOR神经网络
本文介绍了神经网络的基本知识,并以实现一个简单的XOR神经网络为例,详细解释了神经网络的工作原理和关键概念。我们将利用Python编写的代码来逐步理解并实现这个神经网络。
神经网络是一种模仿生物神经系统的计算模型,用于处理复杂的输入数据。本文将通过实现一个简单的多层感知器(MLP)神经网络,帮助读者理解神经网络的基本原理和关键概念。
神经网络基本构成
一个神经网络由多个层组成,每一层都包含若干神经元。这些层可以分为输入层、隐藏层和输出层。输入层接收输入数据,隐藏层负责处理数据,输出层生成最终结果。在我们的例子中,我们将实现一个具有2个输入节点、1个隐藏层(包含2个节点)和1个输出节点的神经网络。
激活函数
激活函数是神经元的关键组成部分,用于将神经元的输入值映射到一个特定的输出值。本例中,我们使用Sigmoid函数作为激活函数。Sigmoid函数将输入值映射到0到1之间的输出值。
反向传播算法
反向传播算法(Backpropagation)是训练神经网络的核心算法。在训练过程中,神经网络通过调整权重和偏置来学习输入数据与目标输出之间的映射关系。反向传播算法的关键思想是通过计算损失函数对权重和偏置的梯度,然后根据梯度来更新权重和偏置。
损失函数
损失函数用于衡量神经网络的输出与目标输出之间的误差。在本例中,我们使用均方误差作为损失函数。神经网络的目标是最小化损失函数。
代码实现
我们的代码实现了一个简单的XOR神经网络。首先,我们定义了激活函数及其导数。然后,我们初始化了神经网络的权重和偏置。接下来,我们使用一个循环进行训练,每次迭代中都使用反向传播算法更新权重和偏置。
本代码实现的XOR神经网络涵盖了以下知识点:
代码含有下列知识点:
- 神经网络的基本结构(输入层、隐藏层和输出层)
- 激活函数(Sigmoid函数)
- 反向传播算法
- 损失函数(均方误差)
- Python代码实现
在训练过程中,我们记录了每个迭代步骤的损失值。训练完成后,我们使用matplotlib库绘制损失值与迭代次数的折线图。
import numpy as np
# 定义激活函数和它的导数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(x):
return x * (1 - x)
# XOR输入和输出
X = np.array([[1, 0],
[0, 1],
[0, 0],
[1, 1]])
y = np.array([[1],
[1],
[0],
[0]])
# 初始化神经网络超参数
input_nodes = 2
hidden_nodes = 2
output_nodes = 1
learning_rate = 0.5
iterations = 10000
import matplotlib.pyplot as plt
# 初始化权重和偏置
np.random.seed(0)
weights_input_hidden = 2*np.random.rand(input_nodes, hidden_nodes)-1
weights_hidden_output = 2*np.random.rand(hidden_nodes, output_nodes)-1
bias_hidden = 2*np.random.rand(hidden_nodes, 1)-1
bias_output = 2*np.random.rand(output_nodes, 1)-1
# 在初始化权重和偏置之后添加此行
loss_values = []
# 训练神经网络
for i in range(iterations):
# 前向传播
hidden_layer = sigmoid(np.dot(X, weights_input_hidden) + bias_hidden.T)
output_layer = sigmoid(np.dot(hidden_layer, weights_hidden_output) + bias_output.T)
# 计算输出层误差
output_error = y - output_layer
output_delta = output_error * sigmoid_derivative(output_layer)
# 计算隐藏层误差
hidden_error = np.dot(output_delta, weights_hidden_output.T)
hidden_delta = hidden_error * sigmoid_derivative(hidden_layer)
# 更新权重和偏置
weights_hidden_output += learning_rate * np.dot(hidden_layer.T, output_delta)
weights_input_hidden += learning_rate * np.dot(X.T, hidden_delta)
bias_hidden += learning_rate * np.sum(hidden_delta, axis=0).reshape(-1, 1)
bias_output += learning_rate * np.sum(output_delta, axis=0).reshape(-1, 1)
# 在训练神经网络的循环中,更新权重和偏置之后添加此行
loss_values.append(np.mean(np.square(output_error)))
# 测试神经网络
print("测试结果:")
test_result = sigmoid(np.dot(sigmoid(np.dot(X, weights_input_hidden) + bias_hidden.T), weights_hidden_output) + bias_output.T)
print(np.round(test_result))
# 在测试神经网络之后添加以下内容
plt.figure()
plt.plot(range(1, iterations + 1), loss_values)
plt.xlabel('Epochs')
plt.ylabel('Loss Value')
plt.title('Loss Value vs. Epochs')
plt.show()
# 打印测试神经网络
print("打印测试结果:")
test_result = sigmoid(np.dot(sigmoid(np.dot(X, weights_input_hidden) + bias_hidden.T), weights_hidden_output) + bias_output.T)
rounded_test_result = np.round(test_result)
for i in range(X.shape[0]):
print(f"For input {X[i]} output is {rounded_test_result[i][0]}")
输出结果如下:
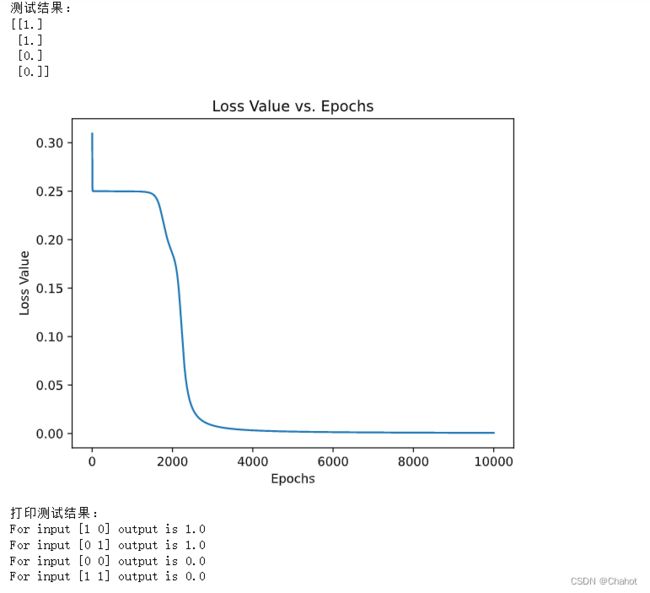
通过本文的介绍和代码实现,我们了解了神经网络的基本原理和关键概念。我们实现了一个简单的XOR神经网络,展示了如何使用神经网络进行数据处理和预测。尽管这个例子较为简单,但它涵盖了神经网络的基本概念,有助于读者建立对神经网络的初步认识。
在实际应用中,神经网络可以处理更复杂的问题和数据。为了解决更高级的问题,我们可以增加隐藏层的数量、调整激活函数或者使用不同的优化算法。神经网络在诸如图像识别、自然语言处理和语音识别等领域有广泛的应用。通过深入学习和实践,我们可以利用神经网络解决更多实际问题。