快速排序画图细致讲解,java代码实现(递归、栈两种方式)
前言
快速排序的定义:快速排序
当然严谨科学描述是比较枯燥的,大意就是(以从小到大为例):
- 在需要排序的数组中任取一个基准值(pivot),遍历这个数组中所有元素,将比基准值小的放在基准值左边,将比基准值大的基准值右边。
- 将数组按照 头、基准值位置、尾分成两段,即当成两个数组,对两个子数组重复步骤1
- 重复步骤1,2,直到数组不可再分,数组即为有序
图像说明:
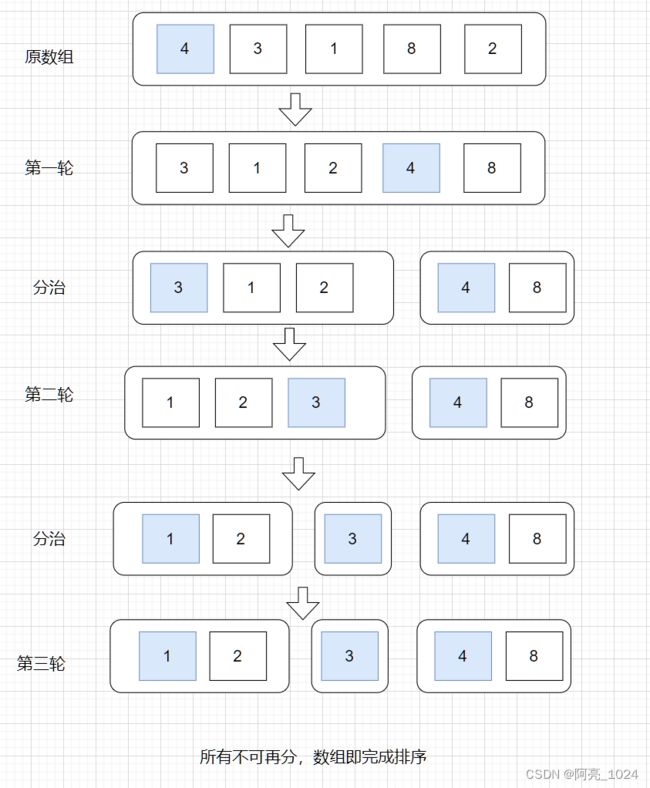
快排用到了分治的思想,即把一个问题分成若干个小问题,小问题就变得简单,当解决了所有小问题时,大问题也就迎刃而解。
一尺之棰,日取其半,不同的是,取半没有终点,但是快排这里有,当数组不可再分即为终点。
递归实现
通过上面的描述,肯定第一时间想到的就是递归实现,因为这个场景太复合递归了。
自己实现
下面我先给出我自己最开始的实现(不是最优),然后再给出一些比较优秀的实现,再进行比较,人家优秀在那里。如果只想看优秀的解法,可以跳这节
代码如下:
public void MyQuickTest() {
int[] ints = {4, 3, 1, 7, 2, 9};
// int[] ints = {4, 5, 3, 1, 0, 2, 7, 6, 8, 9};
int[] ints1 = myQuickRecursion(ints);
System.out.println(Arrays.toString(ints1));
}
// 快速排序,使用递归方式
public int[] myQuickRecursion(int[] ints) {
int len;
if (ints == null || (len = ints.length) <= 1)
return ints;
return myQuickRecursion(ints, 0, len - 1);
}
//
public int[] myQuickRecursion(int[] ints, int start, int end) {
// 对数组的安全检查
if (ints == null || ints.length <= 1 ) {
return ints;
}
// 数组不可再分的结束条件
if (start + 1 >= end) {
return ints;
}
// 找基准点,此处将数组第一个元素设置为基准点
int pivot = start;
// 遍历与基准点进行比较
for (int i = start + 1; i <= end; i++) {
// 大于基准值,交换分两种情况,一种是旁边,一种是非旁边
if (ints[i] < ints[pivot]) {
if (i == pivot + 1) {
int tem = ints[i];
ints[i] = ints[pivot];
ints[pivot] = tem;
} else {
int tmp1 = ints[pivot];
int tmp2 = ints[pivot + 1];
ints[pivot] = ints[i];
ints[pivot + 1] = tmp1;
ints[i] = tmp2;
}
// 交换了位置,那么基准值的位置
pivot += 1;
}
}
// 将数组按照 头、基准值位置、尾分成两段
// 左边
myQuickRecursion(ints, start, pivot - 1);
// 右边
myQuickRecursion(ints, pivot + 1, end);
// 排序完成
return ints;
}
自己在实现过程中,也是边调试边改,才写出来这一版。使用递归代码也不多,这儿代码比较多的是:当遍历的元素比基准值小时,应该交换到基准值的左边,这个交换的代码比较多,这是因为我这儿处理时,交换分为两种情况:
- 需要交换的元素就在基准值的旁边
- 需要交换的元素不在基准值的旁边
画图说明

3和1,在与基准值交换时,是直接交换的,而2不同,需要多一些步骤。
上图解释了第一轮示意图,第二轮按照同样的方式处理{1,2,3}和{7,9},再处理第三轮,完成排序。
优秀实现
上面我自己的实现,逻辑没问题,代码也没问题,但是将小值放到基准值左边有更好的处理方式。我上边的处理方式是:如果目标值比基准值小,就要将基准值的位置移动,所以才有了目标值是否在基准值旁边这样的判断,但实际上有更好的处理方式。
单边循环法
就是先不动基准值,用一个辅助指针标基准值应该在的位置,如果遍历到基准值更小的值,就将目标值和辅助指针指向的值交换位置。
图例说明如下:
第二轮按照同样的方式处理{1,2,3}和{7,9},再处理第三轮,完成排序。
代码如下
public static void main(String[] args) {
int[] arr = new int[]{4, 4, 6, 5, 3, 2, 8, 1};
// int[] arr = new int[]{4, 3, 1, 7, 8, 9};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
public static void quickSort(int[] arr, int startIndex, int endIndex) {
// 递归结束条件:startIndex大于或等于endIndex时
if (startIndex >= endIndex) {
return;
}
// 得到基准元素位置
int pivotIndex = partition(arr, startIndex, endIndex);
// 根据基准元素,分成两部分进行递归排序
quickSort(arr, startIndex, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, endIndex);
}
/**
* 分治(单边循环法)
*
* @param arr 待交换的数组
* @param startIndex 起始下标
* @param endIndex 结束下标
*/
private static int partition(int[] arr, int startIndex, int endIndex) {
// 取第1个位置(也可以选择随机位置)的元素作为基准元素
int pivot = arr[startIndex];
// 辅助指针,标记下一个比pivot大的值应该放的位置(mark+1)
int mark = startIndex;
// 遍历,从startIndex下一个开始,一一与pivot值进行比较,如果比pivot小,就将mark指针++,并且将较小值换到指定位置
for (int i = startIndex + 1; i <= endIndex; i++) {
if (arr[i] < pivot) {
mark++;
int p = arr[mark];
arr[mark] = arr[i];
arr[i] = p;
}
}
// 遍历完成,将第一个,即pivot与mark指针进行交换
arr[startIndex] = arr[mark];
arr[mark] = pivot;
return mark;
}
此方式相比自己的实现,优点有:
- 自己实现的方式,在遍历时,将基准值pivot拖着一起往后走,增加了额外的交换。而此方式不移动pivot,而是用辅助指针mark标记pivot应该在的位置,一轮结束时,才将mark和pivot进行交换,减少了交换次数
- 自己的实现,需要区分遍历的目标元素和pivot的位置关系,存在两种不同方式的交换,代码量多,而且不易理解,此方式代码量更少且更易理解。
在上面画图解释的过程中就已经发现,当遍历到的元素比pivot小时,需要进行交换,但是如果此时mark+1 = i,那么交换其实是本身和本身交换,可以在代码中多增加一层判断,如果是此种情况,可以只让mark后移,而不进行交换。
双边循环法
顾名思义,就是用两个指针,两边同时遍历,从左边找比基准值大的值,从右边找比基准值小的值,找到之后交换,直到两个指针相遇,结束一轮,分治进行下一轮。
图例:
待补充
代码:
public static void main(String[] args) {
int[] arr = new int[]{4, 4, 6, 5, 3, 2, 8, 1};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
public static void quickSort(int[] arr, int startIndex, int endIndex) {
// 递归结束条件:startIndex大于或等于endIndex时
if (startIndex >= endIndex) {
return;
}
// 得到基准元素位置
int pivotIndex = partition(arr, startIndex, endIndex);
// 根据基准元素,分成两部分进行递归排序
quickSort(arr, startIndex, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, endIndex);
}
/**
* 分治(双边循环法)
* @param arr 待交换的数组
* @param startIndex 起始下标
* @param endIndex 结束下标
*/
private static int partition(int[] arr, int startIndex, int endIndex) {
// 取第1个位置(也可以选择随机位置)的元素作为基准元素
int pivot = arr[startIndex];
int left = startIndex;
int right = endIndex;
while (left != right) {
//控制right 指针比较并左移
while (left < right && arr[right] > pivot) {
right--;
}
//控制left指针比较并右移
while (left < right && arr[left] <= pivot) {
left++;
}
//交换left和right 指针所指向的元素
if (left < right) {
int p = arr[left];
arr[left] = arr[right];
arr[right] = p;
}
}
//pivot 和指针重合点交换
arr[startIndex] = arr[left];
arr[left] = pivot;
return left;
}
使用栈
栈和递归都具有回溯性质,递归大部分情况都能使用栈+循环来代替,此处也不例外。
比如我自己的实现,使用栈,代码如下:
public void myQuickStackTest() {
// int[] ints = {4, 3, 1, 7, 8, 9};
int[] ints = {4, 5, 3, 1, 0, 2, 7, 6, 8, 9};
int[] ints1 = myQuickStack(ints);
System.out.println(Arrays.toString(ints1));
}
public int[] myQuickStack(int[] ints) {
int len;
if (ints == null || (len = ints.length) <= 1) return ints;
Stack<Integer> stack = new Stack<>();
int begin = 0;
int end = len - 1;
int pivot;
while (!stack.isEmpty() || begin+1 < end) {
if (begin+1 < end) {
pivot = begin;
// 进行归并,并移动pivot
for (int i = begin + 1; i <= end; i++) {
// 大于基准值,交换分两种情况,一种是旁边,一种是非旁边
if (ints[i] < ints[pivot]) {
if (i == pivot + 1) {
int tem = ints[i];
ints[i] = ints[pivot];
ints[pivot] = tem;
} else {
int tmp1 = ints[pivot];
int tmp2 = ints[pivot + 1];
ints[pivot] = ints[i];
ints[pivot + 1] = tmp1;
ints[i] = tmp2;
}
pivot += 1;
}
}
// 移动pivot并加1
pivot += 1;
// 将右边存入栈中
stack.push(end);
stack.push(pivot);
end = pivot;
}else {
begin = stack.pop();
end = stack.pop();
}
}
return ints;
}
使用栈的单边循环和双边循环,改造方式也很简单
单边循环使用栈,代码:
// 待补充
双边循环使用栈,代码:
// 待补充
