LeetCode算法小抄 -- Kruskal 最小生成树算法

⚠申明： 未经许可，禁止以任何形式转载，若要引用，请标注链接地址。 全文共计2731字，阅读大概需要3分钟
更多学习内容， 欢迎关注【文末】我的个人微信公众号：不懂开发的程序猿
个人网站：https://jerry-jy.co/

阅读 Kruskal 最小生成树算法 之前需要先学习 并查集算法

经典图论算法

Kruskal 最小生成树算法

什么是最小生成树

最小生成树（Minimum Spanning Tree）算法主要有 Prim 算法（普里姆算法）和 Kruskal 算法（克鲁斯卡尔算法）两种

先说「树」和「图」的根本区别：树不会包含环，图可以包含环。

如果一幅图没有环，完全可以拉伸成一棵树的模样。说的专业一点，树就是「无环连通图」。

那么什么是图的「生成树」呢，其实按字面意思也好理解，就是在图中找一棵包含图中的所有节点的树。专业点说，生成树是含有图中所有顶点的「无环连通子图」。

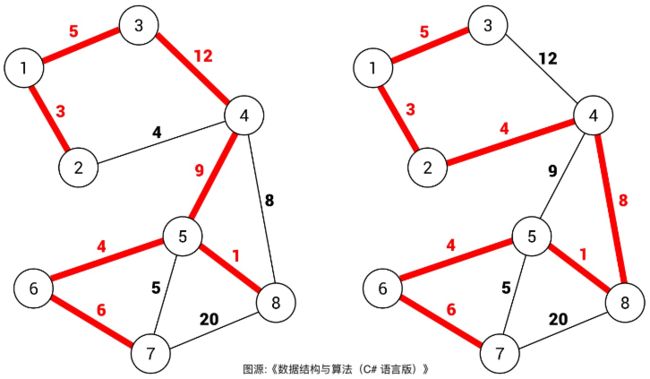
一幅图可以有很多不同的生成树，比如下面这幅图，红色的边就组成了两棵不同的生成树

对于加权图，每条边都有权重，所以每棵生成树都有一个权重和。比如上图，右侧生成树的权重和显然比左侧生成树的权重和要小。

所有可能的生成树中，权重和最小的那棵生成树就叫「最小生成树」。

一般来说，我们都是在无向加权图中计算最小生成树的，所以使用最小生成树算法的现实场景中，图的边权重一般代表成本、距离这样的标量。

在构造最小生成树的过程中，你首先得保证生成的那玩意是棵树（不包含环）对吧，那么 Union-Find 算法就是帮你干这个事儿的。

所谓最小生成树，就是图中若干边的集合（我们后文称这个集合为mst，最小生成树的英文缩写），你要保证这些边：

1、包含图中的所有节点。

2、形成的结构是树结构（即不存在环）。

3、权重和最小。

前两条其实可以很容易地利用 Union-Find 算法做到，关键在于第 3 点，如何保证得到的这棵生成树是权重和最小的。

这里就用到了贪心思路：

将所有边按照权重从小到大排序，从权重最小的边开始遍历，如果这条边和mst中的其它边不会形成环，则这条边是最小生成树的一部分，将它加入mst集合；否则，这条边不是最小生成树的一部分，不要把它加入mst集合。

1584. 连接所有点的最小费用

给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。

解法思路就是先生成所有的边以及权重，然后对这些边执行 Kruskal 算法即可：

class Solution {
    public int minCostConnectPoints(int[][] points) {
        int n = points.length;
        // 生成所有边及权重
        List<int[]> edges = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                int xi = points[i][0], yi = points[i][1];
                int xj = points[j][0], yj = points[j][1];
                // 用坐标点在 points 中的索引表示坐标点
                edges.add(new int[] {
                    i, j, Math.abs(xi - xj) + Math.abs(yi - yj)
                });
            }
        }
        // 将边按照权重从小到大排序
        Collections.sort(edges, (a, b) -> {
            return a[2] - b[2];
        });
        // 执行 Kruskal 算法
        int mst = 0;
        UF uf = new UF(n);
        for (int[] edge : edges) {
            int u = edge[0];
            int v = edge[1];
            int weight = edge[2];
            // 若这条边会产生环，则不能加入 mst
            if (uf.connected(u, v)) {
                continue;
            }
            // 若这条边不会产生环，则属于最小生成树
            mst += weight;
            uf.union(u, v);
        }
        return mst;
    }
}
class UF {
    // 连通分量个数
    private int count;
    // 存储每个节点的父节点
    private int[] parent;

    // n 为图中节点的个数
    public UF(int n) {
        this.count = n;
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }
    
    // 将节点 p 和节点 q 连通
    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        
        if (rootP == rootQ)
            return;
        
        parent[rootQ] = rootP;
        // 两个连通分量合并成一个连通分量
        count--;
    }

    // 判断节点 p 和节点 q 是否连通
    public boolean connected(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        return rootP == rootQ;
    }

    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    // 返回图中的连通分量个数
    public int count() {
        return count;
    }
}

Kruskal 算法的复杂度分析：

假设一幅图的节点个数为V，边的条数为E，首先需要O(E)的空间装所有边，而且 Union-Find 算法也需要O(V)的空间，所以 Kruskal 算法总的空间复杂度就是O(V + E)。

时间复杂度主要耗费在排序，需要O(ElogE)的时间，Union-Find 算法所有操作的复杂度都是O(1)，套一个 for 循环也不过是O(E)，所以总的时间复杂度为O(ElogE)。

–end–