贝叶斯分层模型应用之直播场景打分校准

1. 背景

精排预估打分是在线广告系统里非常重要的环节，其中打分准确性会极大地影响客户效果，也会影响用户体验和平台收益。精排预估打分为前链路打分和后链路打分，以 CPC（Cost Per Click）计费模式为例，前链路打分指点击率（Click-Through Rate，CTR），后链路打分指点击后客户获得的效果，这里的效果可以有很多种，常见的有成交量、收藏量等。

• 前链路打分主要用于广告排序：特指预估点击率（pCTR，predict CTR），平台按照 pCTR * bid_price 进行排序，pCTR 准确性影响排序的准确性。

• 后链路打分主要用于出价决策：比如预估成交率（pCVR，predict CVR），OCPX（Optimized Cost Per X）自动出价模式下，出价和后链路打分相关，因此打分的准确性直接影响客户最终投放效果。另外，BCB 以及 MCB 模式下也使用了后链路打分，打分准确是 BCB、MCB 最优性成立的基本条件。

精排预估打分模型主要采用深度模型，对特征、样本、模型结构的挖掘工作持续迭代，经过不断优化，打分精度也不断再创新高，尽管如此，精排预估打分仍然存在一些问题。

• 序准确 or 值准确：一般而言，精排打分模型多数看的是 AUC 指标，AUC 指标对应序的准确性，对于值的准确性容易被忽视，比如 A 渠道统计 CTR 是 B 渠道的 2 倍，如果值是准确的，那么打分也应该为近似 2 倍的关系。

• 冷启动：这里的冷启动包括新客户冷启动和新渠道冷启动，这部分流量缺少历史样本，精排预估打分准度受限。

• 维度效果差异巨大：某些维度下的效果存在很大差异，精排模型精准地学到这些倍数关系非常困难。尤其是流量渠道维度，好渠道的 CVR 可能是差渠道 CTR 的几十倍。

• 样本倾斜：大多数场景存在长尾效应效应，例如大占比数量的流量渠道的样本量占比较低，由于精排模型统一建模，或多或少存在少样本“迁就”多样本现象。

校准是解决以上问题最直观、最直接的方法，也是业界常用的方法。它的思路很简单，就是在精排模型打分阶段后对打分进行修改，后续机制策略使用校准后的分，流程图如下：

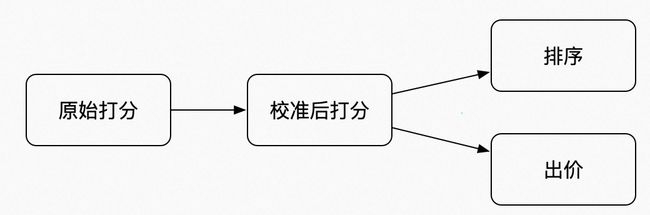
一般而言，校准模块需要要具备以下特点：

• 简单轻量：根据定位一可知，校准模块不做重度优化，设计理应简单轻量。

• 可解释：一方面，可解释意味着合情合理，badcase 可能会少，或者出现 badcase 更容易排查，另一方面，校准结果的解释性可为精排模型提供优化思路。

• 鲁棒&风险可控：校准模块承担着为精排模型保驾护航的作用，需要降低校准后效果更差的风险。

2. 问题分析

我们之所以认为精排模型存在值准度问题，大多数情况是因为在做一些数据统计分析的时候，发现某些维度的打分不满足直观的统计特性，如下图所示：

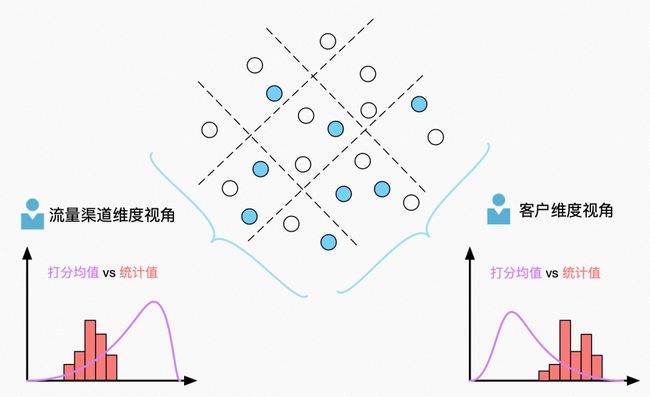
实际角度来看，不管是流量渠道维度和客户维度，统计值和预估值存在较大差异。我们可以通过统计学假设检验来解释这个问题，以 CTR 打分为例，我们挑选了一些打分值都为 9.07% 的实际样本，总样本量为 444587，正样本量为 36267。原假设为「所有样本真实 CTR 都为 9.07%」，这里我们采用正样本量作为统计量，此时正样本量服从 n = 444587，p = 0.0907 的二项分布，我们很容易计算。，显而易见我们要拒绝原假设，通俗的解释就是如果原假设成立出现这种样本的几率几乎为 0。原假设被拒绝意味着至少一部分样本 CTR 不是 9.07%。

由于无法确切知道每个样本的真实 CTR，统计推断结论基本只能到这一步，即「我们知道打分有问题，但不知道哪些样本有问题」，此时校准就显得有必要了。

业界常用的校准算法中，非参数方法能做到自适应，但方法复杂一点则缺乏一定的可解释性；参数方法可解释，但目前存在的建模不够复杂，表达能力不足；混合方法看起来能取长补短，但如何结合存在一定的 trick，策略联动没有理论的必然性。因此，这里我们使用了贝叶斯分层模型，相对于参数方法，模型更复杂更具有表达性，相对于混合方法，又能将贝叶斯统计理论贯彻到底，达成一体化建模的目的。

贝叶斯分层模型具有以下特点：

• 纯粹的贝叶斯概率统计模型，显式建模，最终产出是参数后验分布；

• 使用层次参数结构，增加了共性和个性的表达能力，具备一定泛化性，也允许字段缺失；

• 贝叶斯模型产出的参数后验分布，使得具有风险决策的能力。

3. 建模方案

为了让校准工作能够顺利开展，需要做 bias 一致性假设，即「在确定的维度值条件下，所有样本打分具有固定的偏差」。概率模型校准的思路比较直接，即通过概率建模，利用有限的样本推断每个维度下的 bias，形式化如下：

这里使用 ln 的原因是使得 bias 具备相对偏差的概念，举个例子，bias = -0.05，意味着 pctr 大概高估了 5%。

这里的维度是指某种样本切分的规则，维度值是指按照这个切分规则下的一个聚簇。例如，「客户 * 渠道 * 打分区间」表达了一种维度，「客户 A、渠道 B、打分 0.01~0.02 之间」表达了该维度下的一个值。对于维度的选择需要一定的经验，一般和具体业务相关，如果维度数量过少，基本假设成立的可能性越低，校准效果有限；如果维度数量越多，bias 参数越多，模型越复杂，而且平均每个维度的样本就稀疏，最终也会影响校准精度。实际情况下，一般需要进行折中，即只选取少量重要的维度。

为了方便理解，这里我们由简到繁、循序渐进介绍各种建模方法，如下：

• 全局维度：所有样本归为一个维度，最简单，效果也有限。

• 独立维度建模：在全局维度基础上增加分层概念，不同客户的样本 bias 不同，最终模型具有一定的泛化性和解释性，解决了传统机器学习面临的样本倾斜问题；另外，在客户分层维度的基础上，增加独立的流量渠道维度，模型表达能力更高。

• 交叉维度建模：增加客户、流量渠道交叉维度，解决客户、流量渠道对 bias 的作用不独立的情况。

• 直播广告场景建模实践：这一小节以直播广告场景为例介绍建模方法。

3.1 全局维度建模

全局维度是最简单的建模方式，即所有样本都归为一个维度，bias 全局唯一，建模如下：

其中 y 为真实 ctr，r 为 pctr，为 bias

根据贝叶斯理论，我们可以引入先验，即：

最终概率盘式图（Plate Notation）如下：

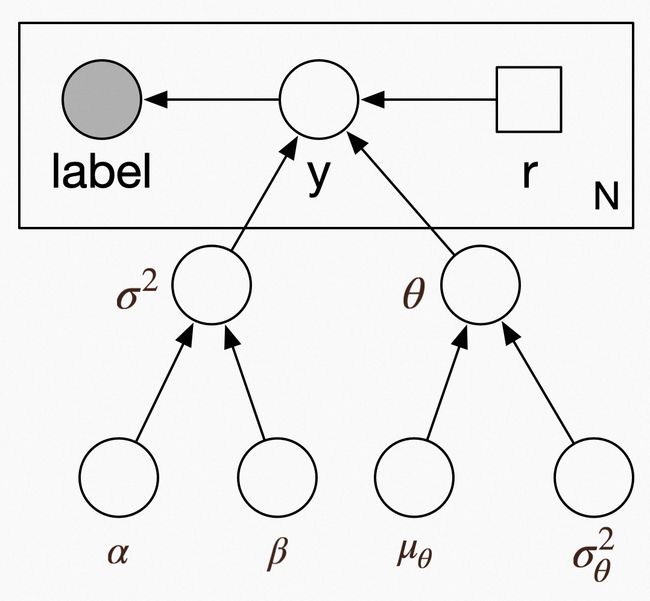其中 N 为样本量，label 为观测到的样本点击与否

由于这是一个线性模型的特例，为了方便表达， 这里我们使用线性模型独有的表达方式，如下所示：

解释如下：

• 波浪线左侧为目标部分，右侧为效应部分；

• 效应以符号 + 分隔，目标等于所有效应项之和加上残差项，残差项默认自带，因此可省略不写；

• 效应 = factor * parameter，由于 parameter 默认自带，我们只用写 factor，factor = 1 表示该项为截距项；

• 例如，表达的含义为 。

上面表达式表达的含义为 ，和可省略，因此右侧写成 1。

实际我们使用全局维度的意义不大，一方面，维度太少 bias 一致性假设成立可能性低，另一方面，实际总样本量一般非常充足，使用纯规则统计的方式就能得到非常置信的结果，没有必要通过模型来推断。

3.2 独立维度建模

为了增加模型的表达能力，我们需要增加一些维度。以客户维度为例，每个客户应具有不同的 bias，最简单的方法是按照 3.1 小节的方法建 M 个独立模型（M为客户数）但这种方法存在问题，不同客户样本不一样，有些客户样本比较稀疏，此时模型就会极度依赖先验，那么问题来了，不同客户的先验参数怎么确定。

目前最直接可行的方法就是假设所有的客户先验参数一样，即共用先验参数，这么做也具备很好的泛化性和解释性。例如，某个客户没有样本或者样本很少，此时我们需要大部分参照先验，然而先验是综合所有客户计算出来的，已经能够充分表达所有客户“平均”的情况，合情合理。

既然我们把所有客户的先验参数统一起来，那么最初我们讨论的「M 个独立模型」这个概念就不复存在了，因为它们都共享了先验参数，此时使用一个模型就能表达，即分层模型，具体建模如下：

表示客户 i 的 bias，且这个样本属于客户 i，和 为共享的参数。概率盘式图表达如下：

我们可以把 代入到目标式子里面，得到另外一种等价的建模，即混合效应模型（Mixed-Effects Model，https://en.wikipedia.org/wiki/Mixed_model），如下：

不同领域对层次模型的称呼习惯不同，比如社会学通常叫分层线性模型（multilevel linear model），生物统计研究经常使用混合效应模型（mixed-effects model）和随机效应模型（rankdom-effects model），计量经济使用随机系数回归模型（random-coefficient regression model），统计学使用协方差成分模型（covariance components model）。

混合效应分为固定效应和随机效应，以上面的表达为例，截距项为固定效应，全局唯一，为随机效应项，和客户有关且满足总体均值为 0 的约束。通过转化为混合效应模型，我们能得到更为简洁的线性模型表达，如下：

和 3.1 小节相比，这里多了一个随机效应 ，中间竖线左侧仍然为 factor，竖线右侧表达了分组的概念，即不同的 customer 具有不同的 parameter，且服从总体均值为 0 的约束。

这个模型的统计解释性如下：

• 对于没有样本的新客，随机效应为 0，此时这个客户的打分 bias 均值等于固定效应；

• 对于样本较少的客户，由于随机效应参数有 0 均值约束，结合很少的样本，模型推断的随机效应应该为接近 0 的值，此时这个客户的打分 bias 均值基本接近固定效应；

• 对于样本较多的客户，模型推断的随机效应参数极大参照样本，此时这个客户的打分 bias 基本等于统计 bias（统计 ctr 除以打分均值）。

层次模型可以解决统计陷阱和样本倾斜的问题。举个例子，某个场景客户分为 3 类，头部客户、腰部客户和底层客户，他们的点击样本信息（构造数据）如下：

客户类型	客户数量	样本数量	统计 ctr
头部客户	100	1000w	0.1
腰部客户	1000	100w	0.03
尾部客户	5000	10w	0.01

那么，问题来了，假设来了一个新客户（无额外信息），他的 ctr 应该是多少？由于我们对这个客户一无所知，通常来看，我们使用大盘平均 ctr 作为新客户的 ctr 合情合理。何为大盘平均 ctr？按照日常统计数据的惯性思维，很容易就想到了样本统计微平均，即总样本点击量除以总样本量。以上表为例，大盘 ctr 平均值 = (1000w * 0.1 + 100w * 0.03 + 10w * 0.01) / (1000w + 100w + 10w) = 0.0928。但是，另外存在一种统计方式，即样本统计宏平均，这种方法以客户作为统计粒度，即大盘 ctr 平均值 = (100 * 0.1 + 1000 * 0.03 + 5000 * 0.01) / (100 + 1000 + 5000) = 0.0133。这两种统计方式得到的平均值截然不同，哪种统计更合理取决于问题的问法，如果问题是「假如来了一个曝光，它的 ctr 是多少？」，那么微平均合理，如果问题是「假如来了一个客户，它的平均 ctr 是多少？」，那么宏平均合理，很显然原始问题是属于后者。

同样精排模型训练数据使用的是最细粒度的样本，如果处理的不好很容易掉入上面描述的统计陷阱。校准可以针对这个问题设计分层模型结构，不同样本量的客户最终会在顶层参数拉齐（类似上面例子的宏平均统计方法），最终减少样本倾斜带来的影响。

同样，在客户基础上，我们可以增加更多的随机效应，比如流量渠道维度，具体建模如下：

其中 pid 为流量渠道的区分信息。

新建模使得不同 pid 具备不同变化的能力，如果不同的 pid 确实存在较大的 bias 差异，这种建模方式能提升校准效果。当然，这样建模存在假设，即 customer 和 pid 对应的随机效应参数是正交的，即同一个客户不同的 pid bias 分布都是一样的，同理，同一个 pid 不同客户的 bias 分布都是一样的。

另外，从模型结构上来看，增加了 pid 以后，这个模型已经不是严格意义上的分层结构（树状分层）了，但出于习惯问题，我们仍然称呼它为分层模型，这并不影响工作的开展。

3.3 交叉维度建模

有时候 3.2 小节的多维度参数正交的假设并不成立，比如存在某个客户某个 pid 的打分 bias 和其他的明显不同，此时使用独立维度建模就不能表达这种特例了。这里我们可以增加 customer 和 pid 的交叉维度，建模如下：

新随机效应项表达的含义为不同的 customer、pid 组合具有不同的参数，这些参数仍然满足 0 均值约束。这么做增加了 customer、pid 组合独立变化的能力，解决了 3.2 小节正交假设不成立问题。

到底假设正交还是假设不正交呢？如果真实情况是正交，实际却增加了交叉维度，这样会导致模型复杂度增加，不会产生更好的效果，但是从直觉上来看，完全正交的假设又不太可能。所以这里需要根据实际情况进行折中，一般而言如果样本足够多，现有模型使用的维度少，那么可以考虑增加交叉维度。

3.4 直播广告场景建模实践

直播广告场景下，采用以下建模方式：

其中 说明：

• 这里 表达的含义为所有的 customer、pid、r_level 组合组成的效应（包含固定效应），一共 个效应项，即 ：

• r_level 是 r 的离散化区间，使用 r_level 的原因是根据实际经验，不同打分区间的 bias 存在较大差异，某种意义上来讲，r_level 提供了一种非线性化校准能力。

这样建模其实是综合直播业务特点以及校准定位给出的折中方案，主要体现如下：

• 简单轻量：仅使用 customer、pid、r_level 三个维度，最终模型仅具有 8 个效应项，满足校准的简单轻量定位，定位问题简单。如果增加一个维度，效应项会翻倍（8 个变成 16 个），训练预测开销翻倍。当然，我们也可以不用维度全组合作为效应项，即挑选部分最有用的组合作为效应项，但这部分仍然在研究探索之中。

• 增加维度边际收益低：customer、pid、r_level 是肉眼可见 bias 存在较大差异的维度。实际角度而言，增加维度带来的效果并不明显。

4. 模型推断&校准流程

众所周知，复杂的贝叶斯模型最大的难点在于后验参数推断，这里我们使用了阿里妈妈开发的 BGLM（Bayes Generalized linear model）框架，使得贝叶斯推断变得简单。

BGLM 采用了 【Mean-Field】https://en.wikipedia.org/wiki/Mean-field_theory 变分推断，简单解释为，使用各个参数独立的分布代替复杂的联合后验分布，这个分布寻找的准则为新老分布的 KL 散度最小化，公式表达如下：

为近似分布，表达为 为真实贝叶斯后验分布

贝叶斯推断存在另外一大类方法，即 MCMC（Markov Chain Monte Carlo），https://en.wikipedia.org/wiki/Markov_chain_Monte_Carlo。变分推断相比 MCMC 最大的优势是收敛迅速（类似 EM 算法），20~30 轮就可收敛，资源占用较少，另外近似分布一般有具体的解析表达，利于进行后续决策推导，当然变分推断也存在一定缺陷，即分布是近似的，收敛后近似后验分布和真实后验分布存在固有 gap，但 MCMC 方法不存在这个问题，只要样本足够多就能无限概率逼近真实后验分布。

经过 BGLM 的变分推断，我们可以得到参数的后验近似分布。有了参数的后验近似分布，我们可以针对预测样本进行后验预测推断。得益于参数后验近似分布有具体形式化表达，预测样本的线性预测子（线性预测子为所有效应项之和）可以很容易推导，最终表达为高斯近似分布如下：

有了线性预测子的分布，我们可以很容易得到目标值分布，即：

引擎一般只接受一个值，而不是一个分布，因此我们需要额外进行打分决策，根据上面的结论，我们可以简单使用线性预测子的均值作为决策值（风险中性），即：

其中 为最终校准打分决策

到这里，我们就有了简单的校准流程：

1）构造训练样本，包含 label、打分以及相应特征；

2）使用 BGLM 对模型的参数进行贝叶斯后验推断，参数的变分近似后验分布即为“模型”；

3）在线来了一个预测样本，根据打分、特征调用 BGLM 预测模块，得到真实目标值的后验预测分布；

4）根据打分的后验预测分布进行打分决策。

5. 校准风险决策

根据 4 小节，我们给出了最简单的风险中性校准决策，即使用线性预测子的均值，但是这种方式抛弃了预测方差，对于方差较大的样本，存在校准结果变差的可能，因此这里提出了风险决策。

设观察数据为 D，预测样本为 S，校准打分 的后验预测概率密度为 。

一方面，我们希望决策的校准分尽量后验预测概率大（经验风险），可以表达为概率密度的熵，即：

另一方面，我们又希望最终校准后的分离原始分差异不要太大（校准幅度风险），校准幅度风险可表达为平方损失，如下：

两个风险函数结合起来组成我们最终的风险函数（为权重因子, ）。

我们的目标为寻找风险值最小的 r，即：

根据 6 小节可知，的形式为高斯分布，我们可以直接求出最优的 ，即：

可以看到：

• 当 时，，此时等价于风险中性校准，即使用均值作为决策值；

• 当 时，，等价于不校准；

• 当 很小时，说明数据充分，，此时很大程度参照模型推断结果；

• 当 很大时，说明数据不充分，，此时应该选择不校准。

6. 校准效果

这里介绍一下校准的评估指标：

• AUC：衡量序的准确性，精排模型关注的重点指标。

• GAUC（Grouped AUC）：由于 AUC 评估的是大盘，直播场景不同流量渠道正样本率差异非常大，AUC 经常能达到 0.9 以上，此时 AUC 很难反映流量渠道内部打分的准确性，GAUC 期望解决这类问题。它的计算方式为先按渠道计算 AUC，然后各个渠道的 AUC 再求平均。

• PCOC：即统计正样本率除以预估打分均值，PCOC = 1 最好，PCOC 大于 1 或者小于 1 表示打分存在问题。PCOC 指标粒度太粗，不能反应细节，因此不能过低依赖这个指标。

• ERROR_维度值：首先统计某个维度值下的样本的 PCOC，维度值示例：「流量渠道直播广场」， 计算方式：

  维度值维度值维度值维度值维度值

  。可以看到这个值越小越好，最好情况等于 0。

• ERROR_维度：维度示例「流量渠道」，它包含多个维度值。维度维度值维度维度值。当然某些维度值正样本不足，PCOC 波动较大，这里可以选择不参与计算。

目前来看，直播广告为校准的主要应用场景，前链路打分校准 ERROR 有 66% 的降幅，流量实验也能带来 5% 的收入提升；后链路打分（成交率、吸粉率等等）校准 ERROR 有 5~25% 不同程度的校准，转化成本有 2-19% 不同程度的降低，显著提升了客户体验。另外，经过调优后的校准风险决策大概能带来 ERROR 1-5% 的降幅。

7. 总结

针对直播场景精排打分值准确性、冷启动等问题，业界常用解决方案是打分校准。为了达成校准的目的，我们使用了基于纯贝叶斯理论的分层模型。一方面，贝叶斯分层模型简单轻量、可解释、可泛化；另一方面，贝叶斯后验分布天然提供了风险决策能力，降低了校准精度风险。实际角度来看，在直播广告场景下，贝叶斯分层模型带来了不错的效果。

END

也许你还想看

丨CBRL：面向ROI约束竞价问题的课程引导贝叶斯强化学习框架

丨AdaCalib: 后验引导的特征自适应预估校准

丨基于树模型的特征可感知的个性化校准方法

关注「阿里妈妈技术」，了解更多~

喜欢要“分享”，好看要“点赞”ღ~

↓欢迎留言参与讨论↓