SMC/VSC（十一）——基于趋近律的离散滑模控制(白嫖程序模型)

目录

前言

 1.被控对象

2.控制器设计

3.m语言仿真分析

3.1出图结果

4.S函数仿真分析

4.1控制器设计

​​4.2调参

4.3s函数编写被控对象

4.4s函数编写控制器

4.5仿真结果

---

前言

虽然滑模变结构控制主要是针对连续系统，因为只有理想的连续滑模变结构控制才有切换逻辑产生的等效控制ueq，对于离散系统只能产生准滑模动态，但是实际工程中，计算机控制均为离散系统，所以有必要学习一下离散滑模控制，而实现形式有两种，一种是通过m语言，另一种是通过s函数的离散更新函数建模分析实现。

首先，以常用的指数趋近律进行离散化，这里就不敲键盘了，这公式太难打了，这里直接附图片(仅作为学术交流，如有侵权请联系删除)。

 1.被控对象

以二阶系统为例：

2.控制器设计

取离散系统滑模面：

s(k) = C*x(k)

则其导数即：s(k+1) = C*x(k+1) = C*(A*x(k)+V*u(k))

由上述离散的滑模趋近律有：s(k+1)  = （1-q*T）*s(k)-ε*T*sign(s(k))，联立滑模导函数和趋近律，得离散滑模控制律为：

但是仅以状态变量为滑模函数变量，这样设计得到的控制律不具有鲁棒性(即抗扰动效果差或者难以实现跟踪)，以及可以看到需要精确的模型参数A、B；所以一般以误差变量为滑模函数变量，下面也会进行仿真实例分析。

3.m语言仿真分析

A=[1 0.0010;0 0.9753];
B=[-0.0001;-0.1314];
x=[0.5;0.5];%初始状态
ts=0.001;%采样时间/仿真时间间隔
for k=1:1:2000
    time(k)=k*ts;
    
    c=5;q=10;ep=0.5;%控制律调节参数
    C=[c 1];
    s(k)=C*x;%滑膜面 C*x(k),因为x0 = [0.5,0.5]'
    M = 1;
    if M==1            %符号函数作为切换函数
        u(k)=-inv(C*B)*(C*A*x-(1-q*ts)*s(k)+ep*ts*sign(s(k)));
    elseif M==2        %饱和函数作为切换函数
        delta=0.005;
        kk=1/delta;
        if s(k)>delta
            sats=1;
        elseif abs(s(k))<=delta
            sats=kk*s(k);
        elseif s(k)<-delta
            sats=-1;
        end
        u(k)=-inv(C*B)*(C*A*x-(1-q*ts)*s(k)+ep*ts*sats);
    end
    x = A*x+B*u(k);%x(k+1),更新
    x1(k) = x(1);%状态变量x1
    x2(k)=x(2);%状态变量x2
end
figure(1);
plot(time,x1,'r',time,x2,'k','linewidth',2);
xlabel('time(s)');ylabel('x1,x2');
title("状态变量变化曲线(M=1)")
figure(2);
plot(time,s,'r','linewidth',2);
xlabel('time(s)');ylabel('s');
title("切换函数变化曲线(M=1)")
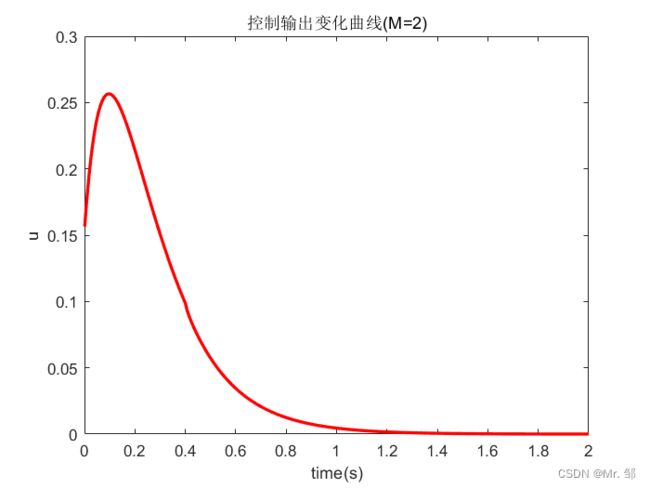
figure(3);
plot(time,u,'r','linewidth',2);
xlabel('time(s)');ylabel('u');
title("控制输出变化曲线(M=1)")
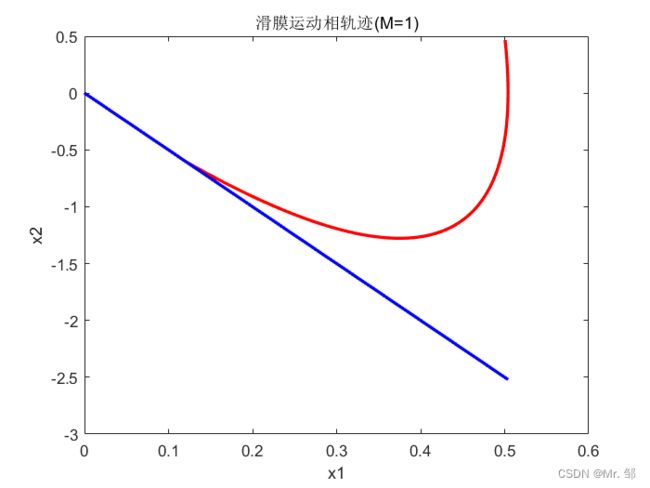
figure(4);
plot(x1,x2,'r',x1,-c*x1,'b','linewidth',2);
xlabel('x1');ylabel('x2');
title("滑膜运动相轨迹(M=1)")

3.1出图结果

 

 

 

 可以看到使用饱和函数能够抑制控制输出的抖动。

4.S函数仿真分析

4.1控制器设计

以二阶系统为例推导基于指数趋近率的滑膜控制律：

 所以控制律为：

注意：线性外推的方法预测指令信号r(k+1)和指令变化率dr(k+1) 

​​4.2调参

对基于趋近律的离散滑模变结构控制来说,有3个参数叮调,q、ε 和 c。

①趋近速度参数q主要影响切换函数的动态过渡过程,适当调整该参数能够以空系统回滑模面的趋近速度,可以更好地改善系统动态品质。q越大,系统到达滑模面的速度越快,尤其是q越接近于1/T时,系统趋近速度最快。

②对于切换函数的设计,主要是设计滑模面参数c(即滑模面斜率),其目的是保证滑模运动渐近稳定且具有较快的动态响应速度。调节该参数对系统调节时间有较大的影响,滑模面参数c越大,滑模运动段响应越快,快速性越好。因而,增大c和q都可以相应提高系统的快速性。但是参数过大会导致控制量输出过大,并且在实际控制中,往往会引起系统的抖动。

③符号函数的增益参数ε 是系统克服摄动及外干扰的主要参数,ε 越大,系统克服参数摄动和外干扰的能力就越强。但是,过大的增益将会导致系统抖振的加大,一般而言,系统的抖振幅度与ε 成正比。

4.3s函数编写被控对象

转知乎了................................

​​​​​​离散滑膜控制 - 知乎

1.二阶离散系统

一般二阶：

其中

设跟踪/指令信号为r(k)，其变化率为dr(k)，取R(k) = [r(k);dr(k)]，R(k+1) = [r(k+1);dr(k+1)]。

那么怎么通过指令信号及其变化率得到下一次的指令信号和指令变化率呢？

采用线性外推的方法预测r(k+1)和dr(k+1)，即:

具体例子：

2.控制器设计

同连续滑膜，"三部曲"+Lyapunov函数证明闭环系统稳定性：

2.1取滑膜函数

所以滑膜导函数为：

2.2选择趋近律

这里选择常用的指数趋近律，先解释下连续滑膜趋近律离散的方法，连续滑膜趋近律为:

对应离散趋近律为：

所以， ,其中T为采样时间间隔。

2.3求解控制律

有两种方法，一种是直接滑膜导函数和趋近律联立；另一种是先求等效控制项，再求鲁棒项。下面我一 一介绍用这两种方法求解：

法一

联立滑膜导函数和趋近律，得: 解出滑膜控制力：

法二

假设理想滑膜动态存在，所以s(k+1) = 0，即：

解出滑膜控制律等效项：

选取指数趋近律，所以鲁棒项：

所以，滑膜控制律为：

3.MATLAB/Simulink仿真

仿真也有两种方法，一种是利用MATLAB的m语言，第二种是利用Simulink建模结合s函数，下面也将一 一介绍。

3.1m语言仿真

首先，这里需要将连续传递函数离散化(即s域)，可以离散化为离散传递函数或者离散状态空间表达式(即z域)，离散为传递函数用默认方法是唯一的，定义采样时间为0.001s，代码如下：

G = tf([133],[1 25 0]); P = c2d(G,0.001);%将连续传递函数离散化

输出结果：

P =

6.595e-05 z + 6.54e-05

----------------------

z^2 - 1.975 z + 0.9753

离散为状态空间表达式：

有几种思路，首先离散为离散传递函数，在转化为离散状态空间表达式；或者连续传递函数先转化为连续状态空间表达式，再离散化为离散状态空间表达式。

思路一：

G = tf([133],[1 25 0]); P = c2d(G,0.001);%将连续传递函数离散化 [num,den] = tfdata(P,'v');%从离散化后的传递函数中提取出分子分母 [A,B,C,D] = tf2ss(num,den)%将传递函数转化为状态空间方程 [num,den] = ss2tf(A,B,C,D);%验证结果 sys = tf(num,den)

离散化结果：

A =

1.9753 -0.9753

1.0000 0

B =

1

0

C =

1.0e-04 *

0.6595 0.6540

D =

0

验证的输出结果：

sys =

6.595e-05 s + 6.54e-05

----------------------

s^2 - 1.975 s + 0.9753

可以看到和离散传递函数方法的结果一致。

思路二：

ts = 0.001 [A1,B1,C1,D1] = tf2ss([133],[1 25 0]) [A,B,C,D]=c2dm(A1,B1,C1,D1,ts,'z'); [num,den] = ss2tf(A,B,C,D) sys = tf(num,den)

离散化结果：

A =

0.9753 0

0.0010 1.0000

B =

1.0e-03 *

0.9876

0.0005

C =

0 133

D =

0

验证的输出结果：

sys =

6.595e-05 s + 6.54e-05

----------------------

s^2 - 1.975 s + 0.9753

可以看到和离散传递函数方法的结果一致。

思路三：是刘老师书中的，他是先自己写出连续的状态空间表达式，再进行离散化：

a=25;b=133; ts=0.001; A1=[0,1;0,-a]; B1=[0;b]; C1=[1,0]; D1=0; [A,B,C,D]=c2dm(A1,B1,C1,D1,ts,'z'); [num,den] = ss2tf(A,B,C,D)%验证结果 sys = tf(num,den)

离散化结果：

A =

1.0000 0.0010

0 0.9753

B =

0.0001

0.1314

C =

1 0

D =

0

验证的输出结果：

sys =

6.595e-05 s + 6.54e-05

----------------------

s^2 - 1.975 s + 0.9753

注：可以看到三种离散化得到的状态空间方程都不一样(可能状态空间的表达形式有很多种)，但是系统是一样的，因为验证的结果和离散传递函数方法的结果一致，但是还原的时候系统自动把其当作为连续传递函数(s域)，我也没搞懂。

好吧，以刘老师的离散化结果进行仿真，有时间再验证其他的离散化结果。

%离散化的2个方法思路： % G = tf([133],[1 25 0]); % P = c2d(G,0.001);%将连续传递函数离散化 % [num,den] = tfdata(P,'v');%从离散化后的传递函数中提取出分子分母 % [A,B,C,D] = tf2ss(num,den)%将传递函数转化为状态空间方程 % [num,den] = ss2tf(A,B,C,D);%验证结果 % sys = tf(num,den) % % ts = 0.001 % [A1,B1,C1,D1] = tf2ss([133],[1 25 0]) % [A,B,C,D]=c2dm(A1,B1,C1,D1,ts,'z'); % [num,den] = ss2tf(A,B,C,D) % sys = tf(num,den) % sy = d2c(sys) clear all; close all; a=25;b=133; T=0.001;%采样时间 A1=[0,1;0,-a]; B1=[0;b]; C1=[1,0]; D1=0; [A,B,C,D]=c2dm(A1,B1,C1,D1,T,'z'); x = [-0.5;-0.5];%x(1)状态初值 r_1 = 0;%r(0) r_2 = 0;%假设r(-1) = 0 for kk = 1:1:2000 t(kk) = kk*T;%记录仿真时间 r(kk) = 0.5*sin(6*pi*t(kk));%位置指令 %%%%%%外推法预测下一次的指令、指令变化率%%%%%%%%% dr(kk) = (r(kk)-r_1)/T; dr_1 = (r_1-r_2)/T;%dr(0) r1(kk) = 2*r(kk)-r_1;%r(kk+1) dr1(kk) = 2*dr(kk)-dr_1;%dr(kk+1) R = [r(kk);dr(kk)];%R(kk)，且R是数组，所以不能R(kk) = [r(kk);dr(kk)]，否则会当成索引，同理R(kk+1)、E(kk)、x(kk+1) R1 = [r1(kk);dr1(kk)];%R(kk+1) E = R-x;%E(kk) = R(kk)-x(kk),所以E(1) = e;E(1) = de; e(kk) = E(1);%存储误差 de(kk) = E(2);%存储误差变化率 epsilon = 5;k = 30; c = 10;G = [c,1];%滑膜面系数 s(kk) = G*E;%滑膜面 u(kk) = inv(G*B)*(G*R1-G*A*x-(T*(-epsilon*sign(s(kk))-k*s(kk))+s(kk))); x = A*x+B*u(kk);%x(k+1) y1(kk) = x(1);%x1 = x(1) = x，输出状态变量 y2(kk) = x(2);%x2 = dx(1) = dx r_2 = r_1;%更新位置指令的初值 r_1 = r(kk); end figure(1); subplot(211); plot(t,r,'r',t,y1,'k','linewidth',1); xlabel('Time(second)');ylabel('(r and x1)'); legend('ideal position signal','position tracking'); subplot(212); plot(t,dr,'r',t,y2,'k','linewidth',1); xlabel('Time(second)');ylabel('(dr and x2)'); legend('ideal speed signal','speed tracking'); figure(3); plot(e,de,'r',e,-c*e,'k','linewidth',1); xlabel('e');ylabel('de'); figure(4); plot(t,u,'r','linewidth',1); xlabel('Time(second)');ylabel('control input,u');

仿真结果：

​

编辑切换为居中

位置及速度指令跟踪

​

编辑切换为居中

控制输入

​

编辑切换为居中

相轨迹图

3.2simulink仿真

s函数编写被控对象

s函数编写控制器

未完待续......

4.4s函数编写控制器

4.5仿真结果

如果有帮助，麻烦帮忙点个赞是我最大的分享动力，非常感谢！

注：仅为便利自己学习，错误在所难免，如有侵权，请联系删除，有兴趣的学者可以参考学习交流，谢谢！

参考资料：

《滑模变结构控制MATLAB仿真：基本理论与设计方法第四版》---刘金琨