牛客网算法八股刷题系列(九)训练过程损失函数不下降问题
牛客网算法八股刷题系列——训练过程损失函数不下降问题
- 题目描述
- 正确答案: D \mathcal D D
- 题目解析
- 延伸:训练过程损失函数不下降的其他情况
题目描述
在训练神经网络时,损失函数 ( Loss ) (\text{Loss}) (Loss)在最初的几个 Epoch \text{Epoch} Epoch时没有下降,可能的原因是:
A \mathcal A \quad A学习率 ( Learning Rate ) (\text{Learning Rate}) (Learning Rate)太低
B \mathcal B \quad B正则参数 λ \lambda λ太高
C \mathcal C \quad C陷入局部极小值
D \mathcal D \quad D以上都有可能
正确答案: D \mathcal D D
题目解析
根据题干中的描述,默认的是梯度下降法,并且是训练过程中,损失函数不下降。
关于 A \mathcal A \quad A 选项,从学习率角度观察该问题时,主要原因是:在某神经元中各权重分量取值范围不平衡 的情况下,权重初始位置处于一个平滑 ( Flat ) (\text{Flat}) (Flat)范围。当学习率较小时,我们在训练初期可能无法快速找到正确的梯度方向。如下图所示的 r 2 r_2 r2初始化位置:

针对这种情况的发生,我们自然想要增大学习率,使得平滑位置的初始化权重能够快速收敛至最优解区域(红色范围)。但实际上初始化权重的位置在权重空间中的任意位置都有可能。因此我们需要:
- 手动调整学习率,从而选择一个合适的初始学习率;
- 当损失函数收敛稳定的时候,再减小学习率,使其能够找到更好的最优点。
2023/4/18 补充:这种逐步减小学习率的学习率调整方法,其效果是什么样的 ? ? ?
这里引用论文 Deep Residual Learning for Image Recognition \text{Deep Residual Learning for Image Recognition} Deep Residual Learning for Image Recognition中的图:
论文路径见下方链接。
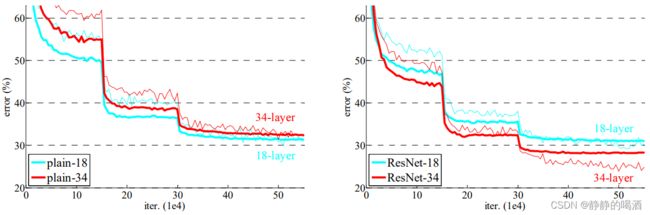
这里并不需要知道模型表达的是什么意思,仅需要知道在误差率 ( Error ) (\text{Error}) (Error)下降过程中存在一系列明显的波折——误差率并没有按照之前的拟合路线继续执行,而是突然下降。这实际上就是在迭代过程中减小了学习率(对学习率进行更细致的调整),使其摆脱当前迭代过程中震荡的约束,从而向更准确的梯度方向收敛。
因此, A \mathcal A \quad A 选项正确。
关于 B \mathcal B \quad B 选项,我们在正则化——拉格朗日乘数法中介绍过,其目标函数 L ( W , λ ) \mathcal L(\mathcal W,\lambda) L(W,λ)可表示为如下形式:
L ( W , λ ) = J ( W ) + λ ∣ ∣ W ∣ ∣ 2 − λ ⋅ C \begin{aligned} \mathcal L(\mathcal W,\lambda) = \mathcal J(\mathcal W) + \lambda||\mathcal W||_2 - \lambda \cdot \mathcal C \end{aligned} L(W,λ)=J(W)+λ∣∣W∣∣2−λ⋅C
- 其中 J ( W ) + λ ∣ ∣ W ∣ ∣ 2 \mathcal J(\mathcal W) + \lambda ||\mathcal W||_2 J(W)+λ∣∣W∣∣2使我们常见的基于 L 2 L_2 L2正则化的损失函数表达形式, λ \lambda λ是一个大于 0 0 0的常数;
- C \mathcal C C表示 L 2 L_2 L2范数在权重空间中描述的正则化范围的半径,也是一个常数。
因而 λ ⋅ C \lambda \cdot \mathcal C λ⋅C并不影响权重 W \mathcal W W的梯度。也就是说, λ ⋅ C \lambda \cdot \mathcal C λ⋅C和 W \mathcal W W的梯度方向无关。但在梯度下降法中,其目的是在每次迭代过程中找到一个与最优梯度大小相等、方向相反的向量,因而 λ ⋅ C \lambda \cdot \mathcal C λ⋅C的作用是调整该数值,使得梯度向量大小与最优梯度大小相等。
这意味着, λ ⋅ C \lambda \cdot \mathcal C λ⋅C被约束——用于调整反向的梯度向量大小:
- 当 λ \lambda λ数值较大时,由于 λ ⋅ C \lambda \cdot \mathcal C λ⋅C被约束,则 C \mathcal C C值较小。 C \mathcal C C值小意味着 L L L范数在权重空间描述的正则化范围小。即便是在正则化范围内逐步找到了最优权重,但该结果依然与最优权重相差较大:

观察上图,当 λ 1 > λ 2 \lambda_1 >\lambda_2 λ1>λ2时,对应的正则化范围半径 C 1 < C 2 \mathcal C_1 < \mathcal C_2 C1<C2,对应的正则化范围越小。
- 其中红色点表示 C 1 \mathcal C_1 C1对应正则化范围在 J ( W ) \mathcal J(\mathcal W) J(W)上的最优值;
- 同理,橙色点表示 C 2 \mathcal C_2 C2对应正则化范围在 J ( W ) \mathcal J(\mathcal W) J(W)上的最优值。
很明显,橙色点比红色点更接近 J ( W ) \mathcal J(\mathcal W) J(W)的最优解区域(红色椭圆区域)。对应在损失函数上,橙色点的损失函数下降过程会更明显。而红色点相比之下下降缓慢甚至停止下降。这同样也是欠拟合( Under-Fitting \text{Under-Fitting} Under-Fitting)的表现。 B \mathcal B \quad B 选项正确。
关于 C \mathcal C\quad C 选项,它可看做是 A \mathcal A\quad A 选项中的一种特殊情况。当 J ( W ) \mathcal J(\mathcal W) J(W)比较复杂的情况下,可能存在若干个极值点:
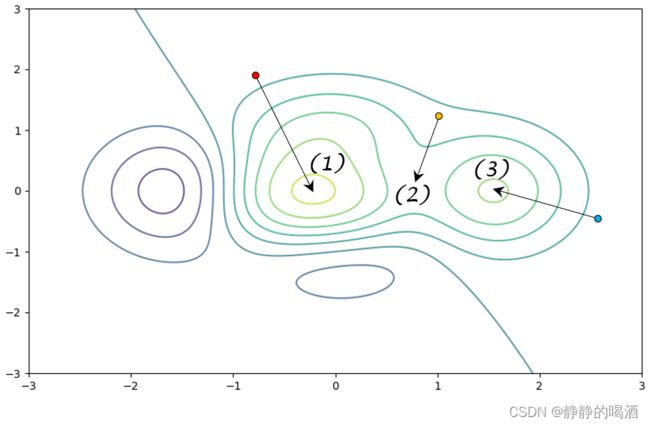
其中 ( 1 ) (1) (1)表示全局极小解区域; ( 2 ) (2) (2)表示鞍点; ( 3 ) (3) (3)表示局部极小解区域。红色点的优化路径表示期望状态下的优化路径;相比之下,橙色点与蓝色点都会使模型学习结果不准确。
如果在 ( 2 ) , ( 3 ) (2),(3) (2),(3)解区域附近生成的初始权重位置,使他们更容易进入 ( 2 ) , ( 3 ) (2),(3) (2),(3)解区域并在后续迭代过程中较难跳出,最终会产生损失函数在训练初期较难下降的情况。因此 C \mathcal C\quad C 选项正确。
综合 A B C \mathcal A\quad \mathcal B\quad \mathcal C\quad ABC 三个选项均有可能发生,因此选择 D \mathcal D \quad D 选项。
延伸:训练过程损失函数不下降的其他情况
上述选项分别从正则化、学习率、权重初始位置三个角度描述了损失函数不下降的情况。
我们在 B \mathcal B \quad B 选项中提到了欠拟合。引起欠拟合的原因还包含:
-
模型结构问题。当模型设计较简单——隐藏层、神经元少时,这可能导致模型拟合数据能力不足,具体做法是提升模型的复杂度。
-
权重初始化方式问题。不同的权重初始化方式会影响权重初始位置。常见的初始化方法有:零初始化、均匀分布、高斯分布等。
-
特征选择问题。其中一个方向是特征选择不合理,导致数据集内包含无效特征,从而增加神经网络的学习难度;具体做法是剔除无效特征。
另一个方向是样本特征过于简单、信息量不足,即便模型学习了该特征,也无法得到期望的预测结果。具体做法是考虑加入特征组合、高次特征来丰富样本的特征空间,并且高次特征能够增加模型对于高次项的调动,从而提升模型的复杂度。
详见正则化——权重衰减角度泰勒公式部分。 -
激活函数的选择问题。在神经网络学习过程中,可能出现饱和区间问题——输出特征大量存在与激活函数的饱和区间中,导致权重信息梯度消失,最终导致模型提前拟合。具体做法是调整合适的激活函数。如 ReLU \text{ReLU} ReLU。以及批标准化( Batch Normalization \text{Batch Normalization} Batch Normalization),残差网络 ( ResNet ) (\text{ResNet}) (ResNet)等等。
挖坑,关于‘残差网络’在后续进行介绍。
除此之外,关于数据集 Batch \text{Batch} Batch划分问题。如果 BatchSize \text{BatchSize} BatchSize划分过小,会导致各 Batch \text{Batch} Batch内的样本子集分布之间差异较大,从而在模型学习过程中损失函数波动较大,难以收敛(有益的影响:轻易不会陷入局部极小值/鞍点);
挖坑,后续介绍 BatchSize \text{BatchSize} BatchSize的划分问题。
如果 BatchSize \text{BatchSize} BatchSize划分过大,先不管内存问题,梯度下降的随机性减小了,首先导致收敛速度降低;其次,容易陷入极小值/鞍点。
相关参考:
loss非常大一直不下降,val_loss几十徘徊是为什么?
Deep Residual Learning for Image Recognition \text{Deep Residual Learning for Image Recognition} Deep Residual Learning for Image Recognition