Heap堆的升序排序

在heap堆中，大根堆是一种特殊的堆，它满足下列性质：对于任意一个非叶子节点i，其左右子节点的值均小于等于它本身的值。

在大根堆中，堆顶元素永远是值最大的元素，所以将堆顶元素不断取出来，就相当于对数组进行了从大到小的排序操作。

相比较于其他排序算法，使用大根堆进行数组排序的优点在于：

1：时间复杂度稳定为O(nlogn)，空间复杂度仅为O(1)，并且算法实现简洁、易于理解。

2：由于大根堆的特殊性质，堆排序还具有良好的局部性和稳定性，能够保持元素在排序前后的相对位置关系，不会改变具有相同值的元素之间的顺序。

下面用图片来梳理我们的思路

---

                                        代码注解

首先我们先创建一个数组：

1： 首先我们将数组中的值建立成大根堆

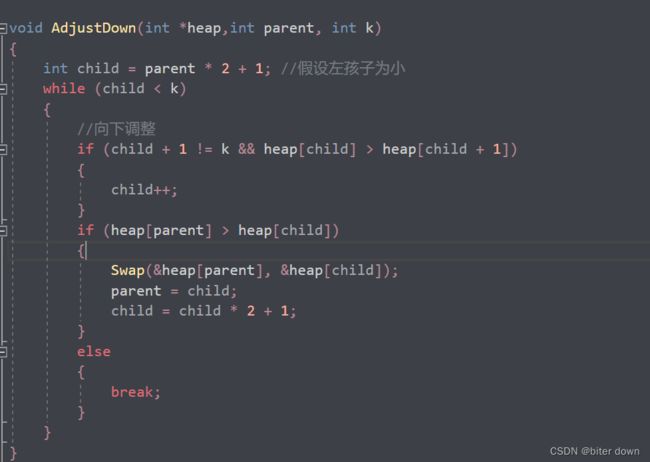
2：首尾换位，向下调整成为循环

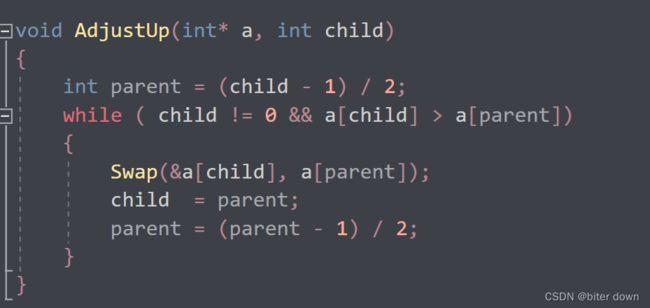
 我们将数组中的值建立成大根堆的Adjustup函数的实现

Adjustup函数的实现的空间复杂度(3条消息) 堆的向下调整与向上调整的时间复杂度_biter down的博客-CSDN博客

我们将数组中的值建立成大根堆的Adjustup函数的实现

Adjustdown函数的实现的空间复杂度(3条消息) 堆的向下调整与向上调整的时间复杂度_biter down的博客-CSDN博客

 

---

                                   源码提供参考：

#include
void Swap(int* p1, int* p2) {
    int t = *p1;
    *p1 = *p2;
    *p2 = t;
}

void AdjustDown(int* a, int size) {
    int parent = 0;
    //将leftchild作为最大的孩子
    int child = parent * 2 + 1;
    while (child < size)
    {
        //当leftchild的值小于rightchlid时，child的值应该为较大值的右孩子
        if (child + 1 < size && a[child + 1] > a[child])
        {
            child++;
        }
        Swap(&a[child], a[parent]);
        parent = child;
        child = child * 2 + 1;
    }
}

void AdjustUp(int* a, int child)
{
    int parent = (child - 1) / 2;
    while ( child != 0 && a[child] > a[parent])
    {
        Swap(&a[child], a[parent]);
        child  = parent;
        parent = (parent - 1) / 2;
    }
}

//排升序，建大根堆
void HeapSort(int* a,int n)
{
    //将数组中的值建立成大根堆
    for (int i = 1; i < n; ++i)
    {
        AdjustUp(a, i);
    }
    //将大根堆数组的元素升序
    for(int i=n;i>0;i--)
    {
        Swap(&a[0], &a[i]); //首尾互换
        AdjustDown(a, i); //向下调整
    }
}
int main()
{
    int arr[10] = { 2,1,5,7,6,8,0,9,4 };         //对数组进行大根堆排序
    HeapSort(arr, sizeof(arr) / sizeof(arr[0])); 
    return 0;
}