【数据库】— 无损连接、Chase算法、保持函数依赖

Chase算法

形式化定义：

• 构造一个$k$行$n$列的表格，每行对应一个模式$Ri(1\le i\le k)$，每列对应一个属性$Aj（1\le j\le n）$，若$Aj$在$Ri$中，则在表格的第$i$行第$j$列处填上$aj$，否则填上符号$bij$
• 检查$F$的每个$FD$，并修改表格中的元素，方法如下：
  • 对于F中的函数依赖$X\to Y$，若表格中有两行在$X$分量上相等，在$Y$分量
    上不相等，则修改$Y$：
    • 若$Y$的分量中有一个$aj$，则另一个也修改为$aj$；
    • 如果没有$aj$，则用其中一个$bij$替换另一个符号（$i$是所有$b$中最小的行数） ，一直到表格不能修改为止
• 若修改后，表格中有一行是全$a$，即$a1a2\dots an$，则$p$相对于$F$是无损连接的分解，否则不是
  举例：

$$\begin{gathered} 关系模式：R(A,B,C,D,E) \\ 分解：R1(A,D),R2(A,B),R3(B,E),R4(C,D,E),R5(A,E) \\ 函数依赖：F=\{A\to C,B\to C,C\to D,DE\to C,CE\to A\} \\ 判断R分解为p＝R1,R2,R3,R4,R5是否是无损连接的分解 \end{gathered}$$

Chase算法举例

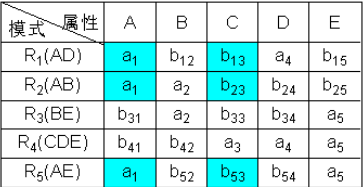
① 构造一个初始的二维表若“属性”属于“模式”中的属性，则填aj，否则填bij

② 根据A→C，对上表进行处理，由于属性列A上第1、2、5行相同均为a1，所以将属性列C上的b13、b23、b53改为同一个符号b13（取行号最小值）。

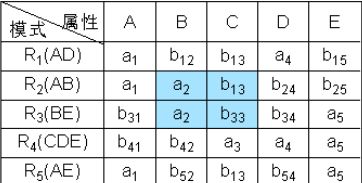
③ 根据B→C，对上表进行处理，由于属性列B上第2、3行相同均为a2，所以将属性列C上的b13、b33改为同一个符号b13（取行号最小值）。

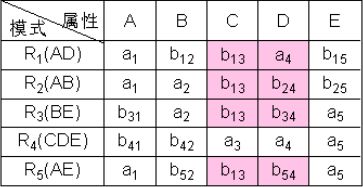
④ 根据C→D，对上表进行处理，由于属性列C上第1、2、3、5行相同均为b13，所以将属性列D上的值均改为同一个符号a4。

⑤ 根据DE→C，对上表进行处理，由于属性列DE上第3、4、5行相同均为a4a5，所以将属性列C上的值均改为同一个符号a3。

⑥ 根据CE→A，对上表进行处理，由于属性列CE上第3、4、5行相同均为a3a5，所以将属性列A上的值均改为同一个符号a1。

⑦ 通过上述的修改，使第三行成为$a1a2a3a4a5$，则算法终止。且分解具有无损连接性。

Chase算法示例部分参考链接

一种简便方法：分解为两个模式时

无损连接和函数依赖的一个简单例子