概率密度函数的参数估计

---

前言

写作参考概率论书籍、西瓜书、李航《统计学习方法》及其他资料，若有不足请大家不吝赐教！

---

一、文章重点及流程梳理

本文目的在于：
1、阐述MLE参数估计的思想，并计算参数在正态分布下的估计量
2、阐述贝叶斯估计的思想，并介绍贝叶斯估计与MAP的不同点

流程梳理：
1、介绍这部分所涉及的概率论知识，包括条件概率、全概率、事件独立性、贝叶斯公式。
2、介绍MLE并求解参数在正态分布下的估计量，并进行比较。
3、介绍贝叶斯估计及MAP的思想。

二、概率论基础知识

1.条件概率
$$P\left(B|A\right)=\frac{P\left(AB\right)}{P\left(A\right)}\left(1\right)$$

通过下图对上式进行描述：
图中有两集合A、B，黄色部分为A、B的交集部分。则P(B|A)表示在A发生的情况下，B发生的概率，可以通过交集部分发生概率占A所发生概率的比值表示。同理，若要求P(A|B)只需要换成交集部分发生概率占B所发生概率的比值。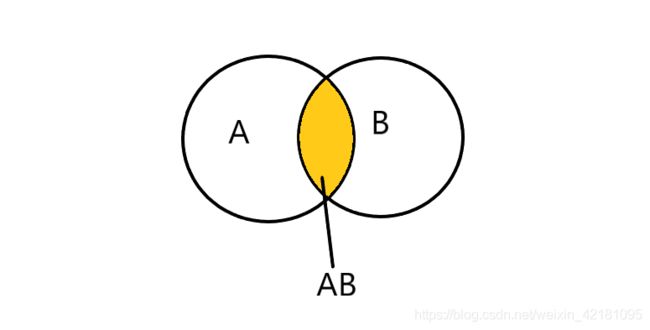

2.事件独立性
定义：在一次试验中，一事件发生与否与另一事件是否发生无关。满足下式：
$$P\left(AB\right)=P\left(A\right)P\left(B\right)\left(2\right)$$

则称A、B相互独立。

PS:独立同分布指的是随机变量服从同一分布且相互独立。

3.全概率公式
$$P\left(A\right)=\sum _{i=1}^{n}P\left(B_i\right)P\left(A|B_i\right)\left(3\right)$$

公式解读：若A事件的发生可由多项B事件引起，那么这时候A发生的概率等于B事件发生的概率乘以B事件发生条件下A发生概率之和。

举个栗子：假设A是今天感到快乐的概率，可以通过吃东西B1，或者是买了新衣服B2，或者是出了考试成绩B3，或者是有人和自己告白B4。那么，所有的B事件发生，需要一定的概率；在B事件发生得概率下，开心和不开心都存在可能，而我们只取B事件下开心的概率，这时候A要发生的概率，就是所有B事件发生概率*B事件下A发生得概率的和。

4.贝叶斯公式（逆概公式）
贝叶斯公式的初始形式：
$$P\left(B|A\right)=\frac{P\left(A|B\right)P\left(B\right)}{P\left(A\right)}$$
其中，P(A|B)称为似然（likelihood），P(B)称为先验（prior），P(A)称为事实，P(B|A)称为后验（posterior）。

后验P(B|A)求的是在A发生条件下，B发生得概率；似然P(A|B)求的是，若A发生则B作为影响因子出现的概率。

通过式（1）和式（2），可得到如下贝叶斯公式的变形：
$$P\left(B_j|A\right)=P\left(B_j\right)\cdot \frac{P\left(A|B_j\right)}{{\sum }_{i=1}^{n}P\left(B_i\right)P\left(A|B_i\right)}\left(4\right)$$
通过下图对上式进行理解：

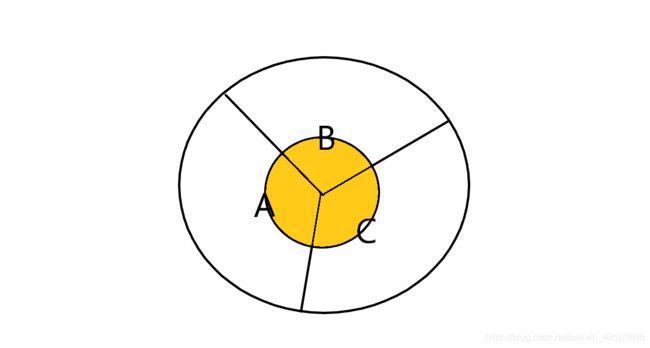
整个圆划分为三个部分A、B、C，黄色部分为M集合，若此时求M发生A中的概率，则
$$P\left(A|M\right)=\frac{P\left(A\cap M\right)}{P\left(M\right)}$$

$$=\frac{P\left(M|A\right)P\left(A\right)}{P\left(M|A\right)PA+P\left(M|B\right)P\left(B\right)+P\left(M|C\right)P\left(C\right)}$$

通过例子可知，后验概率目的在于，已知M发生后，想知道由A引发M事件的概率，即为：知道结果后反推原因。

三、参数估计

1.极大似然估计（Maximum Likelihood Estimation）

1、MLE思想

频率派角度：认为参数是固有的，但是可能由于一些外界的噪声干扰，使数据看起来不是完全由参数决定。但只要在这个数据给定的情况下，找到一个概率最大的参数就可以了。即，模型已定，参数未定。
$$P\left(x|\theta \right)$$

2、MLE表示形式
当存在多个样本时，需要多个似然相乘，此时样本间独立同分布，即：
$$P\left(D_c|{\theta }_c\right)=\prod _{x\in D_c}P\left(x|{\theta }_c\right)$$
对式子取对数得到：
$$LL\left({\theta }_c\right)=\sum _{x\in D_c}\log P\left(x|{\theta }_c\right)$$
则可以得到极大似然估计的表达式：
$$MLE=arg\underset{{\theta }_c}{\max }P\left(D_c|{\theta }_c\right)=arg\underset{{\theta }_c}{\max }LL\left({\theta }_c\right)$$试图在θ的所有取值中，找到一个使式子最大化的θ。

3、求解极值

假设参数θ满足正态分布，即 θ =（μ，∑），在一维情况下，θ =（μ，∑^2）
则有：$$MLE=arg\underset{{\theta }_c}{\max }\sum _{i=1}^{N}P\left(x_i|\theta \right)=arg\underset{{\theta }_c}{\max }\sum _{i=1}^N\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{{\left(x_i-\mu \right)}^2}{2{\sigma }^2}}$$

此时，问题转换成了求参数θ的MLE。

• step 1：求μ的极值
  $$\begin{gathered} \frac{\partial \mu }{\partial \theta }={\left(-\sum _{i=1}^N\cdot \frac{1}{2}\log 2\pi -\sum _{i=1}^N\log \sigma -\sum _{i=1}^N\frac{{\left(x_i-\mu \right)}^2}{2{\sigma }^2}\right)}_{\mu }^{\prime } \\ =\sum _{i=1}^N\frac{2\left(x_i-\mu \right)}{2{\sigma }^2} \end{gathered}$$

令上式取0，得：
$$\sum _{i=1}^N{x}_i=\sum _{i=1}^N\mu ⟹{\mu }_{MLE}=\frac{1}{N}\sum _{i=1}^N{x}_i$$

• step 2：求δ的极值
  $$\begin{gathered} \frac{\partial \sigma }{\partial \theta }={\left(-\sum _{i=1}^N\cdot \frac{1}{2}\log 2\pi -\sum _{i=1}^N\log \sigma -\sum _{i=1}^N\frac{{\left(x_i-\mu \right)}^2}{2{\sigma }^2}\right)}_{\sigma }^{\prime } \\ =-\sum _{i=1}^N\frac{1}{\sigma }+\sum _{i=1}^N\frac{{\left(x_i-\mu \right)}^2}{{\sigma }^3} \end{gathered}$$

上式取0，得：
$$\sum _{i=1}^N\frac{1}{\sigma }=\sum _{i=1}^N\frac{{\left(x_i-\mu \right)}^2}{{\sigma }^3}⟹{\sigma }_{MLE}^2=\frac{1}{N}\sum _{i=1}^N{\left(x_i-{\mu }_{MLE}\right)}^2$$

4、MLE估计结果
判断在参数为正态分布的情况下，所得到的估计与实际是否一致。
$$E\left({\mu }_{MLE}\right)=\frac{1}{N}\sum _{i=1}^{N}E\left(x_i\right)=\frac{1}{N}\sum _{i=1}^N\cdot \mu =\mu$$

对所得的均值求期望，得到的结果为，正态分布下的均值为样本均值，与正太分布下的均值相同，为无偏估计。

对所得的方差求期望，得到的结果为，正态分布下的方差为原方差的N-1/N倍，比原方差小，为有偏估计。

由上可知，在参数服从正态分布的条件下，若要方差为无偏估计，则需要除以这个偏差，可得：
$${\sigma }^2=\frac{N}{N-1}{\sigma }_{MLE}^2=\frac{N}{N-1}\cdot \frac{1}{N}\cdot \sum _{i=1}^N{\left(x_i-{\mu }_{MLE}\right)}^2=\frac{1}{N-1}\cdot \sum _{i=1}^N{\left(x_i-{\mu }_{MLE}\right)}^2$$

5、Q & A
Q（1）：为何参数要服从正态分布？其他分布呢？
Q（2）：参数正态分布下的MLE为何方差有偏差？

A（1）：可以使用其他分布，如伯努利分布、二项分布、均匀分布等，但在正态分布下有偏的程度最小。

A（2）：此时，在求方差时，是以MLE下的均值μMLE代替均值，而此时的μMLE为样本均值，而期望是总体均值，在随机取值的情况下，取到的μMLE偏大的可能性大，所以此时所求的方差会比原方差小。大数定律下，样本均值可以等于总体均值。

2.贝叶斯估计

由上一节可得到基于MLE的参数估计方法，但是该方法本身依赖于所假设的分布形式是否符合潜在的真实分布。即MLE只考虑了单一模型，由一个模型产生一个已知数据的概率，没有考虑模型本身的概率。

---

1、贝叶斯派思想

贝叶斯派角度：认为参数是未观察到的随机变量，其本身也可有分布，因此，可假定参数服从一个先验分布，然后基于观测到的数据来计算参数的后验分布。

2、贝叶斯估计
$$P\left(\theta |D\right)=\frac{P\left(D|\theta \right)\cdot P\left(\theta \right)}{P\left(D\right)}$$
上式表示的是贝叶斯下的参数估计。
它根据参数的先验分布p(θ)和一系列观察X，求出参数θ的后验分布p(θ|X)，然后求出θ的期望值，作为其最终值。即：通过现实样本回馈来调整先验假设中参数的概率分布。
使用贝叶斯估计来进行参数估计有以下三种：

• 使用后验分布的密度函数最大值点作为θ的点估计的最大后验估计（MAP）。
• 使用后验分布的中位数作为θ的点估计的后验中位数估计。
• 使用后验分布的均值作为θ的点估计的后验期望估计。

由于后验概率是一个条件分布，通常取后验概率的期望作为参数的估计值。
3、最大后验概率估计MAP推导过程

• step 1：期望风险函数
  记对数似然损失函数如下：$$L\left(Y,P\left(Y|X\right)\right)=-\log P\left(Y|X\right)$$
  理解：似然表示的是该参数作为影响因子导出结果的可能性，似然越大越接近真实值，那么损失函数就越小。

回顾一下求期望的方法：
假设X作为随机变量，Y=g(X)，且E(Y)存在，则有
（1）变量为离散型：
$$E\left(Y\right)=E\left[g\left(X\right)\right]=\sum _{i=1}^{\infty }g\left(x_i\right)p_i$$

（2）变量为连续型：
$$E\left(Y\right)=E\left[g\left(X\right)\right]={\int }_{-\infty }^{+\infty }g\left(x\right)f\left(x\right)dx$$

于是乎，可对上方似然损失函数进行期望求解，作为理想状态下对全局所有样本预测错误程度的均值。
$$R_{\exp }\left(f\right)=E\left[L\left(Y,P\left(Y|X\right)\right)\right]$$

若此时，假设有N中可能的类别标记，Y={c1,c2,…,cN}，将λij表示为将真实标记j误分类为i所产生的损失,且损失函数使用0-1损失函数表示分类结果，即:
$$L\left(Y,f\left(X\right)\right)=\{\begin{array}{l}1\text{，}Y\ne f\left(X\right)\\ 0\text{，}Y=f\left(X\right)\end{array}$$
得到最终的期望损失函数：
$$R_{\exp }\left(c_i|x\right)=\sum _{i=1}^N{\lambda }_{ij}P\left(c_j|x\right)$$

P(ci|x)表示的是取值为x的情况下判为cj后所带来的损失。

• step 2：转换成MAP问题
  若此时的Rexp作为误差损失，则令P(c|x)作为此时分类器所能达到的最佳性能。
  $$P\left(c|x\right)=1-R\left(c|x\right)$$
  则最小化期望风险转化为最大化后验概率：
  $$f\left(x\right)=arg\underset{c\in Y}{\max }P\left(c|x\right)$$

参考链接

贝叶斯估计