一文读懂群延时(Group Delay)：非常简单易懂

0 目的

本文用非常通俗易懂语言说明什么是群延时（Group Delay），让你在几分钟之内建立对群延时感性认识，如果你恰好对它的概念和作用比较模糊，那么这篇文章非常适合你。

这篇文章是我读一篇英文document后，根据自己的理解整理而得，文末有链接。

1 什么是群延时

本文将不使用数学公式的情况下解释什么是group delay 群延时，以及它的作用。

群延时的定义很简单：相位与频率比值的负导数。

2 为什么叫“群延时”（Group Delay）

延时（time delay）、相移（phase shift）我们都熟悉，但是什么叫群延时呢？

先说说方波，它是由一系列不同频率和相位的正弦波叠加而成。

如果让它通过一个系统（比如滤波器），要想输出还能保持方波的形状，那么不同频率的正弦波在时域上的相对位置不能发生变化，简单的说，就是需要所有频率波的delay时间一样，否则，方波的形状就要发生变化。

需要注意的是，这里的delay不是指相位滞后，而是指延时，单位就是时间。

滤波器肯定会带来延时，极点或taps越多，延时也越大。对于数字滤波器，我们一般用采样点数量而不是时间来衡量延时的大小。

3 群延时（Group Delay）与相移（Phase Shift）

一定要分清延时（time delay）和相移（phase shift）的区别。延时的单位是时间，比如秒、毫秒等，相移的单位是角度，比如弧度、度等。对于一个正弦信号，如果频率已知，那么相移和和延迟是可以换算。

延迟＝相移/频率

所以（敲黑板）：
1）延迟是一定时，频率越大，相移也越大
2）相移一定时，频率越大，延迟越小。
所以延时和相移和当前的频率有关。

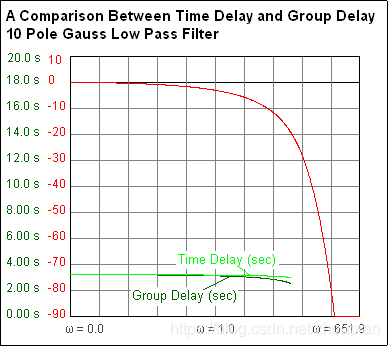
这里，我们比较低通滤波的延时（time delay）和群延时（group delay）。在带通范围内，相移线性变化（下图中没有画出相移），延时和群延时几乎相等。

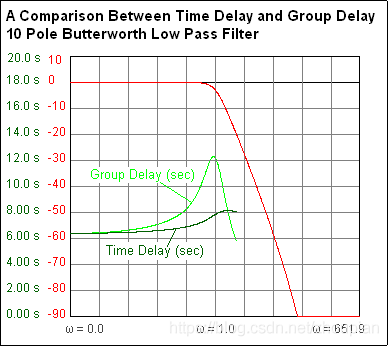
从上图可以看出，我们不能简单的把延迟和群延时画上等号。
FIR在所有频段，延迟和群延时都相等，但是对于巴特沃斯这样这样的非线性相位滤波器，它们仅在通带内接近接近相等。

下图是一个高斯滤波器，它在更宽频率范围内有线性相位。

不严格的讲，群延时可以认为是信号通过系统所需要的时间。比如信号以光速c通过长度为L的光纤（所有频率的光的传播速度相等），需要的时间是dt＝L/c，这里的dt就可以认为是群延时。

4 群延时（Group Delay）和信号传播时间（Signal Propagation Time）

不严格的讲，正如前面提到的，群延时可以理解为信号通过一个系统需要的时间。为了说明这一点，我们让一个方波通过一个低通滤波器，这个滤波器的群延时为定值40 sample，方波的上升一半幅值所需要的时间也是40 sample。

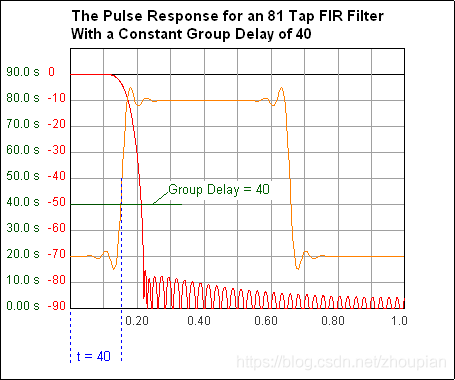
上面我们以低通滤波和方波为例对群延时进行了说明，因为方波的延时能更直观的看到。但是你必须明白，任何一种信号，不管它是正弦波还是其它，不管它的频率是多少，它通过这个低通滤波器的延时是相同的。

5 为什么使用方波（square pulse）举例

既然任何信号通过系统都会畸变，那我们为什么选择方波来考量畸变程度呢，原因有二。
1）阶跃信号包含所有的频率成分（傅里叶级数就不在这里讲了，不清楚可以另找资料学习），所以有点像扫频测试。
2）我们很容易观察到阶跃信号的畸变。

6 为什么群延时很重要？

当你在学习群延时的时候，你清楚你为什么要学习、了解它吗？
一般情况下，我们并不是很关心滤波器的延时的大小，而更在意不同频率的信号他们的延时是否相等、他们的相对相位是否不变，换句话说，我们希望一个信号通过一个系统时，它的形状不发生变化。

上面例子中的滤波有很完美的群延时特性，但是信号通过它时依然发生了畸变，信号上升沿还有超调，为啥呢？
方波信号有无限的频率的正弦信号组成，而低通滤波的主要功能就是让频率低的信号通过，频率高的信号被截止。所以方波通过低通滤波器后，只有低频被保留了，高频信号都没有了，发生畸变就很正常了。

所以造成信号的畸变有两个因素：
1）不同频率信号的相对相位关系的变化
2）不同频率信号的幅值变化

我们在本文讨论是第1个因素。有一点必需要注意：虽然群延时的曲线可以反映对信号畸变程度，但是它不是引起信号畸变唯一因素。只能说群延时为常数时，信号的畸变是最小的。

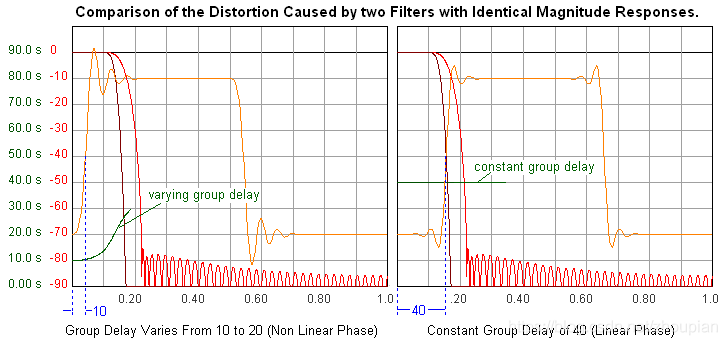
下图是两个不同截止频率但群延时相等的低通滤波器对信号畸变的影响程度对比，可以看出，截止频率低的滤波器有更严重的畸变。

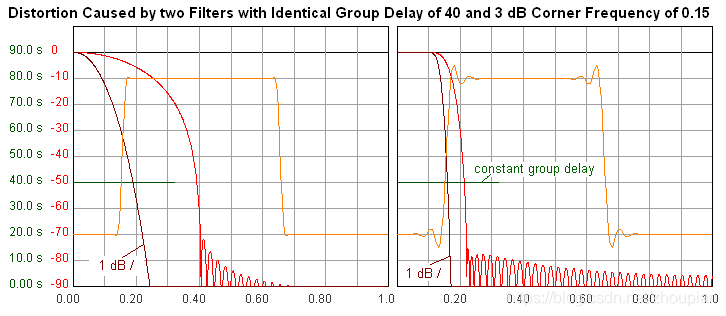
同样，我们比较一下幅频响应相同但是群延时不同的滤波器，可以很明显看到，群延时为定值的滤波器对信号的畸变更小，而群延时为变值的滤波器畸变更严重，有更明显的超调和震荡现象。

7 一个极端的例子

你或许听说过全通滤波器，你是否有这样的疑问，既然所有的频率都能通过且幅值不发生变化，为什么为什么还叫它滤波器呢？

全通滤波器的重点不是幅频特性，而是相频特性，

它可以用于对信号进行延时（相当于向后平移），以便和另一个信号对齐。
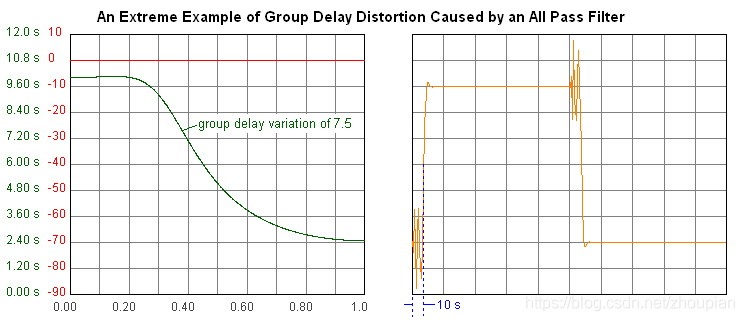
下图中是一个IIR滤波器，虽然在全频域幅值没有衰减，但是由于群延迟不是常值，所以输出的波形仍然发生了畸变，但是如果换成FIR具有常值群延时的滤波器，输出的波形就仅仅有延迟，而没有畸变。

8 群延时可以是负值（Negative）吗？

有一点必须要明确，对于一个真实的物理系统（纯数学模式除外），它的群延时不可能是负值，否则意味着信号还没有进入系统就已经有输出了。

然而，我们可以设计一个具有负群延时的有源电路（不是无源电路）。只需要把系统的极点放置在虚轴的右侧，电路会处于不稳定状态，会在极点对应的频率发生震荡，如果恰好你想设计一个震荡器，就正合你意，但其实我们一般不这么干。

这里通过一些简单的叙述和例子对群延时进行了说明，虽然它并不复杂，但是要真正了解它的含义，还需要在工程实践中多多体会。

9 参考

http://www.iowahills.com/B1GroupDelay.html