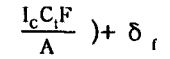供水管网爆管预测模型研究现状
配水管网是供水系统中最昂贵的组成部分。管网运行管理和调度技术难度高,爆管事故 容易发生,对人民生活、工业生产、城市交通及社会安定造成不利影响,造成严重的经济损 失。合理的管道的修复更新计划是满足供水目标、实现对管网的科学管理的重要环节。以管道状态密切相关的管道爆管次数为评价指标,了解和量化管道损坏的机理,找出影 响爆管的主要因素及其相互作用关系,建立爆管的预测模型,对管网的现状进行评价,对未 来做出预测,是建立管网维护管理的决策系统的有效手段。爆管预测模型可以分为两大类:第一类物理模型,第二类是统计模型。
1.物理模型
爆管预测的物理模型是试图分析作用在管道上的荷载、管道抗荷载的能力、管道内外所 受腐蚀的程度、范围来预测管道事故。导致爆管的物理机理极其复杂,有些情况尚无法完全 解释清楚。这些物理机理包括以下三个主要的方面:(1)管道结构特性、管道材料类型、管 道与土壤的相互作用、管道安装质量;(2)管道内部水流的压力和管道外部荷载的大小。外 部的荷载包括:土壤荷载、车辆荷载、冰冻造成的荷载和第三方的影响等等;(3)由于发生 在管道内外的化学反应、生物反应和电化学反应造成的对管道材料的腐蚀。
物理模型分成单因素物理模型、确定性物理模型和概率性物理模型。
1.1单因素物理模型
影响爆管的因素众多,针对其中某一个因素对管道的作用建立数学模型,如下表所示:
表1.单因素物理模型
| 模型名称 | 具体模型举例 | 模型参数说明 |
| 冰冻荷载模型 | p。是在管段上任意点s的冰冻荷载的大 小,d。是冰冻深度,i是时间步长的标号,N,是时间步长的总数,h+是总的冰冻拉力(frost heaVe),B。是沟槽宽度,K。是 冰冻线(freezing fro眦)以下弹性未冰冻 土壤的硬度,p是衰减系数,k。是回填边 墙的抗剪刚度,H是用以计算压力影响的 Bou8sjnesq函数, | |
| 管道一土壤相互作用模型 | 6。为总的平面压力,c。、c。分别是土壤 荷载和表面荷载系数,k。是挠矩系数,E。是管道弹性模量,P.是管道内部压力,r和t分别是管道的直径和管道壁的厚度,k。是由垂直荷载的分布和作用决定的偏 差系数,L是车辆作用因素,F是路面上k。是由垂直荷载的分布和作用决定的偏 差系数,L是车辆作用因素,F是路面上 | |
| 残余结构抗力(residuaIstructuraIresistance)模型 | D。是管道发生事故时的压力,d是腐蚀破坏的最大深度,A是管道径向轴上的被腐蚀金属区有代表性的腐蚀区面积,A。代表性腐蚀区域最初的面积,I是腐蚀破坏的最大长度,r是管道半径,h是管道 壁的厚度,s.,管道yieId strength,M是FoIias系数用以解释管道发生事故前受到管道 内部的压力膨胀。 | |
| 腐蚀状态指数模型 | P。。是长度为1米的管段上腐蚀坑的平均深度,t是管道壁的厚度。(假设新管道的CsI值是1 OO,若平均腐蚀深度达到最 初管壁厚度的70%,csl值为30) |
单因素物理模型的建立可以加强某个因素对爆管影响机理的理解,因此有利于找到减轻 该因素对管道的影响的途径。例如管道一土壤相互作用模型可以解释观测到的一些现象如:小管径管道每单位长度上的爆管事故较大。模型还表明土壤的温度降低可能导致环向爆管孽 故增加,为管道在寒冷季节爆管率增加提供了物理上的解释。然而这些模型很复杂,所需箱 入的参数较多,而且其有些是不易获得的。例如腐蚀状态指数模型的数据要求包括管龄、管材类型、管壁厚度、管径、土壤性质一电阻率、氯化物、硫化物、PH值、湿度、第一次爆 管年份等。冰冻荷载模型中需要的回填土的特性数据在市政工程建设中一般不常用,除非是 那些寒冷地区的工程设计者对该参数才有了解。
1.2确定性物理模型
Doleac、 Lackey和Bratton等人利用RoSSum提出的指数方程把腐蚀坑深度与管龄联 系在一起预测灰铸铁管道的剩余管壁厚度‘·1:
(1)
式中,p是平均腐蚀坑深度,a、Kn、Ka 是现场试验或实验室试验得到的经验数据,A。是管 道腐蚀的表面积,PH是指管道周边土壤的PH值,p是土壤的电阻率,n是土壤的通风常数,t是时间。
该模型存在一些缺陷,例如,没有足够的研究记录可以证明RoSsum提出的随时间变化 腐蚀坑增长状况预测模型的合理性,还有公式(1)中的参数A难以确定。该模型要求的数 据有管龄、管道周围土壤特性(电阻率、PH值、通气常数)参数是可以既方便又经济的得 到的。Rajalli和Makar建立了另一个通过考虑管道的腐蚀程度来预测灰口铸铁管的剩余服 务时间的模型。他们提出的模型综合了单因素物理模型公式及上式中所有考虑到的因素,运 用反复叠代的方法得到灰口铸铁管段的剩余服务期限。
模型需要的基础资料包括:(1)管道数据资料,如管径、管道壁厚度、安装时间、埋设 深度、管道类型;(2)土壤数据资料,如类型、密度、PH值、电阻率、通气条件;(3)安 装数据资料,如埋设状况、荷载因素、静止水平应力系数;(4)运行状况数据资料,如水压、 波动压力、冬季和夏季的水温和气温、轮压荷载、交通工具影响因素、冰冻荷载因素。为确 定模型的基本条件需要大量不同的背景数据。模型需要的数据包括材料特性、管龄、管道壁 厚、管道内外壁的腐蚀坑的深度。材料特性数据具体包括:抗张强度、断裂韧度、弹性模量、 挠曲强度等。在规模小的配水系统里依靠挖掘管道样本来检测这些数据是不经济的。非破坏 检测技术的进步将会促进该模型的使用。
1.3概率性物理模型
概率物理模型总的来说还是属于物理模型的框架,但是把概率的方法用于探求模型中不 确定参数的分布,这些不确定因素在确定性模型中是被忽略的。例如:Ahammed和Melchers【21建立的估计钢管事故概率的模型属于早先提出的力学模 型的框架。他们利用表l中管道一土壤相互作用模型作为基础力学应力模型。因为该公式中 ~ 70 — 的管道壁厚度是一个变量,他们用了一个简单的幂的模型D=atn(D是腐蚀坑的深度,a是 比例常数,t是时间,n是回归参数)。因此他们得到了平面拉应力与管龄之间的关系等式。模型中的每个参数和独立变量都假定符合已知中值和方差的概率分布。导致管道事故的物理原因分析所需的数据通常不易获得或者要花费高昂的费用获得。因 此,物理模型一般只用于大型的主干管道,因为它们一旦发生事故则影响巨大。
2.统计模型
爆管预测统计模型是以对管网运行的爆管数据记录为依据,利用统计的方法量化爆管事 故的规律。统计模型可以分成两种:确定性统计模型和概率性统计模型。
2.1确定性统计模型
爆管预测的确定性统计模型一般要利用回归分析得到,而此时回归分析法应该建立在管 道分组的基础之上,管道分组又应以影响爆管的因素为准则进行划分,比如按照管道使用的 年限进行分组。此类模型的应用是简单、直接的,而且相对容易实现,但是在使用模型时要 确保数据的被均匀的分入各组。建立该类模型的难点就在于对现有数据进行合理的分组。该 模型的表达式如表2所示。
表2.确定性统计模型
| 模型名称 | 模型名称 | 模型名称 |
| 时间指数模型 | t为从现在算起的使用年限;N(t)是每年 每单位长度爆管的次数;N(t0)是管道刚 安装那一年的爆管次数,g是到t年时的管龄,A时爆管率增长的系数(年-1)。注意N(t0)不等于0,这就意味着从平均 值上来看管道总是假定有爆裂的可能性 的,只是这种可能性在它刚刚使用时比 较小。 | |
| 时间线性模型 | N是每年的爆管次数,k。是回归系数,Age 是管段第一次爆管的管龄 |
2.2多变量概率模型
多变量的概率模型可以量化地考虑多个变量。这一特点使得该方法能较好的预测爆管 率。同时,它对数据分组的要求不高。但是,它的数学模型非常复杂而且需要足够的经验。
表3.多变量概率模型
| 模型名称 | 模型名称 | 模型参数说明 |
| 比例危险模型(Proportionalhazards models ) | t是时间;h(t,z)危险函数,表示的是 事故瞬间发生率,即假定能存活到时间t,那末在t+△t的时问上发生事故的概率;h.(t)是任意的危险函数的基线,z是作用于危险函数的多变量的向量。b 是从现有数据中用回归的方法得出的系 数向量。 | |
| 加速寿命模型(Accelerated liftime models)) | T为下次爆管事故的时间,×为解释性向量集,o预计的最大可能性参数,p为 预计的参数向量,z为Gumbel分布的随机变量。 | |
| 实时泊松(Poisson)模型 | t是管龄,H(t)是管道年龄为t时每单位长度上的平均爆管次数,e、p分别为比例和形状参数,0。为基线值,a是回归方法计算出来的参数向量,z是 影响爆管率的参数向量。 |
比例危险模型功能十分强大,原因在于它有灵活和强大的理论基础,是研究者采用较多 的模型。但是需要丰富的技术经验。对左截断数据(1eft—cenSored data)不敏感以及可 以考虑右截断数据(right—censored data)是它的优势之一。另外,建立该模型还是需要 分组,只是分组所要求的工作量较小。如果要想有好的预测效果对所使用的数据必须经过仔 细的检查,特别是对那些需要进行数据分组的情况。比例危险模型还可以用于不同的数据水 平进行预测。影响管道事故的变量数据量越多,越有利于模型的使用。当数据量足够多时, 预测就可能推广到对单独管道的事故预测的水平上来。要注意的是影响每个供水部门的管网 的变量各有不同,这主要取决于现行的环境情况、运行条件和所采用的管道类型。目前的情 况是,大多数供水部门缺乏相关数据,使得这个模型潜在的优势无法发挥出来。
加速寿命模型与比例危险模型是类似的。它们的区别来自于比例危险模型的变量是与事 故发生的时间间隔有关,事故危险性受到影响。如果加速寿命模型的Z为WeibuⅡ分布,加 速寿命模型可以转变成为比例危险模型。如果把管道以前的事故次数作为一个变量的话,会 增加应用该模型的复杂性。因为在两种模型中各种影响互相作用,而各个影响参数被认为是 以互不影响的方式作用与模型,所以需要对数据进行分组。只要数据可靠,加速寿命模型与 比例危险模型一样具有较大的通用性,但是也需要有经验的专家才可以有效的利用它们。
2.3单变量组过程概率模型(Probabilistic Single—variate group—proceSsing modelS)
该类模型把管道分成相对均匀的几组,每一组建立它们的最优更换时间,对评价配水系 统今后的经济需求是一个有用的工具。它可以对长期的管道修复预算计划提供有用的帮助。但模型只对一些大的管群有用,而不适合对个别管段制定修复计划。模型形式如下:
表4.单变量组过程概率模型
| 模型名称 | 具体模型举例 | 具体模型举例 |
| 群生存模型(Cohort surViValmodels) | t是管道的有效寿命,a是时间因子(年-1),b是事故因子(年-1),c是反抗时间(resistance time以年为单位),例如 管龄小于c年时不予更换。 | |
| 贝叶思诊断模型(Bayesiandlagnostic modeI) | ||
| 爆管历史的半爆管历史的半 | 按照爆管次数进行分级,如一次爆管,两次爆管、三次爆管等等,每一级被视为一种状态,两次连续爆管的时间间隔认为是状态i一1到状态i的持续时间。sem.一MarkoV过程认为时间间隔t。与以前的爆管时间间隔t。是完全独立的,只与爆管的级别i有 a sgmi—MarkOV 关。从安装到第一次爆管的时间t.被模拟成三个参数的gamma分布,接下来的爆管 时间间隔t.(i>1)被模拟成参数为1/入。的指数分布。爆管次随着i的增加而增加, 这就意味着管段以前的爆管次数越多,预计到下次爆管的时间越短。 | |
2.4温度影响统计模型
温度与爆管事故的发生密切相关,许多人对温度影响爆管过程进行了研究。例如:WalSld和Peliccia提出管道爆管率可能与给定年份的最大冰冻穿透深度相关。他们把年爆管 率和最冷月的空气温度联系在一起,以管龄和空气温度作为变量采用多元回归的方法,建立 了下式:
(2)
式中,t是管龄,N(t0)是管道安装年内每千米的爆管次数,T是最冷月的平均气温,A、B 是常数。
4.应用举例
国外某供水部门所管辖的范围共划分为9个供水区。总共包括18,408个管道维护数据 ~ 73 — 记录,管道总长2,406峰m。因为记录数据的不完整和不一致,过滤掉一些数据,最终有 16,383个有效数据,相应管道总长度为2,038km。9个区域中的8个供水区的爆管数据记 录时间区间为1993—96年,只有一个供水区的数据(称之为Z区)记录时间为1973—96 年,共计24年。供水区Z包括2,430根管段,共计298km的管段。考虑到对只有4年的管 道维护数据的8个供水进行统计分析欠充分,因此用Z区域的l 973—96年数据建立爆管数 学模型,然后用于其他8个区预测1993—96年及未来爆管率。
把所有有效数据的管道分为16个组,建立每组的爆管模型进行预测。为了建立模型假 设爆管率随时间程指数增长。如式:
其中N(t);是i组管段在t年的修 复次数,N(t0)i是i组管段在t0年的N(t)i值,a是组i的爆管率增长系数(年-1)。预测结果如表5。
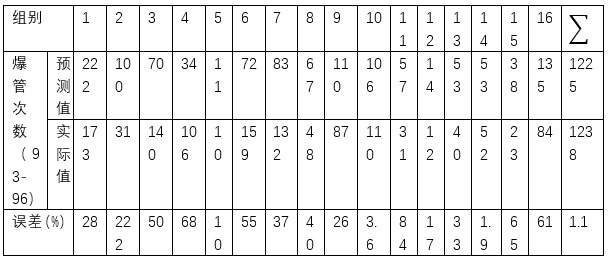
表5 预测值与实际值的比较
可以看出总的爆管预测次数于实际是基本吻合的,但每一组管道预测值的准确程度不 一。通常情况下,理论上计算出来的较高事故率的管段总会在实际情况下表现出较高的事故 率。
5.结论
爆管分析预测的最终目标是建立更具科学性和准确性的物理模型。一个真正的物理模型 应该包括所有导致爆管的因素,且应避免在建立模型的过程中采用统计的方法。然而其前提 条件是要有足够的有效的数据,而供水部门要得到这些数据付出的代价过高;另外,现有的 模型以及相关的知识对所有作用于管道的因素之间的相互作用较缺乏。所以统计模型是目前 看来较为可行的方法,特别是对规模较小的供水系统来说更是如此。
建立爆管预测统计模型的要求包括:(1)准确的管道特性数据,如管长、管径、管材等 等;(2)准确的、时间足够长的管道维护历史记录,许多供水部门缺乏严格的管道维护历史 记录,特别是那些敷设年代已久的管道。(3)要有选择地使用已有的管道维护历史数据记 录,例如在有些模型中不应考虑管道安装初期的爆管记录;(4)建立合理的管道分组原则, 对已有的爆管历史数据记录进行的分组。(5)选择合适的预测模型。对于爆管预测可以采用 的模型较多,但是我们选择的模型应该是对现有的数据拟合的好,过去的经验也说明该模型能对预测的管网给予很好的描述,数学上该模型处理方便,使用该模型时涉及到的计算复杂 程度是可以接受的,有许多与该模型相关的统计方法可以用等等。
值得注意的是,有研究发现预测结果和实际观测结果的比较表明,长期的维护数据记录 文档得到的结果不一定比短期维护数据记录文档得到的结果好,原因在于近年来供水部门开 始重视对维护数据的记录,爆管记录的完整性、准确性提高。有些因素可能会以共同的方式 影响管网,但是每个管网还有它们各自特定的因素在起作用。从一个供水部门得到的结论也 不能直接用于其他供水部门。