Wanderer001

torch.nn、(一)

参考 torch.nn、(一) - 云+社区 - 腾讯云

torch.nn

Parameters

Containers

Module

Sequential

ModuleList

ModuleDict

ParameterList

ParameterDict

Convolution layers

Conv1d

Conv2d

Conv3d

ConvTranspose1d

ConvTranspose2d

ConvTranspose3d

Unfold

Fold

Pooling layers

MaxPool1d

MaxPool2d

MaxPool3d

MaxUnpool1d

MaxUnpool2d

MaxUnpool3d

AvgPool1d

AvgPool2d

AvgPool3d

FractionalMaxPool2d

LPPool1d

LPPool2d

AdaptiveMaxPool1d

AdaptiveMaxPool2d

AdaptiveMaxPool3d

AdaptiveAvgPool1d

AdaptiveAvgPool2d

AdaptiveAvgPool3d

Padding layers

ReflectionPad1d

ReflectionPad2d

ReplicationPad1d

ReplicationPad2d

ReplicationPad3d

ZeroPad2d

ConstantPad1d

ConstantPad2d

ConstantPad3d

Non-linear activations (weighted sum, nonlinearity)

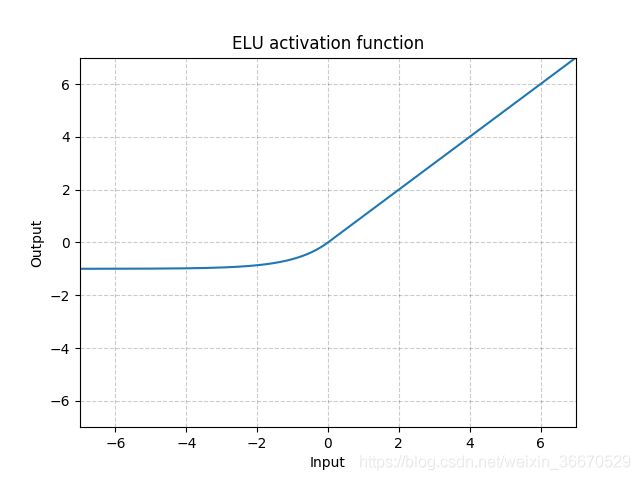
ELU

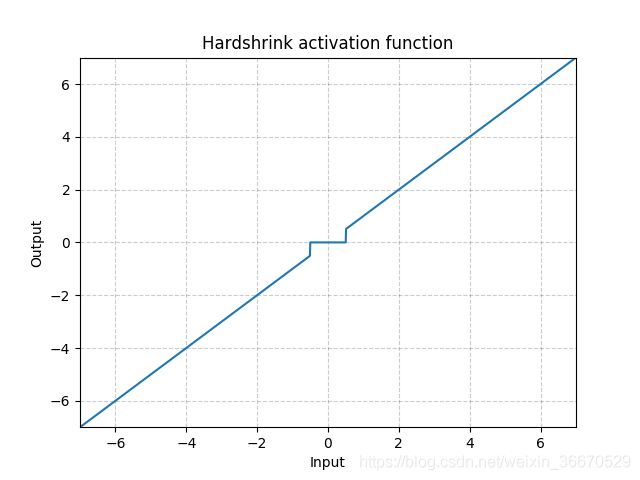
Hardshrink

Hardtanh

LeakyReLU

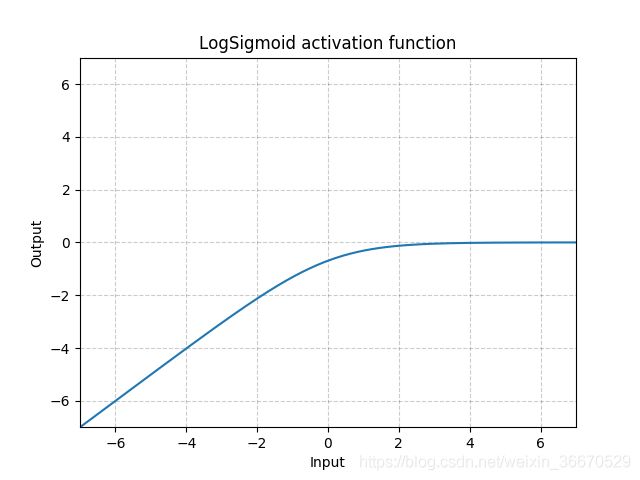
LogSigmoid

MultiheadAttention

PReLU

ReLU

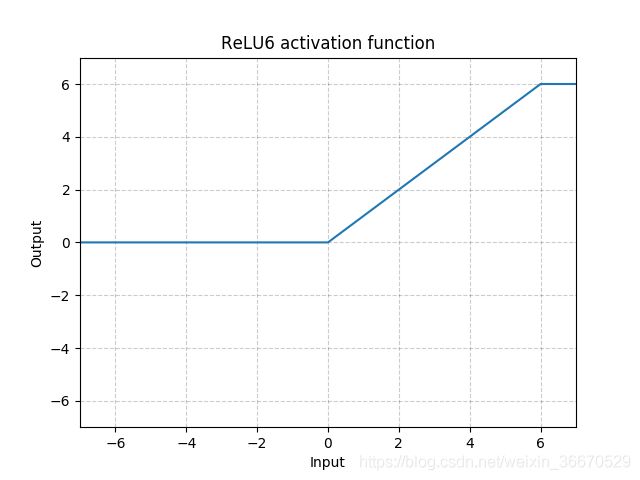
ReLU6

RReLU

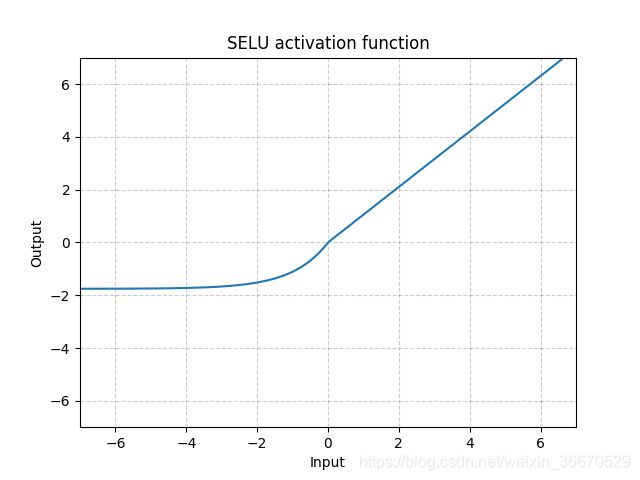
SELU

CELU

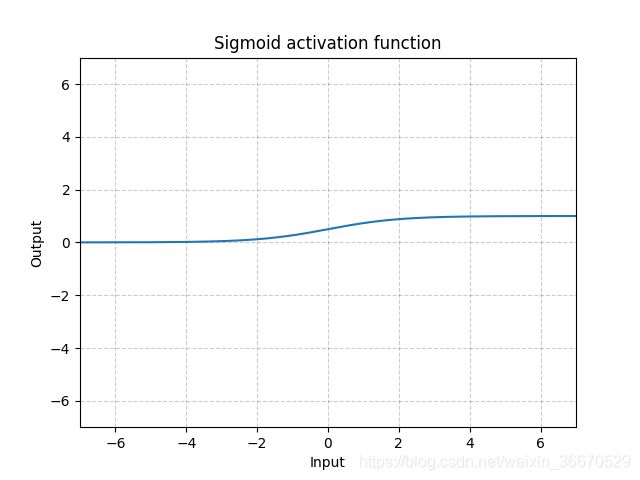
Sigmoid

Softplus

Softshrink

Softsign

Tanh

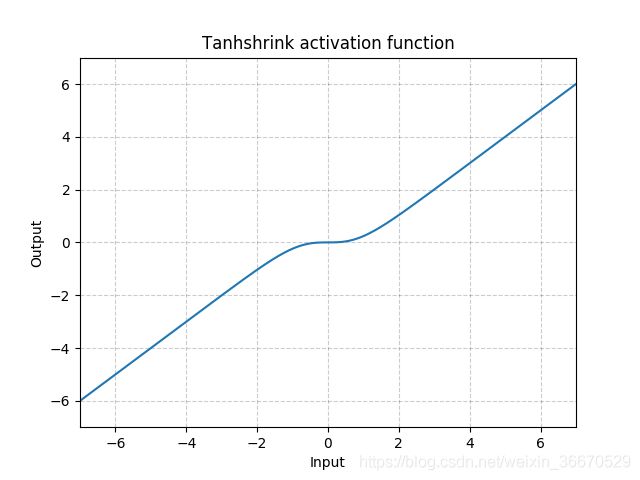
Tanhshrink

Threshold

Non-linear activations (other)

Softmin

Softmax

Softmax2d

LogSoftmax

AdaptiveLogSoftmaxWithLoss

Normalization layers

BatchNorm1d

BatchNorm2d

BatchNorm3d

GroupNorm

SyncBatchNorm

InstanceNorm1d

InstanceNorm2d

InstanceNorm3d

LayerNorm

LocalResponseNorm

torch.nn

Parameters

class torch.nn.Parameter[source]

A kind of Tensor that is to be considered a module parameter.

Parameters are Tensor subclasses, that have a very special property when used with Module s - when they’re assigned as Module attributes they are automatically added to the list of its parameters, and will appear e.g. in parameters() iterator. Assigning a Tensor doesn’t have such effect. This is because one might want to cache some temporary state, like last hidden state of the RNN, in the model. If there was no such class as Parameter, these temporaries would get registered too.

Parameters

data (Tensor) – parameter tensor.
requires_grad (bool, optional) – if the parameter requires gradient. See Excluding subgraphs from backward for more details. Default: True

Containers

Module

class torch.nn.Module[source]

Base class for all neural network modules.

Your models should also subclass this class.

Modules can also contain other Modules, allowing to nest them in a tree structure. You can assign the submodules as regular attributes:

import torch.nn as nn
import torch.nn.functional as F

class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.conv1 = nn.Conv2d(1, 20, 5)
        self.conv2 = nn.Conv2d(20, 20, 5)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        return F.relu(self.conv2(x))

Submodules assigned in this way will be registered, and will have their parameters converted too when you call to(), etc.

add_module(name, module)[source]

Adds a child module to the current module.

The module can be accessed as an attribute using the given name.

Parameters

name (string) – name of the child module. The child module can be accessed from this module using the given name
module (Module) – child module to be added to the module.

apply(fn)[source]

Applies fn recursively to every submodule (as returned by .children()) as well as self. Typical use includes initializing the parameters of a model (see also torch-nn-init).

Parameters

fn (Module -> None) – function to be applied to each submodule

Returns

self

Return type

Module

Example:

>>> def init_weights(m):
>>>     print(m)
>>>     if type(m) == nn.Linear:
>>>         m.weight.data.fill_(1.0)
>>>         print(m.weight)
>>> net = nn.Sequential(nn.Linear(2, 2), nn.Linear(2, 2))
>>> net.apply(init_weights)
Linear(in_features=2, out_features=2, bias=True)
Parameter containing:
tensor([[ 1.,  1.],
        [ 1.,  1.]])
Linear(in_features=2, out_features=2, bias=True)
Parameter containing:
tensor([[ 1.,  1.],
        [ 1.,  1.]])
Sequential(
  (0): Linear(in_features=2, out_features=2, bias=True)
  (1): Linear(in_features=2, out_features=2, bias=True)
)
Sequential(
  (0): Linear(in_features=2, out_features=2, bias=True)
  (1): Linear(in_features=2, out_features=2, bias=True)
)

buffers(recurse=True)[source]

Returns an iterator over module buffers.

Parameters

recurse (bool) – if True, then yields buffers of this module and all submodules. Otherwise, yields only buffers that are direct members of this module.

Yields

torch.Tensor – module buffer

Example:

>>> for buf in model.buffers():
>>>     print(type(buf.data), buf.size())
 (20L,)
 (20L, 1L, 5L, 5L)

children()[source]

Returns an iterator over immediate children modules.

Yields

Module – a child module

cpu()[source]

Moves all model parameters and buffers to the CPU.

Returns

self

Return type

Module

cuda(device=None)[source]

Moves all model parameters and buffers to the GPU.

This also makes associated parameters and buffers different objects. So it should be called before constructing optimizer if the module will live on GPU while being optimized.

Parameters

device (int, optional) – if specified, all parameters will be copied to that device

Returns

self

Return type

Module

double()[source]

Casts all floating point parameters and buffers to double datatype.

Returns

self

Return type

Module

dump_patches = False

This allows better BC support for load_state_dict(). In state_dict(), the version number will be saved as in the attribute _metadata of the returned state dict, and thus pickled. _metadata is a dictionary with keys that follow the naming convention of state dict. See _load_from_state_dict on how to use this information in loading.

If new parameters/buffers are added/removed from a module, this number shall be bumped, and the module’s _load_from_state_dict method can compare the version number and do appropriate changes if the state dict is from before the change.

eval()[source]

Sets the module in evaluation mode.

This has any effect only on certain modules. See documentations of particular modules for details of their behaviors in training/evaluation mode, if they are affected, e.g. Dropout, BatchNorm, etc.

This is equivalent with self.train(False).

Returns

self

Return type

Module

extra_repr()[source]

Set the extra representation of the module

To print customized extra information, you should reimplement this method in your own modules. Both single-line and multi-line strings are acceptable.

float()[source]

Casts all floating point parameters and buffers to float datatype.

Returns

self

Return type

Module

forward(*input)[source]

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

half()[source]

Casts all floating point parameters and buffers to half datatype.

Returns

self

Return type

Module

load_state_dict(state_dict, strict=True)[source]

Copies parameters and buffers from state_dict into this module and its descendants. If strict is True, then the keys of state_dict must exactly match the keys returned by this module’s state_dict() function.

Parameters

state_dict (dict) – a dict containing parameters and persistent buffers.
strict (bool, optional) – whether to strictly enforce that the keys in state_dict match the keys returned by this module’s state_dict() function. Default: True

Returns

missing_keys is a list of str containing the missing keys
unexpected_keys is a list of str containing the unexpected keys

Return type

NamedTuple with missing_keys and unexpected_keys fields

modules()[source]

Returns an iterator over all modules in the network.

Yields

Module – a module in the network

Note

Duplicate modules are returned only once. In the following example, l will be returned only once.

Example:

>>> l = nn.Linear(2, 2)
>>> net = nn.Sequential(l, l)
>>> for idx, m in enumerate(net.modules()):
        print(idx, '->', m)

0 -> Sequential(
  (0): Linear(in_features=2, out_features=2, bias=True)
  (1): Linear(in_features=2, out_features=2, bias=True)
)
1 -> Linear(in_features=2, out_features=2, bias=True)

named_buffers(prefix='', recurse=True)[source]

Returns an iterator over module buffers, yielding both the name of the buffer as well as the buffer itself.

Parameters

prefix (str) – prefix to prepend to all buffer names.
recurse (bool) – if True, then yields buffers of this module and all submodules. Otherwise, yields only buffers that are direct members of this module.

Yields

(string, torch.Tensor) – Tuple containing the name and buffer

Example:

>>> for name, buf in self.named_buffers():
>>>    if name in ['running_var']:
>>>        print(buf.size())

named_children()[source]

Returns an iterator over immediate children modules, yielding both the name of the module as well as the module itself.

Yields

(string, Module) – Tuple containing a name and child module

Example:

>>> for name, module in model.named_children():
>>>     if name in ['conv4', 'conv5']:
>>>         print(module)

named_modules(memo=None, prefix='')[source]

Returns an iterator over all modules in the network, yielding both the name of the module as well as the module itself.

Yields

(string, Module) – Tuple of name and module

Note

Duplicate modules are returned only once. In the following example, l will be returned only once.

Example:

>>> l = nn.Linear(2, 2)
>>> net = nn.Sequential(l, l)
>>> for idx, m in enumerate(net.named_modules()):
        print(idx, '->', m)

0 -> ('', Sequential(
  (0): Linear(in_features=2, out_features=2, bias=True)
  (1): Linear(in_features=2, out_features=2, bias=True)
))
1 -> ('0', Linear(in_features=2, out_features=2, bias=True))

named_parameters(prefix='', recurse=True)[source]

Returns an iterator over module parameters, yielding both the name of the parameter as well as the parameter itself.

Parameters

prefix (str) – prefix to prepend to all parameter names.
recurse (bool) – if True, then yields parameters of this module and all submodules. Otherwise, yields only parameters that are direct members of this module.

Yields

(string, Parameter) – Tuple containing the name and parameter

Example:

>>> for name, param in self.named_parameters():
>>>    if name in ['bias']:
>>>        print(param.size())

parameters(recurse=True)[source]

Returns an iterator over module parameters.

This is typically passed to an optimizer.

Parameters

recurse (bool) – if True, then yields parameters of this module and all submodules. Otherwise, yields only parameters that are direct members of this module.

Yields

Parameter – module parameter

Example:

>>> for param in model.parameters():
>>>     print(type(param.data), param.size())
 (20L,)
 (20L, 1L, 5L, 5L)

register_backward_hook(hook)[source]

Registers a backward hook on the module.

The hook will be called every time the gradients with respect to module inputs are computed. The hook should have the following signature:

hook(module, grad_input, grad_output) -> Tensor or None

The grad_input and grad_output may be tuples if the module has multiple inputs or outputs. The hook should not modify its arguments, but it can optionally return a new gradient with respect to input that will be used in place of grad_input in subsequent computations.

Returns

a handle that can be used to remove the added hook by calling handle.remove()

Return type

torch.utils.hooks.RemovableHandle

Warning

The current implementation will not have the presented behavior for complex Module that perform many operations. In some failure cases, grad_input and grad_output will only contain the gradients for a subset of the inputs and outputs. For such Module, you should use torch.Tensor.register_hook() directly on a specific input or output to get the required gradients.

register_buffer(name, tensor)[source]

Adds a persistent buffer to the module.

This is typically used to register a buffer that should not to be considered a model parameter. For example, BatchNorm’s running_mean is not a parameter, but is part of the persistent state.

Buffers can be accessed as attributes using given names.

Parameters

name (string) – name of the buffer. The buffer can be accessed from this module using the given name
tensor (Tensor) – buffer to be registered.

Example:

>>> self.register_buffer('running_mean', torch.zeros(num_features))

register_forward_hook(hook)[source]

Registers a forward hook on the module.

The hook will be called every time after forward() has computed an output. It should have the following signature:

hook(module, input, output) -> None or modified output

The hook can modify the output. It can modify the input inplace but it will not have effect on forward since this is called after forward() is called.

Returns

a handle that can be used to remove the added hook by calling handle.remove()

Return type

torch.utils.hooks.RemovableHandle

register_forward_pre_hook(hook)[source]

Registers a forward pre-hook on the module.

The hook will be called every time before forward() is invoked. It should have the following signature:

hook(module, input) -> None or modified input

The hook can modify the input. User can either return a tuple or a single modified value in the hook. We will wrap the value into a tuple if a single value is returned(unless that value is already a tuple).

Returns

a handle that can be used to remove the added hook by calling handle.remove()

Return type

torch.utils.hooks.RemovableHandle

register_parameter(name, param)[source]

Adds a parameter to the module.

The parameter can be accessed as an attribute using given name.

Parameters

name (string) – name of the parameter. The parameter can be accessed from this module using the given name
param (Parameter) – parameter to be added to the module.

requires_grad_(requires_grad=True)[source]

Change if autograd should record operations on parameters in this module.

This method sets the parameters’ requires_grad attributes in-place.

This method is helpful for freezing part of the module for finetuning or training parts of a model individually (e.g., GAN training).

Parameters

requires_grad (bool) – whether autograd should record operations on parameters in this module. Default: True.

Returns

self

Return type

Module

state_dict(destination=None, prefix='', keep_vars=False)[source]

Returns a dictionary containing a whole state of the module.

Both parameters and persistent buffers (e.g. running averages) are included. Keys are corresponding parameter and buffer names.

Returns

a dictionary containing a whole state of the module

Return type

dict

Example:

>>> module.state_dict().keys()
['bias', 'weight']

to(*args, **kwargs)[source]

Moves and/or casts the parameters and buffers.

This can be called as

to(device=None, dtype=None, non_blocking=False)[source]

to(dtype, non_blocking=False)[source]

to(tensor, non_blocking=False)[source]

Its signature is similar to torch.Tensor.to(), but only accepts floating point desired dtype s. In addition, this method will only cast the floating point parameters and buffers to dtype (if given). The integral parameters and buffers will be moved device, if that is given, but with dtypes unchanged. When non_blocking is set, it tries to convert/move asynchronously with respect to the host if possible, e.g., moving CPU Tensors with pinned memory to CUDA devices.

See below for examples.

Note

This method modifies the module in-place.

Parameters

device (torch.device) – the desired device of the parameters and buffers in this module
dtype (torch.dtype) – the desired floating point type of the floating point parameters and buffers in this module
tensor (torch.Tensor) – Tensor whose dtype and device are the desired dtype and device for all parameters and buffers in this module

Returns

self

Return type

Module

Example:

>>> linear = nn.Linear(2, 2)
>>> linear.weight
Parameter containing:
tensor([[ 0.1913, -0.3420],
        [-0.5113, -0.2325]])
>>> linear.to(torch.double)
Linear(in_features=2, out_features=2, bias=True)
>>> linear.weight
Parameter containing:
tensor([[ 0.1913, -0.3420],
        [-0.5113, -0.2325]], dtype=torch.float64)
>>> gpu1 = torch.device("cuda:1")
>>> linear.to(gpu1, dtype=torch.half, non_blocking=True)
Linear(in_features=2, out_features=2, bias=True)
>>> linear.weight
Parameter containing:
tensor([[ 0.1914, -0.3420],
        [-0.5112, -0.2324]], dtype=torch.float16, device='cuda:1')
>>> cpu = torch.device("cpu")
>>> linear.to(cpu)
Linear(in_features=2, out_features=2, bias=True)
>>> linear.weight
Parameter containing:
tensor([[ 0.1914, -0.3420],
        [-0.5112, -0.2324]], dtype=torch.float16)

train(mode=True)[source]

Sets the module in training mode.

This has any effect only on certain modules. See documentations of particular modules for details of their behaviors in training/evaluation mode, if they are affected, e.g. Dropout, BatchNorm, etc.

Parameters

mode (bool) – whether to set training mode (True) or evaluation mode (False). Default: True.

Returns

self

Return type

Module

type(dst_type)[source]

Casts all parameters and buffers to dst_type.

Parameters

dst_type (type or string) – the desired type

Returns

self

Return type

Module

zero_grad()[source]

Sets gradients of all model parameters to zero.

Sequential

class torch.nn.Sequential(*args)[source]

A sequential container. Modules will be added to it in the order they are passed in the constructor. Alternatively, an ordered dict of modules can also be passed in.

To make it easier to understand, here is a small example:

# Example of using Sequential
model = nn.Sequential(
          nn.Conv2d(1,20,5),
          nn.ReLU(),
          nn.Conv2d(20,64,5),
          nn.ReLU()
        )

# Example of using Sequential with OrderedDict
model = nn.Sequential(OrderedDict([
          ('conv1', nn.Conv2d(1,20,5)),
          ('relu1', nn.ReLU()),
          ('conv2', nn.Conv2d(20,64,5)),
          ('relu2', nn.ReLU())
        ]))

ModuleList

class torch.nn.ModuleList(modules=None)[source]

Holds submodules in a list.

ModuleList can be indexed like a regular Python list, but modules it contains are properly registered, and will be visible by all Module methods.

Parameters

modules (iterable, optional) – an iterable of modules to add

Example:

class MyModule(nn.Module):
    def __init__(self):
        super(MyModule, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(10, 10) for i in range(10)])

    def forward(self, x):
        # ModuleList can act as an iterable, or be indexed using ints
        for i, l in enumerate(self.linears):
            x = self.linears[i // 2](x) + l(x)
        return x

append(module)[source]

Appends a given module to the end of the list.

Parameters

module (nn.Module) – module to append

extend(modules)[source]

Appends modules from a Python iterable to the end of the list.

Parameters

modules (iterable) – iterable of modules to append

insert(index, module)[source]

Insert a given module before a given index in the list.

Parameters

index (int) – index to insert.
module (nn.Module) – module to insert

ModuleDict

class torch.nn.ModuleDict(modules=None)[source]

Holds submodules in a dictionary.

ModuleDict can be indexed like a regular Python dictionary, but modules it contains are properly registered, and will be visible by all Module methods.

ModuleDict is an ordered dictionary that respects

the order of insertion, and
in update(), the order of the merged OrderedDict or another ModuleDict (the argument to update()).

Note that update() with other unordered mapping types (e.g., Python’s plain dict) does not preserve the order of the merged mapping.

Parameters

modules (iterable, optional) – a mapping (dictionary) of (string: module) or an iterable of key-value pairs of type (string, module)

Example:

class MyModule(nn.Module):
    def __init__(self):
        super(MyModule, self).__init__()
        self.choices = nn.ModuleDict({
                'conv': nn.Conv2d(10, 10, 3),
                'pool': nn.MaxPool2d(3)
        })
        self.activations = nn.ModuleDict([
                ['lrelu', nn.LeakyReLU()],
                ['prelu', nn.PReLU()]
        ])

    def forward(self, x, choice, act):
        x = self.choices[choice](x)
        x = self.activations[act](x)
        return x

clear()[source]

Remove all items from the ModuleDict.

items()[source]

Return an iterable of the ModuleDict key/value pairs.

keys()[source]

Return an iterable of the ModuleDict keys.

pop(key)[source]

Remove key from the ModuleDict and return its module.

Parameters

key (string) – key to pop from the ModuleDict

update(modules)[source]

Update the ModuleDict with the key-value pairs from a mapping or an iterable, overwriting existing keys.

Note

If modules is an OrderedDict, a ModuleDict, or an iterable of key-value pairs, the order of new elements in it is preserved.

Parameters

modules (iterable) – a mapping (dictionary) from string to Module, or an iterable of key-value pairs of type (string, Module)

values()[source]

Return an iterable of the ModuleDict values.

ParameterList

class torch.nn.ParameterList(parameters=None)[source]

Holds parameters in a list.

ParameterList can be indexed like a regular Python list, but parameters it contains are properly registered, and will be visible by all Module methods.

Parameters

parameters (iterable, optional) – an iterable of Parameter to add

Example:

class MyModule(nn.Module):
    def __init__(self):
        super(MyModule, self).__init__()
        self.params = nn.ParameterList([nn.Parameter(torch.randn(10, 10)) for i in range(10)])

    def forward(self, x):
        # ParameterList can act as an iterable, or be indexed using ints
        for i, p in enumerate(self.params):
            x = self.params[i // 2].mm(x) + p.mm(x)
        return x

append(parameter)[source]

Appends a given parameter at the end of the list.

Parameters

parameter (nn.Parameter) – parameter to append

extend(parameters)[source]

Appends parameters from a Python iterable to the end of the list.

Parameters

parameters (iterable) – iterable of parameters to append

ParameterDict

class torch.nn.ParameterDict(parameters=None)[source]

Holds parameters in a dictionary.

ParameterDict can be indexed like a regular Python dictionary, but parameters it contains are properly registered, and will be visible by all Module methods.

ParameterDict is an ordered dictionary that respects

the order of insertion, and
in update(), the order of the merged OrderedDict or another ParameterDict (the argument to update()).

Note that update() with other unordered mapping types (e.g., Python’s plain dict) does not preserve the order of the merged mapping.

Parameters

parameters (iterable, optional) – a mapping (dictionary) of (string : Parameter) or an iterable of key-value pairs of type (string, Parameter)

Example:

class MyModule(nn.Module):
    def __init__(self):
        super(MyModule, self).__init__()
        self.params = nn.ParameterDict({
                'left': nn.Parameter(torch.randn(5, 10)),
                'right': nn.Parameter(torch.randn(5, 10))
        })

    def forward(self, x, choice):
        x = self.params[choice].mm(x)
        return x

clear()[source]

Remove all items from the ParameterDict.

items()[source]

Return an iterable of the ParameterDict key/value pairs.

keys()[source]

Return an iterable of the ParameterDict keys.

pop(key)[source]

Remove key from the ParameterDict and return its parameter.

Parameters

key (string) – key to pop from the ParameterDict

update(parameters)[source]

Update the ParameterDict with the key-value pairs from a mapping or an iterable, overwriting existing keys.

Note

If parameters is an OrderedDict, a ParameterDict, or an iterable of key-value pairs, the order of new elements in it is preserved.

Parameters

parameters (iterable) – a mapping (dictionary) from string to Parameter, or an iterable of key-value pairs of type (string, Parameter)

values()[source]

Return an iterable of the ParameterDict values.

Convolution layers

Conv1d

class torch.nn.Conv1d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')[source]

Applies a 1D convolution over an input signal composed of several input planes.

In the simplest case, the output value of the layer with input size (N,Cin,L)(N, C_{\text{in}}, L)(N,Cin,L) and output (N,Cout,Lout)(N, C_{\text{out}}, L_{\text{out}})(N,Cout,Lout) can be precisely described as:

out(Ni,Coutj)=bias(Coutj)+∑k=0Cin−1weight(Coutj,k)⋆input(Ni,k)\text{out}(N_i, C_{\text{out}_j}) = \text{bias}(C_{\text{out}_j}) + \sum_{k = 0}^{C_{in} - 1} \text{weight}(C_{\text{out}_j}, k) \star \text{input}(N_i, k) out(Ni,Coutj)=bias(Coutj)+k=0∑Cin−1weight(Coutj,k)⋆input(Ni,k)

where ⋆\star⋆ is the valid cross-correlation operator, NNN is a batch size, CCC denotes a number of channels, LLL is a length of signal sequence.

stride controls the stride for the cross-correlation, a single number or a one-element tuple.
padding controls the amount of implicit zero-paddings on both sides for padding number of points.
dilation controls the spacing between the kernel points; also known as the à trous algorithm. It is harder to describe, but this link has a nice visualization of what dilation does.
groups controls the connections between inputs and outputs. in_channels and out_channels must both be divisible by groups. For example,
- At groups=1, all inputs are convolved to all outputs.
- At groups=2, the operation becomes equivalent to having two conv layers side by side, each seeing half the input channels, and producing half the output channels, and both subsequently concatenated.
- At groups= in_channels, each input channel is convolved with its own set of filters, of size ⌊out_channelsin_channels⌋\left\lfloor\frac{out\_channels}{in\_channels}\right\rfloor⌊in_channelsout_channels⌋ .

Note

Depending of the size of your kernel, several (of the last) columns of the input might be lost, because it is a valid cross-correlation, and not a full cross-correlation. It is up to the user to add proper padding.

Note

When groups == in_channels and out_channels == K * in_channels, where K is a positive integer, this operation is also termed in literature as depthwise convolution.

In other words, for an input of size (N,Cin,Lin)(N, C_{in}, L_{in})(N,Cin,Lin) , a depthwise convolution with a depthwise multiplier K, can be constructed by arguments (Cin=Cin,Cout=Cin×K,...,groups=Cin)(C_\text{in}=C_{in}, C_\text{out}=C_{in} \times K, ..., \text{groups}=C_{in})(Cin=Cin,Cout=Cin×K,...,groups=Cin) .

Note

In some circumstances when using the CUDA backend with CuDNN, this operator may select a nondeterministic algorithm to increase performance. If this is undesirable, you can try to make the operation deterministic (potentially at a performance cost) by setting torch.backends.cudnn.deterministic = True. Please see the notes on Reproducibility for background.

Parameters

in_channels (int) – Number of channels in the input image
out_channels (int) – Number of channels produced by the convolution
kernel_size (int or tuple) – Size of the convolving kernel
stride (int or tuple, optional) – Stride of the convolution. Default: 1
padding (int or tuple, optional) – Zero-padding added to both sides of the input. Default: 0
padding_mode (string, optional) – zeros
dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1
groups (int, optional) – Number of blocked connections from input channels to output channels. Default: 1
bias (bool, optional) – If True, adds a learnable bias to the output. Default: True

Shape:

Input: (N,Cin,Lin)(N, C_{in}, L_{in})(N,Cin,Lin)
Output: (N,Cout,Lout)(N, C_{out}, L_{out})(N,Cout,Lout) where

Lout=⌊Lin+2×padding−dilation×(kernel_size−1)−1stride+1⌋L_{out} = \left\lfloor\frac{L_{in} + 2 \times \text{padding} - \text{dilation} \times (\text{kernel\_size} - 1) - 1}{\text{stride}} + 1\right\rfloor Lout=⌊strideLin+2×padding−dilation×(kernel_size−1)−1+1⌋

Variables

~Conv1d.weight (Tensor) – the learnable weights of the module of shape (out_channels,in_channelsgroups,kernel_size)(\text{out\_channels}, \frac{\text{in\_channels}}{\text{groups}}, \text{kernel\_size})(out_channels,groupsin_channels,kernel_size) . The values of these weights are sampled from U(−k,k)\mathcal{U}(-\sqrt{k}, \sqrt{k})U(−k

) where k=1Cin∗kernel_sizek = \frac{1}{C_\text{in} * \text{kernel\_size}}k=Cin∗kernel_size1
~Conv1d.bias (Tensor) – the learnable bias of the module of shape (out_channels). If bias is True, then the values of these weights are sampled from U(−k,k)\mathcal{U}(-\sqrt{k}, \sqrt{k})U(−k
,k
Examples:
```
>>> m = nn.Conv1d(16, 33, 3, stride=2)
>>> input = torch.randn(20, 16, 50)
>>> output = m(input)
```
Conv2d

class torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')[source]

Applies a 2D convolution over an input signal composed of several input planes.

In the simplest case, the output value of the layer with input size (N,Cin,H,W)(N, C_{\text{in}}, H, W)(N,Cin,H,W) and output (N,Cout,Hout,Wout)(N, C_{\text{out}}, H_{\text{out}}, W_{\text{out}})(N,Cout,Hout,Wout) can be precisely described as:

out(Ni,Coutj)=bias(Coutj)+∑k=0Cin−1weight(Coutj,k)⋆input(Ni,k)\text{out}(N_i, C_{\text{out}_j}) = \text{bias}(C_{\text{out}_j}) + \sum_{k = 0}^{C_{\text{in}} - 1} \text{weight}(C_{\text{out}_j}, k) \star \text{input}(N_i, k) out(Ni,Coutj)=bias(Coutj)+k=0∑Cin−1weight(Coutj,k)⋆input(Ni,k)

where ⋆\star⋆ is the valid 2D cross-correlation operator, NNN is a batch size, CCC denotes a number of channels, HHH is a height of input planes in pixels, and WWW is width in pixels.

The parameters kernel_size, stride, padding, dilation can either be:
- a single int – in which case the same value is used for the height and width dimension
- a tuple of two ints – in which case, the first int is used for the height dimension, and the second int for the width dimension
Note

Depending of the size of your kernel, several (of the last) columns of the input might be lost, because it is a valid cross-correlation, and not a full cross-correlation. It is up to the user to add proper padding.

Note

When groups == in_channels and out_channels == K * in_channels, where K is a positive integer, this operation is also termed in literature as depthwise convolution.

In other words, for an input of size (N,Cin,Hin,Win)(N, C_{in}, H_{in}, W_{in})(N,Cin,Hin,Win) , a depthwise convolution with a depthwise multiplier K, can be constructed by arguments (in_channels=Cin,out_channels=Cin×K,...,groups=Cin)(in\_channels=C_{in}, out\_channels=C_{in} \times K, ..., groups=C_{in})(in_channels=Cin,out_channels=Cin×K,...,groups=Cin) .

Note

In some circumstances when using the CUDA backend with CuDNN, this operator may select a nondeterministic algorithm to increase performance. If this is undesirable, you can try to make the operation deterministic (potentially at a performance cost) by setting torch.backends.cudnn.deterministic = True. Please see the notes on Reproducibility for background.

Parameters

Shape:

Variables
,k
- ) where k=1Cin∗kernel_sizek = \frac{1}{C_\text{in} * \text{kernel\_size}}k=Cin∗kernel_size1
- stride controls the stride for the cross-correlation, a single number or a tuple.
- padding controls the amount of implicit zero-paddings on both sides for padding number of points for each dimension.
- dilation controls the spacing between the kernel points; also known as the à trous algorithm. It is harder to describe, but this link has a nice visualization of what dilation does.
- groups controls the connections between inputs and outputs. in_channels and out_channels must both be divisible by groups. For example,
  - At groups=1, all inputs are convolved to all outputs.
  - At groups=2, the operation becomes equivalent to having two conv layers side by side, each seeing half the input channels, and producing half the output channels, and both subsequently concatenated.
  - At groups= in_channels, each input channel is convolved with its own set of filters, of size: ⌊out_channelsin_channels⌋\left\lfloor\frac{out\_channels}{in\_channels}\right\rfloor⌊in_channelsout_channels⌋ .
- in_channels (int) – Number of channels in the input image
- out_channels (int) – Number of channels produced by the convolution
- kernel_size (int or tuple) – Size of the convolving kernel
- stride (int or tuple, optional) – Stride of the convolution. Default: 1
- padding (int or tuple, optional) – Zero-padding added to both sides of the input. Default: 0
- padding_mode (string, optional) – zeros
- dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1
- groups (int, optional) – Number of blocked connections from input channels to output channels. Default: 1
- bias (bool, optional) – If True, adds a learnable bias to the output. Default: True
- Input: (N,Cin,Hin,Win)(N, C_{in}, H_{in}, W_{in})(N,Cin,Hin,Win)
- Output: (N,Cout,Hout,Wout)(N, C_{out}, H_{out}, W_{out})(N,Cout,Hout,Wout) where
  
  Hout=⌊Hin+2×padding[0]−dilation[0]×(kernel_size[0]−1)−1stride[0]+1⌋H_{out} = \left\lfloor\frac{H_{in} + 2 \times \text{padding}[0] - \text{dilation}[0] \times (\text{kernel\_size}[0] - 1) - 1}{\text{stride}[0]} + 1\right\rfloor Hout=⌊stride[0]Hin+2×padding[0]−dilation[0]×(kernel_size[0]−1)−1+1⌋
  
  Wout=⌊Win+2×padding[1]−dilation[1]×(kernel_size[1]−1)−1stride[1]+1⌋W_{out} = \left\lfloor\frac{W_{in} + 2 \times \text{padding}[1] - \text{dilation}[1] \times (\text{kernel\_size}[1] - 1) - 1}{\text{stride}[1]} + 1\right\rfloor Wout=⌊stride[1]Win+2×padding[1]−dilation[1]×(kernel_size[1]−1)−1+1⌋
- ~Conv2d.weight (Tensor) – the learnable weights of the module of shape (out_channels,in_channelsgroups,(\text{out\_channels}, \frac{\text{in\_channels}}{\text{groups}},(out_channels,groupsin_channels, kernel_size[0],kernel_size[1])\text{kernel\_size[0]}, \text{kernel\_size[1]})kernel_size[0],kernel_size[1]) . The values of these weights are sampled from U(−k,k)\mathcal{U}(-\sqrt{k}, \sqrt{k})U(−k
) where k=1Cin∗∏i=01kernel_size[i]k = \frac{1}{C_\text{in} * \prod_{i=0}^{1}\text{kernel\_size}[i]}k=Cin∗∏i=01kernel_size[i]1
~Conv2d.bias (Tensor) – the learnable bias of the module of shape (out_channels). If bias is True, then the values of these weights are sampled from U(−k,k)\mathcal{U}(-\sqrt{k}, \sqrt{k})U(−k
,k
Examples:
```
>>> # With square kernels and equal stride
>>> m = nn.Conv2d(16, 33, 3, stride=2)
>>> # non-square kernels and unequal stride and with padding
>>> m = nn.Conv2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2))
>>> # non-square kernels and unequal stride and with padding and dilation
>>> m = nn.Conv2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2), dilation=(3, 1))
>>> input = torch.randn(20, 16, 50, 100)
>>> output = m(input)
```
Conv3d

class torch.nn.Conv3d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')[source]

Applies a 3D convolution over an input signal composed of several input planes.

In the simplest case, the output value of the layer with input size (N,Cin,D,H,W)(N, C_{in}, D, H, W)(N,Cin,D,H,W) and output (N,Cout,Dout,Hout,Wout)(N, C_{out}, D_{out}, H_{out}, W_{out})(N,Cout,Dout,Hout,Wout) can be precisely described as:

out(Ni,Coutj)=bias(Coutj)+∑k=0Cin−1weight(Coutj,k)⋆input(Ni,k)out(N_i, C_{out_j}) = bias(C_{out_j}) + \sum_{k = 0}^{C_{in} - 1} weight(C_{out_j}, k) \star input(N_i, k) out(Ni,Coutj)=bias(Coutj)+k=0∑Cin−1weight(Coutj,k)⋆input(Ni,k)

where ⋆\star⋆ is the valid 3D cross-correlation operator

The parameters kernel_size, stride, padding, dilation can either be:
- a single int – in which case the same value is used for the depth, height and width dimension
- a tuple of three ints – in which case, the first int is used for the depth dimension, the second int for the height dimension and the third int for the width dimension
Note

Depending of the size of your kernel, several (of the last) columns of the input might be lost, because it is a valid cross-correlation, and not a full cross-correlation. It is up to the user to add proper padding.

Note

When groups == in_channels and out_channels == K * in_channels, where K is a positive integer, this operation is also termed in literature as depthwise convolution.

In other words, for an input of size (N,Cin,Din,Hin,Win)(N, C_{in}, D_{in}, H_{in}, W_{in})(N,Cin,Din,Hin,Win) , a depthwise convolution with a depthwise multiplier K, can be constructed by arguments (in_channels=Cin,out_channels=Cin×K,...,groups=Cin)(in\_channels=C_{in}, out\_channels=C_{in} \times K, ..., groups=C_{in})(in_channels=Cin,out_channels=Cin×K,...,groups=Cin) .

Note

In some circumstances when using the CUDA backend with CuDNN, this operator may select a nondeterministic algorithm to increase performance. If this is undesirable, you can try to make the operation deterministic (potentially at a performance cost) by setting torch.backends.cudnn.deterministic = True. Please see the notes on Reproducibility for background.

Parameters

Shape:

Variables
,k
- ) where k=1Cin∗∏i=01kernel_size[i]k = \frac{1}{C_\text{in} * \prod_{i=0}^{1}\text{kernel\_size}[i]}k=Cin∗∏i=01kernel_size[i]1
- stride controls the stride for the cross-correlation.
- padding controls the amount of implicit zero-paddings on both sides for padding number of points for each dimension.
- dilation controls the spacing between the kernel points; also known as the à trous algorithm. It is harder to describe, but this link has a nice visualization of what dilation does.
- groups controls the connections between inputs and outputs. in_channels and out_channels must both be divisible by groups. For example,
  - At groups=1, all inputs are convolved to all outputs.
  - At groups=2, the operation becomes equivalent to having two conv layers side by side, each seeing half the input channels, and producing half the output channels, and both subsequently concatenated.
  - At groups= in_channels, each input channel is convolved with its own set of filters, of size ⌊out_channelsin_channels⌋\left\lfloor\frac{out\_channels}{in\_channels}\right\rfloor⌊in_channelsout_channels⌋ .
- in_channels (int) – Number of channels in the input image
- out_channels (int) – Number of channels produced by the convolution
- kernel_size (int or tuple) – Size of the convolving kernel
- stride (int or tuple, optional) – Stride of the convolution. Default: 1
- padding (int or tuple, optional) – Zero-padding added to all three sides of the input. Default: 0
- padding_mode (string, optional) – zeros
- dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1
- groups (int, optional) – Number of blocked connections from input channels to output channels. Default: 1
- bias (bool, optional) – If True, adds a learnable bias to the output. Default: True
- Input: (N,Cin,Din,Hin,Win)(N, C_{in}, D_{in}, H_{in}, W_{in})(N,Cin,Din,Hin,Win)
- Output: (N,Cout,Dout,Hout,Wout)(N, C_{out}, D_{out}, H_{out}, W_{out})(N,Cout,Dout,Hout,Wout) where
  
  Dout=⌊Din+2×padding[0]−dilation[0]×(kernel_size[0]−1)−1stride[0]+1⌋D_{out} = \left\lfloor\frac{D_{in} + 2 \times \text{padding}[0] - \text{dilation}[0] \times (\text{kernel\_size}[0] - 1) - 1}{\text{stride}[0]} + 1\right\rfloor Dout=⌊stride[0]Din+2×padding[0]−dilation[0]×(kernel_size[0]−1)−1+1⌋
  
  Hout=⌊Hin+2×padding[1]−dilation[1]×(kernel_size[1]−1)−1stride[1]+1⌋H_{out} = \left\lfloor\frac{H_{in} + 2 \times \text{padding}[1] - \text{dilation}[1] \times (\text{kernel\_size}[1] - 1) - 1}{\text{stride}[1]} + 1\right\rfloor Hout=⌊stride[1]Hin+2×padding[1]−dilation[1]×(kernel_size[1]−1)−1+1⌋
  
  Wout=⌊Win+2×padding[2]−dilation[2]×(kernel_size[2]−1)−1stride[2]+1⌋W_{out} = \left\lfloor\frac{W_{in} + 2 \times \text{padding}[2] - \text{dilation}[2] \times (\text{kernel\_size}[2] - 1) - 1}{\text{stride}[2]} + 1\right\rfloor Wout=⌊stride[2]Win+2×padding[2]−dilation[2]×(kernel_size[2]−1)−1+1⌋
- ~Conv3d.weight (Tensor) – the learnable weights of the module of shape (out_channels,in_channelsgroups,(\text{out\_channels}, \frac{\text{in\_channels}}{\text{groups}},(out_channels,groupsin_channels, kernel_size[0],kernel_size[1],kernel_size[2])\text{kernel\_size[0]}, \text{kernel\_size[1]}, \text{kernel\_size[2]})kernel_size[0],kernel_size[1],kernel_size[2]) . The values of these weights are sampled from U(−k,k)\mathcal{U}(-\sqrt{k}, \sqrt{k})U(−k
) where k=1Cin∗∏i=02kernel_size[i]k = \frac{1}{C_\text{in} * \prod_{i=0}^{2}\text{kernel\_size}[i]}k=Cin∗∏i=02kernel_size[i]1
~Conv3d.bias (Tensor) – the learnable bias of the module of shape (out_channels). If bias is True, then the values of these weights are sampled from U(−k,k)\mathcal{U}(-\sqrt{k}, \sqrt{k})U(−k
,k
Examples:
```
>>> # With square kernels and equal stride
>>> m = nn.Conv3d(16, 33, 3, stride=2)
>>> # non-square kernels and unequal stride and with padding
>>> m = nn.Conv3d(16, 33, (3, 5, 2), stride=(2, 1, 1), padding=(4, 2, 0))
>>> input = torch.randn(20, 16, 10, 50, 100)
>>> output = m(input)
```
ConvTranspose1d

class torch.nn.ConvTranspose1d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode='zeros')[source]

Applies a 1D transposed convolution operator over an input image composed of several input planes.

This module can be seen as the gradient of Conv1d with respect to its input. It is also known as a fractionally-strided convolution or a deconvolution (although it is not an actual deconvolution operation).

Note

Depending of the size of your kernel, several (of the last) columns of the input might be lost, because it is a valid cross-correlation, and not a full cross-correlation. It is up to the user to add proper padding.

Note

The padding argument effectively adds dilation * (kernel_size - 1) - padding amount of zero padding to both sizes of the input. This is set so that when a Conv1d and a ConvTranspose1d are initialized with same parameters, they are inverses of each other in regard to the input and output shapes. However, when stride > 1, Conv1d maps multiple input shapes to the same output shape. output_padding is provided to resolve this ambiguity by effectively increasing the calculated output shape on one side. Note that output_padding is only used to find output shape, but does not actually add zero-padding to output.

Note

In some circumstances when using the CUDA backend with CuDNN, this operator may select a nondeterministic algorithm to increase performance. If this is undesirable, you can try to make the operation deterministic (potentially at a performance cost) by setting torch.backends.cudnn.deterministic = True. Please see the notes on Reproducibility for background.

Parameters

Shape:

Variables
,k
- ) where k=1Cin∗∏i=02kernel_size[i]k = \frac{1}{C_\text{in} * \prod_{i=0}^{2}\text{kernel\_size}[i]}k=Cin∗∏i=02kernel_size[i]1
- stride controls the stride for the cross-correlation.
- padding controls the amount of implicit zero-paddings on both sides for dilation * (kernel_size - 1) - padding number of points. See note below for details.
- output_padding controls the additional size added to one side of the output shape. See note below for details.
- dilation controls the spacing between the kernel points; also known as the à trous algorithm. It is harder to describe, but this link has a nice visualization of what dilation does.
- groups controls the connections between inputs and outputs. in_channels and out_channels must both be divisible by groups. For example,
  - At groups=1, all inputs are convolved to all outputs.
  - At groups=2, the operation becomes equivalent to having two conv layers side by side, each seeing half the input channels, and producing half the output channels, and both subsequently concatenated.
  - At groups= in_channels, each input channel is convolved with its own set of filters (of size ⌊out_channelsin_channels⌋\left\lfloor\frac{out\_channels}{in\_channels}\right\rfloor⌊in_channelsout_channels⌋ ).
- in_channels (int) – Number of channels in the input image
- out_channels (int) – Number of channels produced by the convolution
- kernel_size (int or tuple) – Size of the convolving kernel
- stride (int or tuple, optional) – Stride of the convolution. Default: 1
- padding (int or tuple, optional) – dilation * (kernel_size - 1) - padding zero-padding will be added to both sides of the input. Default: 0
- output_padding (int or tuple, optional) – Additional size added to one side of the output shape. Default: 0
- groups (int, optional) – Number of blocked connections from input channels to output channels. Default: 1
- bias (bool, optional) – If True, adds a learnable bias to the output. Default: True
- dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1
- Input: (N,Cin,Lin)(N, C_{in}, L_{in})(N,Cin,Lin)
- Output: (N,Cout,Lout)(N, C_{out}, L_{out})(N,Cout,Lout) where
  
  Lout=(Lin−1)×stride−2×padding+dilation×(kernel_size−1)+output_padding+1L_{out} = (L_{in} - 1) \times \text{stride} - 2 \times \text{padding} + \text{dilation} \times (\text{kernel\_size} - 1) + \text{output\_padding} + 1 Lout=(Lin−1)×stride−2×padding+dilation×(kernel_size−1)+output_padding+1
- ~ConvTranspose1d.weight (Tensor) – the learnable weights of the module of shape (in_channels,out_channelsgroups,(\text{in\_channels}, \frac{\text{out\_channels}}{\text{groups}},(in_channels,groupsout_channels, kernel_size)\text{kernel\_size})kernel_size) . The values of these weights are sampled from U(−k,k)\mathcal{U}(-\sqrt{k}, \sqrt{k})U(−k
) where k=1Cin∗kernel_sizek = \frac{1}{C_\text{in} * \text{kernel\_size}}k=Cin∗kernel_size1
~ConvTranspose1d.bias (Tensor) – the learnable bias of the module of shape (out_channels). If bias is True, then the values of these weights are sampled from U(−k,k)\mathcal{U}(-\sqrt{k}, \sqrt{k})U(−k
,k
ConvTranspose2d

class torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode='zeros')[source]

Applies a 2D transposed convolution operator over an input image composed of several input planes.

This module can be seen as the gradient of Conv2d with respect to its input. It is also known as a fractionally-strided convolution or a deconvolution (although it is not an actual deconvolution operation).

The parameters kernel_size, stride, padding, output_padding can either be:
- a single int – in which case the same value is used for the height and width dimensions
- a tuple of two ints – in which case, the first int is used for the height dimension, and the second int for the width dimension
Note

Depending of the size of your kernel, several (of the last) columns of the input might be lost, because it is a valid cross-correlation, and not a full cross-correlation. It is up to the user to add proper padding.

Note

The padding argument effectively adds dilation * (kernel_size - 1) - padding amount of zero padding to both sizes of the input. This is set so that when a Conv2d and a ConvTranspose2d are initialized with same parameters, they are inverses of each other in regard to the input and output shapes. However, when stride > 1, Conv2d maps multiple input shapes to the same output shape. output_padding is provided to resolve this ambiguity by effectively increasing the calculated output shape on one side. Note that output_padding is only used to find output shape, but does not actually add zero-padding to output.

Note

In some circumstances when using the CUDA backend with CuDNN, this operator may select a nondeterministic algorithm to increase performance. If this is undesirable, you can try to make the operation deterministic (potentially at a performance cost) by setting torch.backends.cudnn.deterministic = True. Please see the notes on Reproducibility for background.

Parameters

Shape:

Hout=(Hin−1)×stride[0]−2×padding[0]+dilation[0]×(kernel_size[0]−1)+output_padding[0]+1H_{out} = (H_{in} - 1) \times \text{stride}[0] - 2 \times \text{padding}[0] + \text{dilation}[0] \times (\text{kernel\_size}[0] - 1) + \text{output\_padding}[0] + 1 Hout=(Hin−1)×stride[0]−2×padding[0]+dilation[0]×(kernel_size[0]−1)+output_padding[0]+1

Wout=(Win−1)×stride[1]−2×padding[1]+dilation[1]×(kernel_size[1]−1)+output_padding[1]+1W_{out} = (W_{in} - 1) \times \text{stride}[1] - 2 \times \text{padding}[1] + \text{dilation}[1] \times (\text{kernel\_size}[1] - 1) + \text{output\_padding}[1] + 1 Wout=(Win−1)×stride[1]−2×padding[1]+dilation[1]×(kernel_size[1]−1)+output_padding[1]+1

Variables
,k
- ) where k=1Cin∗kernel_sizek = \frac{1}{C_\text{in} * \text{kernel\_size}}k=Cin∗kernel_size1
- stride controls the stride for the cross-correlation.
- padding controls the amount of implicit zero-paddings on both sides for dilation * (kernel_size - 1) - padding number of points. See note below for details.
- output_padding controls the additional size added to one side of the output shape. See note below for details.
- dilation controls the spacing between the kernel points; also known as the à trous algorithm. It is harder to describe, but this link has a nice visualization of what dilation does.
- groups controls the connections between inputs and outputs. in_channels and out_channels must both be divisible by groups. For example,
  - At groups=1, all inputs are convolved to all outputs.
  - At groups=2, the operation becomes equivalent to having two conv layers side by side, each seeing half the input channels, and producing half the output channels, and both subsequently concatenated.
  - At groups= in_channels, each input channel is convolved with its own set of filters (of size ⌊out_channelsin_channels⌋\left\lfloor\frac{out\_channels}{in\_channels}\right\rfloor⌊in_channelsout_channels⌋ ).
- in_channels (int) – Number of channels in the input image
- out_channels (int) – Number of channels produced by the convolution
- kernel_size (int or tuple) – Size of the convolving kernel
- stride (int or tuple, optional) – Stride of the convolution. Default: 1
- padding (int or tuple, optional) – dilation * (kernel_size - 1) - padding zero-padding will be added to both sides of each dimension in the input. Default: 0
- output_padding (int or tuple, optional) – Additional size added to one side of each dimension in the output shape. Default: 0
- groups (int, optional) – Number of blocked connections from input channels to output channels. Default: 1
- bias (bool, optional) – If True, adds a learnable bias to the output. Default: True
- dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1
- Input: (N,Cin,Hin,Win)(N, C_{in}, H_{in}, W_{in})(N,Cin,Hin,Win)
- Output: (N,Cout,Hout,Wout)(N, C_{out}, H_{out}, W_{out})(N,Cout,Hout,Wout) where
- ~ConvTranspose2d.weight (Tensor) – the learnable weights of the module of shape (in_channels,out_channelsgroups,(\text{in\_channels}, \frac{\text{out\_channels}}{\text{groups}},(in_channels,groupsout_channels, kernel_size[0],kernel_size[1])\text{kernel\_size[0]}, \text{kernel\_size[1]})kernel_size[0],kernel_size[1]) . The values of these weights are sampled from U(−k,k)\mathcal{U}(-\sqrt{k}, \sqrt{k})U(−k
) where k=1Cin∗∏i=01kernel_size[i]k = \frac{1}{C_\text{in} * \prod_{i=0}^{1}\text{kernel\_size}[i]}k=Cin∗∏i=01kernel_size[i]1
~ConvTranspose2d.bias (Tensor) – the learnable bias of the module of shape (out_channels) If bias is True, then the values of these weights are sampled from U(−k,k)\mathcal{U}(-\sqrt{k}, \sqrt{k})U(−k
,k
Examples:
```
>>> # With square kernels and equal stride
>>> m = nn.ConvTranspose2d(16, 33, 3, stride=2)
>>> # non-square kernels and unequal stride and with padding
>>> m = nn.ConvTranspose2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2))
>>> input = torch.randn(20, 16, 50, 100)
>>> output = m(input)
>>> # exact output size can be also specified as an argument
>>> input = torch.randn(1, 16, 12, 12)
>>> downsample = nn.Conv2d(16, 16, 3, stride=2, padding=1)
>>> upsample = nn.ConvTranspose2d(16, 16, 3, stride=2, padding=1)
>>> h = downsample(input)
>>> h.size()
torch.Size([1, 16, 6, 6])
>>> output = upsample(h, output_size=input.size())
>>> output.size()
torch.Size([1, 16, 12, 12])
```
ConvTranspose3d

class torch.nn.ConvTranspose3d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode='zeros')[source]

Applies a 3D transposed convolution operator over an input image composed of several input planes. The transposed convolution operator multiplies each input value element-wise by a learnable kernel, and sums over the outputs from all input feature planes.

This module can be seen as the gradient of Conv3d with respect to its input. It is also known as a fractionally-strided convolution or a deconvolution (although it is not an actual deconvolution operation).

The parameters kernel_size, stride, padding, output_padding can either be:
- a single int – in which case the same value is used for the depth, height and width dimensions
- a tuple of three ints – in which case, the first int is used for the depth dimension, the second int for the height dimension and the third int for the width dimension
Note

Depending of the size of your kernel, several (of the last) columns of the input might be lost, because it is a valid cross-correlation, and not a full cross-correlation. It is up to the user to add proper padding.

Note

The padding argument effectively adds dilation * (kernel_size - 1) - padding amount of zero padding to both sizes of the input. This is set so that when a Conv3d and a ConvTranspose3d are initialized with same parameters, they are inverses of each other in regard to the input and output shapes. However, when stride > 1, Conv3d maps multiple input shapes to the same output shape. output_padding is provided to resolve this ambiguity by effectively increasing the calculated output shape on one side. Note that output_padding is only used to find output shape, but does not actually add zero-padding to output.

Note

In some circumstances when using the CUDA backend with CuDNN, this operator may select a nondeterministic algorithm to increase performance. If this is undesirable, you can try to make the operation deterministic (potentially at a performance cost) by setting torch.backends.cudnn.deterministic = True. Please see the notes on Reproducibility for background.

Parameters

Shape:

Dout=(Din−1)×stride[0]−2×padding[0]+dilation[0]×(kernel_size[0]−1)+output_padding[0]+1D_{out} = (D_{in} - 1) \times \text{stride}[0] - 2 \times \text{padding}[0] + \text{dilation}[0] \times (\text{kernel\_size}[0] - 1) + \text{output\_padding}[0] + 1 Dout=(Din−1)×stride[0]−2×padding[0]+dilation[0]×(kernel_size[0]−1)+output_padding[0]+1

Hout=(Hin−1)×stride[1]−2×padding[1]+dilation[1]×(kernel_size[1]−1)+output_padding[1]+1H_{out} = (H_{in} - 1) \times \text{stride}[1] - 2 \times \text{padding}[1] + \text{dilation}[1] \times (\text{kernel\_size}[1] - 1) + \text{output\_padding}[1] + 1 Hout=(Hin−1)×stride[1]−2×padding[1]+dilation[1]×(kernel_size[1]−1)+output_padding[1]+1

Wout=(Win−1)×stride[2]−2×padding[2]+dilation[2]×(kernel_size[2]−1)+output_padding[2]+1W_{out} = (W_{in} - 1) \times \text{stride}[2] - 2 \times \text{padding}[2] + \text{dilation}[2] \times (\text{kernel\_size}[2] - 1) + \text{output\_padding}[2] + 1 Wout=(Win−1)×stride[2]−2×padding[2]+dilation[2]×(kernel_size[2]−1)+output_padding[2]+1

Variables
,k
- ) where k=1Cin∗∏i=01kernel_size[i]k = \frac{1}{C_\text{in} * \prod_{i=0}^{1}\text{kernel\_size}[i]}k=Cin∗∏i=01kernel_size[i]1
- stride controls the stride for the cross-correlation.
- padding controls the amount of implicit zero-paddings on both sides for dilation * (kernel_size - 1) - padding number of points. See note below for details.
- output_padding controls the additional size added to one side of the output shape. See note below for details.
- dilation controls the spacing between the kernel points; also known as the à trous algorithm. It is harder to describe, but this link has a nice visualization of what dilation does.
- groups controls the connections between inputs and outputs. in_channels and out_channels must both be divisible by groups. For example,
  - At groups=1, all inputs are convolved to all outputs.
  - At groups=2, the operation becomes equivalent to having two conv layers side by side, each seeing half the input channels, and producing half the output channels, and both subsequently concatenated.
  - At groups= in_channels, each input channel is convolved with its own set of filters (of size ⌊out_channelsin_channels⌋\left\lfloor\frac{out\_channels}{in\_channels}\right\rfloor⌊in_channelsout_channels⌋ ).
- in_channels (int) – Number of channels in the input image
- out_channels (int) – Number of channels produced by the convolution
- kernel_size (int or tuple) – Size of the convolving kernel
- stride (int or tuple, optional) – Stride of the convolution. Default: 1
- padding (int or tuple, optional) – dilation * (kernel_size - 1) - padding zero-padding will be added to both sides of each dimension in the input. Default: 0
- output_padding (int or tuple, optional) – Additional size added to one side of each dimension in the output shape. Default: 0
- groups (int, optional) – Number of blocked connections from input channels to output channels. Default: 1
- bias (bool, optional) – If True, adds a learnable bias to the output. Default: True
- dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1
- Input: (N,Cin,Din,Hin,Win)(N, C_{in}, D_{in}, H_{in}, W_{in})(N,Cin,Din,Hin,Win)
- Output: (N,Cout,Dout,Hout,Wout)(N, C_{out}, D_{out}, H_{out}, W_{out})(N,Cout,Dout,Hout,Wout) where
- ~ConvTranspose3d.weight (Tensor) – the learnable weights of the module of shape (in_channels,out_channelsgroups,(\text{in\_channels}, \frac{\text{out\_channels}}{\text{groups}},(in_channels,groupsout_channels, kernel_size[0],kernel_size[1],kernel_size[2])\text{kernel\_size[0]}, \text{kernel\_size[1]}, \text{kernel\_size[2]})kernel_size[0],kernel_size[1],kernel_size[2]) . The values of these weights are sampled from U(−k,k)\mathcal{U}(-\sqrt{k}, \sqrt{k})U(−k
) where k=1Cin∗∏i=02kernel_size[i]k = \frac{1}{C_\text{in} * \prod_{i=0}^{2}\text{kernel\_size}[i]}k=Cin∗∏i=02kernel_size[i]1
~ConvTranspose3d.bias (Tensor) – the learnable bias of the module of shape (out_channels) If bias is True, then the values of these weights are sampled from U(−k,k)\mathcal{U}(-\sqrt{k}, \sqrt{k})U(−k
,k
Examples:
```
>>> # With square kernels and equal stride
>>> m = nn.ConvTranspose3d(16, 33, 3, stride=2)
>>> # non-square kernels and unequal stride and with padding
>>> m = nn.ConvTranspose3d(16, 33, (3, 5, 2), stride=(2, 1, 1), padding=(0, 4, 2))
>>> input = torch.randn(20, 16, 10, 50, 100)
>>> output = m(input)
```
Unfold

class torch.nn.Unfold(kernel_size, dilation=1, padding=0, stride=1)[source]

Extracts sliding local blocks from a batched input tensor.

Consider an batched input tensor of shape (N,C,∗)(N, C, *)(N,C,∗) , where NNN is the batch dimension, CCC is the channel dimension, and ∗*∗ represent arbitrary spatial dimensions. This operation flattens each sliding kernel_size-sized block within the spatial dimensions of input into a column (i.e., last dimension) of a 3-D output tensor of shape (N,C×∏(kernel_size),L)(N, C \times \prod(\text{kernel\_size}), L)(N,C×∏(kernel_size),L) , where C×∏(kernel_size)C \times \prod(\text{kernel\_size})C×∏(kernel_size) is the total number of values within each block (a block has ∏(kernel_size)\prod(\text{kernel\_size})∏(kernel_size) spatial locations each containing a CCC -channeled vector), and LLL is the total number of such blocks:

L=∏d⌊spatial_size[d]+2×padding[d]−dilation[d]×(kernel_size[d]−1)−1stride[d]+1⌋,L = \prod_d \left\lfloor\frac{\text{spatial\_size}[d] + 2 \times \text{padding}[d] % - \text{dilation}[d] \times (\text{kernel\_size}[d] - 1) - 1}{\text{stride}[d]} + 1\right\rfloor, L=d∏⌊stride[d]spatial_size[d]+2×padding[d]−dilation[d]×(kernel_size[d]−1)−1+1⌋,

where spatial_size\text{spatial\_size}spatial_size is formed by the spatial dimensions of input (∗*∗ above), and ddd is over all spatial dimensions.

Therefore, indexing output at the last dimension (column dimension) gives all values within a certain block.

The padding, stride and dilation arguments specify how the sliding blocks are retrieved.

Parameters

Note

Fold calculates each combined value in the resulting large tensor by summing all values from all containing blocks. Unfold extracts the values in the local blocks by copying from the large tensor. So, if the blocks overlap, they are not inverses of each other.

Warning

Currently, only 4-D input tensors (batched image-like tensors) are supported.

Shape:

Examples:
```
>>> unfold = nn.Unfold(kernel_size=(2, 3))
>>> input = torch.randn(2, 5, 3, 4)
>>> output = unfold(input)
>>> # each patch contains 30 values (2x3=6 vectors, each of 5 channels)
>>> # 4 blocks (2x3 kernels) in total in the 3x4 input
>>> output.size()
torch.Size([2, 30, 4])

>>> # Convolution is equivalent with Unfold + Matrix Multiplication + Fold (or view to output shape)
>>> inp = torch.randn(1, 3, 10, 12)
>>> w = torch.randn(2, 3, 4, 5)
>>> inp_unf = torch.nn.functional.unfold(inp, (4, 5))
>>> out_unf = inp_unf.transpose(1, 2).matmul(w.view(w.size(0), -1).t()).transpose(1, 2)
>>> out = torch.nn.functional.fold(out_unf, (7, 8), (1, 1))
>>> # or equivalently (and avoiding a copy),
>>> # out = out_unf.view(1, 2, 7, 8)
>>> (torch.nn.functional.conv2d(inp, w) - out).abs().max()
tensor(1.9073e-06)
```
Fold

class torch.nn.Fold(output_size, kernel_size, dilation=1, padding=0, stride=1)[source]

Combines an array of sliding local blocks into a large containing tensor.

Consider a batched input tensor containing sliding local blocks, e.g., patches of images, of shape (N,C×∏(kernel_size),L)(N, C \times \prod(\text{kernel\_size}), L)(N,C×∏(kernel_size),L) , where NNN is batch dimension, C×∏(kernel_size)C \times \prod(\text{kernel\_size})C×∏(kernel_size) is the number of values within a block (a block has ∏(kernel_size)\prod(\text{kernel\_size})∏(kernel_size) spatial locations each containing a CCC -channeled vector), and LLL is the total number of blocks. (This is exactly the same specification as the output shape of Unfold.) This operation combines these local blocks into the large output tensor of shape (N,C,output_size[0],output_size[1],… )(N, C, \text{output\_size}[0], \text{output\_size}[1], \dots)(N,C,output_size[0],output_size[1],…) by summing the overlapping values. Similar to Unfold, the arguments must satisfy

L=∏d⌊output_size[d]+2×padding[d]−dilation[d]×(kernel_size[d]−1)−1stride[d]+1⌋,L = \prod_d \left\lfloor\frac{\text{output\_size}[d] + 2 \times \text{padding}[d] % - \text{dilation}[d] \times (\text{kernel\_size}[d] - 1) - 1}{\text{stride}[d]} + 1\right\rfloor, L=d∏⌊stride[d]output_size[d]+2×padding[d]−dilation[d]×(kernel_size[d]−1)−1+1⌋,

where ddd is over all spatial dimensions.

The padding, stride and dilation arguments specify how the sliding blocks are retrieved.

Parameters

Note

Fold calculates each combined value in the resulting large tensor by summing all values from all containing blocks. Unfold extracts the values in the local blocks by copying from the large tensor. So, if the blocks overlap, they are not inverses of each other.

Warning

Currently, only 4-D output tensors (batched image-like tensors) are supported.

Shape:

Examples:
```
>>> fold = nn.Fold(output_size=(4, 5), kernel_size=(2, 2))
>>> input = torch.randn(1, 3 * 2 * 2, 12)
>>> output = fold(input)
>>> output.size()
torch.Size([1, 3, 4, 5])
```
Pooling layers

MaxPool1d

class torch.nn.MaxPool1d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)[source]

Applies a 1D max pooling over an input signal composed of several input planes.

In the simplest case, the output value of the layer with input size (N,C,L)(N, C, L)(N,C,L) and output (N,C,Lout)(N, C, L_{out})(N,C,Lout) can be precisely described as:

out(Ni,Cj,k)=max⁡m=0,…,kernel_size−1input(Ni,Cj,stride×k+m)out(N_i, C_j, k) = \max_{m=0, \ldots, \text{kernel\_size} - 1} input(N_i, C_j, stride \times k + m) out(Ni,Cj,k)=m=0,…,kernel_size−1maxinput(Ni,Cj,stride×k+m)

If padding is non-zero, then the input is implicitly zero-padded on both sides for padding number of points. dilation controls the spacing between the kernel points. It is harder to describe, but this link has a nice visualization of what dilation does.

Parameters

Shape:

Examples:
```
>>> # pool of size=3, stride=2
>>> m = nn.MaxPool1d(3, stride=2)
>>> input = torch.randn(20, 16, 50)
>>> output = m(input)
```
MaxPool2d

class torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)[source]

Applies a 2D max pooling over an input signal composed of several input planes.

In the simplest case, the output value of the layer with input size (N,C,H,W)(N, C, H, W)(N,C,H,W) , output (N,C,Hout,Wout)(N, C, H_{out}, W_{out})(N,C,Hout,Wout) and kernel_size (kH,kW)(kH, kW)(kH,kW) can be precisely described as:

out(Ni,Cj,h,w)=max⁡m=0,…,kH−1max⁡n=0,…,kW−1input(Ni,Cj,stride[0]×h+m,stride[1]×w+n)\begin{aligned} out(N_i, C_j, h, w) ={} & \max_{m=0, \ldots, kH-1} \max_{n=0, \ldots, kW-1} \\ & \text{input}(N_i, C_j, \text{stride[0]} \times h + m, \text{stride[1]} \times w + n) \end{aligned} out(Ni,Cj,h,w)=m=0,…,kH−1maxn=0,…,kW−1maxinput(Ni,Cj,stride[0]×h+m,stride[1]×w+n)

If padding is non-zero, then the input is implicitly zero-padded on both sides for padding number of points. dilation controls the spacing between the kernel points. It is harder to describe, but this link has a nice visualization of what dilation does.

The parameters kernel_size, stride, padding, dilation can either be:
- a single int – in which case the same value is used for the height and width dimension
- a tuple of two ints – in which case, the first int is used for the height dimension, and the second int for the width dimension
Parameters

Shape:

Examples:
```
>>> # pool of square window of size=3, stride=2
>>> m = nn.MaxPool2d(3, stride=2)
>>> # pool of non-square window
>>> m = nn.MaxPool2d((3, 2), stride=(2, 1))
>>> input = torch.randn(20, 16, 50, 32)
>>> output = m(input)
```
MaxPool3d

class torch.nn.MaxPool3d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)[source]

Applies a 3D max pooling over an input signal composed of several input planes.

In the simplest case, the output value of the layer with input size (N,C,D,H,W)(N, C, D, H, W)(N,C,D,H,W) , output (N,C,Dout,Hout,Wout)(N, C, D_{out}, H_{out}, W_{out})(N,C,Dout,Hout,Wout) and kernel_size (kD,kH,kW)(kD, kH, kW)(kD,kH,kW) can be precisely described as:

out(Ni,Cj,d,h,w)=max⁡k=0,…,kD−1max⁡m=0,…,kH−1max⁡n=0,…,kW−1input(Ni,Cj,stride[0]×d+k,stride[1]×h+m,stride[2]×w+n)\begin{aligned} \text{out}(N_i, C_j, d, h, w) ={} & \max_{k=0, \ldots, kD-1} \max_{m=0, \ldots, kH-1} \max_{n=0, \ldots, kW-1} \\ & \text{input}(N_i, C_j, \text{stride[0]} \times d + k, \text{stride[1]} \times h + m, \text{stride[2]} \times w + n) \end{aligned} out(Ni,Cj,d,h,w)=k=0,…,kD−1maxm=0,…,kH−1maxn=0,…,kW−1maxinput(Ni,Cj,stride[0]×d+k,stride[1]×h+m,stride[2]×w+n)

If padding is non-zero, then the input is implicitly zero-padded on both sides for padding number of points. dilation controls the spacing between the kernel points. It is harder to describe, but this link has a nice visualization of what dilation does.

The parameters kernel_size, stride, padding, dilation can either be:
- a single int – in which case the same value is used for the depth, height and width dimension
- a tuple of three ints – in which case, the first int is used for the depth dimension, the second int for the height dimension and the third int for the width dimension
Parameters

Shape:

Examples:
```
>>> # pool of square window of size=3, stride=2
>>> m = nn.MaxPool3d(3, stride=2)
>>> # pool of non-square window
>>> m = nn.MaxPool3d((3, 2, 2), stride=(2, 1, 2))
>>> input = torch.randn(20, 16, 50,44, 31)
>>> output = m(input)
```
MaxUnpool1d

class torch.nn.MaxUnpool1d(kernel_size, stride=None, padding=0)[source]

Computes a partial inverse of MaxPool1d.

MaxPool1d is not fully invertible, since the non-maximal values are lost.

MaxUnpool1d takes in as input the output of MaxPool1d including the indices of the maximal values and computes a partial inverse in which all non-maximal values are set to zero.

Note

MaxPool1d can map several input sizes to the same output sizes. Hence, the inversion process can get ambiguous. To accommodate this, you can provide the needed output size as an additional argument output_size in the forward call. See the Inputs and Example below.

Parameters

Inputs:

Shape:

Example:
```
>>> pool = nn.MaxPool1d(2, stride=2, return_indices=True)
>>> unpool = nn.MaxUnpool1d(2, stride=2)
>>> input = torch.tensor([[[1., 2, 3, 4, 5, 6, 7, 8]]])
>>> output, indices = pool(input)
>>> unpool(output, indices)
tensor([[[ 0.,  2.,  0.,  4.,  0.,  6.,  0., 8.]]])

>>> # Example showcasing the use of output_size
>>> input = torch.tensor([[[1., 2, 3, 4, 5, 6, 7, 8, 9]]])
>>> output, indices = pool(input)
>>> unpool(output, indices, output_size=input.size())
tensor([[[ 0.,  2.,  0.,  4.,  0.,  6.,  0., 8.,  0.]]])

>>> unpool(output, indices)
tensor([[[ 0.,  2.,  0.,  4.,  0.,  6.,  0., 8.]]])
```
MaxUnpool2d

class torch.nn.MaxUnpool2d(kernel_size, stride=None, padding=0)[source]

Computes a partial inverse of MaxPool2d.

MaxPool2d is not fully invertible, since the non-maximal values are lost.

MaxUnpool2d takes in as input the output of MaxPool2d including the indices of the maximal values and computes a partial inverse in which all non-maximal values are set to zero.

Note

MaxPool2d can map several input sizes to the same output sizes. Hence, the inversion process can get ambiguous. To accommodate this, you can provide the needed output size as an additional argument output_size in the forward call. See the Inputs and Example below.

Parameters

Inputs:

Shape:

Example:
```
>>> pool = nn.MaxPool2d(2, stride=2, return_indices=True)
>>> unpool = nn.MaxUnpool2d(2, stride=2)
>>> input = torch.tensor([[[[ 1.,  2,  3,  4],
                            [ 5,  6,  7,  8],
                            [ 9, 10, 11, 12],
                            [13, 14, 15, 16]]]])
>>> output, indices = pool(input)
>>> unpool(output, indices)
tensor([[[[  0.,   0.,   0.,   0.],
          [  0.,   6.,   0.,   8.],
          [  0.,   0.,   0.,   0.],
          [  0.,  14.,   0.,  16.]]]])

>>> # specify a different output size than input size
>>> unpool(output, indices, output_size=torch.Size([1, 1, 5, 5]))
tensor([[[[  0.,   0.,   0.,   0.,   0.],
          [  6.,   0.,   8.,   0.,   0.],
          [  0.,   0.,   0.,  14.,   0.],
          [ 16.,   0.,   0.,   0.,   0.],
          [  0.,   0.,   0.,   0.,   0.]]]])
```
MaxUnpool3d

class torch.nn.MaxUnpool3d(kernel_size, stride=None, padding=0)[source]

Computes a partial inverse of MaxPool3d.

MaxPool3d is not fully invertible, since the non-maximal values are lost. MaxUnpool3d takes in as input the output of MaxPool3d including the indices of the maximal values and computes a partial inverse in which all non-maximal values are set to zero.

Note

MaxPool3d can map several input sizes to the same output sizes. Hence, the inversion process can get ambiguous. To accommodate this, you can provide the needed output size as an additional argument output_size in the forward call. See the Inputs section below.

Parameters

Inputs:

Shape:

Example:
```
>>> # pool of square window of size=3, stride=2
>>> pool = nn.MaxPool3d(3, stride=2, return_indices=True)
>>> unpool = nn.MaxUnpool3d(3, stride=2)
>>> output, indices = pool(torch.randn(20, 16, 51, 33, 15))
>>> unpooled_output = unpool(output, indices)
>>> unpooled_output.size()
torch.Size([20, 16, 51, 33, 15])
```
AvgPool1d

class torch.nn.AvgPool1d(kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True)[source]

Applies a 1D average pooling over an input signal composed of several input planes.

In the simplest case, the output value of the layer with input size (N,C,L)(N, C, L)(N,C,L) , output (N,C,Lout)(N, C, L_{out})(N,C,Lout) and kernel_size kkk can be precisely described as:

out(Ni,Cj,l)=1k∑m=0k−1input(Ni,Cj,stride×l+m)\text{out}(N_i, C_j, l) = \frac{1}{k} \sum_{m=0}^{k-1} \text{input}(N_i, C_j, \text{stride} \times l + m)out(Ni,Cj,l)=k1m=0∑k−1input(Ni,Cj,stride×l+m)

If padding is non-zero, then the input is implicitly zero-padded on both sides for padding number of points.

The parameters kernel_size, stride, padding can each be an int or a one-element tuple.

Parameters

Shape:

Examples:
```
>>> # pool with window of size=3, stride=2
>>> m = nn.AvgPool1d(3, stride=2)
>>> m(torch.tensor([[[1.,2,3,4,5,6,7]]]))
tensor([[[ 2.,  4.,  6.]]])
```
AvgPool2d

class torch.nn.AvgPool2d(kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True, divisor_override=None)[source]

Applies a 2D average pooling over an input signal composed of several input planes.

In the simplest case, the output value of the layer with input size (N,C,H,W)(N, C, H, W)(N,C,H,W) , output (N,C,Hout,Wout)(N, C, H_{out}, W_{out})(N,C,Hout,Wout) and kernel_size (kH,kW)(kH, kW)(kH,kW) can be precisely described as:

out(Ni,Cj,h,w)=1kH∗kW∑m=0kH−1∑n=0kW−1input(Ni,Cj,stride[0]×h+m,stride[1]×w+n)out(N_i, C_j, h, w) = \frac{1}{kH * kW} \sum_{m=0}^{kH-1} \sum_{n=0}^{kW-1} input(N_i, C_j, stride[0] \times h + m, stride[1] \times w + n)out(Ni,Cj,h,w)=kH∗kW1m=0∑kH−1n=0∑kW−1input(Ni,Cj,stride[0]×h+m,stride[1]×w+n)

If padding is non-zero, then the input is implicitly zero-padded on both sides for padding number of points.

The parameters kernel_size, stride, padding can either be:
- a single int – in which case the same value is used for the height and width dimension
- a tuple of two ints – in which case, the first int is used for the height dimension, and the second int for the width dimension
Parameters

Shape:

Examples:
```
>>> # pool of square window of size=3, stride=2
>>> m = nn.AvgPool2d(3, stride=2)
>>> # pool of non-square window
>>> m = nn.AvgPool2d((3, 2), stride=(2, 1))
>>> input = torch.randn(20, 16, 50, 32)
>>> output = m(input)
```
AvgPool3d

class torch.nn.AvgPool3d(kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True, divisor_override=None)[source]

Applies a 3D average pooling over an input signal composed of several input planes.

In the simplest case, the output value of the layer with input size (N,C,D,H,W)(N, C, D, H, W)(N,C,D,H,W) , output (N,C,Dout,Hout,Wout)(N, C, D_{out}, H_{out}, W_{out})(N,C,Dout,Hout,Wout) and kernel_size (kD,kH,kW)(kD, kH, kW)(kD,kH,kW) can be precisely described as:

out(Ni,Cj,d,h,w)=∑k=0kD−1∑m=0kH−1∑n=0kW−1input(Ni,Cj,stride[0]×d+k,stride[1]×h+m,stride[2]×w+n)kD×kH×kW\begin{aligned} \text{out}(N_i, C_j, d, h, w) ={} & \sum_{k=0}^{kD-1} \sum_{m=0}^{kH-1} \sum_{n=0}^{kW-1} \\ & \frac{\text{input}(N_i, C_j, \text{stride}[0] \times d + k, \text{stride}[1] \times h + m, \text{stride}[2] \times w + n)} {kD \times kH \times kW} \end{aligned} out(Ni,Cj,d,h,w)=k=0∑kD−1m=0∑kH−1n=0∑kW−1kD×kH×kWinput(Ni,Cj,stride[0]×d+k,stride[1]×h+m,stride[2]×w+n)

If padding is non-zero, then the input is implicitly zero-padded on all three sides for padding number of points.

The parameters kernel_size, stride can either be:
- a single int – in which case the same value is used for the depth, height and width dimension
- a tuple of three ints – in which case, the first int is used for the depth dimension, the second int for the height dimension and the third int for the width dimension
Parameters

Shape:

Examples:
```
>>> # pool of square window of size=3, stride=2
>>> m = nn.AvgPool3d(3, stride=2)
>>> # pool of non-square window
>>> m = nn.AvgPool3d((3, 2, 2), stride=(2, 1, 2))
>>> input = torch.randn(20, 16, 50,44, 31)
>>> output = m(input)
```
FractionalMaxPool2d

class torch.nn.FractionalMaxPool2d(kernel_size, output_size=None, output_ratio=None, return_indices=False, _random_samples=None)[source]

Applies a 2D fractional max pooling over an input signal composed of several input planes.

Fractional MaxPooling is described in detail in the paper Fractional MaxPooling by Ben Graham

The max-pooling operation is applied in kH×kWkH \times kWkH×kW regions by a stochastic step size determined by the target output size. The number of output features is equal to the number of input planes.

Parameters

Examples
```
>>> # pool of square window of size=3, and target output size 13x12
>>> m = nn.FractionalMaxPool2d(3, output_size=(13, 12))
>>> # pool of square window and target output size being half of input image size
>>> m = nn.FractionalMaxPool2d(3, output_ratio=(0.5, 0.5))
>>> input = torch.randn(20, 16, 50, 32)
>>> output = m(input)
```
LPPool1d

class torch.nn.LPPool1d(norm_type, kernel_size, stride=None, ceil_mode=False)[source]

Applies a 1D power-average pooling over an input signal composed of several input planes.

On each window, the function computed is:

f(X)=∑x∈Xxppf(X) = \sqrt[p]{\sum_{x \in X} x^{p}} f(X)=px∈X∑xp

Note

If the sum to the power of p is zero, the gradient of this function is not defined. This implementation will set the gradient to zero in this case.

Parameters

Shape:

Examples::
```
>>> # power-2 pool of window of length 3, with stride 2.
>>> m = nn.LPPool1d(2, 3, stride=2)
>>> input = torch.randn(20, 16, 50)
>>> output = m(input)
```
LPPool2d

class torch.nn.LPPool2d(norm_type, kernel_size, stride=None, ceil_mode=False)[source]

Applies a 2D power-average pooling over an input signal composed of several input planes.

On each window, the function computed is:

f(X)=∑x∈Xxppf(X) = \sqrt[p]{\sum_{x \in X} x^{p}} f(X)=px∈X∑xp

The parameters kernel_size, stride can either be:
- a single int – in which case the same value is used for the height and width dimension
- a tuple of two ints – in which case, the first int is used for the height dimension, and the second int for the width dimension
Note

If the sum to the power of p is zero, the gradient of this function is not defined. This implementation will set the gradient to zero in this case.

Parameters

Shape:

Examples:
```
>>> # power-2 pool of square window of size=3, stride=2
>>> m = nn.LPPool2d(2, 3, stride=2)
>>> # pool of non-square window of power 1.2
>>> m = nn.LPPool2d(1.2, (3, 2), stride=(2, 1))
>>> input = torch.randn(20, 16, 50, 32)
>>> output = m(input)
```
AdaptiveMaxPool1d

class torch.nn.AdaptiveMaxPool1d(output_size, return_indices=False)[source]

Applies a 1D adaptive max pooling over an input signal composed of several input planes.

The output size is H, for any input size. The number of output features is equal to the number of input planes.

Parameters

Examples
```
>>> # target output size of 5
>>> m = nn.AdaptiveMaxPool1d(5)
>>> input = torch.randn(1, 64, 8)
>>> output = m(input)
```
AdaptiveMaxPool2d

class torch.nn.AdaptiveMaxPool2d(output_size, return_indices=False)[source]

Applies a 2D adaptive max pooling over an input signal composed of several input planes.

The output is of size H x W, for any input size. The number of output features is equal to the number of input planes.

Parameters

Examples
```
>>> # target output size of 5x7
>>> m = nn.AdaptiveMaxPool2d((5,7))
>>> input = torch.randn(1, 64, 8, 9)
>>> output = m(input)
>>> # target output size of 7x7 (square)
>>> m = nn.AdaptiveMaxPool2d(7)
>>> input = torch.randn(1, 64, 10, 9)
>>> output = m(input)
>>> # target output size of 10x7
>>> m = nn.AdaptiveMaxPool2d((None, 7))
>>> input = torch.randn(1, 64, 10, 9)
>>> output = m(input)
```
AdaptiveMaxPool3d

class torch.nn.AdaptiveMaxPool3d(output_size, return_indices=False)[source]

Applies a 3D adaptive max pooling over an input signal composed of several input planes.

The output is of size D x H x W, for any input size. The number of output features is equal to the number of input planes.

Parameters

Examples
```
>>> # target output size of 5x7x9
>>> m = nn.AdaptiveMaxPool3d((5,7,9))
>>> input = torch.randn(1, 64, 8, 9, 10)
>>> output = m(input)
>>> # target output size of 7x7x7 (cube)
>>> m = nn.AdaptiveMaxPool3d(7)
>>> input = torch.randn(1, 64, 10, 9, 8)
>>> output = m(input)
>>> # target output size of 7x9x8
>>> m = nn.AdaptiveMaxPool3d((7, None, None))
>>> input = torch.randn(1, 64, 10, 9, 8)
>>> output = m(input)
```
AdaptiveAvgPool1d

class torch.nn.AdaptiveAvgPool1d(output_size)[source]

Applies a 1D adaptive average pooling over an input signal composed of several input planes.

The output size is H, for any input size. The number of output features is equal to the number of input planes.

Parameters

output_size – the target output size H

Examples
```
>>> # target output size of 5
>>> m = nn.AdaptiveAvgPool1d(5)
>>> input = torch.randn(1, 64, 8)
>>> output = m(input)
```
AdaptiveAvgPool2d

class torch.nn.AdaptiveAvgPool2d(output_size)[source]

Applies a 2D adaptive average pooling over an input signal composed of several input planes.

The output is of size H x W, for any input size. The number of output features is equal to the number of input planes.

Parameters

output_size – the target output size of the image of the form H x W. Can be a tuple (H, W) or a single H for a square image H x H. H and W can be either a int, or None which means the size will be the same as that of the input.

Examples
```
>>> # target output size of 5x7
>>> m = nn.AdaptiveAvgPool2d((5,7))
>>> input = torch.randn(1, 64, 8, 9)
>>> output = m(input)
>>> # target output size of 7x7 (square)
>>> m = nn.AdaptiveAvgPool2d(7)
>>> input = torch.randn(1, 64, 10, 9)
>>> output = m(input)
>>> # target output size of 10x7
>>> m = nn.AdaptiveMaxPool2d((None, 7))
>>> input = torch.randn(1, 64, 10, 9)
>>> output = m(input)
```
AdaptiveAvgPool3d

class torch.nn.AdaptiveAvgPool3d(output_size)[source]

Applies a 3D adaptive average pooling over an input signal composed of several input planes.

The output is of size D x H x W, for any input size. The number of output features is equal to the number of input planes.

Parameters

output_size – the target output size of the form D x H x W. Can be a tuple (D, H, W) or a single number D for a cube D x D x D. D, H and W can be either a int, or None which means the size will be the same as that of the input.

Examples
```
>>> # target output size of 5x7x9
>>> m = nn.AdaptiveAvgPool3d((5,7,9))
>>> input = torch.randn(1, 64, 8, 9, 10)
>>> output = m(input)
>>> # target output size of 7x7x7 (cube)
>>> m = nn.AdaptiveAvgPool3d(7)
>>> input = torch.randn(1, 64, 10, 9, 8)
>>> output = m(input)
>>> # target output size of 7x9x8
>>> m = nn.AdaptiveMaxPool3d((7, None, None))
>>> input = torch.randn(1, 64, 10, 9, 8)
>>> output = m(input)
```
Padding layers

ReflectionPad1d

class torch.nn.ReflectionPad1d(padding)[source]

Pads the input tensor using the reflection of the input boundary.

For N-dimensional padding, use torch.nn.functional.pad().

Parameters

padding (int, tuple) – the size of the padding. If is int, uses the same padding in all boundaries. If a 2-tuple, uses (padding_left\text{padding\_left}padding_left , padding_right\text{padding\_right}padding_right )

Shape:

Examples:
```
>>> m = nn.ReflectionPad1d(2)
>>> input = torch.arange(8, dtype=torch.float).reshape(1, 2, 4)
>>> input
tensor([[[0., 1., 2., 3.],
         [4., 5., 6., 7.]]])
>>> m(input)
tensor([[[2., 1., 0., 1., 2., 3., 2., 1.],
         [6., 5., 4., 5., 6., 7., 6., 5.]]])
>>> # using different paddings for different sides
>>> m = nn.ReflectionPad1d((3, 1))
>>> m(input)
tensor([[[3., 2., 1., 0., 1., 2., 3., 2.],
         [7., 6., 5., 4., 5., 6., 7., 6.]]])
```
ReflectionPad2d

class torch.nn.ReflectionPad2d(padding)[source]

Pads the input tensor using the reflection of the input boundary.

For N-dimensional padding, use torch.nn.functional.pad().

Parameters

padding (int, tuple) – the size of the padding. If is int, uses the same padding in all boundaries. If a 4-tuple, uses (padding_left\text{padding\_left}padding_left , padding_right\text{padding\_right}padding_right , padding_top\text{padding\_top}padding_top , padding_bottom\text{padding\_bottom}padding_bottom )

Shape:

Examples:
```
>>> m = nn.ReflectionPad2d(2)
>>> input = torch.arange(9, dtype=torch.float).reshape(1, 1, 3, 3)
>>> input
tensor([[[[0., 1., 2.],
          [3., 4., 5.],
          [6., 7., 8.]]]])
>>> m(input)
tensor([[[[8., 7., 6., 7., 8., 7., 6.],
          [5., 4., 3., 4., 5., 4., 3.],
          [2., 1., 0., 1., 2., 1., 0.],
          [5., 4., 3., 4., 5., 4., 3.],
          [8., 7., 6., 7., 8., 7., 6.],
          [5., 4., 3., 4., 5., 4., 3.],
          [2., 1., 0., 1., 2., 1., 0.]]]])
>>> # using different paddings for different sides
>>> m = nn.ReflectionPad2d((1, 1, 2, 0))
>>> m(input)
tensor([[[[7., 6., 7., 8., 7.],
          [4., 3., 4., 5., 4.],
          [1., 0., 1., 2., 1.],
          [4., 3., 4., 5., 4.],
          [7., 6., 7., 8., 7.]]]])
```
ReplicationPad1d

class torch.nn.ReplicationPad1d(padding)[source]

Pads the input tensor using replication of the input boundary.

For N-dimensional padding, use torch.nn.functional.pad().

Parameters

padding (int, tuple) – the size of the padding. If is int, uses the same padding in all boundaries. If a 2-tuple, uses (padding_left\text{padding\_left}padding_left , padding_right\text{padding\_right}padding_right )

Shape:

Examples:
```
>>> m = nn.ReplicationPad1d(2)
>>> input = torch.arange(8, dtype=torch.float).reshape(1, 2, 4)
>>> input
tensor([[[0., 1., 2., 3.],
         [4., 5., 6., 7.]]])
>>> m(input)
tensor([[[0., 0., 0., 1., 2., 3., 3., 3.],
         [4., 4., 4., 5., 6., 7., 7., 7.]]])
>>> # using different paddings for different sides
>>> m = nn.ReplicationPad1d((3, 1))
>>> m(input)
tensor([[[0., 0., 0., 0., 1., 2., 3., 3.],
         [4., 4., 4., 4., 5., 6., 7., 7.]]])
```
ReplicationPad2d

class torch.nn.ReplicationPad2d(padding)[source]

Pads the input tensor using replication of the input boundary.

For N-dimensional padding, use torch.nn.functional.pad().

Parameters

padding (int, tuple) – the size of the padding. If is int, uses the same padding in all boundaries. If a 4-tuple, uses (padding_left\text{padding\_left}padding_left , padding_right\text{padding\_right}padding_right , padding_top\text{padding\_top}padding_top , padding_bottom\text{padding\_bottom}padding_bottom )

Shape:

Examples:
```
>>> m = nn.ReplicationPad2d(2)
>>> input = torch.arange(9, dtype=torch.float).reshape(1, 1, 3, 3)
>>> input
tensor([[[[0., 1., 2.],
          [3., 4., 5.],
          [6., 7., 8.]]]])
>>> m(input)
tensor([[[[0., 0., 0., 1., 2., 2., 2.],
          [0., 0., 0., 1., 2., 2., 2.],
          [0., 0., 0., 1., 2., 2., 2.],
          [3., 3., 3., 4., 5., 5., 5.],
          [6., 6., 6., 7., 8., 8., 8.],
          [6., 6., 6., 7., 8., 8., 8.],
          [6., 6., 6., 7., 8., 8., 8.]]]])
>>> # using different paddings for different sides
>>> m = nn.ReplicationPad2d((1, 1, 2, 0))
>>> m(input)
tensor([[[[0., 0., 1., 2., 2.],
          [0., 0., 1., 2., 2.],
          [0., 0., 1., 2., 2.],
          [3., 3., 4., 5., 5.],
          [6., 6., 7., 8., 8.]]]])
```
ReplicationPad3d

class torch.nn.ReplicationPad3d(padding)[source]

Pads the input tensor using replication of the input boundary.

For N-dimensional padding, use torch.nn.functional.pad().

Parameters

padding (int, tuple) – the size of the padding. If is int, uses the same padding in all boundaries. If a 6-tuple, uses (padding_left\text{padding\_left}padding_left , padding_right\text{padding\_right}padding_right , padding_top\text{padding\_top}padding_top , padding_bottom\text{padding\_bottom}padding_bottom , padding_front\text{padding\_front}padding_front , padding_back\text{padding\_back}padding_back )

Shape:

Examples:
```
>>> m = nn.ReplicationPad3d(3)
>>> input = torch.randn(16, 3, 8, 320, 480)
>>> output = m(input)
>>> # using different paddings for different sides
>>> m = nn.ReplicationPad3d((3, 3, 6, 6, 1, 1))
>>> output = m(input)
```
ZeroPad2d

class torch.nn.ZeroPad2d(padding)[source]

Pads the input tensor boundaries with zero.

For N-dimensional padding, use torch.nn.functional.pad().

Parameters

padding (int, tuple) – the size of the padding. If is int, uses the same padding in all boundaries. If a 4-tuple, uses (padding_left\text{padding\_left}padding_left , padding_right\text{padding\_right}padding_right , padding_top\text{padding\_top}padding_top , padding_bottom\text{padding\_bottom}padding_bottom )

Shape:

Examples:
```
>>> m = nn.ZeroPad2d(2)
>>> input = torch.randn(1, 1, 3, 3)
>>> input
tensor([[[[-0.1678, -0.4418,  1.9466],
          [ 0.9604, -0.4219, -0.5241],
          [-0.9162, -0.5436, -0.6446]]]])
>>> m(input)
tensor([[[[ 0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000],
          [ 0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000],
          [ 0.0000,  0.0000, -0.1678, -0.4418,  1.9466,  0.0000,  0.0000],
          [ 0.0000,  0.0000,  0.9604, -0.4219, -0.5241,  0.0000,  0.0000],
          [ 0.0000,  0.0000, -0.9162, -0.5436, -0.6446,  0.0000,  0.0000],
          [ 0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000],
          [ 0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000]]]])
>>> # using different paddings for different sides
>>> m = nn.ZeroPad2d((1, 1, 2, 0))
>>> m(input)
tensor([[[[ 0.0000,  0.0000,  0.0000,  0.0000,  0.0000],
          [ 0.0000,  0.0000,  0.0000,  0.0000,  0.0000],
          [ 0.0000, -0.1678, -0.4418,  1.9466,  0.0000],
          [ 0.0000,  0.9604, -0.4219, -0.5241,  0.0000],
          [ 0.0000, -0.9162, -0.5436, -0.6446,  0.0000]]]])
```
ConstantPad1d

class torch.nn.ConstantPad1d(padding, value)[source]

Pads the input tensor boundaries with a constant value.

For N-dimensional padding, use torch.nn.functional.pad().

Parameters

padding (int, tuple) – the size of the padding. If is int, uses the same padding in both boundaries. If a 2-tuple, uses (padding_left\text{padding\_left}padding_left , padding_right\text{padding\_right}padding_right )

Shape:

Examples:
```
>>> m = nn.ConstantPad1d(2, 3.5)
>>> input = torch.randn(1, 2, 4)
>>> input
tensor([[[-1.0491, -0.7152, -0.0749,  0.8530],
         [-1.3287,  1.8966,  0.1466, -0.2771]]])
>>> m(input)
tensor([[[ 3.5000,  3.5000, -1.0491, -0.7152, -0.0749,  0.8530,  3.5000,
           3.5000],
         [ 3.5000,  3.5000, -1.3287,  1.8966,  0.1466, -0.2771,  3.5000,
           3.5000]]])
>>> m = nn.ConstantPad1d(2, 3.5)
>>> input = torch.randn(1, 2, 3)
>>> input
tensor([[[ 1.6616,  1.4523, -1.1255],
         [-3.6372,  0.1182, -1.8652]]])
>>> m(input)
tensor([[[ 3.5000,  3.5000,  1.6616,  1.4523, -1.1255,  3.5000,  3.5000],
         [ 3.5000,  3.5000, -3.6372,  0.1182, -1.8652,  3.5000,  3.5000]]])
>>> # using different paddings for different sides
>>> m = nn.ConstantPad1d((3, 1), 3.5)
>>> m(input)
tensor([[[ 3.5000,  3.5000,  3.5000,  1.6616,  1.4523, -1.1255,  3.5000],
         [ 3.5000,  3.5000,  3.5000, -3.6372,  0.1182, -1.8652,  3.5000]]])
```
ConstantPad2d

class torch.nn.ConstantPad2d(padding, value)[source]

Pads the input tensor boundaries with a constant value.

For N-dimensional padding, use torch.nn.functional.pad().

Parameters

padding (int, tuple) – the size of the padding. If is int, uses the same padding in all boundaries. If a 4-tuple, uses (padding_left\text{padding\_left}padding_left , padding_right\text{padding\_right}padding_right , padding_top\text{padding\_top}padding_top , padding_bottom\text{padding\_bottom}padding_bottom )

Shape:

Examples:
```
>>> m = nn.ConstantPad2d(2, 3.5)
>>> input = torch.randn(1, 2, 2)
>>> input
tensor([[[ 1.6585,  0.4320],
         [-0.8701, -0.4649]]])
>>> m(input)
tensor([[[ 3.5000,  3.5000,  3.5000,  3.5000,  3.5000,  3.5000],
         [ 3.5000,  3.5000,  3.5000,  3.5000,  3.5000,  3.5000],
         [ 3.5000,  3.5000,  1.6585,  0.4320,  3.5000,  3.5000],
         [ 3.5000,  3.5000, -0.8701, -0.4649,  3.5000,  3.5000],
         [ 3.5000,  3.5000,  3.5000,  3.5000,  3.5000,  3.5000],
         [ 3.5000,  3.5000,  3.5000,  3.5000,  3.5000,  3.5000]]])
>>> # using different paddings for different sides
>>> m = nn.ConstantPad2d((3, 0, 2, 1), 3.5)
>>> m(input)
tensor([[[ 3.5000,  3.5000,  3.5000,  3.5000,  3.5000],
         [ 3.5000,  3.5000,  3.5000,  3.5000,  3.5000],
         [ 3.5000,  3.5000,  3.5000,  1.6585,  0.4320],
         [ 3.5000,  3.5000,  3.5000, -0.8701, -0.4649],
         [ 3.5000,  3.5000,  3.5000,  3.5000,  3.5000]]])
```
ConstantPad3d

class torch.nn.ConstantPad3d(padding, value)[source]

Pads the input tensor boundaries with a constant value.

For N-dimensional padding, use torch.nn.functional.pad().

Parameters

padding (int, tuple) – the size of the padding. If is int, uses the same padding in all boundaries. If a 6-tuple, uses (padding_left\text{padding\_left}padding_left , padding_right\text{padding\_right}padding_right , padding_top\text{padding\_top}padding_top , padding_bottom\text{padding\_bottom}padding_bottom , padding_front\text{padding\_front}padding_front , padding_back\text{padding\_back}padding_back )

Shape:

Examples:
```
>>> m = nn.ConstantPad3d(3, 3.5)
>>> input = torch.randn(16, 3, 10, 20, 30)
>>> output = m(input)
>>> # using different paddings for different sides
>>> m = nn.ConstantPad3d((3, 3, 6, 6, 0, 1), 3.5)
>>> output = m(input)
```
Non-linear activations (weighted sum, nonlinearity)

ELU

class torch.nn.ELU(alpha=1.0, inplace=False)[source]

Applies the element-wise function:

ELU(x)=max⁡(0,x)+min⁡(0,α∗(exp⁡(x)−1))\text{ELU}(x) = \max(0,x) + \min(0, \alpha * (\exp(x) - 1)) ELU(x)=max(0,x)+min(0,α∗(exp(x)−1))

Parameters
alpha – the α\alphaα value for the ELU formulation. Default: 1.0
inplace – can optionally do the operation in-place. Default: False

Shape

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.ELU()
>>> input = torch.randn(2)
>>> output = m(input)

Hardshrink

class torch.nn.Hardshrink(lambd=0.5)[source]

Applies the hard shrinkage function element-wise:

HardShrink(x)={x, if x>λx, if x<−λ0, otherwise \text{HardShrink}(x) = \begin{cases} x, & \text{ if } x > \lambda \\ x, & \text{ if } x < -\lambda \\ 0, & \text{ otherwise } \end{cases} HardShrink(x)=⎩⎪⎨⎪⎧x,x,0, if x>λ if x<−λ otherwise

Parameters

lambd – the λ\lambdaλ value for the Hardshrink formulation. Default: 0.5

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.Hardshrink()
>>> input = torch.randn(2)
>>> output = m(input)

Hardtanh

class torch.nn.Hardtanh(min_val=-1.0, max_val=1.0, inplace=False, min_value=None, max_value=None)[source]

Applies the HardTanh function element-wise

HardTanh is defined as:

HardTanh(x)={1 if x>1−1 if x<−1x otherwise \text{HardTanh}(x) = \begin{cases} 1 & \text{ if } x > 1 \\ -1 & \text{ if } x < -1 \\ x & \text{ otherwise } \\ \end{cases} HardTanh(x)=⎩⎪⎨⎪⎧1−1x if x>1 if x<−1 otherwise

The range of the linear region [−1,1][-1, 1][−1,1] can be adjusted using min_val and max_val.

Parameters

Keyword arguments min_value and max_value have been deprecated in favor of min_val and max_val.

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.Hardtanh(-2, 2)
>>> input = torch.randn(2)
>>> output = m(input)

LeakyReLU

class torch.nn.LeakyReLU(negative_slope=0.01, inplace=False)[source]

Applies the element-wise function:

LeakyReLU(x)=max⁡(0,x)+negative_slope∗min⁡(0,x)\text{LeakyReLU}(x) = \max(0, x) + \text{negative\_slope} * \min(0, x) LeakyReLU(x)=max(0,x)+negative_slope∗min(0,x)

LeakyRELU(x)={x, if x≥0negative_slope×x, otherwise \text{LeakyRELU}(x) = \begin{cases} x, & \text{ if } x \geq 0 \\ \text{negative\_slope} \times x, & \text{ otherwise } \end{cases} LeakyRELU(x)={x,negative_slope×x, if x≥0 otherwise

Parameters

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.LeakyReLU(0.1)
>>> input = torch.randn(2)
>>> output = m(input)

LogSigmoid

class torch.nn.LogSigmoid[source]

Applies the element-wise function:

LogSigmoid(x)=log⁡(11+exp⁡(−x))\text{LogSigmoid}(x) = \log\left(\frac{ 1 }{ 1 + \exp(-x)}\right) LogSigmoid(x)=log(1+exp(−x)1)

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.LogSigmoid()
>>> input = torch.randn(2)
>>> output = m(input)

MultiheadAttention

class torch.nn.MultiheadAttention(embed_dim, num_heads, dropout=0.0, bias=True, add_bias_kv=False, add_zero_attn=False, kdim=None, vdim=None)[source]

Allows the model to jointly attend to information from different representation subspaces. See reference: Attention Is All You Need

MultiHead(Q,K,V)=Concat(head1,…,headh)WOwhereheadi=Attention(QWiQ,KWiK,VWiV)\text{MultiHead}(Q, K, V) = \text{Concat}(head_1,\dots,head_h)W^O \text{where} head_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V) MultiHead(Q,K,V)=Concat(head1,…,headh)WOwhereheadi=Attention(QWiQ,KWiK,VWiV)

Parameters

embed_dim – total dimension of the model.
num_heads – parallel attention heads.
dropout – a Dropout layer on attn_output_weights. Default: 0.0.
bias – add bias as module parameter. Default: True.
add_bias_kv – add bias to the key and value sequences at dim=0.
add_zero_attn – add a new batch of zeros to the key and value sequences at dim=1.
kdim – total number of features in key. Default: None.
vdim – total number of features in key. Default: None.
Note – if kdim and vdim are None, they will be set to embed_dim such that
key, and value have the same number of features. (query,) –

Examples:

>>> multihead_attn = nn.MultiheadAttention(embed_dim, num_heads)
>>> attn_output, attn_output_weights = multihead_attn(query, key, value)

forward(query, key, value, key_padding_mask=None, need_weights=True, attn_mask=None)[source]

Parameters:

key, value (query,) – map a query and a set of key-value pairs to an output. See “Attention Is All You Need” for more details.
key_padding_mask – if provided, specified padding elements in the key will be ignored by the attention. This is an binary mask. When the value is True, the corresponding value on the attention layer will be filled with -inf.
need_weights – output attn_output_weights.
attn_mask – mask that prevents attention to certain positions. This is an additive mask (i.e. the values will be added to the attention layer).

Shape:

Inputs:
query: (L,N,E)(L, N, E)(L,N,E) where L is the target sequence length, N is the batch size, E is the embedding dimension.
key: (S,N,E)(S, N, E)(S,N,E) , where S is the source sequence length, N is the batch size, E is the embedding dimension.
value: (S,N,E)(S, N, E)(S,N,E) where S is the source sequence length, N is the batch size, E is the embedding dimension.
key_padding_mask: (N,S)(N, S)(N,S) , ByteTensor, where N is the batch size, S is the source sequence length.
attn_mask: (L,S)(L, S)(L,S) where L is the target sequence length, S is the source sequence length.
Outputs:
attn_output: (L,N,E)(L, N, E)(L,N,E) where L is the target sequence length, N is the batch size, E is the embedding dimension.
attn_output_weights: (N,L,S)(N, L, S)(N,L,S) where N is the batch size, L is the target sequence length, S is the source sequence length.

PReLU

class torch.nn.PReLU(num_parameters=1, init=0.25)[source]

Applies the element-wise function:

PReLU(x)=max⁡(0,x)+a∗min⁡(0,x)\text{PReLU}(x) = \max(0,x) + a * \min(0,x) PReLU(x)=max(0,x)+a∗min(0,x)

PReLU(x)={x, if x≥0ax, otherwise \text{PReLU}(x) = \begin{cases} x, & \text{ if } x \geq 0 \\ ax, & \text{ otherwise } \end{cases} PReLU(x)={x,ax, if x≥0 otherwise

Here aaa is a learnable parameter. When called without arguments, nn.PReLU() uses a single parameter aaa across all input channels. If called with nn.PReLU(nChannels), a separate aaa is used for each input channel.

Note

weight decay should not be used when learning aaa for good performance.

Note

Channel dim is the 2nd dim of input. When input has dims < 2, then there is no channel dim and the number of channels = 1.

Parameters

num_parameters (int) – number of aaa to learn. Although it takes an int as input, there is only two values are legitimate: 1, or the number of channels at input. Default: 1
init (float) – the initial value of aaa . Default: 0.25

Shape

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Variables

~PReLU.weight (Tensor) – the learnable weights of shape (num_parameters).

Examples:

>>> m = nn.PReLU()
>>> input = torch.randn(2)
>>> output = m(input)

ReLU

class torch.nn.ReLU(inplace=False)[source]

Applies the rectified linear unit function element-wise:

ReLU(x)=max⁡(0,x)\text{ReLU}(x)= \max(0, x)ReLU(x)=max(0,x)

Parameters

inplace – can optionally do the operation in-place. Default: False

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

  >>> m = nn.ReLU()
  >>> input = torch.randn(2)
  >>> output = m(input)


An implementation of CReLU - https://arxiv.org/abs/1603.05201

  >>> m = nn.ReLU()
  >>> input = torch.randn(2).unsqueeze(0)
  >>> output = torch.cat((m(input),m(-input)))

ReLU6

class torch.nn.ReLU6(inplace=False)[source]

Applies the element-wise function:

ReLU6(x)=min⁡(max⁡(0,x),6)\text{ReLU6}(x) = \min(\max(0,x), 6) ReLU6(x)=min(max(0,x),6)

Parameters

inplace – can optionally do the operation in-place. Default: False

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.ReLU6()
>>> input = torch.randn(2)
>>> output = m(input)

RReLU

class torch.nn.RReLU(lower=0.125, upper=0.3333333333333333, inplace=False)[source]

Applies the randomized leaky rectified liner unit function, element-wise, as described in the paper:

Empirical Evaluation of Rectified Activations in Convolutional Network.

The function is defined as:

RReLU(x)={xif x≥0ax otherwise \text{RReLU}(x) = \begin{cases} x & \text{if } x \geq 0 \\ ax & \text{ otherwise } \end{cases} RReLU(x)={xaxif x≥0 otherwise

where aaa is randomly sampled from uniform distribution U(lower,upper)\mathcal{U}(\text{lower}, \text{upper})U(lower,upper) .

See: https://arxiv.org/pdf/1505.00853.pdf

Parameters

Shape:

Examples:

>>> m = nn.RReLU(0.1, 0.3)
>>> input = torch.randn(2)
>>> output = m(input)

SELU

class torch.nn.SELU(inplace=False)[source]

Applied element-wise, as:

SELU(x)=scale∗(max⁡(0,x)+min⁡(0,α∗(exp⁡(x)−1)))\text{SELU}(x) = \text{scale} * (\max(0,x) + \min(0, \alpha * (\exp(x) - 1))) SELU(x)=scale∗(max(0,x)+min(0,α∗(exp(x)−1)))

with α=1.6732632423543772848170429916717\alpha = 1.6732632423543772848170429916717α=1.6732632423543772848170429916717 and scale=1.0507009873554804934193349852946\text{scale} = 1.0507009873554804934193349852946scale=1.0507009873554804934193349852946 .

More details can be found in the paper Self-Normalizing Neural Networks .

Parameters

inplace (bool, optional) – can optionally do the operation in-place. Default: False

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.SELU()
>>> input = torch.randn(2)
>>> output = m(input)

CELU

class torch.nn.CELU(alpha=1.0, inplace=False)[source]

Applies the element-wise function:

CELU(x)=max⁡(0,x)+min⁡(0,α∗(exp⁡(x/α)−1))\text{CELU}(x) = \max(0,x) + \min(0, \alpha * (\exp(x/\alpha) - 1)) CELU(x)=max(0,x)+min(0,α∗(exp(x/α)−1))

More details can be found in the paper Continuously Differentiable Exponential Linear Units .

Parameters

alpha – the α\alphaα value for the CELU formulation. Default: 1.0
inplace – can optionally do the operation in-place. Default: False

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.CELU()
>>> input = torch.randn(2)
>>> output = m(input)

Sigmoid

class torch.nn.Sigmoid[source]

Applies the element-wise function:

Sigmoid(x)=11+exp⁡(−x)\text{Sigmoid}(x) = \frac{1}{1 + \exp(-x)} Sigmoid(x)=1+exp(−x)1

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.Sigmoid()
>>> input = torch.randn(2)
>>> output = m(input)

Softplus

class torch.nn.Softplus(beta=1, threshold=20)[source]

Applies the element-wise function:

Softplus(x)=1β∗log⁡(1+exp⁡(β∗x))\text{Softplus}(x) = \frac{1}{\beta} * \log(1 + \exp(\beta * x)) Softplus(x)=β1∗log(1+exp(β∗x))

SoftPlus is a smooth approximation to the ReLU function and can be used to constrain the output of a machine to always be positive.

For numerical stability the implementation reverts to the linear function for inputs above a certain value.

Parameters

beta – the β\betaβ value for the Softplus formulation. Default: 1
threshold – values above this revert to a linear function. Default: 20

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.Softplus()
>>> input = torch.randn(2)
>>> output = m(input)

Softshrink

class torch.nn.Softshrink(lambd=0.5)[source]

Applies the soft shrinkage function elementwise:

SoftShrinkage(x)={x−λ, if x>λx+λ, if x<−λ0, otherwise \text{SoftShrinkage}(x) = \begin{cases} x - \lambda, & \text{ if } x > \lambda \\ x + \lambda, & \text{ if } x < -\lambda \\ 0, & \text{ otherwise } \end{cases} SoftShrinkage(x)=⎩⎪⎨⎪⎧x−λ,x+λ,0, if x>λ if x<−λ otherwise

Parameters

lambd – the λ\lambdaλ value for the Softshrink formulation. Default: 0.5

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.Softshrink()
>>> input = torch.randn(2)
>>> output = m(input)

Softsign

class torch.nn.Softsign[source]

Applies the element-wise function:

SoftSign(x)=x1+∣x∣\text{SoftSign}(x) = \frac{x}{ 1 + |x|} SoftSign(x)=1+∣x∣x

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.Softsign()
>>> input = torch.randn(2)
>>> output = m(input)

Tanh

class torch.nn.Tanh[source]

Applies the element-wise function:

Tanh(x)=tanh⁡(x)=ex−e−xex+e−x\text{Tanh}(x) = \tanh(x) = \frac{e^x - e^{-x}} {e^x + e^{-x}} Tanh(x)=tanh(x)=ex+e−xex−e−x

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.Tanh()
>>> input = torch.randn(2)
>>> output = m(input)

Tanhshrink

class torch.nn.Tanhshrink[source]

Applies the element-wise function:

Tanhshrink(x)=x−Tanh(x)\text{Tanhshrink}(x) = x - \text{Tanh}(x) Tanhshrink(x)=x−Tanh(x)

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.Tanhshrink()
>>> input = torch.randn(2)
>>> output = m(input)

Threshold

class torch.nn.Threshold(threshold, value, inplace=False)[source]

Thresholds each element of the input Tensor.

Threshold is defined as:

y={x, if x>thresholdvalue, otherwise y = \begin{cases} x, &\text{ if } x > \text{threshold} \\ \text{value}, &\text{ otherwise } \end{cases} y={x,value, if x>threshold otherwise

Parameters

threshold – The value to threshold at
value – The value to replace with
inplace – can optionally do the operation in-place. Default: False

Shape:

Input: (N,∗)(N, *)(N,∗) where * means, any number of additional dimensions
Output: (N,∗)(N, *)(N,∗) , same shape as the input

Examples:

>>> m = nn.Threshold(0.1, 20)
>>> input = torch.randn(2)
>>> output = m(input)

Non-linear activations (other)

Softmin

class torch.nn.Softmin(dim=None)[source]

Applies the Softmin function to an n-dimensional input Tensor rescaling them so that the elements of the n-dimensional output Tensor lie in the range [0, 1] and sum to 1.

Softmin is defined as:

Softmin(xi)=exp⁡(−xi)∑jexp⁡(−xj)\text{Softmin}(x_{i}) = \frac{\exp(-x_i)}{\sum_j \exp(-x_j)} Softmin(xi)=∑jexp(−xj)exp(−xi)

Shape:

Parameters

dim (int) – A dimension along which Softmin will be computed (so every slice along dim will sum to 1).

Returns

a Tensor of the same dimension and shape as the input, with values in the range [0, 1]

Examples:

>>> m = nn.Softmin()
>>> input = torch.randn(2, 3)
>>> output = m(input)

Softmax

class torch.nn.Softmax(dim=None)[source]

Applies the Softmax function to an n-dimensional input Tensor rescaling them so that the elements of the n-dimensional output Tensor lie in the range [0,1] and sum to 1.

Softmax is defined as:

Softmax(xi)=exp⁡(xi)∑jexp⁡(xj)\text{Softmax}(x_{i}) = \frac{\exp(x_i)}{\sum_j \exp(x_j)} Softmax(xi)=∑jexp(xj)exp(xi)

Shape:

Returns

a Tensor of the same dimension and shape as the input with values in the range [0, 1]

Parameters

dim (int) – A dimension along which Softmax will be computed (so every slice along dim will sum to 1).

Note

This module doesn’t work directly with NLLLoss, which expects the Log to be computed between the Softmax and itself. Use LogSoftmax instead (it’s faster and has better numerical properties).

Examples:

>>> m = nn.Softmax(dim=1)
>>> input = torch.randn(2, 3)
>>> output = m(input)

Softmax2d

class torch.nn.Softmax2d[source]

Applies SoftMax over features to each spatial location.

When given an image of Channels x Height x Width, it will apply Softmax to each location (Channels,hi,wj)(Channels, h_i, w_j)(Channels,hi,wj)

Shape:

Returns

a Tensor of the same dimension and shape as the input with values in the range [0, 1]

Examples:

>>> m = nn.Softmax2d()
>>> # you softmax over the 2nd dimension
>>> input = torch.randn(2, 3, 12, 13)
>>> output = m(input)

LogSoftmax

class torch.nn.LogSoftmax(dim=None)[source]

Applies the log⁡(Softmax(x))\log(\text{Softmax}(x))log(Softmax(x)) function to an n-dimensional input Tensor. The LogSoftmax formulation can be simplified as:

LogSoftmax(xi)=log⁡(exp⁡(xi)∑jexp⁡(xj))\text{LogSoftmax}(x_{i}) = \log\left(\frac{\exp(x_i) }{ \sum_j \exp(x_j)} \right) LogSoftmax(xi)=log(∑jexp(xj)exp(xi))

Shape:

Parameters

dim (int) – A dimension along which LogSoftmax will be computed.

Returns

a Tensor of the same dimension and shape as the input with values in the range [-inf, 0)

Examples:

>>> m = nn.LogSoftmax()
>>> input = torch.randn(2, 3)
>>> output = m(input)

AdaptiveLogSoftmaxWithLoss

class torch.nn.AdaptiveLogSoftmaxWithLoss(in_features, n_classes, cutoffs, div_value=4.0, head_bias=False)[source]

Efficient softmax approximation as described in Efficient softmax approximation for GPUs by Edouard Grave, Armand Joulin, Moustapha Cissé, David Grangier, and Hervé Jégou.

Adaptive softmax is an approximate strategy for training models with large output spaces. It is most effective when the label distribution is highly imbalanced, for example in natural language modelling, where the word frequency distribution approximately follows the Zipf’s law.

Adaptive softmax partitions the labels into several clusters, according to their frequency. These clusters may contain different number of targets each. Additionally, clusters containing less frequent labels assign lower dimensional embeddings to those labels, which speeds up the computation. For each minibatch, only clusters for which at least one target is present are evaluated.

The idea is that the clusters which are accessed frequently (like the first one, containing most frequent labels), should also be cheap to compute – that is, contain a small number of assigned labels.

We highly recommend taking a look at the original paper for more details.

Warning

Labels passed as inputs to this module should be sorted accoridng to their frequency. This means that the most frequent label should be represented by the index 0, and the least frequent label should be represented by the index n_classes - 1.

Note

This module returns a NamedTuple with output and loss fields. See further documentation for details.

Note

To compute log-probabilities for all classes, the log_prob method can be used.

Parameters

Returns

Return type

NamedTuple with output and loss fields

Shape:

log_prob(input)[source]

Computes log probabilities for all n_classesn\_classesn_classes

Parameters

input (Tensor) – a minibatch of examples

Returns

log-probabilities of for each class ccc in range 0<=c<=n_classes0 <= c <= n\_classes0<=c<=n_classes , where n_classesn\_classesn_classes is a parameter passed to AdaptiveLogSoftmaxWithLoss constructor.

Shape:

predict(input)[source]

This is equivalent to self.log_pob(input).argmax(dim=1), but is more efficient in some cases.

Parameters

input (Tensor) – a minibatch of examples

Returns

a class with the highest probability for each example

Return type

output (Tensor)

Shape:

Normalization layers

BatchNorm1d

class torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)[source]

Applies Batch Normalization over a 2D or 3D input (a mini-batch of 1D inputs with optional additional channel dimension) as described in the paper Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift .

y=x−E[x]Var[x]+ϵ∗γ+βy = \frac{x - \mathrm{E}[x]}{\sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \betay=Var[x]+ϵ

x−E[x]∗γ+β

The mean and standard-deviation are calculated per-dimension over the mini-batches and γ\gammaγ and β\betaβ are learnable parameter vectors of size C (where C is the input size). By default, the elements of γ\gammaγ are set to 1 and the elements of β\betaβ are set to 0.

Also by default, during training this layer keeps running estimates of its computed mean and variance, which are then used for normalization during evaluation. The running estimates are kept with a default momentum of 0.1.

If track_running_stats is set to False, this layer then does not keep running estimates, and batch statistics are instead used during evaluation time as well.

Note

This momentum argument is different from one used in optimizer classes and the conventional notion of momentum. Mathematically, the update rule for running statistics here is x^new=(1−momentum)×x^+momentum×xt\hat{x}_\text{new} = (1 - \text{momentum}) \times \hat{x} + \text{momentum} \times x_tx^new=(1−momentum)×x^+momentum×xt , where x^\hat{x}x^ is the estimated statistic and xtx_txt is the new observed value.

Because the Batch Normalization is done over the C dimension, computing statistics on (N, L) slices, it’s common terminology to call this Temporal Batch Normalization.

Parameters

Shape:

Examples:

>>> # With Learnable Parameters
>>> m = nn.BatchNorm1d(100)
>>> # Without Learnable Parameters
>>> m = nn.BatchNorm1d(100, affine=False)
>>> input = torch.randn(20, 100)
>>> output = m(input)

BatchNorm2d

class torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)[source]

Applies Batch Normalization over a 4D input (a mini-batch of 2D inputs with additional channel dimension) as described in the paper Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift .

y=x−E[x]Var[x]+ϵ∗γ+βy = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \betay=Var[x]+ϵ

x−E[x]∗γ+β

If track_running_stats is set to False, this layer then does not keep running estimates, and batch statistics are instead used during evaluation time as well.

Note

Because the Batch Normalization is done over the C dimension, computing statistics on (N, H, W) slices, it’s common terminology to call this Spatial Batch Normalization.

Parameters

Shape:

Examples:

>>> # With Learnable Parameters
>>> m = nn.BatchNorm2d(100)
>>> # Without Learnable Parameters
>>> m = nn.BatchNorm2d(100, affine=False)
>>> input = torch.randn(20, 100, 35, 45)
>>> output = m(input)

BatchNorm3d

class torch.nn.BatchNorm3d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)[source]

Applies Batch Normalization over a 5D input (a mini-batch of 3D inputs with additional channel dimension) as described in the paper Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift .

y=x−E[x]Var[x]+ϵ∗γ+βy = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \betay=Var[x]+ϵ

x−E[x]∗γ+β

If track_running_stats is set to False, this layer then does not keep running estimates, and batch statistics are instead used during evaluation time as well.

Note

Because the Batch Normalization is done over the C dimension, computing statistics on (N, D, H, W) slices, it’s common terminology to call this Volumetric Batch Normalization or Spatio-temporal Batch Normalization.

Parameters

Shape:

Examples:

>>> # With Learnable Parameters
>>> m = nn.BatchNorm3d(100)
>>> # Without Learnable Parameters
>>> m = nn.BatchNorm3d(100, affine=False)
>>> input = torch.randn(20, 100, 35, 45, 10)
>>> output = m(input)

GroupNorm

class torch.nn.GroupNorm(num_groups, num_channels, eps=1e-05, affine=True)[source]

Applies Group Normalization over a mini-batch of inputs as described in the paper Group Normalization .

y=x−E[x]Var[x]+ϵ∗γ+βy = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta y=Var[x]+ϵ

x−E[x]∗γ+β

The input channels are separated into num_groups groups, each containing num_channels / num_groups channels. The mean and standard-deviation are calculated separately over the each group. γ\gammaγ and β\betaβ are learnable per-channel affine transform parameter vectors of size num_channels if affine is True.

This layer uses statistics computed from input data in both training and evaluation modes.

Parameters

Shape:

Examples:

>>> input = torch.randn(20, 6, 10, 10)
>>> # Separate 6 channels into 3 groups
>>> m = nn.GroupNorm(3, 6)
>>> # Separate 6 channels into 6 groups (equivalent with InstanceNorm)
>>> m = nn.GroupNorm(6, 6)
>>> # Put all 6 channels into a single group (equivalent with LayerNorm)
>>> m = nn.GroupNorm(1, 6)
>>> # Activating the module
>>> output = m(input)

SyncBatchNorm

class torch.nn.SyncBatchNorm(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True, process_group=None)[source]

Applies Batch Normalization over a N-Dimensional input (a mini-batch of [N-2]D inputs with additional channel dimension) as described in the paper Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift .

y=x−E[x]Var[x]+ϵ∗γ+βy = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \betay=Var[x]+ϵ

x−E[x]∗γ+β

The mean and standard-deviation are calculated per-dimension over all mini-batches of the same process groups. γ\gammaγ and β\betaβ are learnable parameter vectors of size C (where C is the input size). By default, the elements of γ\gammaγ are sampled from U(0,1)\mathcal{U}(0, 1)U(0,1) and the elements of β\betaβ are set to 0.

If track_running_stats is set to False, this layer then does not keep running estimates, and batch statistics are instead used during evaluation time as well.

Note

This momentum argument is different from one used in optimizer classes and the conventional notion of momentum. Mathematically, the update rule for running statistics here is x^new=(1−momentum)×x^+momemtum×xt\hat{x}_\text{new} = (1 - \text{momentum}) \times \hat{x} + \text{momemtum} \times x_tx^new=(1−momentum)×x^+momemtum×xt , where x^\hat{x}x^ is the estimated statistic and xtx_txt is the new observed value.

Because the Batch Normalization is done over the C dimension, computing statistics on (N, +) slices, it’s common terminology to call this Volumetric Batch Normalization or Spatio-temporal Batch Normalization.

Currently SyncBatchNorm only supports DistributedDataParallel with single GPU per process. Use torch.nn.SyncBatchNorm.convert_sync_batchnorm() to convert BatchNorm layer to SyncBatchNorm before wrapping Network with DDP.

Parameters

Shape:

Examples:

>>> # With Learnable Parameters
>>> m = nn.SyncBatchNorm(100)
>>> # creating process group (optional)
>>> # process_ids is a list of int identifying rank ids.
>>> process_group = torch.distributed.new_group(process_ids)
>>> # Without Learnable Parameters
>>> m = nn.BatchNorm3d(100, affine=False, process_group=process_group)
>>> input = torch.randn(20, 100, 35, 45, 10)
>>> output = m(input)

>>> # network is nn.BatchNorm layer
>>> sync_bn_network = nn.SyncBatchNorm.convert_sync_batchnorm(network, process_group)
>>> # only single gpu per process is currently supported
>>> ddp_sync_bn_network = torch.nn.parallel.DistributedDataParallel(
>>>                         sync_bn_network,
>>>                         device_ids=[args.local_rank],
>>>                         output_device=args.local_rank)

classmethod convert_sync_batchnorm(module, process_group=None)[source]

Helper function to convert torch.nn.BatchNormND layer in the model to torch.nn.SyncBatchNorm layer.

Parameters

default is the whole world

Returns

The original module with the converted torch.nn.SyncBatchNorm layer

Example:

>>> # Network with nn.BatchNorm layer
>>> module = torch.nn.Sequential(
>>>            torch.nn.Linear(20, 100),
>>>            torch.nn.BatchNorm1d(100)
>>>          ).cuda()
>>> # creating process group (optional)
>>> # process_ids is a list of int identifying rank ids.
>>> process_group = torch.distributed.new_group(process_ids)
>>> sync_bn_module = convert_sync_batchnorm(module, process_group)

InstanceNorm1d

class torch.nn.InstanceNorm1d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)[source]

Applies Instance Normalization over a 3D input (a mini-batch of 1D inputs with optional additional channel dimension) as described in the paper Instance Normalization: The Missing Ingredient for Fast Stylization .

y=x−E[x]Var[x]+ϵ∗γ+βy = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \betay=Var[x]+ϵ

x−E[x]∗γ+β

The mean and standard-deviation are calculated per-dimension separately for each object in a mini-batch. γ\gammaγ and β\betaβ are learnable parameter vectors of size C (where C is the input size) if affine is True.

By default, this layer uses instance statistics computed from input data in both training and evaluation modes.

If track_running_stats is set to True, during training this layer keeps running estimates of its computed mean and variance, which are then used for normalization during evaluation. The running estimates are kept with a default momentum of 0.1.

Note

This momentum argument is different from one used in optimizer classes and the conventional notion of momentum. Mathematically, the update rule for running statistics here is x^new=(1−momentum)×x^+momemtum×xt\hat{x}_\text{new} = (1 - \text{momentum}) \times \hat{x} + \text{momemtum} \times x_tx^new=(1−momentum)×x^+momemtum×xt , where x^\hat{x}x^ is the estimated statistic and xtx_txt is the new observed value.

Note

InstanceNorm1d and LayerNorm are very similar, but have some subtle differences. InstanceNorm1d is applied on each channel of channeled data like multidimensional time series, but LayerNorm is usually applied on entire sample and often in NLP tasks. Additionaly, LayerNorm applies elementwise affine transform, while InstanceNorm1d usually don’t apply affine transform.

Parameters

Shape:

Examples:

>>> # Without Learnable Parameters
>>> m = nn.InstanceNorm1d(100)
>>> # With Learnable Parameters
>>> m = nn.InstanceNorm1d(100, affine=True)
>>> input = torch.randn(20, 100, 40)
>>> output = m(input)

InstanceNorm2d

class torch.nn.InstanceNorm2d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)[source]

Applies Instance Normalization over a 4D input (a mini-batch of 2D inputs with additional channel dimension) as described in the paper Instance Normalization: The Missing Ingredient for Fast Stylization .

y=x−E[x]Var[x]+ϵ∗γ+βy = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \betay=Var[x]+ϵ

x−E[x]∗γ+β

By default, this layer uses instance statistics computed from input data in both training and evaluation modes.

Note

This momentum argument is different from one used in optimizer classes and the conventional notion of momentum. Mathematically, the update rule for running statistics here is x^new=(1−momentum)×x^+momemtum×xt\hat{x}_\text{new} = (1 - \text{momentum}) \times \hat{x} + \text{momemtum} \times x_tx^new=(1−momentum)×x^+momemtum×xt , where x^\hat{x}x^ is the estimated statistic and xtx_txt is the new observed value.

Note

InstanceNorm2d and LayerNorm are very similar, but have some subtle differences. InstanceNorm2d is applied on each channel of channeled data like RGB images, but LayerNorm is usually applied on entire sample and often in NLP tasks. Additionaly, LayerNorm applies elementwise affine transform, while InstanceNorm2d usually don’t apply affine transform.

Parameters

Shape:

Examples:

>>> # Without Learnable Parameters
>>> m = nn.InstanceNorm2d(100)
>>> # With Learnable Parameters
>>> m = nn.InstanceNorm2d(100, affine=True)
>>> input = torch.randn(20, 100, 35, 45)
>>> output = m(input)

InstanceNorm3d

class torch.nn.InstanceNorm3d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)[source]

Applies Instance Normalization over a 5D input (a mini-batch of 3D inputs with additional channel dimension) as described in the paper Instance Normalization: The Missing Ingredient for Fast Stylization .

y=x−E[x]Var[x]+ϵ∗γ+βy = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \betay=Var[x]+ϵ

x−E[x]∗γ+β

By default, this layer uses instance statistics computed from input data in both training and evaluation modes.

Note

This momentum argument is different from one used in optimizer classes and the conventional notion of momentum. Mathematically, the update rule for running statistics here is x^new=(1−momentum)×x^+momemtum×xt\hat{x}_\text{new} = (1 - \text{momentum}) \times \hat{x} + \text{momemtum} \times x_tx^new=(1−momentum)×x^+momemtum×xt , where x^\hat{x}x^ is the estimated statistic and xtx_txt is the new observed value.

Note

InstanceNorm3d and LayerNorm are very similar, but have some subtle differences. InstanceNorm3d is applied on each channel of channeled data like 3D models with RGB color, but LayerNorm is usually applied on entire sample and often in NLP tasks. Additionaly, LayerNorm applies elementwise affine transform, while InstanceNorm3d usually don’t apply affine transform.

Parameters

Shape:

Examples:

>>> # Without Learnable Parameters
>>> m = nn.InstanceNorm3d(100)
>>> # With Learnable Parameters
>>> m = nn.InstanceNorm3d(100, affine=True)
>>> input = torch.randn(20, 100, 35, 45, 10)
>>> output = m(input)

LayerNorm

class torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True)[source]

Applies Layer Normalization over a mini-batch of inputs as described in the paper Layer Normalization .

y=x−E[x]Var[x]+ϵ∗γ+βy = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta y=Var[x]+ϵ

x−E[x]∗γ+β

The mean and standard-deviation are calculated separately over the last certain number dimensions which have to be of the shape specified by normalized_shape. γ\gammaγ and β\betaβ are learnable affine transform parameters of normalized_shape if elementwise_affine is True.

Note

Unlike Batch Normalization and Instance Normalization, which applies scalar scale and bias for each entire channel/plane with the affine option, Layer Normalization applies per-element scale and bias with elementwise_affine.

This layer uses statistics computed from input data in both training and evaluation modes.

Parameters

Shape:

Examples:

>>> input = torch.randn(20, 5, 10, 10)
>>> # With Learnable Parameters
>>> m = nn.LayerNorm(input.size()[1:])
>>> # Without Learnable Parameters
>>> m = nn.LayerNorm(input.size()[1:], elementwise_affine=False)
>>> # Normalize over last two dimensions
>>> m = nn.LayerNorm([10, 10])
>>> # Normalize over last dimension of size 10
>>> m = nn.LayerNorm(10)
>>> # Activating the module
>>> output = m(input)

LocalResponseNorm

class torch.nn.LocalResponseNorm(size, alpha=0.0001, beta=0.75, k=1.0)[source]

Applies local response normalization over an input signal composed of several input planes, where channels occupy the second dimension. Applies normalization across channels.

bc=ac(k+αn∑c′=max⁡(0,c−n/2)min⁡(N−1,c+n/2)ac′2)−βb_{c} = a_{c}\left(k + \frac{\alpha}{n} \sum_{c'=\max(0, c-n/2)}^{\min(N-1,c+n/2)}a_{c'}^2\right)^{-\beta} bc=ac⎝⎛k+nαc′=max(0,c−n/2)∑min(N−1,c+n/2)ac′2⎠⎞−β

Parameters

Shape:

Examples: