OpenCV Eigen Sophus PCL G2O

外用库学习笔记

- OpenCV
- - 需知
  - OpenCV的结构
  - OpenCV modules
  - 头文件
  - 数据类型
  - 示例
  - - 显示图片
    - 视频
    - 从摄像头中读取
    - 读取文件并存放
    - 读取配置文件
    - 保存图片到文件
    - 图像的像素
    - 绘图
    - 随机选择颜色
    - 取整函数
    - 关键点和描述子
    - 对极几何
    - 计算极线
    - 单应函数
    - 透视变换
    - 填充多边形
    - step
    - fastAtan2
- Eigen
- - 头文件
  - 示例
  - Eigen中旋转的相互转化
  - 注意
- Sophus
- - 需知
  - 示例
- Pangolin
- - 需知
- PCL - Point Cloud Library
- - 需知
  - 说明
  - 数据类型
  - 示例
  - - 点云的创建
    - 点云的转换
    - 下采样
    - 离群点的去除
    - 离群点的显示
    - 移动最小二乘
    - 法线的估计
    - 贪心投影三角化
    - 输出点云文件
- 图优化 g2o
- - g2o的基本框架结构
  - 示例
  - - 求解器
    - 设置顶点
    - 设置边

OpenCV

https://docs.opencv.org/3.1.0/

需知

查看OpenCV安装版本pkg-config --modversion opencv

当系统已安装过opencv，再次安装不同版本的opencv时，需要修改安装路径，防止覆盖之前的版本。
安装路径的修改在cmake -DCMAKE_INSTALL_PREFIX=/.....，不同于默认修改路径/usr/local。或者sudo make install DESTDIR=/....中修改。
切换OpenCV不同版本:在~/.bashrc中加入

export PKG_CONFIG_PATH={opencv安装路径/.../lib/pkgconfig}
export LD_LIBRARY_PATH={opencv安装路径/.../lib}

source ~/.bashrc
也可以通过修改CMakeLists文件

set(OpenCV_DIR "...../build")
find_package(OpenCV REQUIRED)

OpenCV的结构

是层级结构组织：最上层是 OpenCV 和操作系统的交互，接下来是语言绑定和示例应用程序，再下一层是 opencv_contrib模块所包含的 OpenCV 由其他开发人员所贡献的代码。，包含大多数高层级的函数。

OpenCV modules

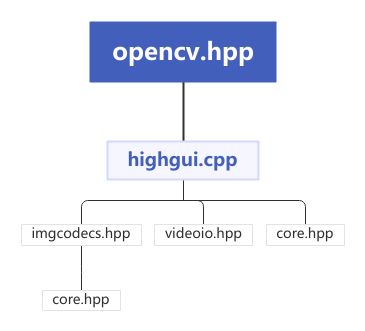
core 包含 OpenCV 库的基础结构以及基本操作
improc 图像处理模块包含基本的图像转换，包括滤波以及类似的卷积操作
imcodecs videoio highgui 包含可以用来显示图像或者简单的输入的用户交互函数。可以看作是一个非常轻量级的 Windows UI 工具包
video 包含读取和写视频流的函数
calib3d 校准单个、双目记忆多个相机的算法实现
多个cude*模块主要是函数在 CUDA GPU 上的优化实现，此外，还有一些仅用于 GPU 的功能。其中一些函数能狗返回很好的结果，但需要足够好的计算资源，如果硬件没有 GPU，则不会有什么提升。

头文件

CMakelists

find_package (OpenCV 3 REQURIED)
include_directories(${OpenCV_INCLUDE_DIR})
...
target_link_libraries(${PROJECT_NAME} ${OpenCV_LIBS})

opencv2/opencv.hpp由于包含了各个模块的头文件，如opencv2/core.hpp等。因此，可以使用opencv2/opencv.hpp来包含说有可能在 OpenCV 函数中用到的头文件，但会减慢编译速度。

通过指令locate opencv | less ，/ modules可找到头文件所在的 .../modules 文件夹，其对应的源文件都在modules/xxxx/src/中

数据类型

从组织结构来看：

直接从C++言语中继承的基础数据类型：int float等。这些类型包括简单的数组和矩阵，也代表一些简单的几何概念，比如点、矩阵、大小等
辅助对象。垃圾收集指针类、用于数据切片的范围对象以及抽象的终止条件类等。
大型数组类型。cv::Mat cv::SparseMat。
还是用了很多标准模板库STL，尤其依赖vector类。

基础类型概述
固定向量类：
模板类cv::Vec< >，即使cv::Vec< >是模板，但是通常不会使用这个形式，而是使用别名typedef，如cv::Vec2i cv::Vec3i等。用于已知维度的小型变量。在编译前必须已知维度。

cv::Vec{2,3,4,6}{b,w,s,i,f,d}；//相互组合
b = unsigned char; w  = unsigned short; s = short;
i = int;  f = float; d = double;

固定矩阵类
与模板类cv::Mat< >相关联。适用于特定的小型矩阵操作，在编译前必须已知维度。区别于cv::Mat

cv::Matx{1,2,3,4,6}{1,2,3,4,6}{f,d}

cv::Mat K = ( cv::Mat_<double> ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );

cv::Point类
Point类不是从固定向量类继承下来的，而是由自己的模板派生的，但是同时它们可以从固定向量类转换得到。Point类与固定向量类之间最大的不同是它们的成员函数是通过名称变量访问的mypoint.x，而不是通过访问下标myvec[0]。和cv::Vec< >一样，是通过别名调用作为一个正确模板的实例。这些别名可以是cv::Point2i cv::Point2f 等。

操作	示例
默认构造函数	`cv::Point2i p` `cv::Point3i`
复制构造函数	`cv::Point3d p2(p1)`
值构造函数	`cv::Point2i (x0,x1)` `cv::Point3d p(x0,x1,x2)`
构造固定向量类	`(cv::Vec3f) p;`
成员访问	`p.x,p.y`
点乘	`float x = p1.dot(p2)`
叉乘	`double x = p1.cross(p2)`

cv::Scalar类
本质上是一个思维Point类。cv::Scalar一般是双精度四元素向量的别名，是通过整数下标来访问的，这与cv::Vec< >相同。是因为cv::Scalar直接继承cv::Vec。

操作	示例
默认构造函数	`cv::Scalar s`
复制构造函数	`cv::Scalar s2(s1)`
值构造函数	`cv::Scalar s(x0)` `cv::Scalar s(x0,x1,x2,x3)`
元素相乘	`s1.mul(s2)`
四元数共轭	`s.conj();//return cv::Scalar(s0, -s1, -s2,-s3);`
四元数真值测试	`s.isReal();//return true, if s1==s2==s3==0;`

const Scalar& color;
Scalar color = Scalar(* ,* ,*);//* 表示0-255
Scalar color = Scalar(255);//表示B=255，GR为0

颜色都是下限0指的是黑色，上限255或者1指的是白色。光的成色原理是加法，也就是从黑色到白色，从0到1，在黑暗的情况下，加上三原色变亮。颜料的成色原理是减法，也就是从白色到黑色，从1到0，白纸上使用颜料变暗。
(0,0,0)为RGB。RGB为加法。BGR顺序。

Size类
在实际操作中与Point相似，且可以与Point相互转换。主要区别是成员函数的不同。
Size类的三个别名为cv::Size cv::Size2i cv::Size2f。前两个为等价的，表示整数大小，而最后一个是表示32位浮点大小

操作	示例
默认构造函数	`cv::Size sz;` `cv::Size2i sz;` `cv::Size2f sz;`
复制构造函数	`cv::Size sz2(sz1)`
值构造函数	`cv::Size2f sz(w, h)`
成员访问	`sz.width(); sz.height()`
计算面积	`sz.area();`

辅助对象
cv::Ptr模板
首先，需要为想要封装的对象定义一个指针模板的实例。可以通过调用类似cv::Ptr p(new cv::Matx33f)或cv::Ptr p = makePtr ()的形式实现。

示例

#include "opencv2/"下的

头文件	函数
`imagcodecs.hpp`	`imread` `imwrite`
`highgui.hpp`	`namedWindow` `imshow` `waitkey` `destoryWindow`
`videoio.hpp`	`VideoCapture`
`utility.hpp`	`glob`
`features2d/features2d.hpp`	`FeatureDetector`
`calib3d/calib3d.hpp`	`findFundamentalMat()` `computeCorrespondEpilines()`

显示图片

    cv::Mat img = cv::imread(argv[1], -1);
    if (img.empty())
        return -1;
    cv::namedWindow("Example1", cv::WINDOW_AUTOSIZE);
    cv::imshow("Example1", img);
    cv::waitKey(0);
    cv::destroyWindow("Example1");
    return 0;

imread 从磁盘读取各种图像，返回一个 Mat 结构。 Loads an image from a file.

cv::Mat cv::imread( 
	const String& filename,                   //Input filename
	int    flags = cv::IMREAD_COLOR //Flags set how to interpret file
);

FLAGS可以设置为以下任意一个值

标志	含义	默认值
`cv::IMREAD_COLOR`	总是读取三通道图像	是
`cv::IMREAD_GRAYSCALE`	总是读取单通道图像	否
`cv::IMREAD_ANYCOLOR`	通道数由文件实际通道数决定（不超过3）	否
`cv::IMREAD_ANYDEPTH`	允许加载超过8bit深度	否
`cv::IMREAD_UNCHANGED`	等于将`cv::IMREAD_ANYCOLOR`和`cv::IMREAD_ANYDEPTH`组合了起来，但也不完全是	否

imwrite保存图像 Save an image to a specified file.

bool cv::imwrite(
	const String& filename,    //Input filename
	cv::InputArray image,      //Image to write to file
	const vector<int>& params = vector<int>()  //(Optional) for parameterized fmts
);

第一个参数给定了文件名，文件名的拓展名部分用来决定以何种格式保存图像，以下是对应的扩展名

拓展名	保存格式	通道
`.jpg/.jpeg`	以`baseline JPEG`格式保存	8位数据，单通道或三通道输入
`*.jp2`	`JPEG2000`	8位或16位数据，单通道或三通道输入
`.tif/.tiff`	`TIFF`	8位或16位数据，单通道、三通道或四通道输入
`*.png`	`PNG`	8位或16位数据，单通道、三通道或四通道输入
`*.bmp`	`BMP`	单通道、三通道或四通道输入
`.ppm/.pgm`	`NetPBM`	8位数据，单通道(PGM)或三通道(PPM)

第二个参数是待存储的输入图像。
第三个参数是被作用特殊类型文件的写入操作时所需的数据。
cv::imwrite是为图像文件定制的。

namedWindow 赋一个名字给窗口，未来 Highgui 和这个窗口交互通过赋予的名字。第二个参数书名了 Window 的特性，可以全部设置为0（默认情况），也可以设置为cv::WINDOW_AUTOSIZE。

imshow 将创建一个窗口，如果窗口不存在，它会自动调用cv::namedWindow()建立一个窗口。无论何时，只要在cv::Mat中拥有一个图像结构，都可以通过cv::imshow()显示。This function should be followed by cv::waitKey function which displays the image for specified milliseconds. Otherwise, it won’t display the image.

waitkey cv::waitKey(0);函数告诉系统暂停并等待键盘事件。如果传入一个大于零的参数，它将会等待等同于该参数的毫秒时间，然后执行程序；如果参数被设置为0 或者一个负数，程序将会一直等到有键被按下。

因为有cv::Mat，图像将会在生命周期结束自动释放，其行为类似 STL 中的容器类。这种自动内存释放由内部的引用指针所控制。

destoryWindow将会关闭窗口并释放掉相关联的内存空间。

在更长、更复杂的代码中，程序员应该在窗口的生命周期自然结束之前自主销毁窗口以防内存泄露。

视频

OpenCV 播放视频与图像的唯一区别就是需要用循环读取视频序列中的每一帧，还需要来跳出循环。

    cv::namedWindow("Example3", cv::WINDOW_AUTOSIZE);
    cv::VideoCapture cap;
    cap.open( string(argv[1]));//读取视频
    cv::Mat frame;//声明了一个可以保存视频帧的结构
    for (;;){
        cap >> frame;
        if (frame.empty()) break;
        cv::imshow("Example3", frame);
        if (cv::waitKey(33) >= 0) break;
    }

string(argv[1])是string的构造函数。

VideoCapture可以打开和关闭许多类型的ffmpeg支持的视频文件。
cv::watikey(33) 表示每一帧图片显示后都会等待 33 毫秒。为什么是33毫秒，是因为这能让视频以30FPS的速率播放，并且能够允许用户在播放的时候打断。根据以往的经验，最好去检查VideoCapture结构来确定视频真正的帧率。

从摄像头中读取

    cv::VideoCapture cap;
    if(argc == 1){
        cap.open(0);//open the first camera
    } else  {
        cap.open(argv[1]);
    }
    if ( !cap.isOpened()){//check if we succeeded
        std::cerr << "Couldn't open capture." << std::endl;
        return -1;
    }

通过cv::VideoCapture对硬盘上的文件和摄像头是有一致的接口的。对于前者来说，需要给它一个指示读取文件名的路径；对于后者来说，需要给它一个相机的 ID 号，（如果只有一个摄像头链接，这个 ID 号通常为0）。ID 的默认值是-1，这意味着随意选择一个。

读取文件并存放

utility.hpp
void cv::glob( String pattern, std::vector & result, bool recursive = false);

读取路径pattern中的文件，并存入result中

cv::String filepath = " ...";
std::vector<cv::String> result;
cv::glob ( filepath, result);

读取配置文件

XML/YAML file storage class that encapsulates all the information necessary for writing or reading data to/from a file.

cv::FileStorage::FileStorage	(	const String & 	source,
									int 	flags,
									const String & 	encoding = String() 
)

Parameter
source Name of the file to open or the text string to read the data from. Extension of the file (.xml or .yml/.yaml) determines its format (XML or YAML respectively). Also you can append .gz to work with compressed files, for example myHugeMatrix.xml.gz. If both FileStorage::WRITE and FileStorage::MEMORY flags are specified, source is used just to specify the output file format (e.g. mydata.xml, .yml etc.).
flags Mode of operation. See FileStorage::Mode
encoding Encoding of the file. Note that UTF-16 XML encoding is not supported currently and you should use 8-bit encoding instead of it.

保存图片到文件

bool cv::imwrite(const String & filename, InputArray img, const std::vector ¶ms = std::vector() );

图像的像素

最简单的图像——灰度图。在一张灰度图中，每个像素位置 $(x, y)$ 对应一个灰度值 $I$ ，所以一张宽度为 $w$ 、高度为 $h$ 的图像，数学上可以记为一个函数： $I(x,y):\mathbb{R}^2\to \mathbb{R}$
其中， $(x, y)$ 是像素的坐标。像素是位置坐标，每个像素中的存储值为与图片相关的值。
如灰度图存储的为灰度值，灰度值一般用0-255的整数表示，255为纯白色。一张宽度为640像素、高度为480像素分辨率的灰度图可以表示为 uchar image[480][640]。分辨率中的宽度代表列数col，高度代表行数row。

uchar pixel = image[y][x]
uchar pixel = image.at<uchar>(y,x)
uchar pixel = *image.ptr<uchar>(y.x);

读取[x][y]的像素。一个像素的灰度可以用8位整数记录，也就是一个 $0\sim 2^8-1$
在RGB-D相机的深度图中，记录了各个像素与相机之间的距离，这个距离通常以毫米为单位，而RGB-D相机的量程在十几米左右，超过了255。通常会采用16位整数，unsigned short来记录深度图的信息， $0\sim 2^{16}-1$ 。彩色图像的表示则需要通道（channel）的概念。在计算机中，使用红绿蓝三色来组合任意色彩。对于每一个像素，都要记录其R、G、B三个数值，每个数值就成为一个通道。如最常见的彩色图像有三个通道，每个通道都由8位整数表示。在这种规定下，一个像素占24位空间。也就是得到一个24位的像素，每8位代表一个颜色的色值，如果还想表达图像的透明度，就使用RGBA。在OpenCV中默认顺序为BGR。

用指针遍历像素，速度优于逐个遍历像素

for ( size_t y = 0; y < image.rows; y++ ) {
	uchar *row_ptr = image.ptr<uchar>(y);// 图像的行指针 row_ptr是第
										 // 行的头指针
	for ( size_t x = 0; x < image.cols; x++) {
		uchar *data_ptr = &row_ptr[x * image.channels()];//data_ptr 指向待访问的像素数据
	}
}

遍历像素：
外层循环是for (int n; n < rows; n++)，内层循环是for (int n; n < rcols; n++)。因为是先行循环，后列循环。注意对应rows 和 cols。
循环内的程序，注意n和m对应的与图片像素的关系。[m][n]是与图片有关，但是行列元素还是正常表示。

绘图

cv::circle()

void circle(
	cv::Mat&   img, //Image to be drawn on
	cv::Point  center,//Location of circle center
	int  radius, //Radius of circle
	const cv::Scalar& color, //Color, RGB form
	int  thickness = 1,//Thickness of line]
	int  linetype = 8,//Connectedness, 4 or 8
	int  shift = 0//Bits of radius to treat as fraction
);

第二个参数是圆心的二维坐标点，然后是radius color thickness 等应用在圆心和半径上。

cv::line()

void line (
	cv::Mat&  img, //Image to be drawn on
	cv::Point  pt1,//First endpoint of line
	cv::Point  pt2,//Secoind endpoint of line
	const cv::Scalar& color,//Color，BGR form
	int  linetype = 8,//Connectedness, 4 or 8
	int  shift = 0 //Bits of radius to treat as fraction
);

在图像img上绘制一条从pt1到pt2的直线。直线自动被图像边缘截断。

随机选择颜色

RNG rng;
Scalar color = Scalar( rng(255), rng(255), rng(255));

随机数发生器 cv::RNG
一个随机数对象RNG用来产生随机数的伪随机序列。这样做的好处是你可以方便的得到多重伪随机数流。在写大型系统时，在不同的代码模块中使用不同的随机数流是个好习惯。这样的话，当你移除一个模块时，不会改变其他模块中的随机数流。

cv::RNG()

cv::RNG::RNG ( void );
cv::RNG::RNG ( uint64 state);  //create using the seed 'state'

可以使用默认构造函数来创建一个RNG对象，或者传递一个64位的无符号整形数，这个数将用来作为随机数序列的种子。如果调用默认的构造函数（或者第二个参数为0），这个生成器将使用一个定制来初始化。

cv::theRNG()

cv::RNG& theRNG (void); //return a random number generator

该函数为了调用它的线程返回一个默认的随机数生成器。OpenCV自动为每一个执行中的线程创建一个cv::RNG的实例。如果你只想要一个数或者只初始化一个数组，这些函数就很方便。然后，如果你有一个循环需要产生大量随机数，最好使用一个随机数生成器。通过使用RNG::operator T()来得到自己的随机数。

cv::RNG::operator T()
T是数据类型

cv::RNG::operator uchar();
cv::RNG::operator schar();
cv::RNG::operator ushort();
cv::RNG::operator short int();
cv::RNG::operator int();
cv::RNG::operator unsigned();
cv::RNG::operator float();
cv::RNG::operator double();

上述都是强制类型转化，重载的类型转换操作符()

cv::RNG rng = cv::theRNG();
cout << "An integer: " << (int)rng << endl;
cout << "Another integer: " << int(rng) << endl;
cout << "A float: " << (float)rng << endl;
cout << "Another float: " << float(rng) << endl;

产生整数的死后，将覆盖整个取值范围；当产生浮点数时，它们的范围始终是 $[0.0, 1.0)$ 。

取整函数

函数cvRound(),cvFloor(),cvCeil()

cvRound():返回跟参数最接近的整数值，即四舍五入
cvFloor():返回不大于参数的最大整数值，即向下取整
cvCeil():返回不小于参数的最小整数值，即向上取整

关键点和描述子

关键点和描述子的分析

搜索图像中所有关键点
为每个关键点创造描述子
将描述子和先有的描述集比较，查找匹配项

cv::KeyPoint对象

class cv::KeyPoint {
public:
	cv::Point2f pt; //coodinates of the keypoint
	float size://diameter of the meaningful keypoint neighborhood
	float angle;//computed orientation of the keypoints (-1 if none)
	float response;/response for which the keypoints was selected
	...
}

每个关键点都有一个cv::Point2f成员，这告诉我们它位于哪里。size是关于关键点周围区域的某些信息，或者在某种程度上包含关键点存在于第一位的判定，或者将在该关键点的描述子中发挥的作用。关键点的angle只对某些关键点有意义。response用于能够对一个关键点比另一个关键点更强做出响应的检测器。
cv::KeyPoint对象有两个构造函数，基本相同，区别在于使用两个浮点数还是单个cv::Point2f对象来设置关键点的位置。

为了找到关键点且/或计算描述子，有cv::Feature2D类，有一些叫做cv::FeatureDetector和cv::DescriptorExtractor的类，适用于单纯的特征检测或描述子提取算法的单独的类。在OpenCV 3.x开始，是通过typedef定义的cv::Feature2D的同义词，typedef Feature2D FeatureDetector等

using namespace cv;
Ptr<FeatureDetector> detector;
Ptr<DescriptorExtractor> descriptor;

如果是单纯的关键点检测算法，如FAST，实际的实现可能只是执行cv::Feature2D::detect()；如果它是一个纯特征描述算法，如FREAK，实际的实现可能只是cv::Feature2D::compute()；在要求完全解决的算法的情况下，如SIFT、SURF、ORB等，实际的实现就会是cv::Feature2D::detectAndCompute()，在这种情况下，detect()和compute()会被隐式调用

detect(image, keypoints, mask) ~ detectAndCompute(image, mask, keypoints, noArray(), false)
cv::Feature2D::detect()方法直接或通过调用detectAndCompute()进行关键点的基本工作。第一个方法需要输入图像、关键点向量和可选掩码（掩码就是屏蔽图片，位图掩码，就是将图片的每个像素和掩码中对应的像素进行与运算， 1&23=23 ，0&89= 0）。然后搜索图像中的关键点，并找到的任何内容放置在你提供的向量中。第二个方法完全做相同的事情，不同的是它合计一个图像的向量、一个掩码的向量（或者根本没有）以及关键点向量的向量

vector<KeyPoint> kp1, kp2;
detector->detect(rgb1, kp1);
detector->detect(rbg2, kp2);

一旦找到关键点，接下来就是计算描述子。

compute(image, keypoints, descriptors) ~ detectAndCompute(image, noArray(), keypoints, descriptors, true)
第一个compute()方法需要一个图像、一个关键点列表、cv::Mat格式的输出 — 被compute()用于放置计算出的特征。
由cv::Feature2D派生的对象生成的所有描述子都可以表示为固定长度的向量，因此可以将他们全部排列成序列。一个使用的惯例是每行描述子都是单独的描述子，并且这些行的数量等于关键点中的元素的数量。
要一次处理几个图像时，将使用第二种compute()，在此情况下，图像的参数需要一个其中包含你想要处理的所有图像的STL向量。关键点参数需要一个包含关键点向量的向量，描述子参数需要一个包含可用于存储所有生成的描述子的数组的向量。这种方法通常和对图像detect()同时出现，并需要向给detect()方法那样输入的图像和从那种方法接受到的关键点。

Mat desp1, desp2;
descriptor->compute(rgb1, kp1, desp1);
descriptor->compute(rgb2, kp2, desp2);

cv::DMatch对象
一般来说，匹配器将是一个尝试将一个图像中的关键点与其他单个图像或称为字典的其他图像的几何进行匹配的对象。

class cv::DMatch {
public:
	DMatch();//set this->distance 
	DMatch( int _queryIdx, int _trainIdx, float _distance );
	DMatch( int _queryIdx, int _trainIdx, int _imgIdx, float _distance );	
	int queryIdx; // query descriptor index
	int trainIdx; // train descriptor index
	int imgIdx; // train image index
	float distance;
	
	bool operator<( const DMatch &m ) const; //Comparsion operator
											// based on 'distance'
}

cv::DMatch的数据成员是queryIdx,trainIdx,imgIdx和distance。前两个辨别与每个图像中的关键点列表匹配的关键点。OpenCV库使用的惯例是将这两幅图像分别作为搜索图像（“新”图像）和训练图像（“旧”图像）。imgIdx是用来辨别在图像和字典之间需求匹配的情况下训练图像来自的特定图像。distance是用来表示匹配的质量的，通常来讲，是它们存在的多维向量空间中的两个关键点之间的欧氏距离，虽然不总是衡量标准，但是如果两个不同的匹配具有不同的距离值，则距离值越小，匹配越好。为了促进这种比较，定义了运算符cv::DMatch::operator<()，这允许两个cv::DMatch对象直接在它们的距离成员的含义上进行比较。

cvDescriptorMatcher类接口提供了三个函数match(),knnMatch(),radiusMatch()，对于每个函数都用两种形式，一个是用于识别（需要一个特征列表以及经过训练的字典），另一个是用于跟踪（需要两个特征列表）。match()通常需要cv::Mat格式的单个关键字描述子列表queryDescriptors。在这种情况下，请记住每个行代表单个描述子，每列是该描述符向量表示的一个维度。match()还需要一个cv::DMatch对象的STL向量，它可以填充各个检测到的匹配项。在match()方法的情况下，查询列表上的每个关键点将与列表中的“最佳匹配”匹配。
match()也支持可选的mask参数。与OpenCV中的大多数mask参数不同，该掩码不再像素空间中操作，而是在描述子的空间中。mask参数是cv::Mat对象的STL向量。该向量中的每个矩阵对应于字典中的训练图像之一（字典中的一个对象）。

vector<DMatch> matches;
BFMatcher matcher;
matcher.match(desp1, desp2, matches);
cout << "Find total " << matches.size() << " matches." << endl;

对极几何

#include 
cv:: Mat cv::findFundamentalMat(     //compute fundamental mtx
	cv::InputArray  points1,		 //Points image 1 (float)
	cv::InputArray points2,	     	 //Points image 2 (float)
	int    method = cv::FM_RANSAC,	 //Method for computing mtx
	double  param1 = 3.0,		     //RANSAC max distance
	double param2 = 0.99,		     //RANSAC/lmedS confidence
	cv::OutputArray  mask = cv::noArray() //(Optional) array
										  //indicates used elements
);

前两个参数是二维或者三维点的数组，以任何常规方式排列。对于三维点 $(x, y, z)$ 来说，最终将被缩放为 $(x / z, y / z)$ ，或者可以在单应性坐标系中输入二维点 $(x, y, 1)$ ，用相同的做法处理。
第三个参数决定了通过对应点计算基本矩阵的方法，边切可以采用四个值之中的一个。对于每个值，对于point1和point2中所需点的数量有特定的约束，如下表

方法的值	点数	算法
`cv::FM_7POINT`	$N = 7$	7点算法
`cv::FM_8POINT`	$N\geq 8$	8点算法
`cv::FM_RANSAC`	$N\geq 8$	RANSAC算法
`cv::FM_LMEDS`	$N\geq 8$	LMedS算法
7点算法遵循矩阵 $F$ 的秩必须为2，来完全约束矩阵。
8点算法通过线性方程组求解。
超过8个点，则要求所有点的线性最小二乘解。
上述算法对异常值十分敏感，这个问题由RANSAC和LMedS解决，具有消除异常值和辨识的能力。param1是从点到极线（像素）的最大距离，超过此距离被认为是异常值。param2是期望置信度（0~1之间），实际上告诉算法的迭代次数。
函数返回通常是一个与点精度相同的3X3的矩阵。经过计算的基本矩阵之后通常被传递到函数`cv::computeCorrespondEpilines()`，以找到对应指定点的极线，或者传递到`cv::stereoRectifyUncalibrated()`，以计算得到标定变换。

计算极线

#include
cv::computeCorrespondEpilines()根据一幅图像中的点列，计算其在另一幅图像中对应的极线。每条计算的极线以三点 $(a, b, c)$ 的形式编码，极线的定义如下
$a\cdot x+b\cdot y+c=0$
为了计算这些极线，函数需要利用通过函数cv::findFundamentalMat()得到的基本矩阵

void cv::computeCorrespondEpilines(
	cv::InputArray points,   //Input points, Nx1  or 1xN (Nc=2) or vector
	int  whichImage,         //Index of image which contains points ('1' or '2')
	cv::InputArray F,        //Fundamental matrix
	cv::OutputArray lines,   //Output vector of lines, encoded as tuples (a,b,c)							
);

第一个参数points为二维或者三维点的输入数组。参数whichImage必须是1或者2，并标明哪幅图的点被定义，与函数中的数组points1和points2相关联。F是由函数cv::findFundamentalMat()返回的3X3矩阵。最后，lines是浮点数型数组(Vec3f Vec3d会出现报错），表示将写入的结果极线。每一条极线都以一个三元素向量 $L = (a, b, c)$ 的形式编码，包含极线等式 $a\cdot x+b\cdot y+c=0$ 的参数。由于极线等式与参数a,b,c的所有归一化无关，它们被默认归一化，使得 $a^2+b^2=1$ .

单应函数

cv::findHomography()，它将一系列对应点作为输入，返回最能描述这些对应点的单应性矩阵。至少需要四点来求解H。

cv::Mat cv::findHomography(
	cv::InputArray  srcPoints, // Input array source points (2-d)
	cv::InputArray  dstPoints, // Input array result points (2-d)
	cv::int  method  =  0 , //0, cv::RANSAC, cv::LMEDS, etc.
	double  ransacReprojThreshold = 3, //Max reprojection error
	cv::OutputArray  mask = cv::noArray() //use only non-zero pts
);

输入矩阵 srcPoints 和 dstPoints 分别包含原始平面和目标平面中的点。
输入变量method用于决定计算单应性矩阵所使用的算法。如果使用默认值0，则会考虑所有点，计算结果会使冲投影的误差最小。在这种情况下，重投影误差是H乘以原始点与目标点之间的欧氏距离的平方和。
最后返回值为3X3矩阵。因为单应矩阵只有8个自由参数，我们进行标准化使 $H_{33} =1$ 。

透视变换

在计算单应矩阵之后，就可以吧一幅图像的点转移到另一幅图像上。实际上，图像中的每一个像素都可以转移，因此可以把整幅图像迁移到另一幅图像的视点上。这个过程称之为图像的拼接。

void cv::warpPerspective(
	cv::InputArray src,//input image
	cv::OutputArray dst,//output image that has the size dsize and the same type as src
	cv::InputArray M,//3X3 transformation matrix
	cv::Size dsize,//size of the output image
	int  flags = INTER_LINEAR,//
	..
);

填充多边形

void fillConvexPoly(
	cv::Mat&     Img,       //Image to be drawn on
	const cv::Point*  pts,  //C-style array of points
	int  npts,              //Number of points in 'pts'
	const cv::Scalar& color,//Color , from RGB
	int  lintType = 8,      //Connectedness, 4 or 8
	int  shift = 0          //Bits of radius to treat as fraction
);

pts中的点将被按顺序用直线段连接起来，第一个点和最后一个点之间也会连起来。就是封闭的图形。

注意，在使用函数时，由于const cv::Point* pts 需将该位置设置为指针。
Point *ptr; 或者 Point ptr[n]。但是由于前者没有给定的内存空间，不知道指针指向的位置，可能会产生越界错误。最好是用数组，越界与否都会显示。

step

#include "opencv2/core/mat.hpp"
step:矩阵元素对应的字节数
step[0]:矩阵第一行元素的字节数
step[1]:矩阵中一个元素的字节数
step[i]：三维矩阵i = 2 1 0，分别对应点、线、面，二维矩阵i =1 0，分别对应点、线

step1:矩阵元素对应的通道数
step1(0):矩阵中一行有几个通道数
step1(1):一个元素有几个通道数(channel())
同step

int main() {
    Mat img(3, 4, CV_16UC4, Scalar_<uchar>(1, 2, 3, 4));
    cout << "step:" << img.step << endl;
    cout << "step[0]:" << img.step[0] << endl;
    cout << "step[1]:" << img.step[1] << endl;
    cout << "step1(0):" << img.step1(0) << endl;
    cout << "step1(1):" << img.step1(1) << endl;
}

step:32
step[0]:32
step[1]:8
step1(0):16
step1(1):4

fastAtan2

float cv::fastAtan2	(	float 	y,
						float 	x )

Calculates the angle of a 2D vector in degrees.
The function fastAtan2 calculates the full-range angle of an input 2D vector. The angle is measured in degrees and varies from 0 to 360 degrees. The accuracy is about 0.3 degrees.

Parameters
x x-coordinate of the vector.
y y-coordinate of the vector.

Eigen

http://eigen.tuxfamily.org/dox/
有时候关于Eigen的报错，试着将争取版本的Eigen 安装之后，加上sudo make install可能会解决问题。原因的话，看Sophus

查看Eigen版本号：
在/usr/include/eigen3/Eigen/src/Core/util/Macros.h显示为3.3.4

头文件

CMakeLists

include_directories(/usr/include/eigen3)

Eigen用纯头文件搭建的库，没有二进制文件，不需要链接库文件target_link_libraries()

示例

#include "Eigen/"下的

头文件	作用
Core/	核心部分
Dense/	稠密矩阵的代数运算（逆、特征值等）
Geometry	旋转

Eigen中旋转的相互转化

角轴/旋转向量

AngleAxisd R (M_PI/2, Vector3d(0,0,1));//angle axis的顺序 z轴旋转90度

SVD分解
$E=U\Sigma V^T$

Matrix3d E;//待分解矩阵
JacobiSVD<Matrix3d> svd(E, ComputeFullU | ComputerFullV);//分解
Matrix U = svd.matrixU(), V = svd.matrixV();
Vector3d singlar_values = svd.singularValues();//Sigma matrix singlar values

DiagonalMatrix<double, 3> sing_matrix1( singlar_value[0],singlar_value[1],singlar_value[2]);//对角矩阵形式1
Matrix3d sing_matrix2 = singlar_values.asDiagonal();//对角矩阵形式2
cout << sing_matrix.diagonal();//输出对角

Isometry矩阵

Eigen::Isometry3d T = Eigen::Isometry3d::Identity();//初始化
T.rotate( rotation_vector	);
T.pretranslate( vector );
cout << T.matrix() << T.rotation()<< T.translation();

四元数

四元数不能直接乘以系数

Quaterniond q(1,2,3,4);
Quaterniond q1 = 2 * q;//会报错
Vector4d p;
p << q.x(), q.y(), q.z(), q.w();
Vector4d p1 = 2 * p;

注意

四元数q的归一化有两个函数normalize()和normalized()。前者将四元数归一化之后，可以直接使用此四元数q；后者只能使用q.normailzed()代替q。

Sophus

需知

该库是基于Eigen开发的，不需要安装额外的依赖库。只需编译，无需安装。
基于模板的Sophus与Eigen一样，仅含头文件而没有源文件。
SLAM十四讲第一版用的sophus是非模板，第二版用的是模板类。模板类是基于eigen3.2.92版本，非模板是基于eigen3.3.7。虽然书上说Sophus不用安装，但是有时程序会找不到头文件，还是需要sudo make install。find_package是寻找SophusConfig.cmake文件，此文件说明了你的Sophus库安装在哪里，如果只是make了，没有make install，那把Sophus的目录就放在当前项目根目录中，这个工程中的find_package会在当前目录中找这个配置文件。
当系统既安装了模板类，也安装了非模板类的Sophus时，在使用模板类时，正常写出CMakelists即可，而使用非模板类时，需将target_link_libraries中的${Sophus_LIBRARIES}改为具体路径，如/usr/local/lib/libSophus.so等（在Sophus非模板的源文件中，找到SophusConfig.cmake中，对应的${Sophus_LIBRARIES}变量即可）

模板类头文件后缀为hpp

find_package(Sphus REQUIRED)
include_directories(${Sophus_INCLUDE_DIRS})

示例

  // To be specific, this function computes ``vee(logmat(.))`` with
  // ``logmat(.)`` being the matrix logarithm and ``vee(.)`` the vee-operator
  // of SE(3).
  //
  SOPHUS_FUNC Tangent log() const

log()对数映射包含了 vee运算。而且要对应好群和代数的关系（vee hat 是非矩阵和项链的转化，不是群和代数的转换）。

Pangolin

需知

一个基于OpenGL的Pangolin库，它在支持OpenGL的绘图基础操作上还提供了一些GUI功能。

CMakeLists

find_package( Pangolin)
include_directoies( ${Pangolin_INCLUDE_DIRS})

...
target_link_libraries(${PROJECT_NAME} ${Pangolin_LIBRARIES})

PCL - Point Cloud Library

需知

http://pointclouds.org/documentation/

说明

find_package(PCL REQUIRED)
include_directories(${PCL_INCLUDE_DIRS})
add_definitions(${PCL_DEFINITIONS})
link_libraries( ${PCL_LIBRARY_DIRS})

target_link_libraries(${PROJECT_NAME} ${PCL_LIBRARIES})

所谓的点云Point Cloud 就是由一组离散的点表示的地图。最基本的点包含x,y,z三维坐标，也可以带有r,g,b彩色信息。根据RGB-D相机提供了彩色图和深度图，因此很容易根据相机内参来计算点云。
优点

可以表达物体的空间轮廓和具体位置
点云本身和视角无关，可以任意旋转。不同点云在同一坐标系下就可以直接融合

缺点

点云的分辨率和相机的距离有关。点云放大了，只是一个点，看不到具体信息，不同于像素
点云并不是稠密的表达，一般为稀疏表达。会使信息缺失

由于点云输出的稀疏地图放大就相当于一个个离散空间，通过网格化，可以将点变成稠密（相对于前面的离散点是连续）的网格。

网格主要用于计算机图形学中，有三角、四角网格等很多种，不过计算机图形学中网格的处理大多数是基于三角网格的。三角网格的优点：稳定性强；三角网格比较简单（主要原因），实际上三角网格是最简单的网格类型之一，可以非常方便并且快速生成，在非结构化网格中最常见，而且相对于一般多边形网格，许多操作对三角网格更容易；有助于恢复模型的表面细节。

三角网格在空间中的表示：

顶点。每个三角形都有三个顶点，各顶点都有可能和其他三角形共享。
边。连接两个顶点的边，每个三角形有三条边。
面。每个三角形对应一个面，我们可以用顶点或边列表表示面。

点云网格化输入是点云，输出是三维网格。
但输入的三维点云存在的问题

点云噪声。每个点云都会带有噪声，噪声有可能和物体表面光学性质、物体深度、传感器性能等都有关系。
点云匹配误差。三维重建中需要将不同帧得到的点云估计其在世界坐标系下的位姿，会引入一定的位置误差。
点云分布。分布的不均匀性体现在两个方面。一个是每个点云在不同的方向上分布是不均匀的另一个是不同的点云匹配后，不同位置的点云密度是不一样的。
缺失数据。扫描中如果碰到不易成像的部位（比如不可见、反光等等），那么这部分的数据是缺失的，点云是不完整的。

输出的网格需要具有的能力

对点云噪声有一定的冗余度。
能够重建出曲率变化比较大的曲面。
能够处理大数据量，算法时间和空间复杂度不会太高。
重建出的网格中包含尽可能少的异常三角片（三角片交错在一起、表面法向量不连续或不一致、同一个位置附近出现多层三角片等）。

网格生成一般分为两大类方法：

插值法。顾名思义，也就是重建的曲面都是通过原始的数据点得到的
逼近法。用分片线性曲面或其他曲面来逼近原始数据点，得到的重建曲面是原始点集的一个逼近。

网格化：第一步滤波，第二步是进行平滑（smoothing），第三步是估计点云的表面法线（normal），第四步是通过算法优化生成网格。

点云滤波
需要滤波的情况：点云数据密度不规则需要平滑、因遮挡等问题造成离群点需要滤除、大量数据需要下采样、噪声数据需要去除。滤波方案：按照给定的规则限制过滤去除点、通过常用滤波算法修改点的部分属性、对数据进行下采样。
数据下采样。由于点云的各个点都有深度值，可以转化为大量点组成的点云，但是并不是所有的点都是有效点。按照一定规则抽取具有代表性的样本，可以代替原来的样本。
离群点 Outliers 也叫外点，明显错误的点。离群点会使局部点云特征的估计复杂化，从而导致错误的值，导致点云配准失败。下采样和离群点处理可以累计叠加处理点云。

平滑估计
由于滤波之后，还会由于传感器的测量误差而产生的不规则数据，该数据直接用来曲面重建的话，会使重建的曲面不光滑或者有漏洞，而且这种不规则数据很难用统计分析等滤波方法进行消除。故为了建立光滑完整的模型必须对物体表面进行平滑处理和漏洞修复。

上述提到的不规则数据还有一种原因。在后处理过程中，对同一物体从不同方向进行多次扫描，然后把扫描结果进行配准，得到完整的模型。但由于每次配准的结果不准确，如会使一面墙变为两面墙。我们没有条件重新扫描出更精确的结果，或者配准精度也无法提升，可以通过重采样的方法来实现点云的平滑，从而避免出现这样的问题。

点云重采样，实际是用移动最小二乘（MLS,Moving Least Squares）来实现的。

估计表面法线
法线 normal 决定着曲面与光源（light source）的强弱处理（Flat Shading），对于每个点光源位置，其亮度取决于曲面法线的方向。
点云的法线计算有两种方法：使用曲面重建方法，从点云数据中得到采样点对应的曲面，然后再用曲面模型计算其表面的法线；直接使用近似值直接从点云数据集推断出曲面法线。
对于法二具体来说，就是把估计某个点的表面法线问题简化为：从该点最近邻计算的协方差矩阵的特征向量和特征值的分析。
需要从该点的周围点邻域（也称为k邻域）估计一点处的表面法线。K近邻的取值可以通过选择 $k$ 个最近点，或者确定一个以 $r$ 为半径的圆内的点集来确定。

点云贪心三角化原理
使用贪心投影三角化算法对有向点云进行三角化。该算法的优点是可以用来处理来自一个或者多个设备扫描、并且有多个连接处的散乱点云。但是也是有很大的局限性，它更适用于采样点云来自表面连续光滑的曲面，并且点云的密度变化比较均匀的情况。

算法流程

先将点云通过法线投影到某二维坐标平面内
然后对投影得到的点云做平面内的三角化，从而得到各点的拓扑连接关系，平面三角化的过程中用到了基于Delaunay三角剖分的空间区域增长算法
最后根据平面内投影点的拓扑连接关系确定各原始三维点间的拓扑连接，所得三角网格即为重建得到的曲面模型

第二步，通过选取一个样本三角片作为初始曲面，不断扩张延伸曲面的边界，直到所有符合几何正确性和拓扑正确性的点都被连上，最后形成一张完整的三角网格曲面。

Delaunay 三角剖分
点集的三角剖分对数值分析以及图形学来说，三角剖分都是极为重要的一项预处理技术。而Delaunay 三角剖分是一种常用的三角剖分的方法，这个方法比较常见，关于点集的很多种几何图都和Delaunay三角剖分相关，如Voronoi图。
Delaunay 三角剖分的有两个优点：最大化最小角，最接近于规则化的“三角网；唯一性（任意四点不能共圆）。
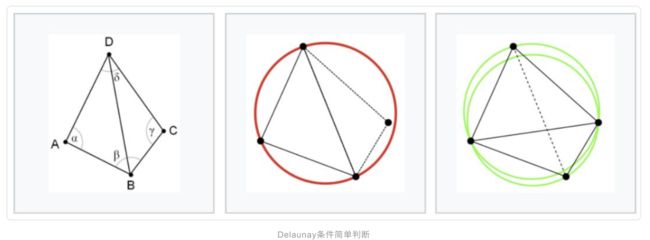
**公共边缘BD的两个三角形ABD和BCD，如果角度α和γ之和小于或等于180°，则三角形满足Delaunay条件。**按照这个标准下图左、中都不满足Delaunay条件，只有右图满足。

数据类型

K-d tree
由于点云数据表征为目标表面海量点的集合，并不具备传统实体网格数据的几何拓扑信息。因此点云数据处理中最为核心的问题就是建立离散点间的拓扑关系，实现基于邻域关系的快速查找。因此引入K-d tree数据结构。
K-d tree或者k维数用来组织表示k维空间中点的集合，是一种带有其他约束的二分查找树，对于区间和近邻搜索十分有用。点云中K-d tree为三维。
k-d tree的每一级在指定维度上分开所有的子节点。在树的根部所有子节点是以第一个指定的维度上被分开，（也就是说，如果第一维坐标小于根节点的点将它分在左边的子树中，如果大于根节点的点将它分在右边的子树中）。树的每一级都在下一个维度上分开，所有维度都用完之后，回到第一个维度。
建立K-d tree最高效的方法是，像快速分类一样使用分割法，把指定维度的值放在根上，在该维度上包含较小的值在左子树，较大的在右子树。然后分别在左边和右边的子树上重复这个过程，直到用户准备分类的最后一个树仅仅由一个元素组成。

PCL中K-d tree库提供了 K-d tree 数据结构，基于FLANN进行快速最近邻检索。
class pcl::search::KdTree

示例

点云的创建

点云用PointCloud::Ptr类型表示。

typedef pcl::PointXYZRGB PointT;
pcl::PointCloud<PointT>::Ptr newClouds ( new pcl::PointCloud<PointT> );

点云的转换

void pcl::transformPointCloud	(	
	const pcl::PointCloud< PointT > & 	cloud_in,// the input point cloud
	pcl::PointCloud< PointT > & 	cloud_out, // the resultant output point cloud
	const Eigen::Matrix< Scalar, 4, 4 > & 	transform, //a rigid transformation
	bool 	copy_all_fields = true 
)

Note : Can be used with cloud_in equal to cloud_out.

下采样

class pcl::ApproxmiateVoxelGrid< PointT >
用于对海量的点云在处理前进行数据压缩，并在特征提取等处理中选择合适的体素（Voxel，三维元素，对应二维的像素）大小等参数，提高算法效率。
该函数对输入的点云数据创建一个三维体素栅格，每个体素内用体素中所有点的重心来近似显示体素中其他点，这样该体素内所有点都用一个重心点最终表示。
优点是可以在下采样的时候保存点云的形状特性。

typedef pcl::PointXYZRGB PointT;
pcl::VoxelGrid<PointT> downSampled; //创建滤波对象
downSampled.setInputCloud (cloud); //设置需要过滤的点云给滤波对象

downSampled.setLeafSize (0.01f, 0.01f, 0.01f); //设置滤波时创建的体素体积为1cm的立方体
//分别表示体素在XYZ方向的尺寸，以米为单位

downSampled.filter (*cloud_downSampled); //执行滤波处理，存储输出

成员函数
setDownsampleAllData( bool downsample)设置是否对所有的字段进行下采样

离群点的去除

StatisticalOutlierRemoval 使用统计分析技术，从点云数据集中移除测量噪声点。对每个点的邻域进行统计分析，剔除不符合一定标准的邻域点。
具体来说，对于每个点，我们计算它到所有相邻点的平均距离。假设得到的分布是高斯分布，我们可以计算出一个均值 $\mu$ 和一个标准差 $\sigma$ ，那么这个邻域点集中所有点与其邻域距离大于 $\mu + std_{mul} * \sigma$ 区间之外的点都可以被视为离群点，并可从点云数据中去除。 $std_{mul}$ 是标准差倍数的一个阈值，可以自己指定。

typedef pcl::PointXYZRGB PointT;
pcl::StatisticalOutlierRemoval<pcl::PointXYZ> sor;   //创建滤波器对象
sor.setInputCloud (cloud);                           //设置待滤波的点云
sor.setMeanK (50);                               //设置在进行统计时考虑的临近点个数
sor.setStddevMulThresh (1.0);                      //设置判断是否为离群点的阀值，用来倍乘标准差，也就是上面的std_mul
sor.filter (*cloud_filtered);                    //滤波结果存储到cloud_filtered

RadiusOutlierRemoval 在点云数据中，设定每个点一定半径范围内周围至少有足够多的近邻，不满足就会被删除。半径是通过计算某个点和它周围所有点的欧氏距离，都是以米为单位的，可以直接指定具体的数值。

typedef pcl::PointXYZRGB PointT;
pcl::RadiusOutlierRemoval<pcl::PointXYZ> pcFilter;  //创建滤波器对象
pcFilter.setInputCloud(cloud);             //设置待滤波的点云
pcFilter.setRadiusSearch(0.8);               // 设置搜索半径
pcFilter.setMinNeighborsInRadius(2);      // 设置一个内点最少的邻居数目（见上面解释）
pcFilter.filter(*cloud_filtered);        //滤波结果存储到cloud_filtered

离群点的显示

typedef pcl::PointXYZRGB PointT;
pcl::PointCloud<PointT>::Ptr noise(new pcl::PointCloud<PointT>);

//呈上各个算法
***.setNegative(true);
***.filter(*noise);

移动最小二乘

template <typename PointInT, typename PointOutT>//输入类型PointInT 输出类型PointOutT
class MovingLeastSquares: public CloudSurfaceProcessing<PointInT, PointOutT>

实践

// 对点云重采样  
pcl::search::KdTree<PointT>::Ptr treeSampling (new pcl::search::KdTree<PointT>); // 创建用于最近邻搜索的KD-Tree
pcl::PointCloud<PointT> mls_points;   //输出MLS
pcl::MovingLeastSquares<PointT, PointT> mls;  // 定义最小二乘实现的对象mls
mls.setComputeNormals (false);  //设置在最小二乘计算中是否需要存储计算的法线
mls.setInputCloud (cloud_filtered);        //设置待处理点云
mls.setPolynomialOrder(2);             // 拟合2阶多项式拟合 PolynomialOrder多项式阶次
mls.setPolynomialFit (false);  // 设置为false可以 加速 smooth PolynomialFit多项式拟合
mls.setSearchMethod (treeSampling);    // 设置KD-Tree作为搜索方法
mls.setSearchRadius (0.05); // 单位m.设置用于拟合的K近邻半径
mls.process (mls_points);        //输出

法线的估计

pcl::PointCloud<pcl::Normal>::Ptr normals (new pcl::PointCloud<pcl::Normal>); 
//pcl::Normal ：A point structure representing normal coordinates and the surface curvature estimate.
...
template <typename PointInT, typename PointOutT>//输入类型PointInT 输出类型PointOutT
class NormalEstimation: public Feature<PointInT, PointOutT>

实践

// 法线估计
pcl::NormalEstimation<PointT, pcl::Normal> normalEstimation;                    //创建法线估计的对象
normalEstimation.setInputCloud(cloud_smoothed);                                    //输入点云
pcl::search::KdTree<PointT>::Ptr tree(new pcl::search::KdTree<PointT>);          // 创建用于最近邻搜索的KD-Tree
normalEstimation.setSearchMethod(tree);
pcl::PointCloud<pcl::Normal>::Ptr normals (new pcl::PointCloud<pcl::Normal>);     // 定义输出的点云法线

// K近邻确定方法，使用k个最近点，或者确定一个以r为半径的圆内的点集来确定都可以，两者选1即可
normalEstimation.setKSearch(10);                    // 使用当前点周围最近的10个点
//normalEstimation.setRadiusSearch(0.03);            //对于每一个点都用半径为3cm的近邻搜索方式
normalEstimation.compute(*normals);                 //计算法线

贪心投影三角化

pcl::PointCloud<pcl::PointNormal>::Ptr cloud_with_normals(new pcl::PointCloud<pcl::PointNormal>);
//pcl::PointNormal: A point structure representing Euclidean xyz coordinates,
//                 together with normal coordinates and the surface curvature estimate.


template <typename PointIn1T, typename PointIn2T, typename PointOutT> void
pcl::concatenateFields (const pcl::PointCloud<PointIn1T> &cloud1_in,
                        const pcl::PointCloud<PointIn2T> &cloud2_in,
                        pcl::PointCloud<PointOutT> &cloud_out)

实践

// 将点云位姿、颜色、法线信息连接到一起
pcl::PointCloud<pcl::PointNormal>::Ptr cloud_with_normals(new pcl::PointCloud<pcl::PointNormal>);
pcl::concatenateFields(*cloud_smoothed, *normals, *cloud_with_normals);

//定义搜索树对象
pcl::search::KdTree<pcl::PointNormal>::Ptr tree2(new pcl::search::KdTree<pcl::PointNormal>);
tree2->setInputCloud(cloud_with_normals);

// 三角化
pcl::GreedyProjectionTriangulation<pcl::PointNormal> gp3;   // 定义三角化对象
pcl::PolygonMesh triangles; //存储最终三角化的网络模型 Polygon多边形 Mesh网格

// 设置三角化参数
gp3.setSearchRadius(0.1);  //设置搜索时的半径，也就是KNN的球半径
gp3.setMu (2.5);  //设置样本点搜索其近邻点的最远距离为2.5倍（典型值2.5-3），这样使得算法自适应点云密度的变化
gp3.setMaximumNearestNeighbors (100);    //设置样本点最多可搜索的邻域个数，典型值是50-100

gp3.setMinimumAngle(M_PI/18); // 设置三角化后得到的三角形内角的最小的角度为10°
gp3.setMaximumAngle(2*M_PI/3); // 设置三角化后得到的三角形内角的最大角度为120°

gp3.setMaximumSurfaceAngle(M_PI/4); // 设置某点法线方向偏离样本点法线的最大角度45°，如果超过，连接时不考虑该点
gp3.setNormalConsistency(false);  //设置该参数为true保证法线朝向一致，设置为false的话不会进行法线一致性检查

gp3.setInputCloud (cloud_with_normals);     //设置输入点云为有向点云
gp3.setSearchMethod (tree2);   //设置搜索方式
gp3.reconstruct (triangles);  //重建提取三角化

其中setMaximumSurfaceAngle和setNormalConsistency 其实是用于处理有尖锐边缘或棱角的情况，以及表面的两面非常接近的情况。setNormalConsistency，注释里也说了，是保证法线朝向一致。因为大多数表面法线估计方法得到的法线，即使是在锐利的边缘之间也是平滑的过渡。因为不是所有的法线估计方法都能保证法线的方向一致。通常情况下，设置为false对大多数数据集有效

输出点云文件

pcl::io::savePCDFile ("./***.pcd", *cloud_name);
终端通过pcl_viewer ***.pcd查看生成的点云。

Save point cloud data to a PCD file containing n-D points

template<typename PointT> inline int
write (const std::string &file_name, //file_name the output file name
       const pcl::PointCloud<PointT> &cloud, //cloud the pcl::PointCloud data
       const bool binary = false //binary set to true if the file is to be written in a binary
             )
    {
    if (binary)
        return (writeBinary<PointT> (file_name, cloud));
      else
        return (writeASCII<PointT> (file_name, cloud));
    }

pcl::PCDWriter writer;
writer.write<PointT> ("***.pcd", *cloud_name, false);

    boost::shared_ptr<pcl::visualization::PCLVisualizer> viewer(new pcl::visualization::PCLVisualizer("3D Viewer"));
    viewer->setBackgroundColor(0, 0, 0);
    pcl::visualization::PointCloudColorHandlerRGBField<PointT> rgb(cloud_name);
    viewer->addPointCloud<PointT> (cloud_name, rgb, "sample cloud");
    while (!viewer->wasStopped())
    {
        viewer->spinOnce(100);
        boost::this_thread::sleep(boost::posix_time::microseconds(100000));
    }
	return (0);

直接输出点云。
boost::share_ptr是智能指针，可以共享所有权的指针。如果有多个shared_ptr共同管理同一子个对象时，只有这些shared_ptr全部与该对象脱离关系之后，被管理的对象才会被自动释放。

图优化 g2o

图优化：graph optimization or graph-based optimization
g2o： General Graph Optimization
图优化，属于非线性优化，是把优化问题表现成图（图论的概念）的一种方式。一个图由若干个顶点Vertex，以及链接这些顶点的边Edge组成。用顶点表示优化变量，用边表示误差项。于是，对任意一个最小二乘问题可以构建一个与之对应的一个图。

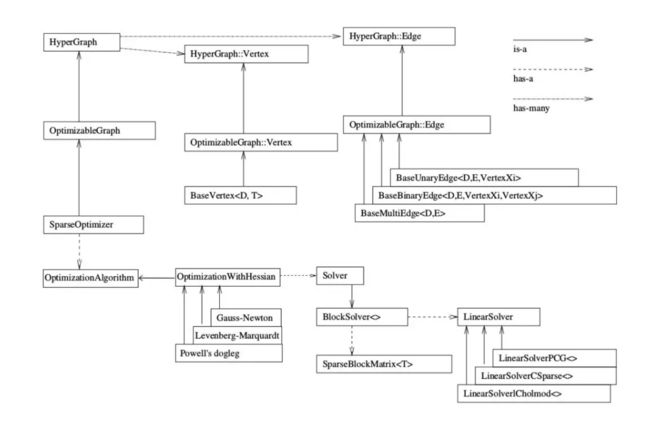
g2o的基本框架结构

示例

求解器

如何求解：OptimizationWithHessian 内部包含一个求解器（Solver），这个Solver实际是由一个BlockSolver组成的。这个BlockSolver有两个部分，一个是SparseBlockMatrix ，用于计算稀疏的雅可比和Hessian矩阵；一个是线性方程的求解器（LinearSolver），它用于计算迭代过程中最关键的一步 $H\Delta x=−b$ ，LinearSolver有几种方法可以选择：PCG, CSparse, Choldmod。

求解顺序
LinearSolver->BlockSolver<>->Solver->SparseOptimizer->HyperGraph

typedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block;  // 每个误差项优化变量维度为3，误差值维度为1

// 第1步：创建一个线性求解器LinearSolver
//invalid: Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense(); 
std::unique_ptr<Block::LinearSolverType> linearSolver ( new g2o::LinearSolverDense<Block::PoseMatrixType>());

// 第2步：创建BlockSolver。并用上面定义的线性求解器初始化
//invalid: Block* solver_ptr = new Block( linearSolver );      
std::unique_ptr<Block> solver_ptr ( new Block ( std::move(linearSolver)));

// 第3步：创建总求解器solver。并从GN, LM, DogLeg 中选一个，再用上述块求解器BlockSolver初始化
//invalid    g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr );
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( std::move(solver_ptr) );
// g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( std::move(solver_ptr) );
// g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( std::move(solver_ptr) );

// 第4步：创建终极大boss 稀疏优化器（SparseOptimizer）
g2o::SparseOptimizer optimizer;     // 图模型
optimizer.setAlgorithm( solver );   // 设置求解器
optimizer.setVerbose( true );       // 打开调试输出

// 第5步：定义图的顶点和边。并添加到SparseOptimizer中
CurveFittingVertex* v = new CurveFittingVertex(); //往图中增加顶点
v->setEstimate( Eigen::Vector3d(0,0,0) );
v->setId(0);
optimizer.addVertex( v );

for ( int i=0; i<N; i++ )    // 往图中增加边
{
  CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] );
  edge->setId(i);
  edge->setVertex( 0, v );                // 设置连接的顶点
  edge->setMeasurement( y_data[i] );      // 观测数值
  edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵：协方差矩阵之逆
  optimizer.addEdge( edge );
}

// 第6步：设置优化参数，开始执行优化
optimizer.initializeOptimization();
optimizer.optimize(100);

具体步骤

对增量方程的求解 $H\Delta x=−b$ ，创建一个线性求解器LinearSolver

LinearSolverCholmod ：使用sparse cholesky分解法。继承自LinearSolverCCS
LinearSolverCSparse：使用CSparse法。继承自LinearSolverCCS
LinearSolverPCG ：使用preconditioned conjugate gradient 法，继承自LinearSolver
LinearSolverDense ：使用dense cholesky分解法。继承自LinearSolver
LinearSolverEigen： 依赖项只有eigen，使用eigen中sparse Cholesky 求解，因此编译好后可以方便的在其他地方使用，
//性能和CSparse差不多。继承自LinearSolver

创建BlockSolver。并用上面定义的线性求解器初始化。
BlockSolver 内部包含 LinearSolver，用上面我们定义的线性求解器LinearSolver来初始化。它的定义在如下文件夹内 g2o/g2o/core/block_solver.h

BlockSolver:
//其中p代表pose的维度（注意一定是流形manifold下的最小表示），l表示landmark的维度
using BlockSolverPL = BlockSolver< BlockSolverTraits<p, l> >;
//可变尺寸的solver
using BlockSolverX = BlockSolverPL<Eigen::Dynamic, Eigen::Dynamic>;

//预定义的类型
BlockSolver_6_3 ：表示pose 是6维，观测点是3维。用于3D SLAM中的BA
BlockSolver_7_3：在BlockSolver_6_3 的基础上多了一个scale
BlockSolver_3_2：表示pose 是3维，观测点是2维

创建总求解器solver
g2o/g2o/core/

g2o::OptimizationAlgorithmGaussNewton
g2o::OptimizationAlgorithmLevenberg 
g2o::OptimizationAlgorithmDogleg

创建终极大boss 稀疏优化器（SparseOptimizer），并用已定义求解器作为求解方法。
创建稀疏优化器g2o::SparseOptimizer optimizer;
用前面定义好的求解器作为求解方法：SparseOptimizer::setAlgorithm(OptimizationAlgorithm* algorithm)
其中setVerbose是设置优化过程输出信息用的SparseOptimizer::setVerbose(bool verbose)
定义图的顶点和边，并添加到SparseOptimizer中
设置优化参数，开始执行优化
设置SparseOptimizer的初始化、迭代次数、保存结果等。
初始化SparseOptimizer::initializeOptimization(HyperGraph::EdgeSet& eset)
设置迭代次数，然后就开始执行图优化了。SparseOptimizer::optimize(int iterations, bool online)

设置顶点

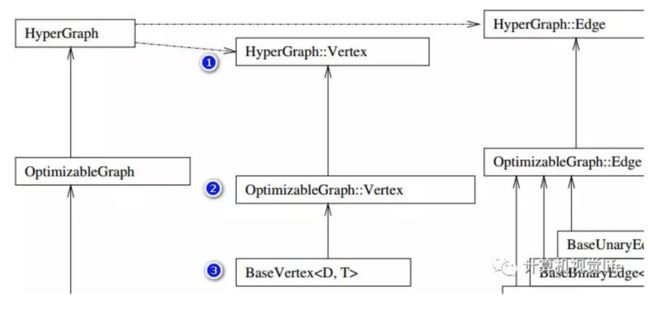
顶点Vertex参数

/* Templatized BaseVertex
 * D  : minimal dimension of the vertex, e.g., 3 for rotation in 3D. -1 means dynamically assigned at runtime.
 * T  : internal type to represent the estimate, e.g., Quaternion for rotation in 3D
 */
template <int D, typename T>
class BaseVertex : public OptimizableGraph::Vertex {
...
...
static const int Dimension = D; ///< dimension of the estimate (minimal) in the manifold space

可以看到这个D并非是顶点（更确切的说是状态变量）的维度，而是其在流形空间（manifold）的最小表示，这里一定要区别开，另外，源码里面也给出了T的作用

typedef T EstimateType;
EstimateType _estimate;

可以看到，这里T就是顶点（状态变量）的类型，跟前面一样。

定义顶点
可以自定义顶点或者使用给定的顶点。

给定顶点

VertexSE2 : public BaseVertex<3, SE2>  //2D pose Vertex, (x,y,theta)
VertexSE3 : public BaseVertex<6, Isometry3>  //6d vector (x,y,z,qx,qy,qz)
// (note that we leave out the w part of the quaternion)
VertexPointXY : public BaseVertex<2, Vector2>
VertexPointXYZ : public BaseVertex<3, Vector3>
VertexSBAPointXYZ : public BaseVertex<3, Vector3>

// SE3 Vertex parameterized internally with a transformation matrix and externally with its exponential map
VertexSE3Expmap : public BaseVertex<6, SE3Quat>

// SBACam Vertex, (x,y,z,qw,qx,qy,qz),(x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion.
// qw is assumed to be positive, otherwise there is an ambiguity in qx,qy,qz as a rotation
VertexCam : public BaseVertex<6, SBACam>

// Sim3 Vertex, (x,y,z,qw,qx,qy,qz),7d vector,(x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion.
VertexSim3Expmap : public BaseVertex<7, Sim3>

复杂点例子：李代数表示位姿VertexSE3Expmap
g2o/types/sba/types_six_dof_expmap.h

/**

 \* \brief SE3 Vertex parameterized internally with a transformation matrix

 and externally with its exponential map

 */

class G2O_TYPES_SBA_API VertexSE3Expmap : public BaseVertex<6, SE3Quat>{
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW
  VertexSE3Expmap();
  bool read(std::istream& is);
  bool write(std::ostream& os) const;
  virtual void setToOriginImpl() {
    _estimate = SE3Quat();
  }

  virtual void oplusImpl(const number_t* update_)  {
    Eigen::Map<const Vector6> update(update_);
    setEstimate(SE3Quat::exp(update)*estimate());        //更新方式
  }
};

第一个参数6 表示内部存储的优化变量维度，这是个6维的李代数
第二个参数是优化变量的类型，这里使用了g2o定义的相机位姿类型：SE3Quat。

三维点的例子，空间点位置 VertexPointXYZ，维度为3，类型是Eigen的Vector3

class G2O_TYPES_SBA_API VertexSBAPointXYZ : public BaseVertex<3, Vector3>
{
  public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW    
    VertexSBAPointXYZ();
    virtual bool read(std::istream& is);
    virtual bool write(std::ostream& os) const;
    virtual void setToOriginImpl() {
      _estimate.fill(0);
    }

    virtual void oplusImpl(const number_t* update)
    {
      Eigen::Map<const Vector3> v(update);
      _estimate += v;
    }
};

自定义顶点
重定义顶点一般重写以下函数

virtual bool read(std::istream& is);
virtual bool write(std::ostream& os) const;
virtual void oplusImpl(const number_t* update);
virtual void setToOriginImpl();

read，write：分别是读盘、存盘函数，一般情况下不需要进行读/写操作的话，仅仅声明一下就可以
setToOriginImpl：顶点重置函数，设定被优化变量的原始值。
oplusImpl：顶点更新函数。非常重要的一个函数，主要用于优化过程中增量 $\Delta x$ 的计算。我们根据增量方程计算出增量之后，就是通过这个函数对估计值进行调整的，因此这个函数的内容一定要重视。

曲线模型的顶点，模板参数：优化变量维度和数据类型

class myVertex: public g2o::BaseVertex<Dim, Type>
  {
      public:
      EIGEN_MAKE_ALIGNED_OPERATOR_NEW//new的对齐版本重载
      
      myVertex(){}

      virtual void setToOriginImpl() //重置
      {
          _estimate = Type();
      }
      virtual void oplusImpl(const double* update) override //更新
      {
          _estimate += /*update*/;
      }

      virtual bool read(std::istream& is) {}
      virtual bool write(std::ostream& os) const {}
  }

使用顶点

//初始化第一个顶点
myVertex* pose = new myVertex();
pose->setId(0);
pose->setEstimate(chushihua);
optimizer.addVertex(pose);

//读入顶点
int index = 1;
for( auto &i : ..){
g2o::VertexSBAPointXYZ* point (new g2o::VertexSBAPointXYZ());
point->setId(index++);
point->setEstimate(Eigen::Vector3d(i.x, i.y, i.z));
point->setMarginalized(true);
optimizer.addVertex(point);
}

设置边

g2o/g2o/core/hyper_graph.h g2o/g2o/core/optimizable_graph.h g2o/g2o/core/base_edge.h
BaseUnaryEdge，BaseBinaryEdge，BaseMultiEdge 分别表示一元边，两元边，多元边。一元边理解为一条边只连接一个顶点，两元边理解为一条边连接两个顶点，多元边理解为一条边可以连接多个（3个以上）顶点。

边定义类型的参数
D 是 int 型，表示测量值的维度（dimension）
E 表示测量值的数据类型
VertexXi，VertexXj 分别表示不同顶点的类型
边表示三维点投影到图像平面的重投影误差，就可以设置输入参数如下：
BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>:2表示测量值为2维，也就是图像像素坐标的差值，对应测量值的类型为Vector2D，两个顶点也就是优化变量分别为三维点VertexSBAPointXYZ和李群位姿VertexSE3Expmap。

边重要的成员函数

//分别是读盘、存盘函数，一般情况下不需要进行读/写操作的话，仅仅声明一下就可以
virtual bool read(std::istream& is);
virtual bool write(std::ostream& os) const;

//使用当前顶点的值计算的测量值与真实的测量值之间的误差
virtual void computeError();

//在当前顶点的值下，该误差对优化变量的偏导数，也就是我们说的Jacobian
virtual void linearizeOplus();

其他成员函数

_measurement//存储观测值
_error//存储computeError() 函数计算的误差
_vertices[]//存储顶点信息，比如二元边的话，_vertices[] 的大小为2，
//存储顺序和调用setVertex(int, vertex) 是设定的int 有关（0 或1）
setId(int)//来定义边的编号（决定了在H矩阵中的位置）
setMeasurement(type) //函数来定义观测值
setVertex(int, vertex) //来定义顶点
setInformation()// 来定义信息矩阵（协方差矩阵的逆）

自定义边

class myEdge: public g2o::BaseBinaryEdge<errorDim, errorType, Vertex1Type, Vertex2Type>
  {
      public:
      EIGEN_MAKE_ALIGNED_OPERATOR_NEW      
      myEdge(){}     
      virtual bool read(istream& in) {}
      virtual bool write(ostream& out) const {}      
      virtual void computeError() override
      {
          // ...
          _error = _measurement - Something;
      }      
      virtual void linearizeOplus() override
      {
          _jacobianOplusXi(pos, pos) = something;
          // ...         
          /*
          _jocobianOplusXj(pos, pos) = something;
          ...
          */
      }      
      private:
      // data
  }

一元边：主要是定义误差函数

// 误差模型 模板参数：观测值维度，类型，连接顶点类型
class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}
    // 计算曲线模型误差
    void computeError()
    {
        const CurveFittingVertex* v = static_cast<const CurveFittingVertex*> (_vertices[0]);
        const Eigen::Vector3d abc = v->estimate();
        _error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ) ;
    }
    virtual bool read( istream& in ) {}
    virtual bool write( ostream& out ) const {}
public:
    double _x;  // x 值， y 值为 _measurement
};

二元边：3D-2D点的PnP 问题，也就是最小化重投影误差问题
g2o/types/sba/types_six_dof_expmap.h

//继承了BaseBinaryEdge类，观测值是2维，类型Vector2D,顶点分别是三维点、李群位姿
class G2O_TYPES_SBA_API EdgeProjectXYZ2UV : public  BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>{
  public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
    //1. 默认初始化
    EdgeProjectXYZ2UV();
    //2. 计算误差
    void computeError()  {
      //李群相机位姿v1
      const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[1]);
      // 顶点v2
      const VertexSBAPointXYZ* v2 = static_cast<const VertexSBAPointXYZ*>(_vertices[0]);
      //相机参数
      const CameraParameters * cam
        = static_cast<const CameraParameters *>(parameter(0));
     //误差计算，测量值减去估计值，也就是重投影误差obs-cam
     //估计值计算方法是T*p,得到相机坐标系下坐标，然后在利用camera2pixel()函数得到像素坐标。
      Vector2D obs(_measurement);
      _error = obs-cam->cam_map(v1->estimate().map(v2->estimate()));
    }
    //3. 线性增量函数，也就是雅克比矩阵J的计算方法
    virtual void linearizeOplus();
    //4. 相机参数
    CameraParameters * _cam; 
    bool read(std::istream& is);
    bool write(std::ostream& os) const;
};

其中_error = obs - cam->cam_map(v1->estimate().map(v2->estimate()));就是 $误差 = 观测 - 投影$ 。
g2o/types/sba/types_six_dof_expmap.cpp:cam_map把相机坐标系下三维点（输入）用内参转换为图像坐标（输出）

Vector2  CameraParameters::cam_map(const Vector3 & trans_xyz) const {
  Vector2 proj = project2d(trans_xyz);
  Vector2 res;
  res[0] = proj[0]*focal_length + principle_point[0];
  res[1] = proj[1]*focal_length + principle_point[1];
  return res;
}

g2o/types/sim3/sim3.h:map函数是把世界坐标系下三维点变换到相机坐标系

Vector3 map (const Vector3& xyz) const {
        return s*(r*xyz) + t;
}

因此v1->estimate().map(v2->estimate())用v1估计的pose把v2代表的三维点，变换到相机坐标系下。

向图中添加边
一元边

// 往图中增加边
for ( int i=0; i<N; i++ )
    {
        CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] );
        edge->setId(i);
        edge->setVertex( 0, v );                // 设置连接的顶点
        edge->setMeasurement( y_data[i] );      // 观测数值
        edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵：协方差矩阵之逆
        optimizer.addEdge( edge );
}

二元边：需要用边连接两个顶点

index = 1;
for ( const Point2f p:points_2d )
 {
        g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();
        edge->setId ( index );
        edge->setVertex ( 0, dynamic_cast<g2o::VertexSBAPointXYZ*> ( optimizer.vertex ( index ) ) );
        edge->setVertex ( 1, pose );
        edge->setMeasurement ( Eigen::Vector2d ( p.x, p.y ) );
        edge->setParameterId ( 0,0 );
        edge->setInformation ( Eigen::Matrix2d::Identity() );
        optimizer.addEdge ( edge );
        index++;
}

setVertex：

// set the ith vertex on the hyper-edge to the pointer supplied
void setVertex(size_t i, Vertex* v) { 
	assert(i < _vertices.size() && "index out of bounds"); 
	_vertices[i]=v;}

g2o/core/hyper_graph.h：g2o::EdgeProjectXYZ2UV

class G2O_TYPES_SBA_API EdgeProjectXYZ2UV 
.....
 //李群相机位姿v1
const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[1]);
// 顶点v2
const VertexSBAPointXYZ* v2 = static_cast<const VertexSBAPointXYZ*>(_vertices[0]);

_vertices[0] 对应的是 VertexSBAPointXYZ 类型的顶点，也就是三维点，_vertices[1] 对应的是VertexSE3Expmap 类型的顶点，也就是位姿pose。因此前面 1 对应的就应该是 pose，0对应的应该就是三维点。

OpenCV Eigen Sophus PCL G2O

外用库学习笔记

OpenCV

需知

OpenCV的结构

OpenCV modules

头文件

数据类型

示例

显示图片

视频

从摄像头中读取

读取文件并存放

读取配置文件

保存图片到文件

图像的像素

绘图

随机选择颜色

取整函数

关键点和描述子

对极几何

计算极线

单应函数

透视变换

填充多边形

step

fastAtan2

Eigen

头文件

示例

Eigen中旋转的相互转化

注意

Sophus

需知

示例

Pangolin

需知

PCL - Point Cloud Library

需知

说明

数据类型

示例

点云的创建

点云的转换

下采样

离群点的去除

离群点的显示

移动最小二乘

法线的估计

贪心投影三角化

输出点云文件

图优化 g2o

g2o的基本框架结构

示例

求解器

设置顶点

设置边

你可能感兴趣的:(opencv)