Householder transformation + QL to calculate eigenValue and eigenVectors of Hertian Matrix, cpu code

化Hertinan matrix eigen problem into a real symmetric matrix eigen problem:

原理：

与matlab的结果进行对比：

A=[ ...
( 3.0 + 0.0*j) (-2.0   -2.0*j) (-0.9    -0.9*j) (-0.5    -0.5*j); ...
(-2.0 + 2.0*j) ( 4.0 +  0.0*j) ( 1.0 +   1.0*j) (-0.7    -0.5*j); ...
(-0.9 + 0.9*j) ( 1.0   -1.0*j) (-1.0 +   0.0*j) ( 0.1 +   0.1*j); ...
(-0.5 + 0.5*j) (-0.7 +  0.5*j) ( 0.1    -0.1*j) ( 1.0 +   0.0*j); ...
]

[V D]=eig(A)

#include 
#include 
#include 
#include 

using namespace std;
struct float2 {
	float x;
	float y;
};

typedef struct float2  float2;

void print_matrix(float* A, int M, int N, int lda);
void print_matrix_complex(float2* A, int M, int N, int lda);
void print_vector(float* A, int N);
/
void real_neimag_real_imag_fill(float2* A_h, int N, int lda, float* S, int n, int lds);
float max(float x, float y);
void swap(float& x, float& y);
void tred2(float* V, float* d, float* e, int n, int ldv);
void tql2(float* V, float* d, float* e, int n, int ldv);
void eigen_vector_decompose_hermitian(float2* A, int N, int lda, float2* V_cevd, float* d_cevd);
/

#define NA 4

/*
* complex A=(4x4)  math topology:
        ( 3.0,  0.0),  (-2.0,  -2.0),  (-0.9,  -0.9),  (-0.5,  -0.5),
        (-2.0,  2.0),  ( 4.0,   0.0),  ( 1.0,   1.0),  (-0.7,  -0.5),
        (-0.9,  0.9),  ( 1.0,  -1.0),  (-1.0,   0.0),  ( 0.1,   0.1),
        (-0.5,  0.5),  (-0.7,   0.5),  ( 0.1,  -0.1),  ( 1.0,   0.0)


float A_h[NA * (2*NA)] = {//complex columnMajor: mem topology
                                 3.0, 0.0,  -2.0, 2.0,  -0.9, 0.9,  -0.5,0.5,
                                -2.0,-2.0,   4.0, 0.0,   1.0,-1.0,  -0.7, 0.5,
                                -0.9,-0.9,   1.0, 1.0,  -1.0, 0.0,   0.1,-0.1,
                                -0.5,-0.5,  -0.7,-0.5,   0.1, 0.1,   1.0, 0.0

*/


int main() {

	float A_h[NA * (2 * NA)] = {//complex columnMajor:
								 3.0, 0.0,  -2.0, 2.0,  -0.9, 0.9,  -0.5, 0.5,
								-2.0,-2.0,   4.0, 0.0,   1.0,-1.0,  -0.7, 0.5,
								-0.9,-0.9,   1.0, 1.0,  -1.0, 0.0,   0.1,-0.1,
								-0.5,-0.5,  -0.7,-0.5,   0.1, 0.1,   1.0, 0.0
	};

///Parameters:
	int N = NA;
	int lda = N;
	float2* A = nullptr;
//___________________________________________________________________
	A = (float2*)malloc(lda * N * sizeof(float2));
	memcpy(A, A_h, lda * N * sizeof(float2));
	printf("A(ma)=\n");
	print_matrix_complex(A, N, N, N);
//______________________________________________________________

    //    void eigen_vector_decompose(float2 * A, int N, int lda, float2 * V_cevd, float* d_cevd);
    float* d_cevd = nullptr;
    float2* V_cevd = nullptr;
    int ldv_cevd = N;
    d_cevd = (float*)malloc(N * sizeof(float));
    V_cevd = (float2*)malloc(ldv_cevd * N * sizeof(float2));
    eigen_vector_decompose_hermitian(A, N, lda, V_cevd, d_cevd);


#if 0
	int n = 2 * N;
	int lds = n;
	float* S = nullptr;

	S = (float*)malloc(lds * n * sizeof(float));
	real_neimag_real_imag_fill((float2*)A, N, lda, S, n, lds);
	printf("S(ma)=\n");
	print_matrix(S, n, n, lds);
//______________________________________________________________

	int ldv_evd = n;
	float* V_evd = nullptr;

	V_evd = (float*)malloc(lds * n * sizeof(float));
	memcpy(V_evd, S, lds * n * sizeof(float));
	printf("V_evd(ma)=\n");
	print_matrix(V_evd, n, n, ldv_evd);

	float* e = nullptr;
	float* d_evd = nullptr;
	e = (float*)malloc(n * sizeof(float));
    d_evd = (float*)malloc(n * sizeof(float));

//______________________________________________________________
    //void tred2(float* V, float* e, float* d, int n, int ldv);
    tred2(V_evd, d_evd, e, n, ldv_evd);
    printf("V_evd-tred2=\n");
    print_matrix(V_evd, n, n, ldv_evd);
    printf("\nd-tred2=\n");
    print_vector(d_evd, n);
    printf("\ne-tred2=\n");
    print_vector(e, n);


    //void tql2(float* V, float* d, float* e, int n, int ldv);
    tql2(V_evd, d_evd, e, n, ldv_evd);
    printf("\nV_evd-tql2=\n");
    print_matrix(V_evd, n, n, ldv_evd);
    printf("\nd-tql2=\n");
    print_vector(d_evd, n);
    printf("\ne-tql2=\n");
    print_vector(e, n);
//_________________________________________________________________________________
    /**float* d_cevd = nullptr;
    float2* V_cevd = nullptr;

    int ldv_cevd = N;

    d_cevd = (float*)malloc(N * sizeof(float));
    V_cevd = (float2*)malloc(ldv_cevd * N * sizeof(float2));*/
    for(int i=0; i(RV[i][j2], RV[i + N][j2]);
            V_cevd[i + j * ldv_cevd].y = V_evd[(i + N) + j2 * ldv_evd];
        }
    }
    printf("\nV_cevd=\n");
    print_matrix_complex(V_cevd, N, N, ldv_cevd);


#endif

	return 0;
}


void real_neimag_real_imag_fill( float2 * A_h, int N, int lda, float* S, int n, int lds)//n=2*N
{
	float2 *A;
	A = A_h;
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			S[i +j*lds] = A[i+ j*lda].x;
			S[i +(j + N)*lds] = -A[i +j*lda].y;
			S[(i + N)+ j*lds] = -S[i +(j + N)*lds];
			S[(i + N)+ (j + N)*lds] = S[i+ j*lds];
		}
	}
}

//typedef float float;

void tred2(float *V, float* d, float *e, int n, int ldv)
{
    for (int j = 0; j < n; ++j)
        //LL::d[j] = V[n - 1][j];
        d[j] = V[(n - 1)+j*ldv];

    // Householder reduction to tridiagonal form
    for (int i = n - 1; i > 0; --i)
    {
        // scale to avoid under/overflow
        float scale = 0;
        float h = 0;

        for (int k = 0; k < i; ++k) {
         //   scale += fabs(d[k]);
            printf(" d[k]=%f", d[k]);
            scale += fabs(d[k]);
            printf(" scale=%f", scale);
        }
        printf("\n______________\n");
        if (scale == 0)
        {
            e[i] = d[i - 1];
            for (int j = 0; j < i; ++j)
            {
                d[j] = V[(i - 1)+j*ldv];
                V[i+j*ldv] = 0;
                V[j+i*ldv] = 0;
            }
        }
        else
        {
            // generate Householder vector
            for (int k = 0; k < i; ++k)
            {
                d[k] /= scale;
                h += d[k] * d[k];
            }

            float f = d[i - 1];
            float g = sqrt(h);
            if (f > 0)
                g = -g;

            e[i] = scale * g;
            h = h - f * g;
            d[i - 1] = f - g;

            for (int j = 0; j < i; ++j)
                e[j] = 0;

            // Apply similarity transformation to remaining columns.
            for (int j = 0; j < i; ++j)
            {
                f = d[j];
                V[j+i*ldv] = f;
                g = e[j] + V[j+j*ldv] * f;

                for (int k = j + 1; k <= i - 1; ++k)
                {
                    g += V[k+j*ldv] * d[k];
                    e[k] += V[k+j*ldv] * f;
                }
                e[j] = g;
            }

            f = 0;
            for (int j = 0; j < i; ++j)
            {
                e[j] /= h;
                f += e[j] * d[j];
            }

            float hh = f / (h + h);
            for (int j = 0; j < i; ++j)
                e[j] -= hh * d[j];

            for (int j = 0; j < i; ++j)
            {
                f = d[j];
                g = e[j];
                for (int k = j; k <= i - 1; ++k)
                    V[k+j*ldv] -= (f * e[k] + g * d[k]);

                d[j] = V[(i - 1)+j*ldv];
                V[i+j*ldv] = 0;
            }
        }
        d[i] = h;
    }

    // accumulate transformations
    for (int i = 0; i < n - 1; i++)
    {
        V[n - 1+i*ldv] = V[i+i * ldv];
        V[i+i * ldv] = 1;
        float h = d[i + 1];

        if (h != 0)
        {
            for (int k = 0; k <= i; ++k)
                d[k] = V[k+(i + 1) *ldv] / h;

            for (int j = 0; j <= i; ++j)
            {
                float g = 0;
                for (int k = 0; k <= i; ++k)
                    g += V[k+(i + 1) * ldv] * V[k+j * ldv];

                for (int k = 0; k <= i; ++k)
                    V[k+j * ldv] -= g * d[k];
            }
        }

        for (int k = 0; k <= i; ++k)
            V[k+(i + 1) * ldv] = 0;
    }

    for (int j = 0; j < n; ++j)
    {
        d[j] = V[(n - 1)+j * ldv];
        V[(n - 1)+j * ldv] = 0;
    }

    V[(n - 1)+(n - 1) * ldv] = 1;
    e[0] = 0;
}

float max(float x, float y) {
    return (x > y) ? x : y;
}

void swap(float& x, float& y) {
    float tmp;
    tmp = x;
    x = y;
    y = tmp;
}

void tql2(float* V, float* d, float* e, int n, int ldv)
{
    for (int i = 1; i < n; ++i)
        e[i - 1] = e[i];
    e[n - 1] = 0;

    float f = 0;
    float tst1 = 0;
    float eps = pow(2.0, -52.0);

    for (int l = 0; l < n; ++l)
    {
        // find small subdiagonal element
        tst1 = max(tst1, fabs(d[l]) + fabs(e[l]));
        int m = l;

        // original while-loop from Java code
        while (m < n)
        {
            if (fabs(e[m]) <= eps * tst1)
                break;
            m++;
        }

        // if m == l, d[l] is an eigenvalue, otherwise, iterate
        if (m > l)
        {
            int iter = 0;
            do
            {
                iter = iter + 1;

                // compute implicit shift
                float g = d[l];
                float p = (d[l + 1] - g) / (2.0 * e[l]);
                float r = hypot(p, 1.0);
                if (p < 0)
                    r = -r;

                d[l] = e[l] / (p + r);
                d[l + 1] = e[l] * (p + r);
                float dl1 = d[l + 1];
                float h = g - d[l];

                for (int i = l + 2; i < n; ++i)
                    d[i] -= h;
                f += h;

                // implicit QL transformation.
                p = d[m];
                float c = 1;
                float c2 = c;
                float c3 = c;
                float el1 = e[l + 1];
                float s = 0;
                float s2 = 0;

                for (int i = m - 1; i >= l; --i)
                {
                    c3 = c2;
                    c2 = c;
                    s2 = s;
                    g = c * e[i];
                    h = c * p;
                    r = hypot(p, e[i]);
                    e[i + 1] = s * r;
                    s = e[i] / r;
                    c = p / r;
                    p = c * d[i] - s * g;
                    d[i + 1] = h + s * (c * g + s * d[i]);

                    // accumulate transformation.
                    for (int k = 0; k < n; ++k)
                    {
                        h = V[k+(i + 1)*ldv];
                        V[k+(i + 1) * ldv] = s * V[k+i * ldv] + c * h;
                        V[k+i * ldv] = c * V[k+i * ldv] - s * h;
                    }
                }

                p = -s * s2 * c3 * el1 * e[l] / dl1;
                e[l] = s * p;
                d[l] = c * p;

            } while (fabs(e[l]) > eps * tst1);
        }

        d[l] += f;
        e[l] = 0;
    }

    // Sort eigenvalues and corresponding vectors.
    for (int i = 0; i < n - 1; ++i)
    {
        int k = i;
        float p = d[i];

        for (int j = i + 1; j < n; ++j)
            if (d[j] < p)
            {
                k = j;
                p = d[j];
            }

        if (k != i)
        {
            d[k] = d[i];
            d[i] = p;
            for (int j = 0; j < n; ++j)
                swap(V[j+i * ldv], V[j+k * ldv]);
        }
    }
}

void eigen_vector_decompose_hermitian(float2* A, int N, int lda, float2* V_cevd, float* d_cevd)
{

    int n = 2 * N;
    int lds = n;
    float* S = nullptr;

    S = (float*)malloc(lds * n * sizeof(float));
    real_neimag_real_imag_fill((float2*)A, N, lda, S, n, lds);
    printf("S(ma)=\n");
    print_matrix(S, n, n, lds);
    //______________________________________________________________

    int ldv_evd = n;
    float* V_evd = nullptr;

    V_evd = (float*)malloc(lds * n * sizeof(float));
    memcpy(V_evd, S, lds * n * sizeof(float));
    printf("V_evd(ma)=\n");
    print_matrix(V_evd, n, n, ldv_evd);

    float* e = nullptr;
    float* d_evd = nullptr;
    e = (float*)malloc(n * sizeof(float));
    d_evd = (float*)malloc(n * sizeof(float));

    //______________________________________________________________
    //void tred2(float* V, float* e, float* d, int n, int ldv);
    tred2(V_evd, d_evd, e, n, ldv_evd);
    printf("V_evd-tred2=\n");
    print_matrix(V_evd, n, n, ldv_evd);
    printf("\nd-tred2=\n");
    print_vector(d_evd, n);
    printf("\ne-tred2=\n");
    print_vector(e, n);


    //void tql2(float* V, float* d, float* e, int n, int ldv);
    tql2(V_evd, d_evd, e, n, ldv_evd);
    printf("\nV_evd-tql2=\n");
    print_matrix(V_evd, n, n, ldv_evd);
    printf("\nd-tql2=\n");
    print_vector(d_evd, n);
    printf("\ne-tql2=\n");
    print_vector(e, n);
    //_________________________________________________________________________________
    /**float* d_cevd = nullptr;
    float2* V_cevd = nullptr;



    d_cevd = (float*)malloc(N * sizeof(float));
    V_cevd = (float2*)malloc(ldv_cevd * N * sizeof(float2));
    */
    int ldv_cevd = N;

    for (int i = 0; i < N; i++)
        d_cevd[i] = d_evd[2 * i];

    printf("\nd_cevd=\n");
    print_vector(d_cevd, N);

    for (int j = 0; j < N; ++j)
    {
        int j2 = 2 * j;
        for (int i = 0; i < N; ++i) {
            V_cevd[i + j * ldv_cevd].x = V_evd[i + j2 * ldv_evd];//complex(RV[i][j2], RV[i + N][j2]);
            V_cevd[i + j * ldv_cevd].y = V_evd[(i + N) + j2 * ldv_evd];
        }
    }
    printf("\nV_cevd=\n");
    print_matrix_complex(V_cevd, N, N, ldv_cevd);



}


void print_vector(float* A, int N) {
    for (int idx = 0; idx < N; idx++) {
        printf("%7.4f ", A[idx]);
    }
}
void print_matrix(float* A, int M, int N, int lda)
{
	for (int i = 0; i < M; i++) {
		for (int j = 0; j < N; j++) {
			printf("%7.4f ", A[i + j * lda]);
		}
		printf("\n");
	}
}
void print_matrix_complex(float2* A, int M, int N, int lda) {
	for (int i = 0; i < M; i++) {
		for (int j = 0; j < N; j++) {//*(sizeof(complex)/sizeof(float))
			printf("(%7.4f, %7.4f)", A[i + j * lda].x, A[i + j * lda].y);
		}
		printf("\n");
	}
}

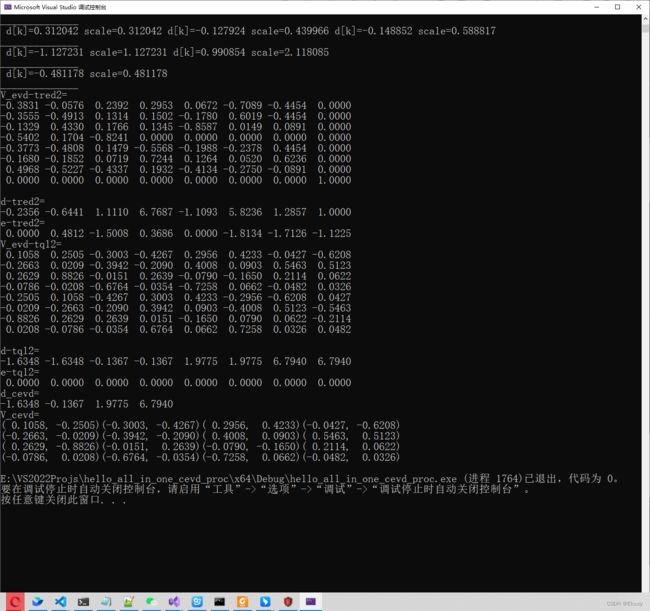
运行：

 

结果分析：

 

matlab: