关联规则算法总结

目的：两个属性是否相关联的研究

物品集I里面是物品，事务集

事务T支持物品集A：这个事务中包含此物品

支持度

物品A的支持度：1000个顾客购物，200个买了面包，支持度20%(200/1000)

关联规则A->B的支持度(联合概率)：1000个顾客购物，100个购买了面包和黄油。则面包->黄油 10%

可信度

关联规则A->B的可信度(条件概率)：1000个顾客购物，200个购买了面包,140个购买了面包和黄油，则可信度为70%(140/200)

A->B的支持度和B->A的支持度一样，可信度不同。

规则度量

最小支持度minsup：关联规则必须满足的最小支持度

最小可信度minconf：关联规则必须满足的最小可信度

大项集

频繁项集：支持度不小于minsup的物品集

最大频繁项目集：频繁集中挑选出所有不被其他元素包含的平凡项目集。

关联规则发现任务

事务数据库D，满足最小支持度和最小可信度的关联规则

1)求D中满足最小支持度的所有频繁集(Apriori算法和FP树都是找频繁集的算法)。大于支持度

2)利用频繁集生成满足最小可信度的所有关联规则。大于可信度

高效求出频繁集：生成长度为1的L[1]；L[k]的基础上生成候选物品集C[k+1],候选物品集必须保证包括所有的频繁项集。

频繁集向下封闭性，频繁集子集必是频繁集；非频繁集的超集必是非频繁集

Apriori算法（生成测试法）——构造候选集->组合频繁集

思想：找单项候选集，去掉小于事先设定最小支持度的项，得单项频繁集；组合为两项候选集，再去掉小于事先设定最小支持度的项，得两项频繁集。以此类推！

注意：组合时及时修剪。k项到k+1项时，可以将它排序，前k-1项都一样,然后将两个集合的第k项加入(此方法选的只多不少，需要再筛选一次)

伪代码：

优化：基于划分方法/Hash/采样/减小交易个数

瓶颈：候选集的生成(1、组成更长频繁集太多。2、最长模式n，则需n+1次扫描数据库)

注意的问题：充分理解数据、目标明确、数据工作做好、最小的支持度和可信度、理解关联规则

使用步骤：连接数据，做数据准备；给定最小支持度和可信度，发现关联规则；可视化与评估

FP-树算法——构造FP-树->挖掘频繁集

原理：

1.两次数据库搜索。一次对所有1-项目进行频度排序，一次将数据库信息转化为紧致内存(即FP-tree)

2.根据FP-tree生成频繁集。为树上每个节点生成条件模型库；用条件模型库构造对应的条件FP树；递归挖掘条件FP树，并增长频繁集。

步骤：

1.找单项集的频次，并将大于等于minsup的项目进行排序，形成项头表。构建一个Null结点的FP树

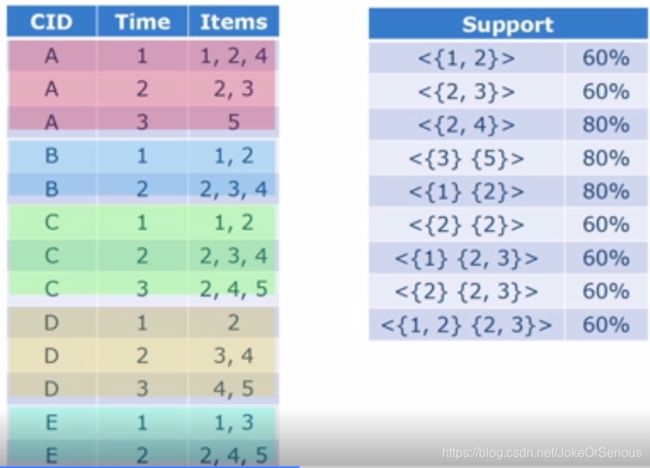
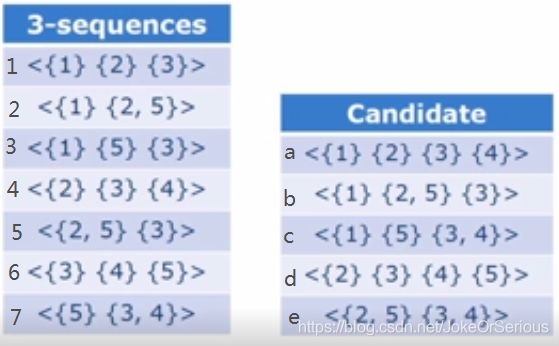
2.将数据库中的每一条记录进行过滤排序(过滤即删去频次

3.将排序后的数据插入FP树中，记录路过一次结点，结点频次加一。

4.不断进行2-3步，直到每一条记录都插入FP树，FP树即构造完成

5.FP-growth，按项头表的逆序(即从下往上)，依次选定结点，并在FPtree中找到能到达该结点的路径(条件模式基)

6.根据条件模式基找到频繁集

具体算法和例子在这篇博客中讲的很清楚https://www.cnblogs.com/pinard/p/6307064.html

缺点：需要递归，所以内存开销大。只适用于单维的布尔关联规则。

 

上面观察的是用户单次购物买这些东西和买另一些东西的关系；

下面观察的是用户的上次购物买的东西和下次购物买的东西的关系。

序列模式(sequential pattern)——交易有先后关系

如图,有五个用户A,B,C,D,E分别有3,2,3,3,2次购买记录,A用户第一次买了物品{1,2,4},第二次买了物品{2,3},第三次买了物品{5}

<{1,2}>代表某用户某次购买时同时买了物品1和2；<{1}{2}>代表某用户某次购买了物品1,之后在另一次购买时又购买了物品2

支持度的分母代表记录几个人，这里就是5。分子代表有几个人买过(不论是哪次购物)

候选集生成

两个长度为k(有k个数，不关注几个大括号)的序列，一个去头，一个去尾，若中间相同，则将两个集合合并

a的生成：1去首{1}==4去尾{4}，则a=1+4

b的生成：2去首{1}==5去尾{3}，则b=2+5

c的生成：3去首{1}==7去尾{3,4}中的4，则c=3+7

d的生成：4去首{2}==6去尾{5}，则d=4+6

e的生成：5去首{2,5}中的2==7去尾{3,4}中的4，则e=5+7

上面生成的之多不少，再进行pruning最终只有b.