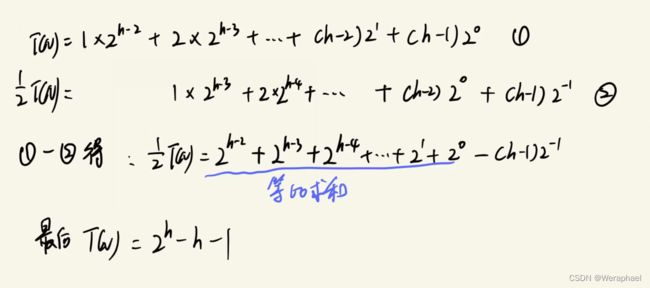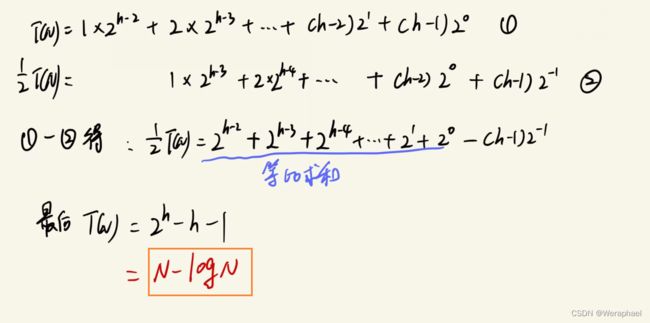【数据结构】堆的应用（堆排序的实现 + （向上/向下）建堆时间复杂度证明 + TopK问题（笔记总结））

个人主页：@Weraphael
✍作者简介：目前学习C++和算法
✈️专栏：数据结构
希望大家多多支持，咱一起进步！
如果文章对你有帮助的话
欢迎 评论 点赞 收藏 加关注✨

---

【本章内容】

一、堆排序

1.1 堆排序的思想

堆排序即利用堆的思想来进行排序，总共分为两个步骤：

1. 建堆
   升序：建大堆
   降序：建小堆
2. 利用堆删除思想来进行排序
   建堆和堆删除中都运用到了向下调整。但是，建堆也可以用向上调整，只是向上调整的时间复杂度高于向下调整（后面有证明过程）

1.2 堆排序排升序思路

在《堆排序的思想》中，总结了升序要建大堆，为什么要建大堆呢？首先大堆的特点是：父亲结点总大于或等于孩子结点。因此建完大堆后，根节点就是最大的，而又要保持升序。所以，我们可以将根结点和尾结点进行交换，这样最大的元素就在最后一个了，然后再以根结点向下调整（注意调整的时候不要再动尾结点了），这样次大的元素又在根结点上了，重复以上操作，即可以用堆排序排升序。

1.3 建堆

1.31 向上调整建堆

• 向上调整建堆就是从第二层模拟插入的过程

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void AdjustUp(int* a, int child)
{
	//找到父亲节点
	int parent = (child - 1) / 2;

	while (child > 0) 
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			//迭代
			child = parent;
			parent = (child - 1) / 2;
		}
		//如果尾插的节点不比其父亲大，就没必要比了
		else
		{
			break;
		}
	}
}

void HeapSort(int* a, int n)
{
	//1. 建堆
	//法一：向上调整建堆(大堆)
	for (int i = 1; i < n; i++)
	{
		Adjust(a, i);
	}
}

int main()
{
	int a[] = { 4,7,10,8,1,5,2,3 };
	
	//数组元素个数Asize
	int Asize = sizeof(a) / sizeof(a[0]); 

	//堆排序
	HeapSort(a, Asize);
	
	//打印
	for (int i = 0; i < Asize; i++)
		printf("%d ", a[i]);

	printf("\n");

	return 0;
}

此篇博客详细讲解了建大堆的过程 -->【传送门】

1.32 向上建堆时间复杂度证明

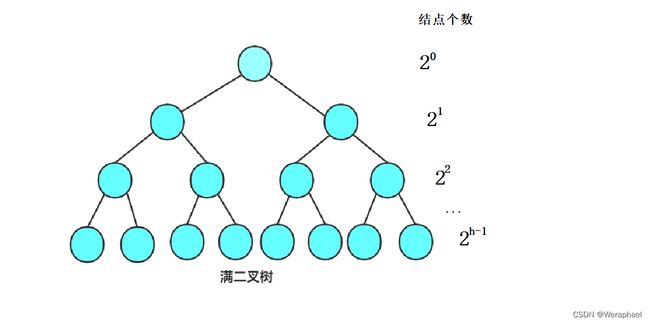
由于一般时间复杂度通常都是看最坏的，因此以满二叉树为例，因为它的结点个数最多。

向上建堆是从第二层开始模拟插入过程的。现假设二叉树的高度为h,T(N)表示建堆的总次数。那如何列出总次数的式子呢？我们可以拿（每一层结点个数如上图）每一层结点的个数 × 最坏调整次数。例如，从第二层开始向上建堆可以列出 $2^1\times 1$，第三层可以列出 $2^2\times 2$。后面因此类推。所以可以列出以下T(N)的表达式：
$$T(N)=2^1\times 1+2^2\times 2+2^3\times 3+...+2^{(}h-2)\times (h-2)+2^{(}h-1)\times (h-1)$$
那该如何化简呢？这就要运用到高中的数学知识 — 错位相减法

再通过以下结论：
设满二叉树高度为h，总结点个数为N

• 满二叉树的总结点个数 ： $N=2^h-1$
• 再根据数学知识化简以上等式：$h=logN$ (以2为底）

带入结论得出：向上建堆的时间复杂度为：NlogN

1.33 向下调整建堆

#include 
//堆排序

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void AdjustDown(int* a, int n, int parent)
{
	//假设左孩子一开始最大
	int child = parent * 2 + 1;
	//当child走到叶子节点循环结束，也就是说它不能超过数组的大小
	while (child < n)
	{
		//判断右孩子是否真的比左孩子大
		//注意还要防止数组越界
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}

		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			//迭代
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* a, int n)
{
	//1. 建堆
	//法二：向下调整建堆(大堆)
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		Adjustdown(a, n, i);
	}
// i - 开始向下调整的根的下标
// n - 需要调整的元素个数
}

这里需要注意的是，这里的向下调整并不是从根结点开始的，而是从倒数第一个非叶子结点开始的。为什么呢？因为一开始数组内的元素都是随机的，而向下调整必须要满足左右子树都要有堆的性质。画个图可能会更加清晰点：

然后再来解释向下调整循环的细节，前头说过了，要从倒数第一个非叶子结点开始向下调整，对于上图来说，非叶结点的第一个结点也就是15，那么问题来了，如何找到15呢，在堆的章节已经说过了父亲结点和孩子结点的下标关系了

1. 如何找到父亲结点：parent = （child - 1）/ 2
2. 如何找到左孩子结点 ：leftchild = parent * 2 + 1
3. 如何找到右孩子结点：rightchild = parent * 2 + 2（右孩子比左孩子的下标多1）

所以可以通过500的下标找到15，因此循环里的(n - 1 - 1) / 2的n - 1代表的是最后一个元素的下标，再-1 /2即找到倒数第一个非叶子结点。

1.34 向下建堆时间复杂度证明

和向上建堆的时间复杂度一样，以满二叉树为例

在向下调整过程中，由于是从倒数第二层结点开始向下调整的，倒数第二层结点总个数不难算出是 2^(h-2)。现假设二叉树的高度为h,T(N)表示建堆的总次数。通过每一层结点的个数 × 最坏调整次数列出T(n)表达式如下：
$$T(N)=2^{(}h-2)\times 1+2^{(}h-3)\times 2+...+2^1\times (h-2)+2^0\times (h-1)$$
然后通过错位相减法，过程如下：

再通过以下结论：
设满二叉树高度为h，总结点个数为N

• 满二叉树的总结点个数 ： $N=2^h-1$
• 再根据数学知识化简以上等式：$h=logN$ (以2为底）

带入结论得出：向下建堆的时间复杂度为：O(N)

总结：
向上建堆的时间复杂度为：O(NlogN)，向下建堆的时间复杂度为：O(N)。因此，建堆时一般都使用向上建堆。

1.4 调整

我们已经完成了建堆，接下来根据《堆排序排升序思路》。将根结点和尾结点进行交换，然后再以根结点向下调整（注意调整的时候不要再动尾结点了），这样次大的元素又在根结点上了，重复以上操作，即可以用堆排序排升序。

1.41 调整代码实现

#include 
//堆排序

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void AdjustDown(int* a, int n, int parent)
{
	//假设左孩子一开始最大
	int child = parent * 2 + 1;
	//当child走到叶子节点循环结束，也就是说它不能超过数组的大小
	while (child < n)
	{
		//判断右孩子是否真的比左孩子大
		//注意还要防止数组越界
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}

		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			//迭代
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}


void HeapSort(int* a, int n)
{
	//1. 建堆
	//法二：向下调整建堆(大堆)
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	//2. 调整
	int end = n - 1;//最后一个元素
	while (end > 0)
	{
		//首尾交换
		Swap(&a[0], &a[end]);
		//向下调整
		AdjustDown(a, end, 0);
		end--;
	}
	//end是最后一个元素的下标
	//同时也是前面数据的个数
}

注意
交换完头尾两个元素后，向下调整的区间不要包括最后一个元素，因为最后一个元素已经是当前所有元素中最大的了

1.42 调整复杂度证明

可以这么想，因为满二叉树最后一层的结点个数占总结点个数的一半，因此可以只看最后一层
$$T(N)=2^{(}h-1)\times (h-1)=NlogN$$

1.5 完整代码 + 整体时间复杂度

//堆排序
#include 

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void AdjustDown(int* a, int n, int parent)
{
	//假设左孩子一开始最大
	int child = parent * 2 + 1;
	//当child走到叶子节点循环结束，也就是说它不能超过数组的大小
	while (child < n)
	{
		//判断右孩子是否真的比左孩子大
		//注意还要防止数组越界
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}

		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			//迭代
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* a, int n)
{
	//1. 建堆
	//法二：向下调整建堆(大堆)
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	//2. 调整
	
	int end = n - 1;//最后一个元素
	while (end > 0)
	{
		//首尾交换
		Swap(&a[0], &a[end]);
		//向下调整
		AdjustDown(a, end, 0);
		end--;
	}
}

int main()
{
	int a[] = { 4,7,10,8,1,5,2,3 };
	
	//数组元素个数Asize
	int Asize = sizeof(a) / sizeof(a[0]); 

	//堆排序
	HeapSort(a, Asize);
	
	//打印
	for (int i = 0; i < Asize; i++)
		printf("%d ", a[i]);

	printf("\n");

	return 0;
}

【结果展示】

.总结
向上建堆的时间复杂度是O(N)，调整的时间复杂度是O(NlogN)。因此，堆排序的时间复杂度为O(Nlog(N)

二、TOP-K问题

2.1 什么是TOP-K问题

• TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
• TOP-K在生活中的应用：在班级取成绩前10名、游戏中给段位高的前100的玩家排名等。

2.2 TOP-K问题的基本思路

对于Top-K问题，能想到的最简单直接的方式就是排序。但是，如果数据量非常大，排序就不太可取了(因为数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决。基本思路如下：

1. 用数据集合中前K个元素来建堆

• 取前k个最大的元素，则建小堆
• 取前k个最小的元素，则建大堆

2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

2.3 取最大的前TOP-K

假设我们要取最大的前k个（取最小的前k个也是如此），就要建小堆，然后随机放入K个数据。为什么呢？因为小堆的特点是根结点是整个数据中最小的，然后剩余的N - K个元素依次与堆顶元素来比较，如果大于堆顶元素则交换，然后再进行向下调整。最后，重复以上操作，堆中小的数据都已经被替换了，剩下的就是最大的前K个

2.4 代码实现

• 建小堆

#include 
#include 

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void AdjustDown(int* a, int n, int parent)
{
	//假设左孩子一开始最大
	int child = parent * 2 + 1;
	//当child走到叶子节点循环结束，也就是说它不能超过数组的大小
	while (child < n)
	{
		//判断右孩子是否真的比左孩子大
		//注意还要防止数组越界
		if (child + 1 < n && a[child + 1] < a[child])
		{
			child++;
		}
		//小堆
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			//迭代
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void GetTopK(int* a, int n, int k)
{
	//1. 建堆
	int* SmallHeap = (int*)malloc(sizeof(int) * k);
	if (SmallHeap == NULL)
		return;
	//2. 随机放入k个数据
	for (int i = 0; i < k; i++)
	{
		SmallHeap[i] = a[i];
	}
	//3. 建小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(SmallHeap, k, i);
	}
}

• 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

//4. 将剩下的n - k个元素依次和堆顶元素比较
	for (int i = k; i < n; i++)
	{
		//如果n-k个元素中有大于堆顶则交换
		if (a[i] > SmallHeap[0])
		{
			SmallHeap[0] = a[i];
			//交换完后再调整堆
			AdjustDown(SmallHeap, k, 0);
		}
	 }
	//5.打印
	for (int i = 0; i < k; i++)
	{
		printf("%d ", SmallHeap[i]);
	}
	printf("\n");

【完整代码】

// TopK问题：以找出N个数里面最大为例

#include 
#include 
#include 
void Swap(int* a1, int* a2)
{
	int tmp = *a1;
	*a1 = *a2;
	*a2 = tmp;
}

//小堆：父亲比孩子小
void AdjustDown(int* a, int n, int parent)
{
	//child一开始最小
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] < a[child])
		{
			child++;
		}
		//小堆
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void PrintTopK(int* a, int n, int k)
{
	//1.建堆
	int* SmallHeap = (int*)malloc(sizeof(int) * k);
	assert(SmallHeap);
	//2. 随机向堆丢入k个数据
	for (int i = 0; i < k; i++)
	{
		SmallHeap[i] = a[i];
	}

	//3.建小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(SmallHeap, k, i);
	}

	//4. 将剩下的n - k个元素依次和堆顶元素比较
	for (int i = k; i < n; i++)
	{
		//如果n-k个元素中有大于堆顶则交换
		if (a[i] > SmallHeap[0])
		{
			SmallHeap[0] = a[i];
			//交换完后再调整堆
			AdjustDown(SmallHeap, k, 0);
		}
	}
	//5.打印
	for (int i = 0; i < k; i++)
	{
		printf("%d ", SmallHeap[i]);
	}
	printf("\n");
}

int main()
{
	int a[] = { 20, 100, 4, 2, 87, 9, 8, 5, 46, 26 };
	int k = 3;
	int n = sizeof(a) / sizeof(a[0]);

	PrintTopK(a, n, k);
	return 0;
}