滑模控制学习笔记(三)
滑模控制学习笔记(三)
- 基于趋近律的滑模控制
-
- 几种典型的趋近律
-
- 等速趋近律
- 指数趋近律
- 幂次趋近律
- 一般趋近律
- 基于趋近律的控制器设计
-
- 仿真实例
-
- 状态空间模型建立
- 滑模控制器模型建立
- 仿真结果
- 基于趋近律的滑模鲁棒控制
-
- 仿真实例
基于趋近律的滑模控制
滑模运动包括趋近运动和滑模运动两个过程。系统从任意状态趋近于滑模面,直到到达切换面的运动称为趋近运动,即 s → 0 s\rarr0 s→0的过程。根据滑模变结构原理,滑模可达性条件仅保证由状态空间任意运动点在有限时间内到达切换面的要求,而对于趋近运动具体轨迹未作任何限制,采用趋近律的方法可以改善趋近运动的动态品质。
几种典型的趋近律
等速趋近律
s ˙ = − ϵ s i g n ( s ) ϵ > 0 (1) \dot s = -\epsilon sign(s) \ \ \ \epsilon>0 \tag1 s˙=−ϵsign(s) ϵ>0(1)特点: ϵ \epsilon ϵ越小,趋近速度慢; ϵ \epsilon ϵ越大,引起的抖动越大。
指数趋近律
s ˙ = − ϵ s i g n ( s ) − k s ϵ > 0 , k > 0 (2) \dot s = -\epsilon sign(s) -ks\ \ \ \epsilon >0,\ k>0 \tag2 s˙=−ϵsign(s)−ks ϵ>0, k>0(2)特点:指数项 − k s -ks −ks能保证当 s s s较大时,系统能以较大的速度趋近滑动模态。因此,指数趋近律尤其适合解决具有大阶跃的响应控制问题。
注:指数趋近律中,为了保证快速趋近的同时削弱抖振,应在增大 k k k的同时减小 ϵ \epsilon ϵ。
幂次趋近律
s ˙ = − k ∣ s ∣ α s i g n ( s ) k > 0 , 1 > α > 0 (3) \dot s = -k|s|^\alpha sign(s)\ \ \ k>0,\ 1>\alpha >0 \tag3 s˙=−k∣s∣αsign(s) k>0, 1>α>0(3)特点:通过调整 α \alpha α可保证系统状态远离滑模面时以较大的速度趋近于滑动模态;系统状态趋近滑模面时以较小的速度趋近于滑动模态,以降低抖振。
一般趋近律
s ˙ = − ϵ s i g n ( s ) − f ( s ) ϵ > 0 (4) \dot s = -\epsilon sign(s) - f(s)\ \ \ \epsilon >0 \tag4 s˙=−ϵsign(s)−f(s) ϵ>0(4)其中, f ( 0 ) = 0 f(0)=0 f(0)=0,当 s ≠ 0 s\neq0 s=0时, s f ( s ) > 0 sf(s)>0 sf(s)>0。
基于趋近律的控制器设计
考虑如下被控对象: θ ¨ = − f ( θ , t ) + b u ( t ) (5) \ddot \theta = -f(\theta,t)+b\ u(t) \tag5 θ¨=−f(θ,t)+b u(t)(5)其中, f ( θ , t ) f(\theta ,t) f(θ,t)和 b b b为已知且 b > 0 b>0 b>0。
滑模函数为: s ( t ) = c e ( t ) + e ˙ ( t ) c > 0 (6) s(t) = ce(t)+\dot e(t)\ \ c>0\tag6 s(t)=ce(t)+e˙(t) c>0(6)
跟踪误差为: e ( t ) = θ d ( t ) − θ ( t ) , e ˙ ( t ) = θ ˙ d ( t ) − θ ˙ ( t ) (7) e(t) = \theta_d (t) - \theta (t),\ \ \dot e(t) = \dot \theta_d (t) - \dot \theta (t)\tag7 e(t)=θd(t)−θ(t), e˙(t)=θ˙d(t)−θ˙(t)(7)其中, θ d \theta_d θd为理想位置信号。
设采用指数趋近律,则需要满足 s ˙ = − ϵ s i g n ( s ) − k s ϵ > 0 , k > 0 (8) \dot s = -\epsilon sign(s) - ks\ \ \epsilon>0,k>0\tag8 s˙=−ϵsign(s)−ks ϵ>0,k>0(8)
根据滑模函数可得: s ˙ = c e ˙ + e ¨ = c ( θ ˙ d − θ ˙ ) + ( θ ¨ d − θ ¨ ) = c ( θ ˙ d − θ ˙ ) + ( θ ¨ d + f ( θ , t ) − b u ( t ) ) (9) \dot s = c\dot e+\ddot e = c(\dot \theta_d -\dot \theta)+(\ddot \theta_d -\ddot \theta) = c(\dot \theta_d -\dot \theta)+(\ddot \theta_d +f(\theta,t)-bu(t))\tag9 s˙=ce˙+e¨=c(θ˙d−θ˙)+(θ¨d−θ¨)=c(θ˙d−θ˙)+(θ¨d+f(θ,t)−bu(t))(9)综合式(8)(9),可得到: c ( θ ˙ d − θ ˙ ) + ( θ ¨ d + f ( θ , t ) − b u ( t ) ) = − ϵ s i g n ( s ) − k s (10) c(\dot \theta_d -\dot \theta)+(\ddot \theta_d +f(\theta,t)-bu(t)) =-\epsilon sign(s) - ks\tag{10} c(θ˙d−θ˙)+(θ¨d+f(θ,t)−bu(t))=−ϵsign(s)−ks(10)整理得指数趋近律对应控制律为: u ( t ) = 1 b ( ϵ s i g n ( s ) + k s + c ( θ ˙ d − θ ˙ ) + θ ¨ d + f ( θ , t ) ) (11) u(t) = \frac{1}{b}(\epsilon sign(s)+ks+c(\dot \theta_d -\dot \theta)+\ddot \theta_d +f(\theta,t))\tag{11} u(t)=b1(ϵsign(s)+ks+c(θ˙d−θ˙)+θ¨d+f(θ,t))(11)
仿真实例
考虑被控对象如下: θ ¨ ( t ) = − 25 θ ˙ ( t ) + 133 u ( t ) (12) \ddot \theta (t) = -25\dot\theta(t) +\ 133u(t) \tag{12} θ¨(t)=−25θ˙(t)+ 133u(t)(12)
状态空间模型建立
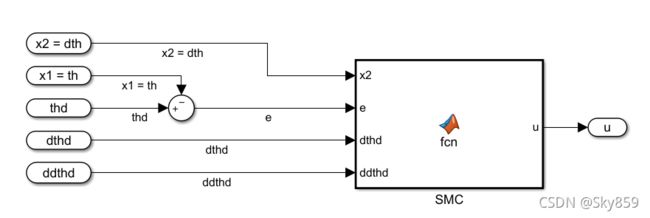
滑模控制器模型建立
根据式(11),取 K = 10 , C = 15 , ϵ = 5 K = 10,C= 15,\epsilon = 5 K=10,C=15,ϵ=5,建立指数趋近律滑模控制器如下:
function u = fcn(x2,e,dthd,ddthd)
K = 10;
C = 15;
eps = 5;
dth = x2;
de = dthd - dth;
s = C*e + de;
u = (eps*sign(s) + K*s + C*de+ ddthd + 25*dth)/133;
end
仿真结果
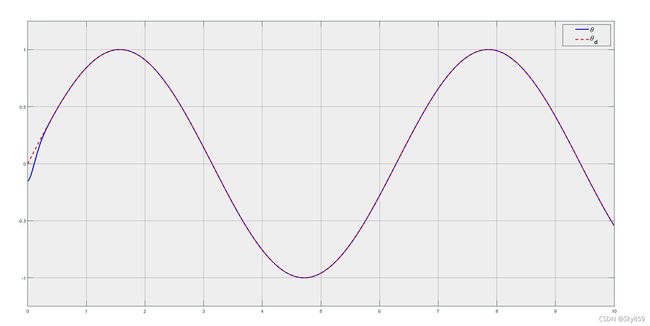
取位置函数为 θ d = s i n t \theta_d = sint θd=sint,则 θ ˙ d = c o s t , θ ¨ d = − s i n t \dot \theta_d = cost,\ddot \theta_d = -sint θ˙d=cost,θ¨d=−sint,设初始状态 [ x 1 x 2 ] = [ − 0.15 − 0.15 ] [x_1\ \ x_2] = [-0.15 \ -0.15] [x1 x2]=[−0.15 −0.15]仿真结果如下:
分别取 k = 0 , k = 5 , k = 10 k=0,k=5,k=10 k=0,k=5,k=10,并将 e e e和 e ˙ \dot e e˙输出至workspace绘制相轨迹:

可以看到,通过增大k可以更快的趋近于滑模面,但抖振的问题仍然存在。
基于趋近律的滑模鲁棒控制
考虑被控对象与上例相同,但收到扰动 d ( t ) d(t) d(t),则运动方程如下: θ ¨ ( t ) = − f ( θ , t ) + b u ( t ) + d ( t ) (13) \ddot \theta(t) = -f(\theta,t)+bu(t)+d(t) \tag{13} θ¨(t)=−f(θ,t)+bu(t)+d(t)(13)采用与上例相同的滑模函数,且选择指数趋近律,得到如下方程: c ( θ ˙ d − θ ˙ ) + ( θ ¨ d + f − b u − d ) = ϵ s i g n ( s ) − k s (14) c(\dot \theta_d - \dot \theta )+(\ddot \theta _d +f-bu-d) = \epsilon sign(s) -ks \tag{14} c(θ˙d−θ˙)+(θ¨d+f−bu−d)=ϵsign(s)−ks(14)则控制律为: u ( t ) = 1 b ( ϵ s i g n ( s ) + k s + c e ˙ + θ ¨ d + f − d ) (15) u(t) = \frac{1}{b}(\epsilon sign(s)+ks+c\dot e+\ddot \theta_d+f-d) \tag{15} u(t)=b1(ϵsign(s)+ks+ce˙+θ¨d+f−d)(15)但由于扰动项 d ( t ) d(t) d(t)为未知项,因此需要其上下界进行控制律设计。
设 d L ≤ d ( t ) ≤ d U d_L\leq d(t)\leq d_U dL≤d(t)≤dU,令 u ( t ) = 1 b ( ϵ s i g n ( s ) + k s + c e ˙ + θ ¨ d + f − d c ) (16) u(t) = \frac{1}{b}(\epsilon sign(s)+ks+c\dot e+\ddot \theta_d+f-d_c) \tag{16} u(t)=b1(ϵsign(s)+ks+ce˙+θ¨d+f−dc)(16)则此时 s ˙ = − ϵ s i g n ( s ) − k s + d c − d (17) \dot s = -\epsilon sign(s) -ks +d_c -d \tag{17} s˙=−ϵsign(s)−ks+dc−d(17)为满足李雅普诺夫稳定条件 s s ˙ = − ϵ ∣ s ∣ − k s 2 + ( d c − d ) s < 0 s\dot s= -\epsilon|s| -ks^2 +(d_c -d)s<0 ss˙=−ϵ∣s∣−ks2+(dc−d)s<0:
(1)若 s > 0 s>0 s>0,可取 d c = d L d_c = d_L dc=dL;
(2)若 s < 0 s<0 s<0,可取 d c = d U d_c = d_U dc=dU;
根据上述两个条件可以得到: d c = d U + d L 2 − d U − d L 2 s i g n ( s ) (18) d_c = \frac{d_U+d_L}{2}-\frac{d_U-d_L}{2}sign(s) \tag{18} dc=2dU+dL−2dU−dLsign(s)(18)
仿真实例
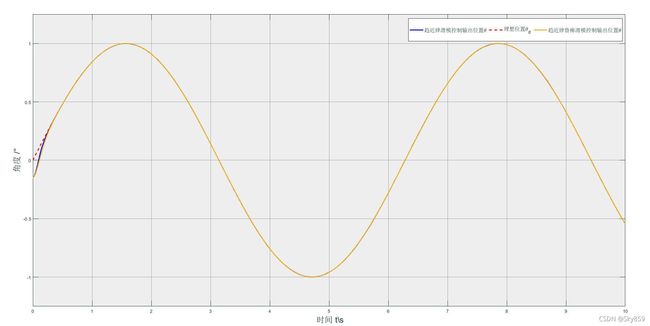
对上例的输入添加扰动 d ( t ) = 10 s i n ( π t ) d(t) = 10sin(\pi t) d(t)=10sin(πt),则 d L = − 10 , d U = 10 , d c = 10 s i g n ( s ) d_L = -10,d_U = 10,d_c =10sign(s) dL=−10,dU=10,dc=10sign(s),构建滑模鲁棒控制 u ( t ) = 1 133 ( ϵ s i g n ( s ) + k s + c e ˙ + θ ¨ d + 25 θ ˙ − d c ) u(t) = \frac{1}{133}(\epsilon sign(s)+ks+c\dot e+\ddot \theta_d +25\dot \theta - d_c) u(t)=1331(ϵsign(s)+ks+ce˙+θ¨d+25θ˙−dc),对比有无鲁棒项的控制律及角度跟踪情况。
function [u,de] = fcn(x2,e,dthd,ddthd)
K = 10;
C = 15;
eps = 5;
du = 10;
dl = -10;
dth = x2;
de = dthd - dth;
s = C*e + de;
d1 = (du-dl)/2;
d2 = (du+dl)/2;
dc = d2-d1*sign(s);
u = (eps*sign(s) + K*s + C*de+ ddthd + 25*dth -dc )/133;
end