Flash 与分布学构想:正弦分布
在之前讲过一些,分布学构想建立对图形位置分布一种概念想法。我们则重点是讲图形放在位置和角度方面上去体现这种构想。它的基点在于位置变化而产生的图像变化。 而今天在矩阵变化基础上,也引入一种正弦分布。这种分布基础是体现在正弦曲线上。
我们知道y=sinx 是最简单的正弦曲线。我们借助他的一些数学知识让我们图形进行一次正弦分布。
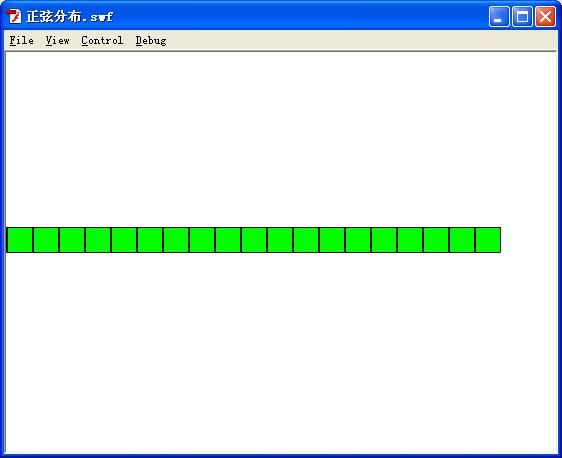
首先我们会建立起一种线性分布。以下图就是一种简单的线性分布矩形排序成的图像就成为线性的情况。姑且成为线性分布。
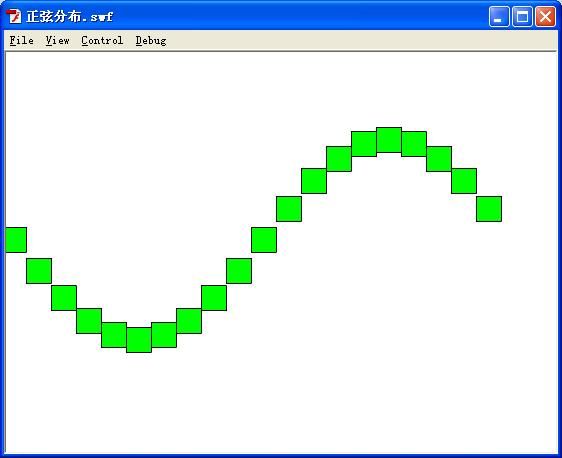
在它基础上,加以变化,将其产生不同位置变化。图形就会向我们所希望的情况出现。
同样加以角度关系变化,我们可以将图形分布呈现另一种情况。
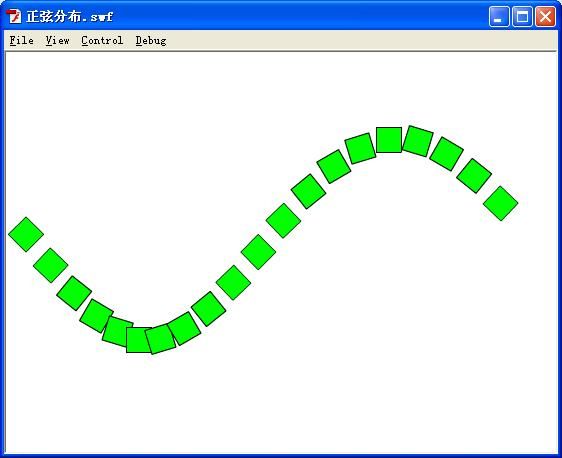
三种图变化情况不一样,但是体现基本思想就是改变他们位置关系,向我们所想的方向设想。它的出发点基于位置变化产生的变化。看起来效果就不一样了。
根据编程的情况,我会先设计第一种线性分布的情况。把目光设定在这里
mc.x=i*mc.width;
mc.y=200;
当他所复制出来的图案,y的位置是不变的,而x位置是发生变化。这种就是最基本线性分布。
其次,当我们想进行正弦分布的时候,显然将mc 的x和y坐标更改即可以实现到。
mc.x=20+i*perAngle/360*500;
mc.y=200+100*Math.sin(perAngle*i*Math.PI/180);
我们借用的是sin 的公式,振幅为100。角度的递增,位置也发生相应改变。其中500是一个任意是数字,有兴趣可以尝试。这种是一个比较有趣的地方。
最后我将一下代码写在下面。里面包含三种情况,可以尝试一下这几种情况。