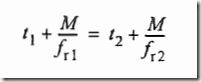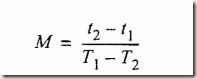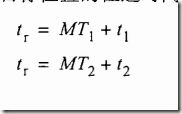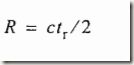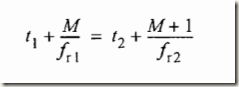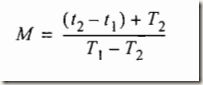距离模糊与多普勒模糊
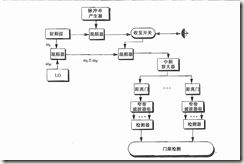
在PD雷达中,发射波形是脉冲调制信号。脉冲雷达的结构如下:
这种波形就产生了两个问题:1 距离模糊 。2多普勒模糊。二者之间又是互相矛盾的,要想有一个大的非模糊距离,则要求PRF低,如果要求减小多普勒模糊,PRF要足够高。
一、距离模糊
雷达进行距离测量,是取得发射信号和回波的时延δt,R=cXδt/2。当回波在下一次发射脉冲之后到达,无法判断回波信号的时延,则会产生距离模糊。
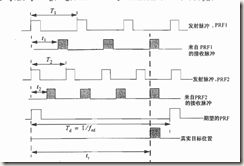
解决办法是最大非模糊距离得出 maximum δt,=Td, 计算frd>=1/ Td. 取 n1,n2=n1+1,则二者质。使1fr1=n1xfrd, fr2=n2Xfrd。在一个T周期内只有一次fr1和fr2的回波时刻重合,如下图所示。
假设M1是发射脉冲与真实目标接收回波之间的PRF1的间隔,M2对应于PRF2。在0到Td内,可能的结果只有M1=M2=M,或M1+1=M2
fr1<fr2 ---> T1>T2
当t1=t2时,真实目标距离为模糊的。
二 多普勒模糊
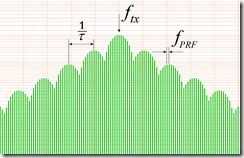
一个周期脉冲调制的信号频谱如下。中心频率为载波频率, 谱线间隔为重频,第一零点是脉宽的倒数。
多普勒频偏小于重频时,可以用来测量非模糊速度。
例如:
多普勒频率fd=2v/λ=33KHz
n1Xfr1+fd1=n1Xfr1+fd1=n1Xfr1+fd1=33
假设n1=0 ,fd1=33>fr1,不成立;n1=1时,fd1=18>fr1, 仍不成立;n1=2时,fd1=3KHz;
同样n2=1时,fd2=15KHz; n3=1时,fd3=12KHz.
对于第二个问题 fd=n1Xfr1+8=n2Xfr2+2=n3Xfr3+17
当n1=n2=2,n3=1时,fd=38KHz