A Translation for Quaternion 一篇对四元数的翻译

 

a. 这是一篇讲解四元数原理的论文翻译，原文参见 这里。

b. 在此之前在网络上找过很多资料，但基本都是结论性的介绍，并未对”为什么“进行深入全面的解释。因此在看完本文并消化理解了以后，我决定将其翻译出来，一方面作为知识总结，一方面为相似境遇的朋友提供帮助。

c. 但并不是说这篇翻译就没什么错误。尤其是在介绍四元数历史的那节，由于缺少必要的数学涵养，我不自信是否翻得正确，还请各位朋友帮忙校准。另外由于英文水准有限，许多地方翻得比较生硬，望请诸位海涵。

d. 文中( 注: ... ) 的部分，是我根据上下文自己进行的推理，不代表作者观点（实际上作者在那些地方什么都没有说，有时候你得自己推一推才能弄明白）。

e. 由于精力和时间关系，我没有翻译全文，只是节选了重要的章节。但相信已经覆盖了必要的四元数的知识，足以支持你完成一个相机系统(Camera System)

f. 之所以说”足以“，是因为我已经用这些理论写完了一个以四元数为支撑的相机。

g. 从开始有想法对它一探究竟，到一步步实现功能，再到总结性地翻译本文，每晚见缝插针挤出约2小时，总共历时近三个月完成。时间之久，身心俱疲。Snake is Old...

 

-------------------------------------------

 

 

四元数

Ken Shoemake
Department of Computer and Information Science
University of Pennsylvania
Philadelphia, PA 19104

 

概要

凡是图形学所涉及到的数学知识，大多数都有详尽完备的介绍，但四元数却是一个例外。本文因此而写。这篇教程介绍了诸如“什么是四元数”、“为何它如此有用”、“怎么用、用在哪里”，以及“使用时机”等话题。

 

 

介绍

在图形学领域，四元数一般用来表达旋转和朝向的概念。在1985年的SIGGRAPH会议上，四元数曲线(quaternion curve) 方法第一次被引入到图形学中，意图使旋转动画(rotation animation)计算变得更加方便。虽然这只是一个相当特殊的案例，但由于四元数出色的表现，令它无论与主流的矩阵表示法相比，还是与小众的欧拉角（Euler angles）表示法相比，都不输分毫。 

 

四元数由此声名大噪，开始作为一种新技术被应用到曲线方法以及众多领域中，如基于物理的建模技术，约束系统（constraint system）以及用户界面（user interface）上。四元数之所以能被广泛应用，是因为就实现而言，与其他同类技术相比，它不仅更加简洁，成本更低，而且更加优雅。不过，研究者和开发者想要掌握它，必须要学习一些新的数学知识，但一般的数学课或者科学课程却都不教授四元数。总之不管怎么说，无论是站在齐次坐标（homogeneous coordinates）的角度看，还是从一个更宽泛的角度看，四元数都不单单是我们所熟知的四维齐次坐标（four-component homogeneous coordinates）的复杂升级版本。

 

 

四元数定义

四元数有好几种定义的方式，这些方式的形态也许有所不同，但实质却彼此等价。了解这些形态是必要的，因为每一种形态对我们都非常有用。历史上， Hamilton首次将四元数定义为形如广义复数的形式： w+ix+jy+kz ， 其中，i² = j² = k² = -1, ij = k = -ji ，并且，i,j,k为虚数，而w,x,y,z为实数，（数学家为了纪念Hamilton，用H表示四元数）。四元数的运算中有一个非常特例：乘法的不可交换性。其余的运算性质则与实数的大同小异。Hamilton就曾意识到可以用这种“相似性”来抽象四元数的特性，具体说就是将四元数简单地看作一个由四个实数组成的集合[x, y, z, w]，并适当地为其定义加法和乘法。然而适逢当时复数的出现，Hamilton就将(x,y,z)“打包”成虚部（Imaginary part），并以术语“向量”（vector）称之，而实数部分(Real part)他就称为“标量”（scalar）。随后的研究者们（主要是Gibbs）直接借用了Hamilton发明的这些术语，并从四元数那脏兮兮、但却很常规的运算法则中提炼出一套更“干净”的法则（extracted from the clean operations of quaternion arithmetic the somewhat messierÑbut more generalÑoperations of vector arithmetic）：即现在的教学课程里都会教授的点积(dot products)与叉积(cross products)运算。对今天的我们而言，我们可以很容易逆观历史，用现代的点积、叉积等概念来描述当时的四元数。

基于以上观点，我们现在来给出一些事实：首先我们一般会这样定义四元数：[v, w]， 其中v是一个向量且等于（x, y, z),  而w是一个实数。假设一个实数s， 如果用四元数形式描述的话，它就等于[0, s]，而一个纯向量v，如果用四元数描述的话，则是[v,0]。 接下来我们给出四元数的一些基本运算法则：

 

  

注意 N(q)是一个标量，所以q的倒数定义很清晰（so the description of q-1 is well-defined）。另外，乘法的不可交换性导致了一些运算需要换用更加清晰的形式来表达（ Otherwise, the non-commutativity of multiplication requires explicit expressions），例如要用 pq^-1 来代替  p/q。
 
上面列出的运算公式中，即有运算本身的定义，也有由定义推导得出的结论。试着将这些结论当作定理推导一番是很有用的，而且不难：每一个证明应该都可以直截了当地计算出来。

  

 

用四元数表示旋转

四元数和三维空间内的旋转关系可以用定理1进行阐述。

定理1：令p为三维（投影）空间内的一个点，用齐次坐标将其表示成四元数的形式即为： p = (x:y:z:w) = [(x, y, z), w] = [v, w] ； 令q为任一非零四元数。那么：

• 结论1)  表达式 qpq^-1的结果将使p=[v, w]变换到p`=[v`, w]， 二者模长相等。
• 结论2)  任何非零实数与q相乘，上式仍然成立。
• 结论3)  如果上式中的q为N(q) = 1（即q为单位四元数），那么q = [ v sinΩ , cos Ω ] 表示一个旋转动作：将p沿着单位轴v 旋转2Ω即得到p'。 

 

证明：让我们先从结论2入手。这个结论很容易证明。由于sq的倒数是q^-1s^-1, 且注意标量的乘法满足交换律，所以我们可以得到：

(sq)·p·(sq)^-1 = sq·p·q^-1s^-1 = qpq^-1ss^-1 = qpq^-1 

 

根据这条结论，我们就可以把这个q直接当作一个单位四元数来看，正如 结论3里所需要的那样，而又不失一般性。对于单位四元数q, 由于q^-1 = q^* ，所以我们可以将 qpq^-1写作 qpq^*。

 

现在来证明结论1就简单多了。一般来说，对一个标量进行一些变换，其结果往往仍是一个标量；类似地，对一个向量[v, 0]进行一系列变换，其结果仍是一个向量。对于任何一个四元数q，其标量部分(即实部) S(q) 可以用公式2S(q) = q + q^* 提取出来。于是我们可以得到这列等式：

2S(qpq^*)= (qpq^*) + (qpq^*)^* = qpq^* + qp^*q^*

 

由于四元数的乘法遵循线性规律，我们可以将公因式提出，得到：

q(p+p^*)q^* = q(2S(p))q^* = 2S(p)[注1]

 

又由于四元数乘法也作用于模长（Because multiplication preserves norms,），得到N(p) = N(p')[注2]; 同时因为w没有改变，因此可得N(v) = N(v')。

(

注1:  由于2S(p)为标量，我们可以把它放到前面，得2S(p)qq^*。又因为结论2已经告诉我们，在q[***]q^*这种类型的式子中,q是不是单位四元数都是不影响结果的。因此我们可以将其视作一个单位四元数，这样便有q^* = q^-1， 因此2S(p)qq^* = 2S(p)qq^-1 = 2S(p) 。

注2:  所谓“Because multiplication preserves norms”，我想可以这样理解：因为p' = qpq^*，而因为乘法保留模长，同时我们已把q看作为单位四元数（意味着N(q)=N(q^*)=1），因此有N(p') = N(p)。 再注意到上面刚刚证明了2S(p') = 2S(p)，即意味着w部相同。两个四元数模长相等，其实部又相等，可以不难得到其虚部模长也相等，即N(v) = N(v')。

) 

最后我们来证明结论3 —— 该定理最核心的部分。考虑下图中的情形，图中N(v0) = N(v1) = 1 。 我们定义一个四元数q = v1v0^* = [v0 × v1, v0 · v1][注3] 。我们再定义Ω为v0到v1之间的角度， 所以v0·v1 = cosΩ 。我们再在两向量的叉积方向上再设置一个单位向量 v = (v0 × v1) /‖v0 × v1‖， 该单位向量同时垂直于v0 和v1。现在我们可以将q 写成 [ v sinΩ, cosΩ][注4] （我们应该假设v1 ≠ ±v0, 否则 q =+ 1， 如此这个旋转动作是无效的）（We shall assume v1 ± v0, else q = ±1, and the action is the identity）。

 

(

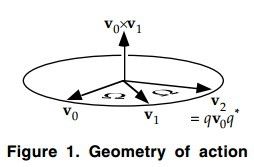
注3:  这里解释一下为什么 v1v0^* = [v0 × v1, v0 · v1]。 根据前面列出的关于四元数的basic facts，我们知道而v0^*= [v0, 0]^* = [-v0, 0] = -v0 。同时还知道vv' = [v×v', -v·v'] ，这里令v = v1, v' = v0^*。 因此得到v1v0^* = (-1)v1v0 =  （-1）[v1 × v0, -v1 · v0] = [v0 × v1, v0 · v1] 。 

注4:  这里解释一下为什么q可以写成 [ v sinΩ, cosΩ]. 至此，我们已经知道q = v1v0^*= [v0 × v1, v0 · v1] 。 很明显v0 · v1 =  cosΩ 。 而又有  v0 × v1 = v · ‖v0 × v1‖。 ‖v0 × v1‖是向量积v0 × v1的模长，根据向量积的求模共识，我们有 ‖v0 × v1‖ = ‖v0‖‖v1‖sinΩ,  因为v0、v1皆为单位向量，所以‖v0 × v1‖ = sinΩ 。 因此 q = [ v sinΩ, cosΩ]  

)

现在我们引入v2, 令v2 = qv0q^*。 

我们可以推导出，v2v1^* = (qv0q^*) v1^* 拥有与v1v0^*一样的结构（内积与外积都相等）；因此v2 = qv0q^* 与v0和v1都共同位于同一个平面内，且v2与v1的夹角也为Ω。

 

下面是推导过程： 首先用q = v1v0^* 将(qv0q^*) v1^* 中q^*的替换，得到(qv0(v1v0^*)^*)v1^*，进一步简化得到q(v0v0)(v1^*v1^*)。因为v0与v1是单位向量，所以它们的平方等于-1[注5]，这样就只剩下了q。

(

注5: 解释下为什么 v0v0 = v1^*v1^* = -1 。假设v是单位向量，同时注意v叉乘自己的结果是0向量，所以vv = [v×v, -v·v] = [0, -1]。 

)

 

用等式可以描述为：

(qv0q^*)v1^*  =   (qv0(v1v0^*)^*)v1^*
                    =   qv0(v0v1^*)v1^*
                    =   q(v0v0)(v1^*v1^*)
                    =    q(-1)(-1)
                    =   v1v0^*

 

所以我们证明了v2v1^* 与v1v0^* 的确是相等的，也同时说明了上图中的描述也是准确的。我们还可以进一步证明，假如那里有个v3 = qv1q*的话，由于q = v1v0* =》v1 = qv0，我们可以推导出 ，q作用于v1 后得到的v3，也仍然与v0,v1,v2在同一个平面上，且据v2的夹角也为Ω。因为：
 

v3v2*  =  (qv1q*) (qv0q*)* 
            =  (q(qv0)q*) (qv0q*)*
            =  q(qv0q*)(qv0q*)*
            =  q

 

联系到我们的定理，我们可以得知，作用在v0以及v1上的四元数q，都是将其绕轴v 旋转2Ω。事实上，这个四元数可以被应用到任意向量p中（而非仅仅v0或者v1），因为任意向量p都可以表示为s0v0+s1v1+s2v。四元数的线性性允许我们独立地检验v0，v1 以及v 。（注：意思是只要它们分别成立了，其线性结合的结果也同样成立）。

 

当然，虽然我们已经证明了q作用于v0以及v1是成立的，但仍需证明对v也是成立的，这样才能证明对任意p有效。现在我们来思考对v的证明。通过观察我们得知，四元数的乘法之所以不满足交换律，就是因为叉积不满足交换律的原因。但在乘积qv = [v sinΩ, cosΩ][v,0]中，其叉乘的结果为0[注6]，所以qv = vq,  进而有qvq* = vqq* = v, 这样也就证明了q对v的作用也是有效的。

(

注6: 联系到 注5，我们不难理解为什么 v × v 的结果为0向量。 

)

因此，现在我们就可以理直气壮地说，四元数q= [v sinΩ , cosΩ] 对任意一个向量的作用就是绕着轴v 旋转2Ω了。这就是定理1中结论3的证明。

 

推论：任意一个在三维空间上的旋转，都是一些单位四元数相作用的结果。

证明：利用定理1结论3，我们可以扩展到任意轴和任意角度，从而得到该推论成立。