平衡树学习笔记（2）——替罪羊树

史上最暴力的平衡树——替罪羊树

前言

​ 想学替罪羊树很久了，刚开始接触平衡树的时候就久仰替罪羊树的大名，但是无奈经验和理解能力都有些欠缺，暂时放了下，这几天题目难度不大，有了时间来学替罪羊树。

大致思路

​ 其实替罪羊树之所以看起来高深，有80%的原因是因为名字的问题，其实我也不知道为什么叫这个名字（好像是说因为一个点导致整棵子树重构）。但是事实上就是把一棵子树拍扁，再重新拎起来来保证平衡（真的好暴力）。

实现部分

（其实我真的没感觉这个暴力的平衡树有多简单，个人感觉比splay还麻烦）

0.前置

1.数组介绍

先讲讲数组的各个数的用途：

struct node
{
    int key,size,bz,l,r,g;
}a[N*2];

key：当前节点的值。

size：当前子树的大小（包括删除的点）。

bz：当前节点是否被删除（删除为0，否则为1）。

l：该节点左子树根节点的编号（左儿子）。

r：该节点右子树根节点的编号（右儿子）。

g：当前子树内还有多少个点没有被删掉。

2.内存池

我们会删去很多节点，所以那些没有用的节点的编号会占据很多空间，于是我们可以建一个内存池（栈）来存储无用的节点编号，方便调用。

int tot=0;
int getnew()
{
	if (z[0])
		return z[z[0]--];
	return ++tot;
}

---

1.重构

​ 先把这个平衡树最特殊的东西讲了…

​ 对于一棵以x为根的子树，我们找到它的中序遍历（左根右），要使它重构之后的中序遍历与原来相等，但是层数减少这样就可以尽量满足树的平衡…

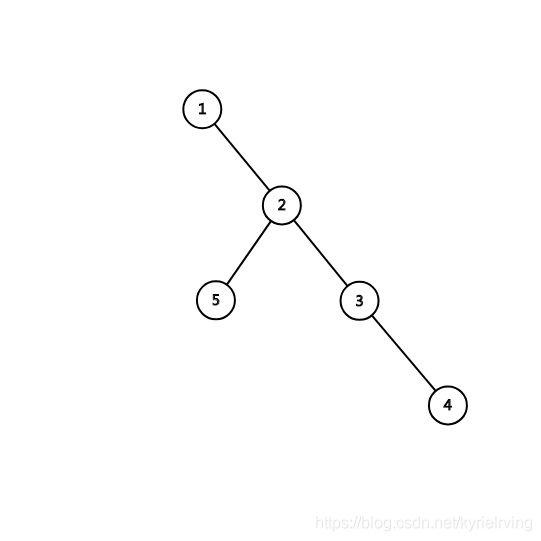
​ 像这样：

我们发现现在这棵树真的好不平衡…

怎么办呢？

我们需要将它先转成一个数组（按照中序遍历）：

1 5 2 3 4

然后就可以愉快地开始重构了：

先将最中间的一个数提出来，作为整棵子树的根（提出2）

接着对于左边的数放到左子树中，右边的数放到右子树中（即1 5放入左子树，2 4放入右子树）

再递归下去即可。

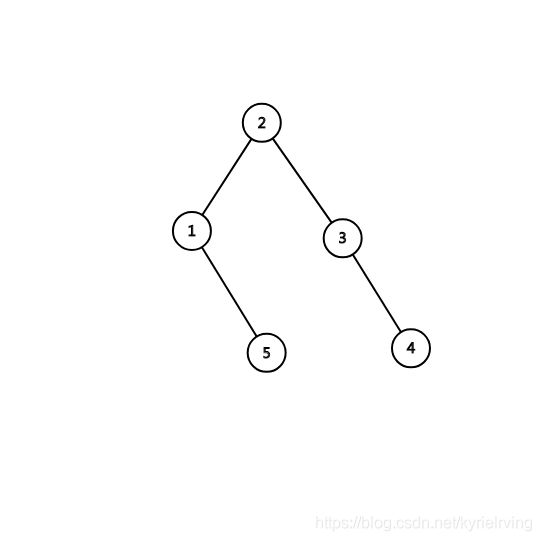
重构完以后就变成了这样：

我们就可以得到一棵尽可能平衡的树。

代码如下：

int get_tmp(int x)//得到中序遍历
{
	if (!x)
		return 0;
	if (a[x].l)
		get_tmp(a[x].l);
	if (a[x].bz)
		tmp[++tmp[0]]=x;
	else
		z[++z[0]]=x;
	if (a[x].r)
		get_tmp(a[x].r);
}
int set(int l,int r,int &x)
{
	int mid=(l+r)/2;
	x=tmp[mid];
	if (l==r)
	{
		a[x].l=a[x].r=0,a[x].size=a[x].g=1,a[x].bz=1;
		return 0;
	}
	(l

---

2.插入

插入几乎跟其他所有平衡树的插入都差不多，如果有问题可以参考上一篇平衡树学习笔记——splay。[^1]

这种做法是直接插入节点：

int insert(int &x,int z)
{
	if (!x)
	{
		x=getnew(),a[x].size=a[x].g=a[x].bz=1,a[x].key=z,a[x].l=a[x].r=0;
		return 0;
	}
	a[x].size++,a[x].g++,(z<=a[x].key)?insert(a[x].l,z):insert(a[x].r,z);//需要注意size和g都要加1
}

---

3.查询

1.查询排名第x的数的值

直接在树上跳就好。

遇到一样的就退出，比当前数大就往右走，否则往左走。

注意一个点是否被删除。

int get_z(int x)
{
	int now=root;
	while (now)
	{
		if (a[now].bz&&a[a[now].l].g+1==x)
			return a[now].key;
		if (a[a[now].l].g>=x)
			now=a[now].l;
		else
			x-=a[a[now].l].g+a[now].bz,now=a[now].r;
	}
}

2.查询值为x的数的排名

我们可以从根节点出发，向下搜索，每次如往右子树走，则将答案加上左子树以及本身的值。

记住一开始ans要为1（没有排名为0的点）。

int get_rk(int x)
{
	int ans=1,now=root;
	while (now)
	{
		if (a[now].key>=x)
			now=a[now].l;
		else
			ans+=a[now].bz+a[a[now].l].g,now=a[now].r;
	}
	return ans;
}

---

4.删除

这个可以说是替罪羊树如此暴力的源泉了。

因为在替罪羊树中，我们对于删除的点只打上标记（由于删除时的懒惰，我们在后面需要重构），操作时直接跳过。

代码也很懒惰（言简意赅才怪）：

int del_rk(int &x,int rk)
{
	a[x].g--;
	if (a[x].bz&&a[a[x].l].g+1==rk)	
	{
		a[x].bz=0;
		return 0;
	}
	(a[a[x].l].g+a[x].bz>=rk)?del_rk(a[x].l,rk):del_rk(a[x].r,rk-a[a[x].l].g-a[x].bz);
}
int del_z(int v)
{
	del_rk(root,get_rk(v));//这句话比较难理解，删除值为v的数，就是先找出v的排名，再删除排名为...的数
	if ((double)a[root].size*al>a[root].g)//判断删除完是否需要重构
		rebuild(root);
}

---

5.判断重构

这一块决定了替罪羊树的时间的多边性。

我们设alpha（在程序中是al）表示：

1. 我们需要一棵子树内的有用节点（即标记为1的点至少占多少）。
2. 这棵树的左子树或者右子树最多占整棵子树的多少。

当然，我们可以将这两个数分开（但是我的程序里是将其合在了一起）。

我们可以看到，在上面del_z的函数内我们就用了al的第一个作用。

那么在我们插入数之后（即调用insert函数之后），我们就需要用到alpha来判断这棵替罪羊树是否需要重新平衡节点。

我们设pd函数表示根为x的节点，在插入了值为y的数之后是否需要重构。

那么我们就从x节点开始顺次下去，直到y节点。

注意我们要从上到下，遇到需要重构的子树重构完之后就直接退出，因为这样我们已经构出了一棵相对平衡的树，不需要继续下去重构。

另外，那个bc函数表示判断该子树时候平衡。

int bc(int x){return (double)a[x].g*al>max(a[a[x].l].g,a[a[x].r].g);}
int pd(int x,int y)
{
	int f=(y>a[x].key)?a[x].r:a[x].l;
	while (f)
	{
		if (!bc(f))
		{
			rebuild((y>a[x].key)?a[x].r:a[x].l);
			return 0;
		}
		x=f,f=(y>a[x].key)?a[x].r:a[x].l;
	}
}

---

就那么多了吗？

并不，以上只是很基本的几个操作，具体的话应该大部分功能都可以靠上述函数交替调用实现。

6.综合运用

1.插入

跟上面讲的一样，插入完之后直接判断是否需要重构。

int yroot=root;
insert(root,x);
pd(yroot,x);

2.删除

没什么好说的，直接调用del_z函数就好了。

3.查询

直接输出就好了。

4.查找前驱

我们先要找到x的排名，再查找排名为x的排名-1的数的值。

int u=get_rk(x)-1;
printf("%d\n",get_z(u));

5.查找后继

道理差不多，自行理解。

int u=get_rk(x+1);
printf("%d\n",get_z(u));

一些废话

其实我个人觉得替罪羊树不是特别实用（大佬勿喷）

它跟splay比的优点就是：

1. 比较易懂，不用转来转去，不会烧脑。
2. 常数小（吧）…
3. 可以手动调al的值，让它可以控制重构的次数，以在某些数据有特殊情况的题中暴力出奇迹。

另外，下面讲一讲关于al的值的调整方法（al的值应在(0.5,1)）：

首先，我们要明白，当重构的次数少的时候，树内无用的节点就会多，树也会不平衡，但是如果重构次数过多，我们重构需要的时间也就无法保证，可能会退化成暴力。

在询问较多，我们可以将al设小一点，这样重构次数会多，查询用的时间也就少了。

在修改较多时，al要调大一点，以保证重构次数较少。

总结

其实平衡树这种东西，还是要多做题目多练手，这样才不会生疏。

（中考加油！）