CNN的基本概念、常用的计算公式和pytorch代码

---

一、CNN的基本概念

卷积填充池化参考此处
激活函数参考此处
简言之：
卷积有助于我们找到特定的局部图像特征。
池化是用于特征融合和降维，还可以防止过拟合。
激活函数是增加非线性，主要是为了解决梯度消失和梯度爆炸问题。

二、常见的卷积

参考此处

1.一般卷积

这个就是最常见的卷积了，看动图比较容易理解。

2.扩张卷积(空洞卷积)

这个主要用来扩大感受野，改变扩张率可获得多尺度信息。

3.转置卷积(反卷积)

就是卷积的逆过程做还原(恢复尺寸不恢复值)，比如要可视化、分割还原、gan生成等。

4.可分离卷积

可分离卷积主要可分为空间可分离卷积和深度可分离卷积。

4.1.空间可分离卷积

用2个1D卷积核代替1个2D卷积核得到同样的结果，这样减少了计算量。

4.2.深度可分离卷积

对N通道分别进行卷积后，再对这个输出做一个pointwise核(11N)卷积，这样也减少了计算量。

11的卷积核可以降维、增加模型深度以及增加非线性。
NN的卷积核可以

三、CNN的输入输出尺寸计算公式

3.1.卷积层

N=(W-F+2P)/S + 1
其中
N：输出大小
W：输入大小
F：卷积核大小
P：填充值的大小
S：步长大小
如当W=256，F=3，P=1，S=2时，N=(256-3+2*1)/2+1=128

3.2.池化层

N=(W+2P-D(F-1)-1)/S + 1
其中
N：输出大小
W：输入大小
D：空洞
F：池化核大小
P：填充值的大小
S：步长大小*
如当W=128，D=0， F=2，P=0，S=2时，N=(128+0-0-1)/2+1=64
当分子为奇数时，无论分母是1还是2，分子在最后算的时候都会取为偶数

四、CNN常用的激活函数

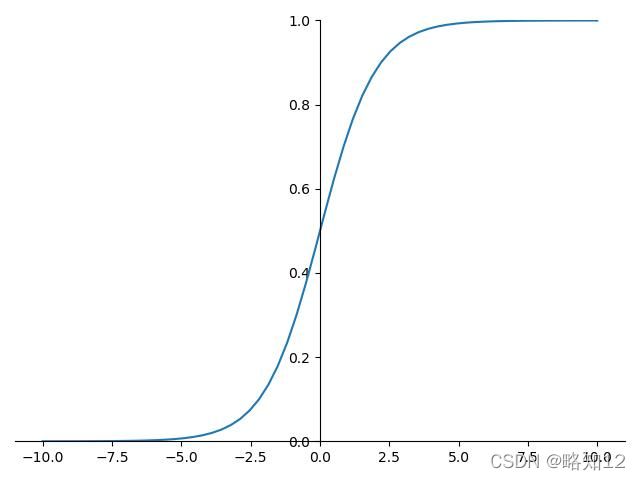
4.1.Sigmoid

计算公式：

函数图像：

导数图像：

4.2.tanh

计算公式：
函数图像：

导数图像：

4.3.Relu

计算公式：

函数图像：

导数图像：

此外，还有LeakRelu、ERelu、Silu等。

五、标准化和归一化

参考此处

1.标准化

将数据变换为均值为0，标准差为1的分布

1.1.批标准化(Batch Normalization)

每个激活函数都有自己的非饱和区，在激活函数前如果没有BN的话，在非饱和区外的数据都会导致梯度消失，只有非饱和区的数据可用，也加快收敛，防止了过拟合，所以一般会在激活函数前加入BN。

2.归一化

将数据变换到某个区间范围，如[0,1]

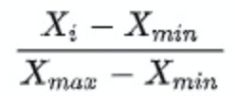
总结：归一化是根据极小极大值缩放范围的，从这个定义出发，看自己的数据是否需要这样处理
标准化相比更常见，如在梯度计算时能加快收敛速度，处理不同尺度的特征等

六、保存和加载模型

1.仅保存学习到的参数

1.1.保存模型：torch.save(model.state_dict(), PATH)

1.2.调用模型：model.load_state_dict(torch.load(PATH))；model.eval()

2.保存整个model

2.1.保存模型：torch.save(model,PATH)

2.2.调用模型：model = torch.load(PATH)

七、model.eval()和with torch.no_grad()的作用和区别

参考此处
在train模式下，dropout网络层会按照设定的参数p设置保留激活单元的概率（保留概率=p); batchnorm层会继续计算数据的mean和var等参数并更新。

在val模式下，dropout层会让所有的激活单元都通过，而batchnorm层会停止计算和更新mean和var，直接使用在训练阶段已经学出的mean和var值

model.eval()中的数据不会进行反向传播，但是仍然需要计算梯度。
with torch.no_grad()中的数据不需要计算梯度，也不会进行反向传播。

可以看到测试要用model.eval()模式，加上with torch.no_grad()能更节省计算资源。

八、Copy

赋值：内存地址不变，相当于引用，一改都改。
copy.copy()：浅复制，增加元素没影响，但改变共有的元素则原数据也改变。
copy.deepcopy()：深复制，就是完全复制，包括内存地址都是新的。

九、微调

参考此处
什么情况下可以微调呢？
（1） 你要使用的数据集和预训练模型的数据集相似
（2） 自己搭建或者使用的CNN模型正确率太低。
（3）数据集相似，但数据集数量太少。
（4）计算资源太少。
根据自己的数据判断是否需要预训练

针对不同情况，也有不同的微调方式：
数据集1 - 数据量少，但数据相似度非常高 - 在这种情况下，我们所做的只是修改最后几层或最终的softmax图层的输出类别。

数据集2 - 数据量少，数据相似度低 - 在这种情况下，我们可以冻结预训练模型的初始层（比如k层），并再次训练剩余的（n-k）层。由于新数据集的相似度较低，因此根据新数据集对较高层进行重新训练具有重要意义。

数据集3 - 数据量大，数据相似度低 - 在这种情况下，由于我们有一个大的数据集，我们的神经网络训练将会很有效。但是，由于我们的数据与用于训练我们的预训练模型的数据相比有很大不同。使用预训练模型进行的预测不会有效。因此，最好根据你的数据从头开始训练神经网络（Training from scatch）

数据集4 - 数据量大，数据相似度高 - 这是理想情况。在这种情况下，预训练模型应该是最有效的。使用模型的最好方法是保留模型的体系结构和模型的初始权重。然后，我们可以使用在预先训练的模型中的权重来重新训练该模型。

1.冻结

参考此处
冻结就是让某些层不反向传播：

for layer in list(model.parameters())[:]:#这里就写你要要冻结的层
	layer.requires_grad = False #这里不计算梯度
optimizer = optim.Adam(filter(lambda p: p.requires_grad, model.parameters()), lr=0.0001)#过滤掉不需要反向传播的层

解冻：

for layer in list(model.parameters())[:]:
    layer.requires_grad = True
	optimizer.add_param_group({'params': layer})

2.修改层

查看model的结构后，得到的是
model(
    (feature):Sequential(
        (0):Conv(
        (conv):Conv2d(3,24,kernel_size=(3,3),stride=(2,2),padding=(1,1),bias=False)
        …
        )
        …
        …
    (fc):Sequantial(
        (0):Dropout(p=0.3,inplace=True)
        (1):Linear(in_features=1792,out_features=1000,bias=True)
        )
    )

比如你要修改fc层，类别从1000改为10：

model.fc = nn.Linear(1792,10)

那么输出的fc层就是
(fc):Sequantial(
    (0):Dropout(p=0.3,inplace=True)
    (1):Linear(in_features=1792,out_features=1000,bias=True)

十、评价指标

参考此处
TP: 预测为1(Positive)，实际也为1(Truth-预测对了)
TN: 预测为0(Negative)，实际也为0(Truth-预测对了)
FP: 预测为1(Positive)，实际为0(False-预测错了)
FN: 预测为0(Negative)，实际为1(False-预测错了)
总样本数为：TP+TN+FP+FN

一般直接看到的是准确率Accuracy=(TP+TN)/(TP+TN+FP+FN)

查准率Precision = TP/(TP+FP)

查全率Recall = TP/(TP+FN)

F1 = 2*(PrecisionRecall)/(Precision+Recall)=2TP/(2*TP+FP+FN)
AR = TP/(TP+FP)