机器学习——特征工程——对数转换、Box-Cox转换

一、对数转换

1、概念

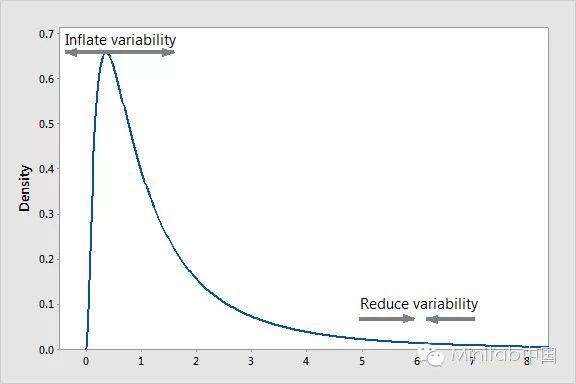
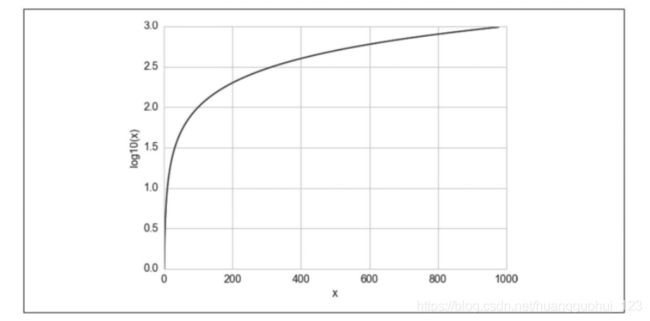
对数函数可以对大数值的范围进行压缩，对小数值的范围进行扩展。x越大，log(x)增长得越慢。如对下图一这个分布进行对数变换，较小数据之间的差异将会变大(因为对数函数的斜率很大)，而较大数据之间的差异将减少(因为该分布中较大数据的斜率很小)。如果你拓展了左尾的差异，减少了右尾的差异，结果将是方差恒定、形状对称的正态分布(无论均值大小如何)。

 我们以如下数据为例。

biz_file = open('精通特征工程/精通特征工程/data/yelp_academic_dataset_business.json')
biz_df = pd.DataFrame([json.loads(x) for x in biz_file.readlines()])
biz_file.close()

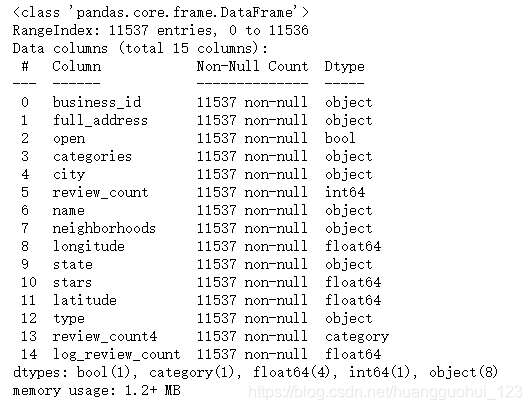
biz_df.info()

输出：

 

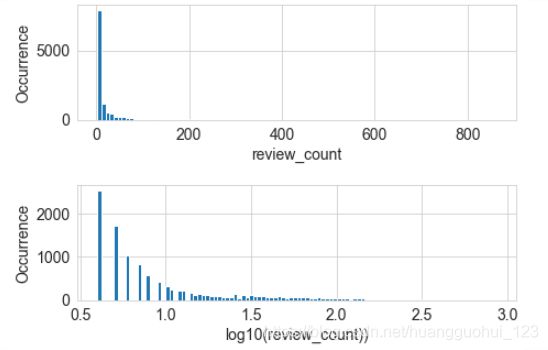
下面比较了对数变换前后的Yelp商家点评数量的直方图：

fig, (ax1, ax2) = plt.subplots(2,1)
fig.tight_layout(pad=0, w_pad=4.0, h_pad=4.0)
biz_df['review_count'].hist(ax=ax1, bins=100)
ax1.tick_params(labelsize=14)
ax1.set_xlabel('review_count', fontsize=14)
ax1.set_ylabel('Occurrence', fontsize=14)

biz_df['log_review_count'] = np.log10(biz_df['review_count'] + 1)  #np.log表示以e为底，np.log10表示以10w为底，加上1的目的是因为真数为0公式没有意义。
biz_df['log_review_count'].hist(ax=ax2, bins=100) 
ax2.tick_params(labelsize=14)
ax2.set_xlabel('log10(review_count))', fontsize=14)
ax2.set_ylabel('Occurrence', fontsize=14)

输出：

从上图的比较可以看出：区间(0.5 ,1]中的箱体间隔很大，是因为在1和10之间只有10个可能的整数计数值，越往后的对数区间可能包含的整数计数值越多。请注意，初始的点评数量严重集中在低计数值区域，但有些异常值跑到了800之外。经过对数变换之后，直方图在低计数值的集中趋势被减弱了，在x轴上的分布更均匀了一些。

2、案例：对数变换在监督式学习中的应用

使用在线新闻流行度数据集中经对数变换后的单词个数预测文章流行度。因为两个预测的输出都是连续型数值，所以我们可以使用简单线性回归来构造模型。我们使用scikit-learn，分别在进行了对数变换和未进行对数变换的特征上进行10-折交叉验证的线性回归。我们使用分数来评价模型，它衡量的是训练出的回归模型预测新数据的能力。良好的模型会有较高的分数。完美的模型能得到的最大分数是1。分数可以是负的，一个糟糕的模型可以得到任意低的负分。通过交叉验证，我们不仅能得到分数的估计值，还能得到它的方差，这有助于我们判断两种模型之间的差异是否是有意义的。关于的计算公式以及什么情况下为负数详细可见《统计推断——假设检验——线性回归——R的平方可以为负数》。

2.1、导入在线新闻数据集

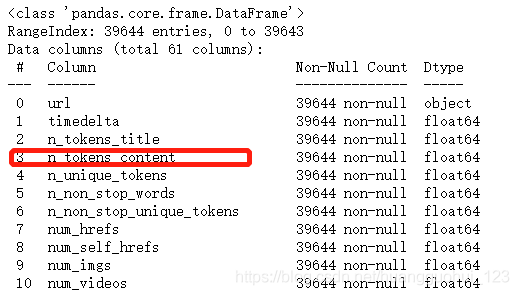
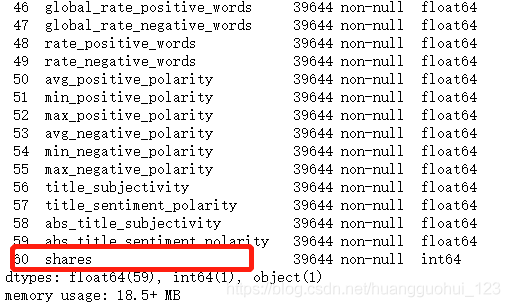
该数据集包括 MasHabor 在两年的时间内出版的 39797 个新闻文章的60个特征，目的是利用这些特征来预测文章在社交媒体上的用分享数量（shares）表示的流行度，在本例中我们将只关注一个特征——文章中的单词数（n_tokens_content）。

import pandas as pd
import numpy as np
import json
from sklearn import linear_model
from sklearn.model_selection import cross_val_score

df = pd.read_csv('精通特征工程/精通特征工程/data/OnlineNewsPopularity.csv', delimiter=', ')
df.info()

输出：

 

..........

2.2、比较对数转换前后的模型拟合效果

#对数转换
df['log_n_tokens_content'] = np.log10(df['n_tokens_content'] + 1)

m_orig = linear_model.LinearRegression()
scores_orig = cross_val_score(
    m_orig, df[['n_tokens_content']], df['shares'], cv=10) #10折交叉验证

m_log = linear_model.LinearRegression()
scores_log = cross_val_score(
    m_log, df[['log_n_tokens_content']], df['shares'], cv=10)

print("R-squared score without log transform: %0.5f (+/- %0.5f)" %
      (scores_orig.mean(), scores_orig.std() * 2))
print("R-squared score with log transform: %0.5f (+/- %0.5f)" %
      (scores_log.mean(), scores_log.std() * 2))

输出：

R-squared score without log transform: -0.00242 (+/- 0.00509)
R-squared score with log transform: -0.00114 (+/- 0.00418)

这两个简单模型（经过对数变换和未经对数变换）对目标变量的预测效果都非常差（为负数），但具有对数变换特征的模型比没有对数变换的表现更好（-0.002421<-0.00114）。

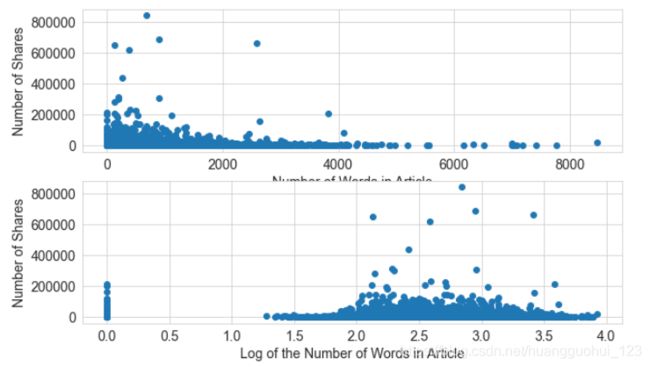
为什么对数转换在这个数据集上更成功？我们可以通过观察输入特征和目标值的散点图来得到线索。

2.3、文章中的单词数（n_tokens_content）和分享数量（shares）相关性的可视化

fig2, (ax1, ax2) = plt.subplots(2, 1,figsize=(10, 6))
fig.tight_layout(pad=0.4, w_pad=4.0, h_pad=6.0)
ax1.scatter(df['n_tokens_content'], df['shares'])
ax1.tick_params(labelsize=14)
ax1.set_xlabel('Number of Words in Article', fontsize=14)
ax1.set_ylabel('Number of Shares', fontsize=14)

ax2.scatter(df['log_n_tokens_content'], df['shares'])
ax2.tick_params(labelsize=14)
ax2.set_xlabel('Log of the Number of Words in Article', fontsize=14)
ax2.set_ylabel('Number of Shares', fontsize=14)

输出：

 

如图所示，对数变换重塑了轴，将目标值（shares）中的大离群值（>200000）进一步拉向轴的右手侧。这就为线性模型在输入特征空间的低值端争取了更多的“呼吸空间”。如果没有进行对数转换，模型就会面临更大的压力，要在输入变化很小（低值端）的情况下去拟合变化非常大的目标值。

二、Box-Cox转换

box-cox变换是统计建模中常用的一种数据变换。上文中的对数变换是它的一个特例。box-cox变换是个变换族。用统计学术语来说，都是方差稳定化变换。要理解为什么方差稳定是个好性质，可以考虑一下泊松分布。 这种变换方法用于连续的因变量不满足正态分布的情况。

关于泊松分布的定义及相关性质可见《统计学基础——常用的概率分布（二项分布、泊松分布、指数分布、正态分布）》

简单的说：泊松分布是一种重尾分布，它的方差等于它的均值。因此，它的均值越大，方差就越大，重尾程度也越大。box-cox可以改变变量的分布，使得方差不再依赖于均值。例如，假设一个随机变量具有泊松分布，如果通过取它的平方根对它进行变换，那么的方差就近似是一个常数，而不是与均值相等。

Box-Cox变换的一般形式为：

式中为经Box-Cox变换后得到的新变量，为原始连续因变量，为变换参数。以上变换要求原始变量取值为正，若取值为负时，可先对所有原始数据同加一个常数使其为正值，然后再进行以上的变换。对不同的所作的变换不同。它包括了平方变换（），平方根变换()，对数变换()和倒数变换()等常用变换。所以Box-Cox变换是一族变换。Box-Cox变换中参数的估计有两种方法：(1)最大似然估计；（2)Bayes方法。通过求解值，就可以确定具体采用哪种变换形式。关于求解值的详细公式推导，大家可以自行查阅相关资料。

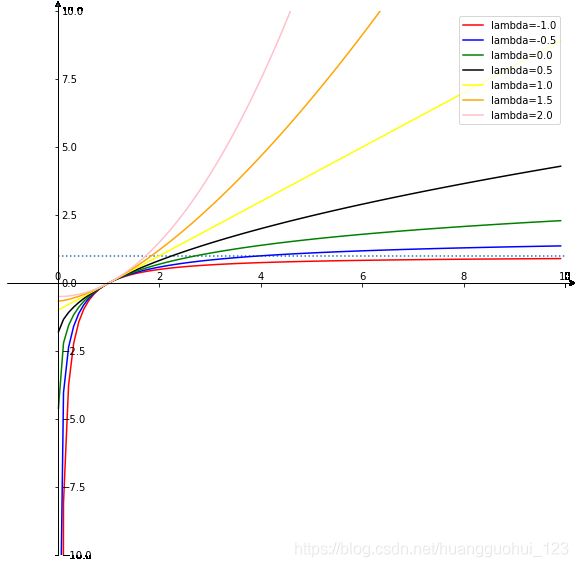
下图展示了从的box-cox变换。

1、定义lambda

from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
#定义lambda
lambdas=np.arange(-1,2.5,0.5)
lambdas

输出：

array([-1. , -0.5,  0. ,  0.5,  1. ,  1.5,  2. ])

2、定义因变量 

X=np.arange(0.01,10,0.1).round(2)
X

输出：

array([0.01, 0.11, 0.21, 0.31, 0.41, 0.51, 0.61, 0.71, 0.81, 0.91, 1.01,
       1.11, 1.21, 1.31, 1.41, 1.51, 1.61, 1.71, 1.81, 1.91, 2.01, 2.11,
       2.21, 2.31, 2.41, 2.51, 2.61, 2.71, 2.81, 2.91, 3.01, 3.11, 3.21,
       3.31, 3.41, 3.51, 3.61, 3.71, 3.81, 3.91, 4.01, 4.11, 4.21, 4.31,
       4.41, 4.51, 4.61, 4.71, 4.81, 4.91, 5.01, 5.11, 5.21, 5.31, 5.41,
       5.51, 5.61, 5.71, 5.81, 5.91, 6.01, 6.11, 6.21, 6.31, 6.41, 6.51,
       6.61, 6.71, 6.81, 6.91, 7.01, 7.11, 7.21, 7.31, 7.41, 7.51, 7.61,
       7.71, 7.81, 7.91, 8.01, 8.11, 8.21, 8.31, 8.41, 8.51, 8.61, 8.71,
       8.81, 8.91, 9.01, 9.11, 9.21, 9.31, 9.41, 9.51, 9.61, 9.71, 9.81,
       9.91])

3、 输出不同下的曲线

#定以曲线颜色
C=['red','blue','green','black','yellow','orange','pink']
#创建画布
fig = plt.figure(figsize=(10,10))
#使用axisartist.Subplot方法创建一个绘图区对象ax
ax = axisartist.Subplot(fig, 111)  
#将绘图区对象添加到画布中
fig.add_axes(ax)
ax.axis[:].set_visible(False)#通过set_visible方法设置绘图区所有坐标轴隐藏
ax.axis["x"] = ax.new_floating_axis(0,0)#ax.new_floating_axis代表添加新的坐标轴
ax.axis["x"].set_axisline_style("->", size = 1.0)#给x坐标轴加上箭头
#添加y坐标轴，且加上箭头
ax.axis["y"] = ax.new_floating_axis(1,0)
ax.axis["y"].set_axisline_style("-|>", size = 1.0)
#设置x、y轴上刻度显示方向
ax.axis["x"].set_axis_direction("top")
ax.axis["y"].set_axis_direction("right")

for i in range(len(lambdas)):
    Y=stats.boxcox(X,lmbda=lambdas[i])
    plt.plot(X,Y, c=C[i],label='lambda=%s'%(lambdas[i]))
    plt.legend()
plt.xlim(-1,10)
plt.ylim(-10,10)
plt.hlines(1,0,10,linestyles='dotted')
plt.legend(loc='upper right')
plt.show()

输出：

 

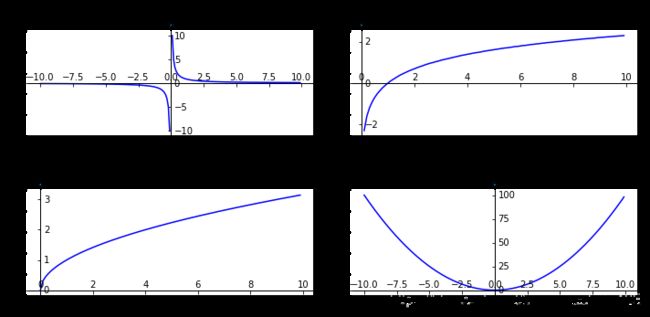
注意，因为输入的因变量必须为正数，所以，在这里我们无法看到完整的数据曲线，我们回顾下我们高中时候，所学的几种常见函数的曲线。

import matplotlib.pyplot as plt  #导入matplotlib库
import numpy as np  #导入numpy库
#创建画布并引入axisartist工具。
import mpl_toolkits.axisartist as axisartist

X=np.arange(-10,10,0.1).round(2)

#画带坐标轴的图像
def createplot(X,Y,i):
    #使用axisartist.Subplot方法创建一个绘图区对象ax
    ax = axisartist.Subplot(fig,2,2,i)
    #将绘图区对象添加到画布中
    fig.add_axes(ax)
    ax.axis[:].set_visible(False)#通过set_visible方法设置绘图区所有坐标轴隐藏
    ax.axis["x"] = ax.new_floating_axis(0,0)#ax.new_floating_axis代表添加新的坐标轴
    ax.axis["x"].set_axisline_style("->", size = 1.0)#给x坐标轴加上箭头
    #添加y坐标轴，且加上箭头
    ax.axis["y"] = ax.new_floating_axis(1,0)
    ax.axis["y"].set_axisline_style("-|>", size = 1.0)
    #设置x、y轴上刻度显示方向
    ax.axis["x"].set_axis_direction("top")
    ax.axis["y"].set_axis_direction("right")
    #在带箭头的x-y坐标轴背景下，绘制函数图像
    #绘制图形
#     plt.xlim(x_min,x_max)
#     plt.ylim(y_min,y_max)
    plt.plot(X,Y, c='b')

Y1=(1/X).round(2)   #lambda=-1
Y2=np.log(X).round(2)  #lambda=0
Y3=X**0.5   #lambda=0.5
Y4=(X**2).round(2) #lambda=2

#创建画布
fig = plt.figure(figsize=(10,5))
ax1=fig.add_subplot(221)
createplot(X,Y1,1)
plt.title('lambda=-1',y =1.1)
ax2=fig.add_subplot(222)
createplot(X,Y2,2)
plt.title('lambda=0',y =1.1)
ax3=fig.add_subplot(223)
createplot(X,Y3,3)
plt.title('lambda=0.5',y =1.1)
ax4=fig.add_subplot(224)
createplot(X,Y4,4)
plt.title('lambda=2',y =1.1)
plt.tight_layout()
plt.show()

输出：

 

小于1时，可以压缩高端值；大于1时，起的作用是相反的。

下面我们通过案例来说明box_cox的运用，仍然以Yelp商家点评数量为例。

• Box-cox变换假定输入数据都必须是正的，所以检查数据的最小值以确定满足需求

from scipy import stats
biz_df['review_count'].min()

输出：

3

•  设置为0，使用对数变化（没有固定长度的位移）

rc_log = stats.boxcox(biz_df['review_count'], lmbda=0)
biz_df['rc_log']=rc_log

• 默认情况下， Scipy在实现Box-Cox转换时，会找出使得输出最接近正态分布的函数

rc_bc, bc_params = stats.boxcox(biz_df['review_count'])
bc_params

输出：

-0.5631160899391674

•  保存Box-Cox转换的结果

biz_df['rc_bc']=rc_bc

•  初始点评数量和变换后（对数转换及Box-Cox转换）点评数量在分布上的可视化比较

fig, (ax1, ax2, ax3) = plt.subplots(3, 1)
fig.tight_layout(pad=0, w_pad=4.0, h_pad=4.0)
# 原始数据
biz_df['review_count'].hist(ax=ax1, bins=100)
ax1.set_yscale('log')
ax1.tick_params(labelsize=14)
ax1.set_title('Review Counts Histogram', fontsize=14)
ax1.set_xlabel('')
ax1.set_ylabel('Occurrence', fontsize=14)

# 对数转换
biz_df['rc_log'].hist(ax=ax2, bins=100)
ax2.set_yscale('log')
ax2.tick_params(labelsize=14)
ax2.set_title('Log Transformed Counts Histogram', fontsize=14)
ax2.set_xlabel('')
ax2.set_ylabel('Occurrence', fontsize=14)

# Box-Cox 转换
biz_df['rc_bc'].hist(ax=ax3, bins=100)
ax3.set_yscale('log')
ax3.tick_params(labelsize=14)
ax3.set_title('Box-Cox Transformed Counts Histogram', fontsize=14)
ax3.set_xlabel('')
ax3.set_ylabel('Occurrence', fontsize=14)

输出：

二、概率图（QQ图）

概率图（probplot）是一种非常简单的可视化方法，用以比较数据的实际分布与理论分布，它本质上是一种表示实测分位数和理论分位数的关系的散点图。

此处所讲的概率图实际上就是QQ图，关于QQ图的原理及详细绘制方法，可见《统计推断——正态性检验（图形方法、偏度和峰度、统计（拟合优度）检验）》中的“图形验证——QQ图”。

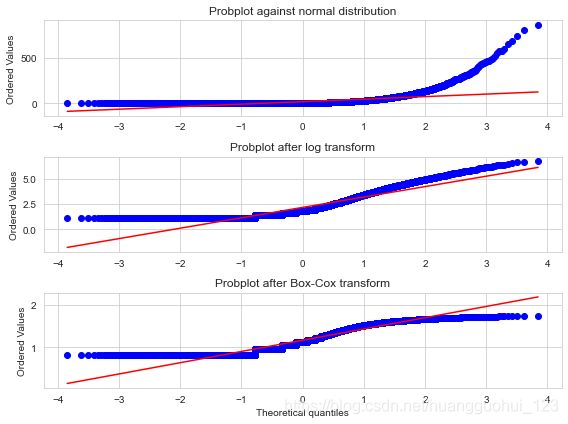
下图展示了Yelp点评数据的三种概率图，分别是初始点评数量、对数变换后点评数量的概率图和Box-Cox变换后点评数量的概率图，并和正态分布进行了对比（红线）。因为观测数据肯定是正的，而高斯分布可以是负的，所以在负数端，实测分位数和理论分位数不可能匹配。因此，我们只关注正数部分。于是，我们可以看出与正态分布相比，初始的点评数量具有明显的重尾特征（排序后的值可以达到4000以上，而理论分位数只能到达4左右）。普通对数变换和最优Box-Cox变换都可以将正尾部拉近正态分布。根据图形明显可以看出，相比对数变换，最优Box-Cox变换对尾部的压缩更强，它使得尾部变平，跑到了红色等值斜线下面。

from scipy import stats

fig2, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(8, 6))
# fig.tight_layout(pad=4, w_pad=5.0, h_pad=0.0)
prob1 = stats.probplot(biz_df['review_count'], dist=stats.norm, plot=ax1)
ax1.set_xlabel('')
ax1.set_title('Probplot against normal distribution')
prob2 = stats.probplot(biz_df['rc_log'], dist=stats.norm, plot=ax2)
ax2.set_xlabel('')
ax2.set_title('Probplot after log transform')
prob3 = stats.probplot(biz_df['rc_bc'], dist=stats.norm, plot=ax3)
ax3.set_xlabel('Theoretical quantiles')
ax3.set_title('Probplot after Box-Cox transform')
plt.tight_layout()
plt.show()

输出：