人工智能-机器学习&人工神经网络
机器学习
机器学习部分主要学习的内容是朴素贝叶斯算法和决策树算法。
机器学习研究计算机如何模拟人类的学习行为，获取新的知识或新的技能，重新组织已有知识改善自身性能，使得计算机具有人的学习能力，从而实现人工智能。
机器学习常分类为：
- 监督学习：已知输入和输出的情况下建立输入到输出的映射，常用于分类和回归任务
- 无监督学习：没有正确输出，只有输入，模型自行归纳数据的特征信息，常用于聚类任务
- 强化学习：Agent选择一个动作作用于环境，环境给出一个强化信号和改变后的状态，Agent根据强化信号和环境当前状态选择下一个行动，选择使收到正强化概率增大的行动
决策树算法
决策树算法是机器学习中常用的一种分类算法，在决策树中，使用各个属性进行分类，选取每次分类的属性的方式有多种。最简单的是ID3算法，使用信息增益作为选择属性的依据。
- 熵：熵表示事物的混乱程度，熵越大表示混乱程度越大，熵越小表示混乱程度越小。对于随机事件S，如果有N种可能，每种可能出现的概率为Pi，则该事件的熵为：
H ( S ) = − ∑ i = 1 N p i log 2 p i H(S) = -\sum_{i=1}^Npi \log_2pi H(S)=−i=1∑Npilog2pi - 信息增益：信息增益表示特征A的信息对类D的信息的不确定性的减少程度，是类未按某个属性划分的熵减去按照某个属性不同取值划分的熵的平均值。定义为：
G a i n ( D , A ) = H ( D ) − ∑ i = 1 V ∣ D i ∣ ∣ D ∣ H ( D i ) Gain(D,A) = H(D) - \sum_{i=1}^V\frac{|D_i|}{|D|}H(D_i) Gain(D,A)=H(D)−i=1∑V∣D∣∣Di∣H(Di)
其中Di是在属性A上取值为Ai的样本，属性A的取值共有V种。
构建决策树时，选取信息增益最大的属性作为划分样本的属性，对样本进行一次划分后，再计算各个属性的信息增益，继续进行划分，直到所有属性都被使用或样本被完全划分。
题
a) 概念题
b)
计算各个属性的信息增益构建决策树：
H ( 吸引力 ) = − 1 2 l o g 2 1 2 − 1 2 l o g 2 1 2 = 1 H(吸引力) = -\frac{1}{2}log_2\frac{1}{2}-\frac{1}{2}log_2\frac{1}{2}=1 H(吸引力)=−21log221−21log221=1
温度一共有2种取值，各占一半，每种中有吸引力的分别占2/5(热)和3/5(冷)
H ( 吸引力 ∣ 温度 ) = 1 2 ( − 2 5 l o g 2 2 5 − 3 5 l o g 2 3 5 ) + 1 2 ( − 2 5 l o g 2 2 5 − 3 5 l o g 2 3 5 ) = 0.971 H(吸引力|温度) = \frac{1}{2}(-\frac{2}{5}log_2\frac{2}{5}-\frac{3}{5}log_2\frac{3}{5}) + \frac{1}{2}(-\frac{2}{5}log_2\frac{2}{5}-\frac{3}{5}log_2\frac{3}{5}) = 0.971 H(吸引力∣温度)=21(−52log252−53log253)+21(−52log252−53log253)=0.971
口味一共有3种取值，甜酸咸4:3:3，每种中有吸引力的分别占1/2、1、0
H ( 吸引力 ∣ 口味 ) = 0.4 ( − 0.5 l o g 2 0.5 − 0.5 l o g 2 0.5 ) + 0 + 0 = 0.4 H(吸引力|口味) = 0.4(-0.5log_20.5-0.5log_20.5) + 0 + 0 = 0.4 H(吸引力∣口味)=0.4(−0.5log20.5−0.5log20.5)+0+0=0.4
份量有2种取值，各占一半，每种中有吸引力的分别占1/5(大)和4/5
H ( 吸引力 ∣ 份量 ) = 0.5 ( − 0.2 l o g 2 0.2 − 0.8 l o g 2 0.8 ) + 0.5 ( − 0.2 l o g 2 0.2 − 0.8 l o g 2 0.8 ) = 0.722 H(吸引力|份量) = 0.5(-0.2log_20.2-0.8log_20.8)+0.5(-0.2log_20.2-0.8log_20.8) = 0.722 H(吸引力∣份量)=0.5(−0.2log20.2−0.8log20.8)+0.5(−0.2log20.2−0.8log20.8)=0.722
可计算各个属性的信息增益为：
G a i n ( 吸引力，温度 ) = 1 − 0.971 = 0.029 G a i n ( 吸引力，口味 ) = 1 − 0.4 = 0.6 G a i n ( 吸引力，份量 ) = 1 − 0.722 = 0.278 Gain(吸引力，温度) = 1-0.971 = 0.029\\ Gain(吸引力，口味) = 1-0.4 = 0.6\\ Gain(吸引力，份量) = 1-0.722 = 0.278 Gain(吸引力，温度)=1−0.971=0.029Gain(吸引力，口味)=1−0.4=0.6Gain(吸引力，份量)=1−0.722=0.278
因此应该选择口味作为对样本划分的属性，对样本进行划分。划分后发现口味为酸和咸的样本已经划分完毕，而甜的样本明显可以再被份量划分为两类，因此直接选取份量继续划分，就可以得到最终的决策树：
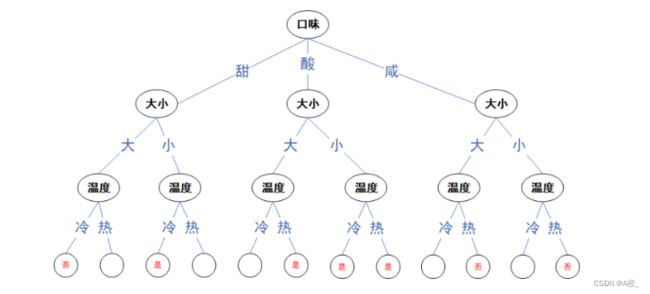
c)
通过查询决策树，可以预测得到“否”的结果。
朴素贝叶斯算法
朴素贝叶斯算法常用来实现分类器，用训练样本得到特定类别下具有某个特征的概率，计算在某个特征条件下样本属于特定类别的概率，对于需要分类的样本，按照特征计算属于每个类别的概率，选择概率最大的作为分类结果。
题
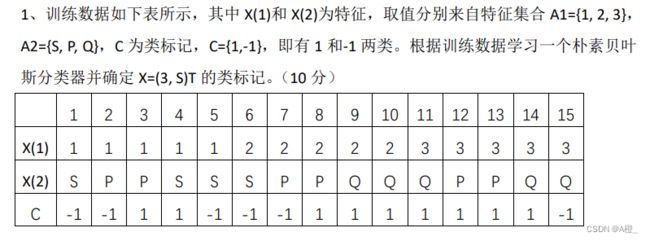首先计算出各个类别下取各个特征的概率：(根据答案，可以只计算需要用到的)
P(C=1) = 9/15
P(C=-1) = 6/15
P(X1=1|C=1) = 2/9
P(X1=2|C=1) = 3/9
P(X1=3|C=1) = 4/9
P(X1=1|C=-1) = 3/6
P(X1=2|C=-1) = 2/6
P(X1=3|C=-1) = 1/6
P(X2=S|C=1) = 1/9
P(X2=P|C=1) = 4/9
P(X2=Q|C=1) = 4/9
P(X2=S|C=-1) = 3/6
P(X2=P|C=-1) = 2/6
P(X2=Q|C=-1) = 1/6
计算所求概率:
P ( C = 1 ∣ X 1 = 3 , X 2 = S ) = α P ( X 1 = 3 , X 2 = S ∣ C = 1 ) = α P ( X 1 = 3 ∣ C = 1 ) P ( X 2 = S ∣ C = 1 ) = 0.0296 α P ( C = − 1 ∣ X 1 = 3 , X 2 = S ) = α P ( X 1 = 3 , X 2 = S ∣ C = − 1 ) = α P ( X 1 = 3 ∣ C = − 1 ) P ( X 2 = S ∣ C = − 1 ) = 0.333 α P(C=1|X1=3,X2=S) = αP(X1=3,X2=S|C=1) = αP(X1=3|C=1)P(X2=S|C=1) \\ = 0.0296α \\ P(C=-1|X1=3,X2=S) = αP(X1=3,X2=S|C=-1) = αP(X1=3|C=-1)P(X2=S|C=-1) \\ =0.333α P(C=1∣X1=3,X2=S)=αP(X1=3,X2=S∣C=1)=αP(X1=3∣C=1)P(X2=S∣C=1)=0.0296αP(C=−1∣X1=3,X2=S)=αP(X1=3,X2=S∣C=−1)=αP(X1=3∣C=−1)P(X2=S∣C=−1)=0.333α
因此分类器预测该样本的类别为C=-1。
此处 αP(X1=3,X2=S|C=1) 可以直接写为 αP(X1=3|C=1)P(X2=S|C=1)的原因是朴素贝叶斯算法采用条件独立假设，假设所有特征之间是独立的，进行了简化。
人工神经网络
人工神经网络部分主要的内容是人工神经网络的原理、感知器算法、多层神经网络
感知器算法
感知器算法的目标是最小化损失函数，学习出模型中的参数w和b，找到将样本划分的分离超平面。
输入到输出的映射关系如下：
Y = F ( w 1 x 1 + w 2 x 2 − θ ) Y = F(w1x1+w2x2-θ) Y=F(w1x1+w2x2−θ)
F是激活函数，取阶跃函数，小于0时为0，大于0时取1。
对感知器进行训练时，假设训练轮次为i，学习率为α，每次计算出误差E(i)，调整参数：
E ( i ) = d ( i ) − y ( i ) w 1 ( i + 1 ) = w 1 ( i ) + α E ( i ) x 1 ( i ) w 2 ( i + 1 ) = w 2 ( i ) + α E ( i ) x 2 ( i ) θ ( i + 1 ) = θ ( i ) + α E ( i ) ( − 1 ) E(i)=d(i)-y(i) \\ w_1(i+1)=w1(i)+αE(i)x_1(i) \\ w_2(i+1)=w2(i)+αE(i)x_2(i) \\ θ(i+1) = θ(i)+αE(i)(-1) E(i)=d(i)−y(i)w1(i+1)=w1(i)+αE(i)x1(i)w2(i+1)=w2(i)+αE(i)x2(i)θ(i+1)=θ(i)+αE(i)(−1)
其中d(i)是第i轮的理想输出，参数调整的部分实际上是：学习率x损失函数在参数上的梯度的相反数，而损失函数在参数上的梯度用链式求导法则得出为：
∂ L ∂ w 1 = ∂ L ∂ O × ∂ O ∂ y × ∂ y ∂ w 1 \frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial O} \times \frac{\partial O}{\partial y} \times \frac{\partial y}{\partial w_1} ∂w1∂L=∂O∂L×∂y∂O×∂w1∂y
其中损失函数通常取：
L O S S = 1 2 ( 正确输出 − 实际输出 ) 2 求导得 ∂ L ∂ O = − ( 正确输出 − 实际输出 ) LOSS = \frac{1}{2} (正确输出 - 实际输出)^2 \\ 求导得 \frac{\partial L}{\partial O} = -(正确输出-实际输出) LOSS=21(正确输出−实际输出)2求导得∂O∂L=−(正确输出−实际输出)
而阶跃函数无法求导，因此在感知器算法中，不乘阶跃函数对加权结果的求导，因此只剩下：
y = w 1 x 1 + w 2 x 2 − θ 求导得 ∂ y ∂ w 1 = x 1 y = w1x1+w2x2-\theta \\ 求导得\frac{\partial y}{\partial w_1} = x_1 y=w1x1+w2x2−θ求导得∂w1∂y=x1
因此最终调整参数的计算方式为
w 1 ( i + 1 ) = w 1 ( i ) + α × − ( − ( 正确输出 − 实际输出 ) × x 1 ( i ) ) = w 1 ( i ) + α E ( i ) x 1 ( i ) w_1(i+1)=w1(i)+α\times -(-(正确输出-实际输出) \times x_1(i)) =w1(i)+αE(i)x_1(i) w1(i+1)=w1(i)+α×−(−(正确输出−实际输出)×x1(i))=w1(i)+αE(i)x1(i)
其中α后面乘的是梯度的反方向，所以最后变成了乘E(i)x1(i)。求θ的调整方式类似。
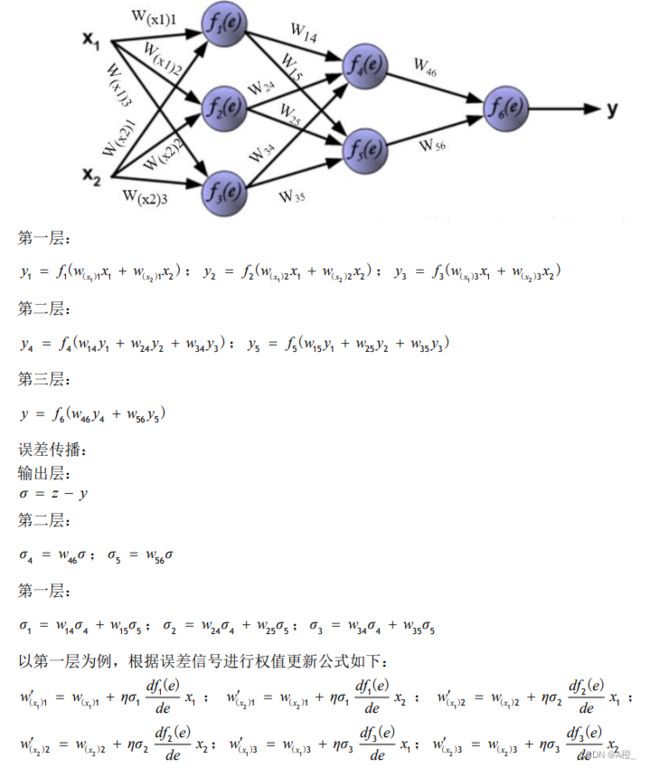
人工神经网络
这部分内容核心是梯度下降原理和误差反向传播的计算，其实在深度学习的PPT部分讲的更清楚。主要学会求误差反向传播的公式。
题
(2)
