电子技术——通路晶体管逻辑
电子技术——通路晶体管逻辑
一个原理上较为简单的逻辑电路的实现可以由多个开关组成,开关受到逻辑输入的控制,如图:
其中CMOS实现我们称为 CMOS 传输门 配置。因为这种逻辑电路是串联在输入输出两端,并且控制着输入输出的关断,即导通或者阻断信号的传输,被称为 通路晶体管逻辑PTL 。
设计思想
PTL电路设计的重点在于确保每时每刻每个电路中的节点要么存在对地的低阻抗通路要么存在对 V D D V_{DD} VDD 的低阻抗通路。为了说明这一点,考虑下面的电路:

其中,开关 S 1 S_1 S1 在反相器输出 A A A 和 输出节点 Y Y Y 之间,受到逻辑变量 B B B 的控制, Y Y Y 输出到另一个反相器中。现在,如果 B B B 是高电平, S 1 S_1 S1 导通,则 Y = A Y = A Y=A ,此时节点 Y Y Y 要么是通地的,要么是通 V D D V_{DD} VDD 的。但是如果 B B B 是低电平, S 1 S_1 S1 截止会怎样?显然,此时 Y Y Y 成为了一个高阻抗节点。如果初始时刻 v Y v_Y vY 是零,那么会持续保持零。然而,若 v Y v_Y vY 初始是 V D D V_{DD} VDD ,那么这个电压会被电容 C C C 保持,此时 Y Y Y 并不是逻辑零,也不符合 Y = A B Y = AB Y=AB 的定义。
现在的问题是,需要使得 Y Y Y 节点在 S 1 S_1 S1 截止的时候有一个对地的回路。如图所示:
这里,我们另外引入了开关 S 2 S_2 S2 受到 B ‾ \overline{B} B 的控制。当 S 1 S_1 S1 截止的时候, S 2 S_2 S2 将会导通,给 Y Y Y 一个对地的回路。
NMOS的开关特性
使用一个NMOS实现一个PTL开关电路可以减小晶体管的数量,这确实是一个优点。然而,单个NMOS开关的动态响应却不是很好,为了说明这一点,考虑下面的电路:

输出节点对地的总电容为 C C C ,此时NMOS的输入电平为 V D D V_{DD} VDD 处于导通状态。我们希望分析系统对一个阶跃输入的响应,初始状态我们假设输入电压为零,并且电容完全放电。
当 v I v_I vI 阶跃至 V D D V_{DD} VDD 的时候,此时NMOS处于饱和区,有漏极电流:
i D = 1 2 k n ( V D D − v O − V t ) 2 i_D = \frac{1}{2} k_n (V_{DD} - v_O - V_t)^2 iD=21kn(VDD−vO−Vt)2
观察上式,我们发现当 v O = V D D − V t v_O = V_{DD} - V_t vO=VDD−Vt 的时候 i D = 0 i_D = 0 iD=0 ,在往后将进入截止区,这说明 V O H V_{OH} VOH 并不等于 V D D V_{DD} VDD 而是等于 V D D − V t V_{DD} - V_t VDD−Vt ,而 V t V_t Vt 会受到体效应的影响,假设我们初始时刻 V t = V t 0 V_t = V_{t0} Vt=Vt0 ,那么在结束时刻有可能 V t V_t Vt 是 V t 0 V_{t0} Vt0 的 1.5 倍到 2 倍那么多!
而且,考虑输出端接入一个反相器。较低的 V O H V_{OH} VOH 将会导致CMOS反相器状态转换不完全,这会导致反相器存在静态电流和静态功耗。
下图展示了其另外一种从 V D D V_{DD} VDD 到 0 0 0 的阶跃响应:

我们假设初始 v O = V D D v_O = V_{DD} vO=VDD 。因此在 t = 0 + t=0+ t=0+ 的时候,NMOS处于饱和区,有漏极电流:
i D = 1 2 k n ( V D D − V t ) 2 i_D = \frac{1}{2} k_n (V_{DD} - V_t)^2 iD=21kn(VDD−Vt)2
我们发现此时源极电压为 0 0 0 (因为此时源极和漏极交换了位置),因此不受体效应的干扰,最终 v O v_O vO 将会降低至 v O = V D D − V t v_O = V_{DD} - V_t vO=VDD−Vt 这时候将会进入三极管区,电容继续放电直到 v O = 0 v_O = 0 vO=0 。那么 V O L = 0 V_{OL} = 0 VOL=0 。
提升 V O H V_{OH} VOH 到 V D D V_{DD} VDD
一种基于电路设计的解决方法如图所示:

观察电路图,PTL开关 Q 1 Q_1 Q1 紧接着接入一个CMOS反相器,反相器的输出同时接入到一个PMOS Q R Q_R QR 中, Q R Q_R QR 同时连接到节点 v O 1 v_{O1} vO1 。当 v O 1 v_{O1} vO1 是低电平的时候, v O 2 v_{O2} vO2 则是高电平, Q R Q_R QR 截止。另一方面,若 v O 1 v_{O1} vO1 是高电平的时候但是不等于 V D D V_{DD} VDD ,反相器输出低电平, Q R Q_R QR 导通,提供电流继续给 C C C 充电,直到 v O 1 = V D D v_{O1} = V_{DD} vO1=VDD 。 Q R Q_R QR 扮演了电平恢复的功能,这通常在MOS数字电路中使用。为 Q R Q_R QR 选择宽长比也在设计的考量范围之内,通常情况下,我们令 k r k_r kr 小于 k n k_n kn 。因为 Q R Q_R QR 在电路中不占主要作用,不需要那么大的电流驱动能力。
另外一种解决方案是基于工艺设计的。我们知道 V O H V_{OH} VOH 和 V t n V_{tn} Vtn 相关。我们可以使用 V t n = 0 V_{tn} = 0 Vtn=0 的MOS元件,这称为 零阈值元件 。通过离子注入技术来控制 V t n V_{tn} Vtn 的值,称为 自然元件 。但是仍然存在问题,低阈值元件增加了亚阈值导通强度,增加了静态功耗。
CMOS传输门开关
COMS传输门使用一对互补的MOS开关,具有绝佳的静态和动态性能。这使它不仅是的一个完美的数字开关并且也是一个完美的模拟开关对于数据转换器和开关电容滤波器。
回想一下,NMOS传输门对于低电平是完美的,而高电平是有缺陷的。同样,PMOS开关具有相反的结果。很自然的想到,将这两个组合起来可以互相弥补。
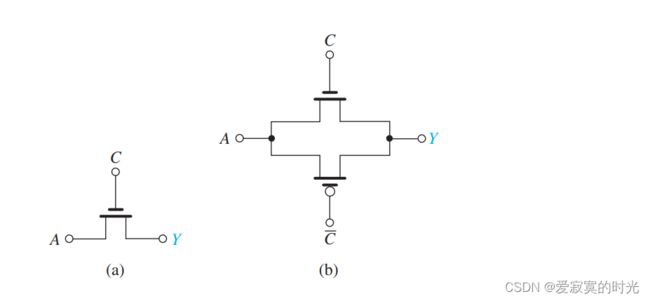
下图展示了CMOS传输门开关,以及其常用的电气符号标识:

首先,当 C = 1 C = 1 C=1 的时候, Y = X Y = X Y=X 。下图展示了这个过程:

之前我们知道,对于NMOS的电流 i D N i_{DN} iDN 会在 v O = V D D − V t n v_O = V_{DD} - V_{tn} vO=VDD−Vtn 处截止。然而,PMOS则不会出现这种情况,PMOS会继续进入三极管区继续给电容充电,从而输出一个完美的高电平。
当阶跃0的时候,如图:

此时 Q N Q_N QN 和 Q P Q_P QP 交换了角色,因此也会输出一个完美的低电平。我们发现,CMOS传输门开关具有比但NMOS开关更好动态和静态性能,代价就是增大了电路的复杂程度和元件数量和总有效电容。
传输门的等效电阻
传输门可也作为电子开关,因为传输门具有有限的闭合电阻,但也绝不是理想的电子开关。有时需要估计传输门的闭合电阻,结合电路的总有效电容来估算传播延迟。
为了计算传输门的闭合电阻,我们以阶跃1的情况为例子。 Q N Q_N QN 直到 v O = V D D − V t n v_O = V_{DD} - V_{tn} vO=VDD−Vtn 都是处在饱和区,之后进入截止区,因此:
i D N = 1 2 k n ( V D D − V t n − v O ) 2 , v O ≤ V D D − V t n i_{DN} = \frac{1}{2} k_n (V_{DD} - V_{tn} - v_O)^2, v_O \le V_{DD} - V_{tn} iDN=21kn(VDD−Vtn−vO)2,vO≤VDD−Vtn
i D N = 0 , v O ≥ V D D − V t n i_{DN} = 0, v_O \ge V_{DD} - V_{tn} iDN=0,vO≥VDD−Vtn
通过 Q N Q_N QN 的总电阻为:
R N e q = V D D − v O 1 2 k n ( V D D − V t n − v O ) 2 , v O ≤ V D D − V t n R_{Neq} = \frac{V_{DD} - v_O}{\frac{1}{2} k_n (V_{DD} - V_{tn} - v_O)^2}, v_O \le V_{DD} - V_{tn} RNeq=21kn(VDD−Vtn−vO)2VDD−vO,vO≤VDD−Vtn
并且:
R N e q = ∞ , v O ≤ V D D − V t n R_{Neq} = \infty, v_O \le V_{DD} - V_{tn} RNeq=∞,vO≤VDD−Vtn
对于 Q P Q_P QP 来说直到 v O = ∣ V t p ∣ v_O = |V_{tp}| vO=∣Vtp∣ 之前都是处在饱和区,之后进入三极管区,因此:
i D P = 1 2 k p ( V D D − ∣ V t p ∣ ) 2 , v O ≤ ∣ V t p ∣ i_{DP} = \frac{1}{2}k_p (V_{DD} - |V_{tp}|)^2, v_O \le |V_{tp}| iDP=21kp(VDD−∣Vtp∣)2,vO≤∣Vtp∣
i D P = k p [ ( V D D − ∣ V t p ∣ ) ( V D D − v O ) − 1 2 ( V D D − v O ) 2 ] , v O ≥ ∣ V t p ∣ i_{DP} = k_p[(V_{DD} - |V_{tp}|)(V_{DD} - v_O) - \frac{1}{2} (V_{DD} - v_O)^2], v_O \ge |V_{tp}| iDP=kp[(VDD−∣Vtp∣)(VDD−vO)−21(VDD−vO)2],vO≥∣Vtp∣
则:
R P e q = V D D − v O 1 2 k p ( V D D − ∣ V t p ∣ ) 2 , v O ≤ ∣ V t p ∣ R_{Peq} = \frac{V_{DD} - v_O}{\frac{1}{2}k_p (V_{DD} - |V_{tp}|)^2}, v_O \le |V_{tp}| RPeq=21kp(VDD−∣Vtp∣)2VDD−vO,vO≤∣Vtp∣
R P e q = V D D − v O k p [ ( V D D − ∣ V t p ∣ ) ( V D D − v O ) − 1 2 ( V D D − v O ) 2 ] , v O ≤ ∣ V t p ∣ R_{Peq} = \frac{V_{DD} - v_O}{k_p[(V_{DD} - |V_{tp}|)(V_{DD} - v_O) - \frac{1}{2} (V_{DD} - v_O)^2]}, v_O \le |V_{tp}| RPeq=kp[(VDD−∣Vtp∣)(VDD−vO)−21(VDD−vO)2]VDD−vO,vO≤∣Vtp∣
最后,总电阻为:
R T G = R N e q ∣ ∣ R P e q R_{TG} = R_{Neq} || R_{Peq} RTG=RNeq∣∣RPeq
显然, R T G R_{TG} RTG 是一个关于 v O v_O vO 的函数。下图是分析曲线:

可以观察到 R T G R_{TG} RTG 可以近似为一个常函数,使用 R T G R_{TG} RTG 在 v O = 0 v_O = 0 vO=0 到 V D D / 2 V_{DD} / 2 VDD/2 之间的平均值可以决定 t P L H t_{PLH} tPLH 。
上述的分析只适用于电容充电过程。对于电容放电过程存在相同的分析方法。
实际上,存在一个估计 R T G R_{TG} RTG 的经验公式为,同时适用于充电和放电过程:
R T G ≃ 12.5 ( W / L ) n k Ω R_{TG} \simeq \frac{12.5}{(W/L)_n} k\Omega RTG≃(W/L)n12.5kΩ
在知道如何估计总电阻之后,就可以对传播延迟进行估计,如图:

这个电路由一个输入反相器,一个中间CMOS传输开关和一个输出反相器组成。我们关系的是信号从 v I v_I vI 到 v O v_O vO 之间的延迟。同样以一个阶跃1为例子。
下图展示了RC分析的等效电路图:

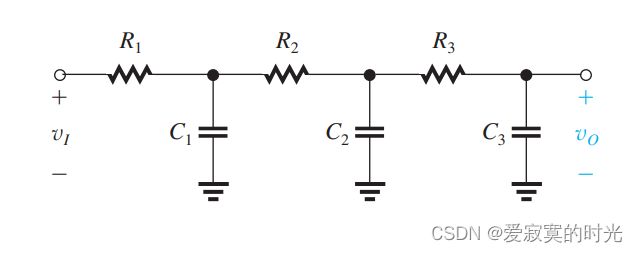
其中 R P 1 R_{P1} RP1 和 R T G R_{TG} RTG 是 Q P 1 Q_{P1} QP1 和传输门的电阻,这里 C o u t 1 C_{out1} Cout1 是输入反相器本身的输出阻抗,而 C T G 1 C_{TG1} CTG1 和 C T G 2 C_{TG2} CTG2 分别是传输门两端的电容, C i n 2 C_{in2} Cin2 是输出反相器的输入电容。观察到这个电路形成了一个RC梯形电路。当然,存在一个简单的式子可以直接计算任意RC梯形电路的传播延迟,这就是 埃尔莫尔延迟公式 。如下图的RC梯形电路:
t P = 0.69 [ C 1 R 1 + C 2 ( R 1 + R 2 ) + C 3 ( R 1 + R 2 + R 3 ) ] t_P = 0.69[C_1 R_1 + C_2 (R_1 + R_2) + C_3(R_1 + R_2 + R_3)] tP=0.69[C1R1+C2(R1+R2)+C3(R1+R2+R3)]
应用埃尔莫尔延迟公式:
t P = 0.69 [ ( C o u t 1 + C T G 1 ) R P 1 + ( C i n 2 + C T G 2 ) ( R P 1 + R T G ) ] t_P = 0.69[(C_{out_1 + C_{TG1}})R_{P1} + (C_{in2 + C_{TG2}})(R_{P1 + R_{TG}})] tP=0.69[(Cout1+CTG1)RP1+(Cin2+CTG2)(RP1+RTG)]
最后,通常假设输入是一个斜坡上升函数而不是完美的阶跃函数,此时可以忽略因子 0.69 。
通路晶体管逻辑的一些例子
下图是一个两路PTL多路选择器,取决于变量 C C C 的值,选择输出是 A A A 还是 B B B 。也就是:
Y = C A + C ‾ B Y = CA + \overline{C}B Y=CA+CB
我们的第二个例子是异或电路,如下图:
与CMOS电路相比,PTL只需要4个晶体管。
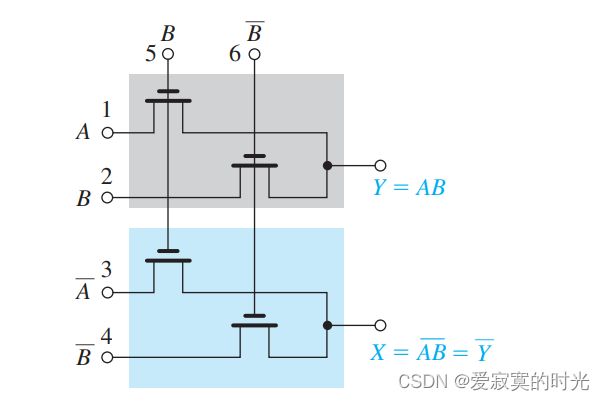
我们最后一个例子如图:
这里使用低或零阈值NMOS元件。观察输入变量和输出变量之间的关系。这个电路称为 互补通路晶体管逻辑 CPL 。这个电路同时实现了AND和NAND逻辑。