使用CNN-LSTM来预测锂离子电池健康状态SOH（附代码）

     对于电动汽车而言，动力锂电池的健康状态(State of Health,SOH)估算方法是电池管理系统中非常重要的一个方面。准确估计锂电池老化状态并预测电池剩余寿命对于电动汽车稳定安全运行有着重要的意义。借助数据驱动方法的思想，本文对锂离子电池寿命历史数据进行分析，通过深度学习方法建立锂电池健康状态评估模型。在模型的选取上，采用长短时记忆循环神经网络(Long short-term memory reccurent neural network LSTM RNN)学习电池的寿命衰减过程，通过迁移学习泛化锂电池SOH评估模型。

     在各种电池特征参数中，电池容量常常被用作表征电池退化的特征。伴随鲤电池充放电循环次数的增加，电池容量会有明显的下降趋势，根据IEEE-1996 标准当电池容量下降到标称容量 80%时，为了保证电池系统安全与稳定运行，建议及时更换新电池。

     尽管理论上循环神经网络可以有效处理时间序列,但随着时间序列的长度增加，网络参数可能会在反向传播的过程中趋近于零或是无穷，这会导致梯度下降或者梯度爆炸，丢失前期的有效信息，从而使得预测准确率下降。因此，出现了一系列改进 RNN 的算法。长短时记忆循环 (LSTM)神经网络就是其中效果较好的一种LSTM 网络通过精妙的门控制将加法运算带入网络中，一定程度上解决了梯度消失的问题。只能说一定程度上，过长的序列还是会出现“梯度消失”，所以 LSTM 叫长一点的“短时记忆”。如图1所示为LSTM单元的结构图。

图1 LSTM单元的结构图

与基础的RNN 所不同的是，LSTM 通过添加复杂的“门”结构来实现过滤几余信息的作用。用于输入信息的叫做“输入门”，用于遗忘的门叫做“遗忘门”，控制输出的叫“输出门”。通过这三个门的逻辑控制单元，LSTM 可以有效决定是否更新或是遗弃某些信息，从而某种程度上克服了容易产生梯度消失和爆炸的缺点。

下面介绍如何使用代码来实现LSTM预测锂离子电池的SOH。

1.首先是程序运行的环境搭建。

举个例子，就比如下面代码的第二行，matplotlib是一个Python的绘图库，它可与 NumPy 一起使用，可以代替Matlab使用。可以将数据进行可视化，使数据更直观。由于其是第三方库，所以需要安装才可以使用。

from SOH_func_scaler import *
import matplotlib.pyplot as pl
from tensorflow import summary as sm
from tensorflow import keras
from keras import models, layers
from keras.callbacks import ModelCheckpoint
from keras.callbacks import TensorBoard
import datetime
import os

2.将图2的电池数据导入，分别将数据赋值给变量FILE_00、FILE_01、FILE_02、FILE_03、FILE_04、FILE_05、FILE_06。同时初始化均方根误差RMSE、绝对误差的平均值MAE、以及迭代次数epoch_index。其中电池数据是以.csv格式保存的，部分数据如图3（有密集恐惧症的可自动忽略该图）所示。其中包括：充电_ _容量(ah),放电容量(ah),累计_容量(ah)、充电_能量(wh)、放电_能量(wh),累计_能量(wh),库仑_ _能量效率(%)、效率(%)、最大_电压(v)、充电_最终电压(v),放电_最终电压(v),单位充电容量(ah / g)、单位放电容量(ah / g)

VERSION = 'Epochs' # 수정

FILE_00 = 'data_csv/CYCLE_CSV_data00.csv'
FILE_01 = 'data_csv/CYCLE_CSV_data01.csv'
FILE_02 = 'data_csv/CYCLE_CSV_data02.csv'
FILE_03 = 'data_csv/CYCLE_CSV_data03.csv'
FILE_04 = 'data_csv/CYCLE_CSV_data04.csv'
FILE_05 = 'data_csv/CYCLE_CSV_data05.csv'
FILE_06 = 'data_csv/CYCLE_CSV_data06.csv'
    
RMSE_ = {}
MAE_ = {}
epoch_index = 0

 图2 电池数据

 图3 电池部分数据（有密集恐惧症的可自动忽略）

3.将上述数据分配至x、y坐标，分配至x坐标的有序号、cycle、累计容量、累计能源、库仑效率、能量效率、最大电压、最终充电电压、单位充电容量、放电最终电压、单位放电容量。

y坐标为：序号、cycle、充电号码容量、累计容量、能源、充电放电能源、累计_能源、库仑效率、能源效率、最大电压、最终电压、充电放电最终电压、单位充电容量、放电最终电压、单位放电容量。

第三行就是参数的设置：如窗口数设置为3，迭代次数设置为1000次，

接着就是使用try except语句来检测一段代码是否出现的异常并将异常信号进行输出。

drop_labels_x = ['序号', 'cycle', '累计_容量(ah)', '累计_能源(wh)', '库仑_ _效率(%)', '能源效率(%)', '最大_电压(v)', '最终充电电压(v)', '单位_ _充电容量(ah / g)', '放电最终电压(v)', '单位_ _放电容量(ah / g)']
drop_labels_y = [‘序号”、“cycle”、“充电_ _号码容量(ah)”、“累计_容量(ah)”、“_能源(wh)”、“充电放电_能源(wh)”、“累计_能源(wh)”、“库仑_ _效率(%)”、“能源效率(%)”、“最大_电压(v)”、“_最终电压(v)”、“充电放电_最终电压(v)”、“单位_ _充电容量(ah / g)”、“放电最终电压(v)”、“单位_ _放电容量(ah / g)”]

param = {'seq_len' : 20, 'num_units' : 32, 'num_filters' : 128, 'window' : 3, 'dropout': 0.2, 'num_epochs' : 1000, 'num_dense': 16}

log_dir = f"logs/{VERSION}/" + datetime.datetime.now().strftime("%Y%m%d-%H%M") + f'-{param["num_filters"]}FL-{param["num_units"]}UN-{param["num_epochs"]}EP-{param["seq_len"]}SQ'
file_path = f'Checkpoints\{VERSION}\SOH_Checkpoint\{param["num_filters"]}FL-{param["num_units"]}UN-{param["num_epochs"]}EP-{param["seq_len"]}SQ\{datetime.datetime.now().strftime("%Y%m%d-%H%M%S")}.h5'
hist_freq = 250

save_path = f'outputs\{VERSION}\{param["num_filters"]}FL-{param["num_units"]}UN-{param["num_epochs"]}EP-{param["seq_len"]}SQ'
try:
    if not os.path.exists(save_path):
        os.makedirs(save_path)
except OSError:
    print('Error Creating Directory...')

4.使用get_data函数来读取csv数据，并返回数据(最多2D)和data_y (1D)，数据正则化0~1。相当于MATLAB的plot函数。绘图结果如图4所示。

data00, data_cap00 = get_data(FILE_00, drop_labels_x, drop_labels_y)
# data01, data_cap01 = get_data(FILE_01, drop_labels_x, drop_labels_y)
data02, data_cap02 = get_data(FILE_02, drop_labels_x, drop_labels_y)
data04, data_cap04 = get_data(FILE_05, drop_labels_x, drop_labels_y)
data_test, data_cap_test = get_data(FILE_04, drop_labels_x, drop_labels_y)

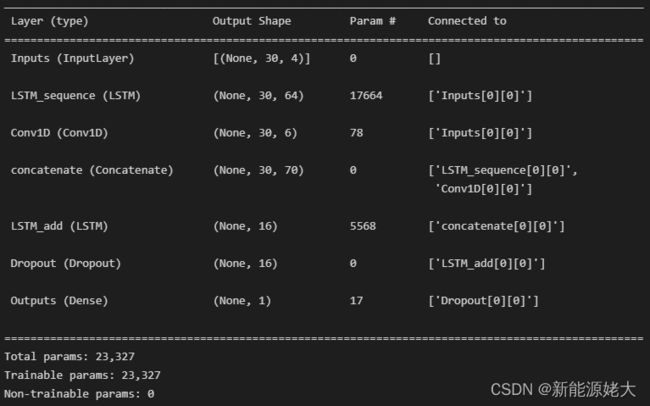
 5.使用LSTM神经网络进行训练数据的代码如下：训练的一些参数如图5所示：

x_train00 = seq_gen_x(data00, param['seq_len'])
y_train00 = seq_gen_y(data_cap00, param['seq_len'])
# x_train01 = seq_gen_x(data01, param['seq_len'])
# y_train01 = seq_gen_y(data_cap01, param['seq_len'])
x_train02 = seq_gen_x(data02, param['seq_len'])
y_train02 = seq_gen_y(data_cap02, param['seq_len'])
x_train04 = seq_gen_x(data04, param['seq_len'])
y_train04 = seq_gen_y(data_cap04, param['seq_len'])
x_test = seq_gen_x(data_test, param['seq_len'])
y_test = seq_gen_y(data_cap_test, param['seq_len'])
print(x_train00.shape)
print(y_train00.shape)
# print(x_train00[0:5, :, 1])
# print(y_train00[:4])
inputs = layers.Input(shape=(param['seq_len'], x_train00.shape[-1]), name = 'Inputs')
x1 = layers.Conv1D(param['num_filters'], param['window'], padding='causal', name = 'Conv1D')(inputs)
x2 = layers.LSTM(param['num_units'], return_sequences = True, name = 'LSTM_sequence')(inputs)
x = layers.concatenate([x2, x1])
x = layers.LSTM(16, name = 'LSTM_add')(x)
x = layers.Dropout(param['dropout'], name = 'Dropout')(x)
outputs = layers.Dense(1, name = 'Outputs')(x)
model = models.Model(inputs = inputs, outputs = outputs, name = 'CNN_LSTM_PARALLEL')
model.compile(loss = 'mse', optimizer = 'Adam')
model.summary()
BATCH_SIZE = 128
callback_list = [ModelCheckpoint(filepath = file_path, monitor = 'val_loss', save_best_only = True),
                 TensorBoard(log_dir=log_dir, histogram_freq=hist_freq)]
fitdata = model.fit(x_train00, y_train00, epochs=param['num_epochs'], verbose = 2, batch_size=BATCH_SIZE, validation_split=0.2, callbacks=callback_list)
# callback_list = [ModelCheckpoint(filepath = file_path, monitor = 'val_loss', save_best_only = True),
#                  TensorBoard(log_dir=log_dir, histogram_freq=hist_freq)]
# fitdata = model.fit(x_train01, y_train01, epochs=param['num_epochs'], verbose = 2, batch_size=BATCH_SIZE, validation_split=0.2, callbacks=callback_list)
callback_list = [ModelCheckpoint(filepath = file_path, monitor = 'val_loss', save_best_only = True),
                 TensorBoard(log_dir=log_dir, histogram_freq=hist_freq)]
fitdata = model.fit(x_train02, y_train02, epochs=param['num_epochs'], verbose = 2, batch_size=BATCH_SIZE, validation_split=0.2, callbacks=callback_list)
callback_list = [ModelCheckpoint(filepath = file_path, monitor = 'val_loss', save_best_only = True),
                 TensorBoard(log_dir=log_dir, histogram_freq=hist_freq)]
fitdata = model.fit(x_train04, y_train04, epochs=param['num_epochs'], verbose = 2, batch_size=BATCH_SIZE, validation_split=0.2, callbacks=callback_list)

 图5

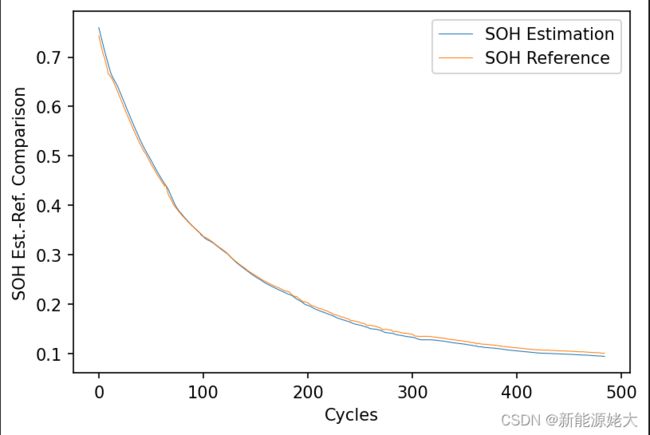
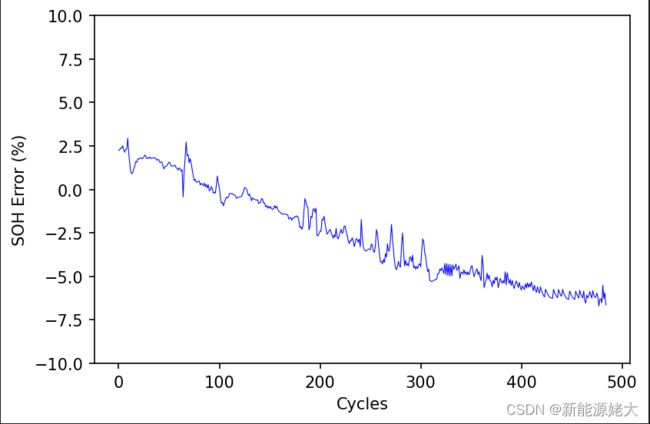
6.结果及绘图：最后的训练对比图如图7所示，训练的误差如图8所示：

pl.figure(dpi=150)
line = pl.plot(Error_rate)
pl.ylim(-10, 10)
pl.ylabel('SOH Error (%)')
pl.xlabel('Cycles')
pl.setp(line, color='b', linewidth=0.5)
pl.savefig(f'{output_path}\\ErrRate-RMSE({RMSE:.4f})MAE({MAE:.4f}).png')
pl.show()
print(f'RMSE({RMSE:.6f}), MAE({MAE:.6f})')

图7 LSTM预测SOH对比

图8 LSTM神经网络预测误差 

 预测的结果：RMSE=0.006097，MAE=0.05406

硕博期间所有的程序代码，一共2个多g，可以给你指导，赠送半个小时的语音电话答疑。电池数据+辨识程序+各种卡尔曼滤波算法都在里面了，后续还会有新模型的更新。快速入门BMS软件。某鹅：2629471989