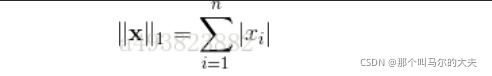整理五种相似性和相异性的度量方法
1、首先,先了解相似性和相异度的概念:
相似度:两个对象之间相似程度的数值度量,取值范围为0到1。
相异度:两个对象之间差异程度的数值度量,通常用“距离”衡量。
2、标称属性(含二元属性)相似度和相异度:
标称属性可以取2个或多个状态。假设一个标称属性的状态数目为M,则标称数据对象i和标称数据对象j之间的相异性可以根据不匹配率来计算。
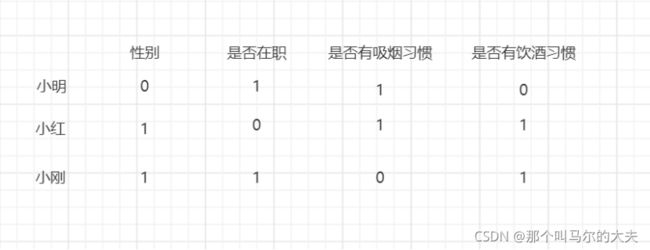
示例:
若将小明作为标称数据对象i,小刚作为标称数据对象j,计算两者的相异性与相似性。
按二元属性绘制列联表,结果如下:
| 小明 |
||||
| 小 刚 |
1 |
0 |
sum |
|
| 1 |
1(q) |
2(r) |
3(q+r) |
|
| 0 |
1(s) |
0(t) |
1(s+t) |
|
| sum |
2(q+s) |
2(r+t) |
4(p) |
|
其中,q是对象i和对象j都取1的属性数,t是在对象i中取1、对象j中取0的属性数,s是在对象i中取0、对象j中取1的属性数,而t是对象i和对象j都取0的属性数。属性的总数是p,其中p=q+r+s+t。
所以,当所有二元属性都看做具有相同权重的二元属性时,其相异性公式为:
d(i,j)= (r+s)/(q+r+s+t)=(2+1)/(1+2+1+0)=3/4
即状态不相同的属性数占所有属性数的比。
同样的,多元属性中,相异性公式也是如此。
相似性公式:sim(i,j)=1-d(i,j)。即状态相同的属性数占所有属性数的比
特殊地,对于非对称的二元属性,即两个状态不是同等重要的(如阴性阳性,人们往往更侧重于阳性的值)则计算相异性与相似性中,忽略掉t(负匹配数)。
相异性计算公式为:d(i,j)= (r+s)/(q+r+s)
相似性计算公式为:sim(i,j)=q/(q+r+s)=1-d(i,j)
3、数值属性相似性和相异性的度量:
(1)欧氏距离
欧式距离是高维空间中两点之间的距离,它计算简单、应用广泛,但是没有考虑变量之间的相关性,当体现单一特征的多个变量参与计算时会影响结果的准确性,同时它对向量中得每个分量的误差都同等对待,一定程度上放大了较大变量误差在距离测度中的作用。
两个n维向量A(x11,x12,…,x1n)与B(x21,x22,…,x2n)间的欧氏距离定义为:
D(A,B)=[(x11-x21)^2+(x12-x22)^2+…+(x1n-x2n)^2]^0.5
即将n组中计算每两个点距离的平方和再开方。
例如令数值属性对象i=(xi1,xi2,…,xip)和j=(xj1,xj2,…,xjp)具有p个数值属性的刻画,则对象i和j的欧式距离为:
D(i,j)=[(xi1-xj1)^2+(xi2-xj2)^2+…+(xip-xjp)^2]^0.5
对应L2范数
(2)曼哈顿距离
两个n维向量A(x11,x12,…,x1n)与B(x21,x22,…,x2n)间的曼哈顿距离定义为:
D(A,B)=|x11-x21|+|x12-x22|+…+|x1n-x2n|
对象i和j的曼哈顿距离为:
D(i,j)=|xi1-xj1|+|xi2-xj2|+…+|xip-xjp|
该距离又称L1范数,绝对误差和
(3)切比雪夫距离
两个n维向量A(x11,x12,…,x1n)与B(x21,x22,…,x2n)间的切比雪夫距离定义为:
D(A,B)=max{|x11-x21|,|x12-x22|,…,|x1n-x2n|}
对象i和j的切比雪夫距离为:
D(i,j)= max{|xi1-xj1|,|xi2-xj2|,…,|xip-xjp|}
(4)闵氏距离
对象i和j的闵氏距离为:
D(i,j)=[|xi1-xj1|^h+|xi2-xj2|^h+…+|xin-xjn|^h]^(1/h)
其中,h是实数,h≥1,这种距离又称Lp范数,即
p是一个可变参数。
当p=1时,就是曼哈顿距离,
当p=2时,就是欧氏距离,
当p→∞时,就是切比雪夫距离
(5)皮尔逊相关系数
皮尔逊相关系数也称为简单相关系数,它是衡量随机变量X与Y相关程度的一种方法,相关系数的取值范围是[-1,1]。相关系数的绝对值越大,则表明X与Y相关度越高,负值表示负相关,正值表示正相关。
令xi_bar、xj_bar分别为i和j向量各自的平均值。
则对象i和j的皮尔逊相关系数为:
r(i,j)=cov(i,j)/[(D(i)^0.5)*(D(j)^0.5)]=E((i-Ei)*(j-Ej))/ [(D(i)^0.5)*(D(j)^0.5)]
=[(xi1-xi_bar)(xj1-xjbar)+(xi2-xi_bar)(xj2-xj_bar)+…+(Xip-xibar)(xjp-xj_bar)]/{[(xi1-xi_bar)^2+(xi2-xi_bar)^2+…(xip-xi_bar)]*[(xj1-xj_bar)^2+(xj2-xj_bar)^2+…(xjn-xj_bar)]}^0.5。