Seq2Seq 模型详解

在NLP任务中，我们通常会遇到不定长的语言序列，比如机器翻译任务中，输入可能是一段不定长的英文文本，输出可能是不定长的中文或者法语序列。当遇到输入和输出都是不定长的序列时，可以使用编码器-解码器（encoder-decoder）模型或者seq2seq模型。其基本思想是编码器用来分析输入序列，解码器用来生成输出序列。

首先，来简单介绍下RNN（循环神经网络）结构：

1. RNN 结构

RNN结构

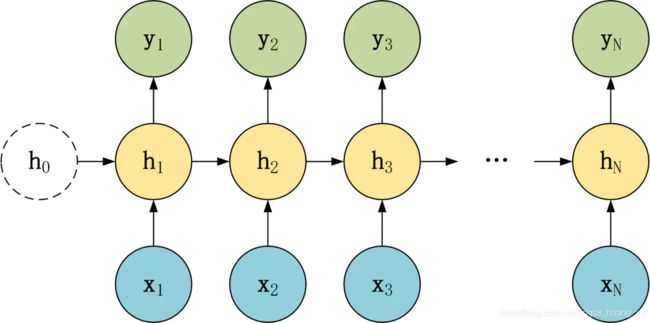
RNN中，每个单元接受两个输入，一个是当前时间步输入的信息 $X_t$，另一个是上一个单元的隐藏层状态 $H_{t-1}$。为什么这种结构的RNN适合用于做文本等序列型数据的任务，主要是因为隐藏状态的存在使得模型具有记忆性。针对不同的任务，根据输入和输出的数量，通常对RNN结构进行调整。

1. N to N
   该模型处理的一般是输入和输出序列长度相等的任务，如

   • 词性标注
   • 语言模型（Language Modeling）
     

2. 1 to N
   此类结构的输入长度为1，输出长度为N，一般又可以分为两种：一种是将输入只输入到第一个神经元，另一种将输入输入到所有神经元。

   一般用于以下任务：

   • 图像生成文字，一般输入 X 为图片，输出为一段图片描述性的文字；
   • 输入音乐类别，生成对应的音乐
   • 根据小说（新闻情感）类别，生成对应的文字
     
     

3. N to 1
   和1 to N相反，一般常见任务有：

   • 序列分类任务，如给定一段文本或语音序列，归类（情感分类，主题分类等）
     

2. Seq2Seq 模型

经过上面对几种RNN结构的分析，不难发现RNN结构大多对序列的长度比较局限，对于类似于机器翻译的任务，输入和输出长度并不对等，为N to M的结构，简单的RNN束手无策，因此便有了新的模型，Encoder-Decoder模型，也就是Seq2Seq模型。

模型一般由两部分组成：第一部分是Encoder部分，用于对输入的N长度的序列进行表征；第二部分是Decoder部分，用于将Encoder提取出的表征建立起到输出的M长度序列的映射。

1. 编码器 Decoder

Encoder部分一般使用了普通RNN的结构。其将一个序列表征为一个定长的上下文向量c，计算方式有多种，如下：

• $c=h_N$
• $c=f(h_N)$
• $c=f(h_1,h_2,\cdots ,h_N)$

2. 解码器 Decoder

相对于编码器而言，解码器的结构更多，下面介绍三种：

第一种

这种结构直接将Decoder得到的上下文向量作为RNN的初始隐藏状态输入到RNN结构中，后续单元不接受 c 的输入，计算公式如下：

• 隐藏状态的更新：
  $$\begin{gathered} {\mathbf{h}}_1^{\prime }=\sigma (\mathbf{W}\mathbf{c}+{\mathbf{b}}_1) \\ {\mathbf{h}}_{\mathbf{t}}^{\prime }=\sigma (\mathbf{W}{\mathbf{h}}_{\mathbf{t}-1}^{\prime }+{\mathbf{b}}_1) \end{gathered}$$
• 输出的计算：${\mathbf{y}}_{\mathbf{t}}^{\prime }=\sigma (\mathbf{V}{\mathbf{h}}_{\mathbf{t}}^{\prime }+{\mathbf{b}}_2)$

第二种

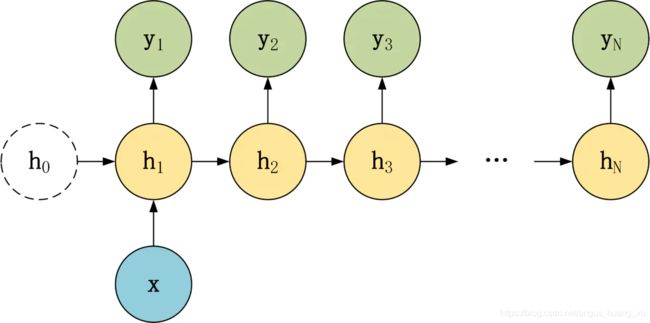
第二种将Encoder得到的上下文向量作为每个神经单元的输入，不再是只作为第一个单元的初始隐藏状态。计算公式如下：

• 隐藏状态：${\mathbf{h}}_{\mathbf{t}}^{\prime }=\sigma (\mathbf{U}\mathbf{c}+\mathbf{W}{\mathbf{h}}_{\mathbf{t}-1}^{\prime }+{\mathbf{b}}_1)$
• 输出：${\mathbf{y}}_{\mathbf{t}}^{\prime }=\sigma (\mathbf{V}{\mathbf{h}}^{\prime }\mathbf{t}+{\mathbf{b}}_2)$

第三种

第三种在 c 的处理上和第二种类似，但是区别在于将前一个神经单元的输出作为当前神经单元的输出。计算公式如下：

• 隐藏状态：${\mathbf{h}}_{\mathbf{t}}^{\prime }=\sigma (\mathbf{U}\mathbf{c}+\mathbf{W}{\mathbf{h}}_{\mathbf{t}-1}^{\prime }+\mathbf{V}{\mathbf{y}}_{\mathbf{t}-1}^{\prime }+{\mathbf{b}}_1)$
• 输出：${\mathbf{y}}_{\mathbf{t}}^{\prime }=\sigma (\mathbf{V}{\mathbf{h}}_{\mathbf{t}}^{\prime }+{\mathbf{b}}_2)$

3. Seq2Seq中的Trick

1. Teacher Forcing

主要针对第三种Decoder应用。当某一个单元输出出错时，如果将其输出传递给下一个单元，可能导致错误传递下去。这时候，需要在一定程度上减少这种传递，就采用按一定的比例决定是否对神经单元采用上一个上一个单元的输出作为输入。即：
$${\mathbf{h}}_{\mathbf{t}}^{\prime }=I(采用)\sigma (\mathbf{U}\mathbf{c}+\mathbf{W}{\mathbf{h}}_{\mathbf{t}-1}^{\prime }+\mathbf{V}{\mathbf{y}}_{\mathbf{t}-1}^{\prime }+{\mathbf{b}}_1)+I(不采用)\sigma (\mathbf{U}\mathbf{c}+\mathbf{W}{\mathbf{h}}_{\mathbf{t}-1}^{\prime }+{\mathbf{b}}_1)$$

2. Attention 机制（很重要）

提出Attention机制之前，我们先来看下之前的结构有什么问题：

核心问题是当序列过长时，上述的Decoder输出的上下文向量 c 无法记住所有信息，会出现长序列梯度消失的问题。比如句子有100个词，那么c里面可能丢失了前几个词的信息。

Attention 机制是怎样的？

Attention 机制其实是参考了人在翻译文章时候的注意力机制，它会将模型的注意力放在当前翻译的单词上，换句话说，它并不像前面提到的Encoder的结构一样对整个句子用一个表征，它对于每个单词都有一个以单词为中心的表征。Decoder结构如下：

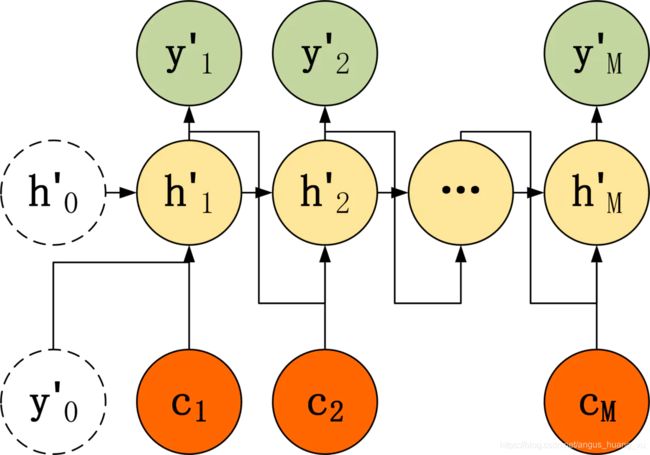
Encoder结构还是基本的RNN结构，需要保存每个神经元的隐藏状态 $h_t$。每个神经元依旧保持有隐藏状态$h_t$，但是上下文向量$c_i$的计算如下：

• 首先计算上一个神经元隐藏状态$h_{t-1}$与Encoder每一个神经元隐藏状态的相似度，用 $e_t$表示。$e_t=[a(h_{t-1}^{\prime },h_1),\cdots ,a(h_{t-1}^{\prime },h_N)]$，其中$a(\cdot )$为某种相似度计算函数。
• “集中注意力”。对以上$e_t$使用softmax函数，得到Encoder每个隐藏状态在处理第 t 个词的时候的“注意力” ${\alpha }_t$。计算得到各个上下文向量：$c_t={\sum }_{i=1}^N{\alpha }_{ti}{h}_i$
• 后面Decoder对 y 的计算与上面提到的第三种Decoder的计算方式几乎一致，区别就在于上下文向量 c 的变化。

3. 束搜索（Beam Search）

注意：Beam Search只用于测试，不用于训练过程。
当模型训练好后，给其输入一段话，其输出的每个单元的 y 给的是各个词的概率，我们如何根据概率选词且如何判断是否句子终止呢？

采取的方法是在每个时间步，选取当前时间步条件概率最大的k个词，作为该时间步的候选输出序列。如下图，k选择2，第一步p(A|c)和p(C|c)最大；第二步 P(AB|c),P(CE|c)最大；第三步P(ABD|c),P(CED|c)最大。

这样，得到的最终候选序列就是各个时间步的得到的序列的集合，下图种即为6个 {A, C, AB, CE, ABD, CED}。那么最终预测结果就是要从这6个中选出分最高的。这时候，可能有小伙伴会发现，那按概率算的话，序列越长的概率肯定越小呀，所以一般最后分数计算会有一个和序列长度有关的惩罚系数，如下：
$$\frac{1}{L^{\alpha }}\log P(y_1,y_2,\cdots ,y_L)=\frac{1}{L^{\alpha }}\sum _{t^{\prime }=1}^L\log P(y_{t^{\prime }}|y_1,\cdots ,y_{t^{\prime }-1},c)$$

其中L为候选序列的长度，$\alpha$ 一般选0.75. 这样一来，序列长的对应的系数更小，而由于取了对数，概率的对数是负数，如此变化后会使得长序列和短序列处于一个可比的情形。