【数据结构每日一题】队列——用栈实现队列

[数据结构习题]队列——用栈实现队列

知识点导航：【数据结构】栈和队列

[王道数据结构]习题导航：$page85.3$

本节为栈和队列的综合练习题

---

题目描述：

思路：双栈模拟

思路分析：

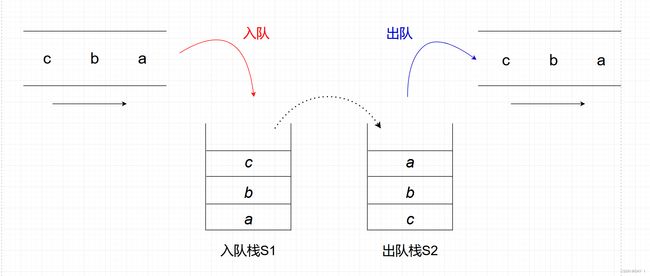
由于队列是先进先出的，而栈先进后出，所以需要定义两个栈来实现先进先出：先进$S1$ $\to$ 后出$S1$ $\to$ 后进$S2$ $\to$ 先出$S2$

step:

算法思路：利用栈$S1$与$S2$来模拟一个队列，当需要入队时，用$S1$来存放已入队的元素，则压入$S1$的栈顶；出队时，则将$S2$的栈顶元素出栈

1.实现栈的基本操作

①定义结构体 $+$ 初始化

由于为顺序栈，初始化即让 S.top==-1

#define Maxsize 50

typedef struct SqStack {
	int data[Maxsize];
	int top;
}SqStack;

//1.初始化
void InitStack(SqStack& S) {
	S.top = -1;
}

②判空&判满

对于顺序栈来说，判空为：S.top==-1 ；判满为：S.top==Maxsize-1

// 2.判满
bool Stackoverflow(SqStack& S) {
	if (S.top == Maxsize-1)
		return true;
	return false;
}

// 3.判空
bool Stackempty(SqStack& S) {
	if (S.top == -1)
		return true;
	return false;
}

③入栈

压入栈时，要判断栈是否已满，再让：S.data[++S.top]=x;

// 4.入栈
bool Push(SqStack& S, int x) {
	if (Stackoverflow(S))
		return false;
	S.data[++S.top] = x;
	return true;
}

④出栈

出栈时，先判断栈是否为空，再让：x=S.data[S.top--];

// 5.出栈
bool Pop(SqStack& S, int& x) {
	if (Stackempty(S))
		return false;
	x = S.data[S.top--];
	return true;
}

2.用栈实现队列操作

1.入队算法：

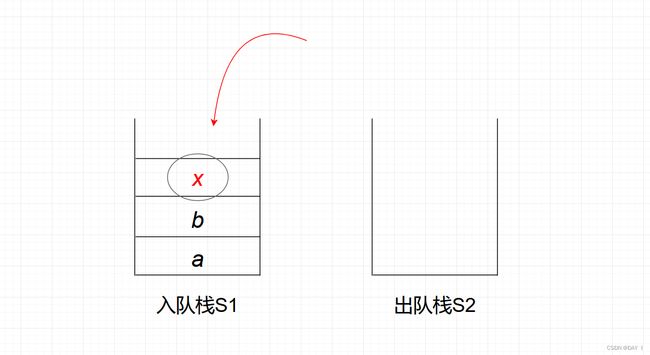
$x$入队时，是对入队栈 $S1$ 进行进栈操作，会出现几种情况：

①如果$S1$不为栈满状态，则直接将$x$压入$S1$中：

②如果$S1$栈满，而$S2$栈为空，则先将$S1$中的所有元素压入栈$S2$中，再将$x$压入S1中：

相当于先将输入的内容放入输出缓存区，这时候清空了输入条，则又可以继续输入了

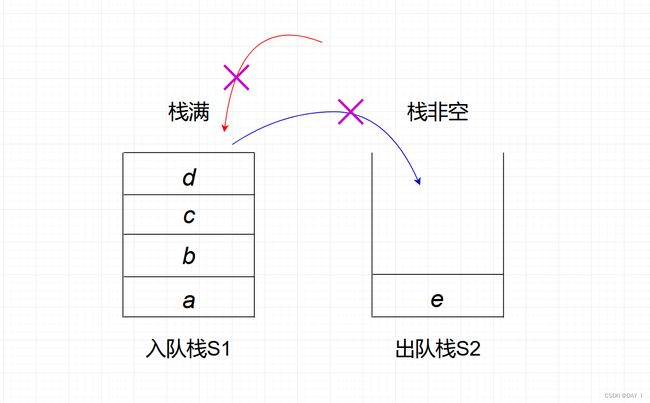
③如果$S1$栈满，而$S2$栈为非空状态，则入队失败：

同时这也意味着此时 队满：Stackoverflow(S1) && !Stackempty(S2)

哪也去不了！

入队代码实现：

// 6.入队
bool Enqueue(SqStack& S1, SqStack& S2, int x) {
	if (!Stackempty(S1)) { //如果S1不满 直接放到S1中
		Push(S1, x);
		return true;
	}
	else if (Stackoverflow(S1) && Stackempty(S2)) { //②如果S1满 而S2为空
		while (!Stackempty(S1)) { //将S1中所有元素压入S2中，再将x压入S1中
			int tmp;
			Pop(S1, tmp);
			Push(S2, tmp);
		}
		Push(S1, x);
		return true;
	}
	else if (Stackoverflow(S1) && Stackempty(S2)) { //如果S1满且S2不为空 则无法入队
		cout << "队列已满！" << endl;
		return false;
	}
}

2.出队算法：

由于从栈中取出元素是逆序的，所以必须先将$S1$中的所有元素依次出栈并压入$S2$中，在$S2$中进行出栈操作，而对出队栈$S2$的情况进行讨论：

①如果$S2$不为栈空，则直接将$S2$的栈顶元素弹出：

②如果$S2$为栈空，而$S1$不为空，则将$S1$中所有元素出栈并压入栈$S2$中，再对$S2$进行出栈：

③如果$S1$和$S2$均为空栈：

则出队失败，并且这也意味着此时 队空: Stackempty(S1) && Stackempty(S2)

代码实现：

// 7.出队
bool Dequeue(SqStack& S1,SqStack& S2,int &x) {
	if (!Stackempty(S2)) { //如果S2不空
		Pop(S2, x);
		return true;
	}
	else if (!Stackempty(S1) && Stackempty(S2)) { //如果S2空但S1不空
		while (!Stackempty(S1)) {
			Pop(S1, x);
			Push(S2, x);
		}
		Pop(S2, x);
		return true;
	}
	else if (Stackempty(S1) && Stackempty(S2)) {
		cout << "队列已空！" << endl;
		return false;
	}
}

3.队空&队满：

由上述可知：

1. 队空： Stackempty(S1) && Stackempty(S2)
2. 队满：Stackoverflow(S1) && !Stackempty(S2)

代码实现：

// 8.队列的判空
bool QueueEmpty(SqStack& S1, SqStack& S2) {
	if (Stackempty(S1) && Stackempty(S2))
		return true;
	return false;
}

// 9.队满的判断
bool QueueOver(SqStack& S1, SqStack& S2) {
	if (Stackoverflow(S1) && !Stackempty(S2))
		return true;
	return false;
}

完整代码实现：

#include
#define Maxsize 50
using namespace std;

typedef struct SqStack {
	int data[Maxsize];
	int top;
}SqStack;

// 1.初始化
void InitStack(SqStack& S) {
	S.top = -1;
}

// 2.判满
bool Stackoverflow(SqStack& S) {
	if (S.top == Maxsize-1)
		return true;
	return false;
}

// 3.判空
bool Stackempty(SqStack& S) {
	if (S.top == -1)
		return true;
	return false;
}

// 4.入栈
bool Push(SqStack& S, int x) {
	if (Stackoverflow(S))
		return false;
	S.data[++S.top] = x;
	return true;
}

// 5.出栈
bool Pop(SqStack& S, int& x) {
	if (Stackempty(S))
		return false;
	x = S.data[S.top--];
	return true;
}

// 6.入队
bool Enqueue(SqStack& S1, SqStack& S2, int x) {
	if (!Stackempty(S1)) { //如果S1不满 直接放到S1中
		Push(S1, x);
		return true;
	}
	else if (Stackoverflow(S1) && Stackempty(S2)) { //②如果S1满 而S2为空
		while (!Stackempty(S1)) { //将S1中所有元素压入S2中，再将x压入S1中
			int tmp;
			Pop(S1, tmp);
			Push(S2, tmp);
		}
		Push(S1, x);
		return true;
	}
	else if (Stackoverflow(S1) && Stackempty(S2)) { //如果S1满且S2不为空 则无法入队
		cout << "队列已满！" << endl;
		return false;
	}
}

// 7.出队
bool Dequeue(SqStack& S1,SqStack& S2,int &x) {
	if (!Stackempty(S2)) { //如果S2不空
		Pop(S2, x);
		return true;
	}
	else if (!Stackempty(S1) && Stackempty(S2)) { //如果S2空但S1不空
		while (!Stackempty(S1)) {
			Pop(S1, x);
			Push(S2, x);
		}
		Pop(S2, x);
		return true;
	}
	else if (Stackempty(S1) && Stackempty(S2)) {
		cout << "队列已空！" << endl;
		return false;
	}
}

// 8.队列的判空
bool QueueEmpty(SqStack& S1, SqStack& S2) {
	if (Stackempty(S1) && Stackempty(S2))
		return true;
	return false;
}

// 9.队满的判断
bool QueueOver(SqStack& S1, SqStack& S2) {
	if (Stackoverflow(S1) && !Stackempty(S2))
		return true;
	return false;
}

int main() {
	SqStack S1;
	SqStack S2;
	InitStack(S1);
	InitStack(S2);

	//初始化队列元素
	cout<<"请输初始化队列元素：" << endl;
	int x;
	while(cin>>x){
		Push(S1, x);
		if (cin.get() == '\n')
			break;
	}

	//入队
	cout<<"向队列中添加一个元素：" << endl;
	cin >> x;
	Enqueue(S1, S2, x);

	//出队
	cout<<"请输入要出队的元素个数：" << endl;
	int n;
	cin >> n;
	cout << "出队元素依次为：" << endl;
	int a=0;
	for (int i = 0; i < n; i++) {
		if (Dequeue(S1, S2, a))
			cout << a << " ";
		else
			break;
	}cout << endl;

	system("pause");
	return 0;
}

输出结果：

---

 

这是一道栈和链表的综合练习题，不是很难，但有利于知识点的回顾~

如有错误，欢迎指正~！