【C语言】语言篇——数组和字符串

C站的小伙伴们，大家好呀！我最近在阅读学习刘汝佳老师的《算法竞赛入门经典》，今天将整理本书的第三章——数组和字符串的一些习题，本章习题较多，下选取部分习题进行练习总结，在这里和大家分享，一起进步呀！✊✊✊

逆序输出

读入一些整数，逆序输出到一行中。已知整数不超过100个。

#include 
#include 
int maxn[105];//若数组较长则将其设为全局变量
int main (void)
{
    int i=0,x,k;
    memset(maxn,0,sizeof(maxn));//将数组清零
    while((scanf("%d",&x))==1) 
        maxn[i++]=x;//先将x赋值给maxn[i]，之后i++
    for (k=i-1;k>=0;k--)
    printf("%d ",maxn[k]);
    return 0;   

}

scanf()函数返回值
scanf()函数返回的是成功输入的变量的个数，当输入结束时，scanf()函数无法再次读取x，将返回0。
如何告诉程序输入结束了呢？
是按Enter/空格/TAB键吗？我们会发现，按Enter/空格/TAB键，并没有反应，这是因为程序正在等待输入。
在Windows下，输入完毕后先按Enter键，再按Ctrl+Z键，最后再按Enter键。在Linux下，输入完毕后按Ctrl+D键即可结束输入。
大数组需要定义在函数体外的原因
大数组需要定义在函数体外的原因，全局变量在静态存储区内分配内存，而局部变量是在栈内分配内存空间的。C语言编写的程序会在运行期间创建一个堆栈段，用来保存函数的调用关系和局部变量。而在main函数内部定义大数组相当于在栈内需要一个很大的空间，会造成栈的溢出。
因此，当我们需要定义一个极大的数组时，最好在main 函数外部定义这个大数组。

开灯问题

有n盏灯，编号为1～n。第1个人把所有灯打开，第2个人按下所有编号为2的倍数的开关（这些灯将被关掉），第3个人按下所有编号为3的倍数的开关（其中关掉的灯将被打开，开着的灯将被关闭）依此类推。一共有k个人，问最后有哪些灯开着？输入n和k，输出开着的灯的编号。k≤n≤1000。

样例输入：
7 3
样例输出：
1 5 6 7

分析：用a[1],a[2],a[3]……a[n]表示编号为1，2，3……n的灯是否开着。

#include 
#include 
int a[1000];
int main (void)
{
    int n,k,i,j;
    scanf("%d%d",&n,&k);
    memset(a,0,sizeof(a));//数组清零
    //0和1表示开灯和关灯两种状态
    for(i=1;i<=k;i++)//人
        for (j=1;j<=n;j++)//灯
            if (j%i==0)
            {
                if (a[j]==0)
                a[j]=1;
                else
                a[j]=0;
            }
    for(i=1;i<=n;i++)
    if (a[i]==1)
    printf("%d ",i);
    printf("\n");
    return 0;
}

0表示灯关的状态，1表示灯开的状态。从第一个人开始，判断是否是1~n编号的倍数，如果是的话，改变灯的状态，即原来是1，变为0；原来是0，变为1。

回文字

输入一个字符串，判断它是否为回文串以及镜像串。输入字符串保证不含数字0。所谓回文串，就是反转以后和原串相同，如abba和madam。所有镜像串，就是左右镜像之后和原串相同，如2S和3AIAE。注意，并不是每个字符在镜像之后都能得到一个合法字符。在本题中，每个字符的镜像如图所示（空白项表示该字符镜像后不能得到一个合法字符）。

输入的每行包含一个字符串（保证只有上述字符。不含空白字符），判断它是否为回文
串和镜像串（共4种组合）。每组数据之后输出一个空行。
样例输入：

NOTAPALINDROME
ISAPALINILAPASI
2A3MEAS
ATOYOTA

样例输出：

NOTAPALINDROME – is not a palindrome.
ISAPALINILAPASI – is a regular palindrome.
2A3MEAS – is a mirrored string.
ATOYOTA – is a mirrored palindrome.
分析过程可以看这篇：【C语言】经典题目二
下面是代码实现：

#include
#include
int main (void)
{
    char s[128]={0};
    int i,j,k,n;
    int flagH=1,flagJ=1;
    const char a[80]="AEHIJLMOSTUVWXYZ12358";
    const char b[80]="A3HILJMO2TUVWXY51SEZ8";
    gets(s);
    n=strlen(s);
    //判断是否是回文串
    for(i=0,k=n-1;i<k;i++,k--)
    {
        if (s[i]!=s[k])
        {
            flagH=0;
            break;
        }
    }
    //判断是否是镜像串
    for(i=0,k=n-1;i<k;i++,j--)
    {
        for (j=0;s[j]!=0;j++)
        {
            if (s[i]==a[j])
            {
                if (s[k]!=b[j])
                {
                    flagJ=0;
                }
            }
        }
        if (flagJ==0) break;
    }

    //根据标志量判断
    if(flagH==1 && flagJ==1)
    printf("%s -- is a mirrored palindrome.",s);
    else if (flagH==1 &&flagJ==0)
    printf(" %s-- is a regular palindrome.",s);
    else if (flagH==0 && flagJ==1)
    printf("%s -- is a mirrored string.",s);
    else 
    printf("%s-- is not a palindrome.",s);
    return 0;
}

习题

得分(score)

给出一个由O和X组成的串（长度为1～80），统计得分。每个O的得分为目前连续出现
的O的个数，X的得分为0。例如，OOXXOXXOOO的得分为1+2+0+0+1+0+0+1+2+3。
分析：对键盘输入的长串的每个字符进行判断。设置总和tot=0，若是X，则tot不累加。若是O，则需要判断前面O字符连续出现的个数。

#include
int main (void)
{
    char a[80]={0};
    int tot=0,i,k;
    gets(a);
    for(i=0;a[i]!='\0';i++)
    {
        if (a[i]=='O')
        {
            tot+=1;
            for (k=i-1;k>=0;k--)
            {
                if (a[k]!='O') break;
                else tot+=1;
            }
        }
    }
    printf("%d\n",tot);
    return 0;
}

分子量(Molar Mass)

给出一种物质的分子式（不带括号），求分子量。本题中的分子式只包含4种原子，分
别为C, H, O, N，原子量分别为12.01, 1.008, 16.00, 14.01（单位：g/mol）。例如，C6H5OH的
分子量为94.108g/mol。

分析：对输入的分子式的每个元素进行循环，其中会有数字和’C’,‘H’,‘O’,'N’四个字母，而我们只对四个字母进行判断。若是的话，看其后的一位是否为数字，若是，需要此原子量×数字，若不是，只需加它本身就可以了。
这里需要解决的是，如果输入的字符数组a中的元素等于’C’或’H’或’O’或’N’，如何利用其对应的原子量？
这里用结构体解决比较方便。可以将’C‘与其原子量12.01进行“捆绑”，将’H‘与其原子量1.008进行“捆绑”，将’O‘与其原子量16.00进行“捆绑”，将’N‘与其原子量14.01进行捆绑。

#include
struct Molar
{
    char atom;
    double mass;
};
int main (void)
{
    char a[30]={0};
    int i,k;
    double tot=0;
    gets(a);
    struct Molar b[4]={'C',12.01,'H',1.008,'O',16.00,'N',14.01};
    for (i=0;a[i]!='\0';i++)//遍历输入的a字符数组
    {
        for (k=0;k<=3;k++)
        if(a[i]==b[k].atom)
        {
            if (a[i+1]>='1' && a[i+1]<='9')//判断字符其后一位是否为数字
            tot+=b[k].mass * (a[i+1]-'0');//注意分子式中的数字都是以字符型存入字符数组的
            else
            tot+=b[k].mass;
        }
    }
    printf("%lf \n",tot);
    return 0;
}

数数字（Digit Counting）

把前n（n≤10000）个整数顺次写在一起：123456789101112…数一数0～9各出现多少次（输出10个整数，分别是0，1，…，9出现的次数）。
分析：利用sprintf()函数将1~10000输出到字符数组中。存入完毕后，对字符数组进行遍历即可。

关于memset()函数
memset()函数初始化是以一个字节为单位的，也就是说，对字符数组才能初始化为任意值。
memset()函数可以很方便将字符数组全部数组全部初始化为某一个值，例如：

c char a[20]; memset(a,'\0',sizeof(a))
将字符数组亲空。

#include
#include
char a[100000];
int main (void)
{
    int k=0,i;
    int b[10]={0};//用于记录1~9出现的次数
    char x;//记从键盘读入的数字字符
    memset(a,'\0',sizeof(a));//将字符数组清零
    scanf("%s",a);

    //对数组a进行遍历
    for(k=0;a[k]!='\0';k++)
    b[a[k]-'0']++;

    //输出数组b
    for(k=0;k<=9;k++)
    printf("%d ",b[k]);
    return 0;
}

周期串 (Periodic Strings)

如果一个字符串可以由某个长度为k的字符串重复多次得到，则称该串以k为周期。例如，abcabcabcabc以3为周期（注意，它也以6和12为周期）。
输入一个长度不超过80的字符串，输出其最小周期。
分析：对于一个字符串，其周期一定是字符串长度的因子，因此只对因子判断即可。
如何判断是否是周期呢？例如3为一个周期，则一定满足a[0]=a[0+3],a[1]=a[1+3],a[2]=a[2+3];
但是要做判断的话，满足的如上条件是仅仅不够的。例如会出现abcabcdddabcabcddd这种情况。所以我们需要对整个字符串进行判断。

#include 
#include 
int main (void)
{
    int i,k,len,n;
    int flag;  //设置标志量
    char s[80];
    gets(s);
    len=strlen(s);  
    for(i=1;i<=len;i++)
    {
        if (len%i==0)  //判断是否是因子
        //若是，判断能否为周期
        {
            flag=1;
            for (k=0;k<i;k++)
            {
                for (n=1;n<=len/i-1;n++)
                {
                    if (s[k]!=s[k+n*i]) flag=0;                   
                }
            }

        }
        if (flag==1)
        {
            printf("%d\n",i);
            break;
        }
    }
    return 0;   
}

DNA序列（DNA Consensus String）

输入m个长度均为n的DNA序列，求一个DNA序列，到所有序列的总Hamming距离尽量
小。两个等长字符串的Hamming距离等于字符不同的位置个数，例如，ACGTGCGAHamming距离为2（左数第1, 4个字符不同）。

输入整数m和n（4≤m≤50, 4≤n≤1000），以及m个长度为n的DNA序列（只包含字母A，C，G，T），输出到m个序列的Hamming距离和最小的DNA序列和对应的距离。如有多
解，要求为字典序最小的解。例如，对于下面5个DNA序列，最优解为TAAGATAC。

TATGATAC
TAAGCTAC
AAAGATCC
TGAGATAC
TAAGATGT

后来发现的问题：都错题了！！！求一个DAN序列，这是重点！
我的问题是从输入的DAN序列中找DAN序列，使得到所有的序列的总Hanming距离最小。

如果把题目改成这样的基础版，下面是分析过程。

分析：
首先是要处理m个DAN序列的储存，我们可以利用二维数组进行存储（因为二维数组可以看作是很多个一维数组组成。）
其次是如何如何找出最优解。其实就是，第一个序列和剩下的所有的序列进行比较，然后出现不同的字符，……（这个和我们熟悉的选择排序是不一样的，因为选择排序是和它后面的每一个数字进行比较，而这个是和所有的进行比较。）
那么如何储存每个序列总Hamming距离呢？不妨可以放在一个数组中用来存放。
那么如何输出呢？我们需要边存储边记录，设置变量min，若在每一次的比较中，有总HAMMING距离小于min，那么将此赋值给min，并将此时的DAN序列拷贝到字符数组s中。最终输出s即可。

这里需要注意的是，题目要求如有多解，要求为字典序最小的解。所以我们可以试着从最后一个DAN序列开始循环。

#include
#include
int main(void)
{
    char a[50][1000];  //用来存储DAN序列，保证长度足够长
    char s[1000]; //用来存储最优DAN序列
    int b[50]={0}; //记录每个DAN序列的Hamming距离值
    int i=0,k,j;
    int m,n;//m行n列
    scanf("%d%d",&m,&n);
    int min=(m-1)*n; //min一定小于等于(m-1)*n 完成初始化

    for (i=0;i<m;i++)
    scanf("%s",&a[i]);//输入m个DAN序列

    for(k=m-1;k>=0;k--) //从最后一行开始
    {
        for(i=0;i<m;i++)
        {
            for(j=0;j<n;j++)
            {
                if (a[k][j]!=a[i][j])
                b[k]++;
            }
        }
        if(b[k]<=min)
        {
            min=b[k];
            strcpy(s,a[k]);
        }  
          
    }
    //输出
    //输出m个序列的Hamming值
    for (j=0;j<m;j++)
    printf("%d ",b[j]);
    printf("\n");
    //输出最小的DAN序列及对应的值
    printf("%s\n%d",s,min);
    
    return 0;   
}

运行结构如下：

思考

题目1（必要的存储量）：
数组可以用来保存很多数据，但在一些情况下，并不需要把数据保存下来。下面哪些题目可以不借助数组，哪些必须借助数组？请编程实现。假设输入只能读一遍。

1. 输入一些数，统计个数。
2. 输入一些数，求最大值、最小值和平均数。
3. 输入一些数，哪两个数最接近。
4. 输入一些数，求第二大的值。
5. 输入一些数，求它们的方差。

1，输入一些数，统计个数。
显然不需要将数据存入数组中，我们只需要设置一个变量作为累加器即可。
如下：

#include   int main (void) {
    int count=0;
    double x;
    while (scanf("%lf",x)==1)
    count++;
    printf("%d\n",count);  } 
   

2，输入一些数，求最大值、最小值和平均数。

第二个可以利用数组实现，但也可以在循环中实现。

定义变量max，和min用来存放最大值和最小值。假设第一个输入的数字既是最大值也是最小值（即先完成初始化），然后后面每输入一个数，都和最大值和最小值比较，若比最大值大，则将此数赋值给max，对于min同理。

那么如何求平均值呢？可以定义和变量sum，每输入一个数，就将此数加到sum中，然后最后sum除以输入的数的总数即可。

#include 
int main (void)  
{
    int count=1;
    double max,min,sum,x,ave;
    scanf("%lf",&x);
    min=max=x;
    sum=x;
    while(scanf("%lf",&x)==1)
    {
        count+=1;
        if (x>=max)
        {
            max=x;
        }
        if (x<=min)
        {
            min=x;
        }
        sum+=x;
    }
    ave=sum/count;
    printf("max=%.2lf,min=%.2lf,average=%.2lf\n",max,min,ave);
    return 0;   
} 

3,输入一些数，哪两个数最接近。（假设输入的都是整数）

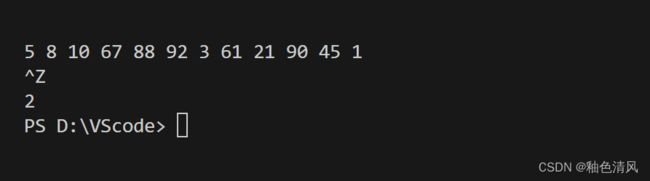
我的想法是，将输入的数字从小到大排序，然后相邻的两个数之间相减，即可，将差值放到变量min中。利用循环，依次判断两个数的差值，若小于min，将将此差值 赋值给min。

对于数字的排序，可以利用选择排序法和起泡排序法。

#include
#include  int maxn[10000];//保证数组足够大  int main (void)   {
    int k=0,i,x;//x用来存放每次输入的值
    int count=0;//累加器
    int tmp;//设置中间变量
    int min;//存放差值的最小值
    memset(maxn,0,sizeof(maxn));//数组初始化为0；

    //输入一些数字

    while(scanf("%d",&x)==1)
    {
        maxn[k++]=x;
        count++;
    }

    //输入完毕，对输入的数字排序
    //下采用选择法进行排序

    for(i=0;i<count;i++)
    {
        for (k=i+1;k<count;k++)
        {
            if (maxn[k]<maxn[i]) 
            //若后面的小于它，则利用中间变量交换
            {
                tmp=maxn[i];
                maxn[i]=maxn[k];
                maxn[k]=tmp;
            }

        }
    }
    min=maxn[1]-maxn[0];//初始化
    for(i=1;i<count-1;i++)
    {
        if(maxn[i+1]-maxn[i]<min)
        min=maxn[i+1]-maxn[i];
    }

    printf("%d\n",min);
    return 0; 
    } 
    

运行结果：

4.输入一些数，求第二大的值。
对于这个题目，可以只借助两个变量来实现。一个变量存放当前输入的整数中的最大值，一个变量存放当前输入的整数中的第二大值。

#include
int main(void)
{
    int maxF,maxS,x;
    scanf("d",&x);
    maxF=maxS=x;//初始化
    while(scanf("%d",&x)==1)
    {
        if(x>maxF)
        {
            maxS=maxF;  //易出错
            maxF=x;1
        }
        else if(x>maxS && x<maxF)
        maxS=x;
    }
    printf("%d\n",maxS);
    return 0;
}

5. 输入一些数，求它们的方差。
求方差，需要先求出来平均值。其次将各项与平均值作差并且平方相加，再除以总数。我们需要利用输入的每个数，所以需要利用数组，将数据保存。

#include 
#include 
int maxn[1000];//定义足够大的数组
int main (void)
{
    memset(maxn,0,sizeof(maxn));//数组初始化为0
    int x,sum=0,k=0,count=0,i;
    double ave,var=0;//平均值和方差

    //输入一些数
    while(scanf("%d",&x)==1)
    {
        maxn[k++]=x;
        sum+=x;
        count++;
    }
    //计算平均值
    ave=(double)sum/count;//注意强制转换sum
    //计算方差
    for (i=0;i<count;i++)
    {
        var+=(maxn[i]-ave)*(maxn[i]-ave);
    }
    var=var/count;
    
    printf("%.2lf",var);
    return 0;

}