python数据分析与挖掘实战(家用热水器用户行为分析与事件识别）

一、导言

居民在使用家用热水器的过程中，会因为地区气候、不同区域和用户年龄性别差异等原因形成不同的使用习惯。家用企业若能深入了解其产品在不同用户群的使用习惯，开发符合客户需求何时哦那个习惯的功能，就能开拓新市场。

本篇文章将依据BP神经网络算法构建洗浴事件识别模型，进而对不同地区的用户的洗浴事件进行识别，然后根据识别结果比较不同客户群提供最合适的个性化产品，改进新产品的智能化研发并制定相应的营销策略。

二、数据探索分析

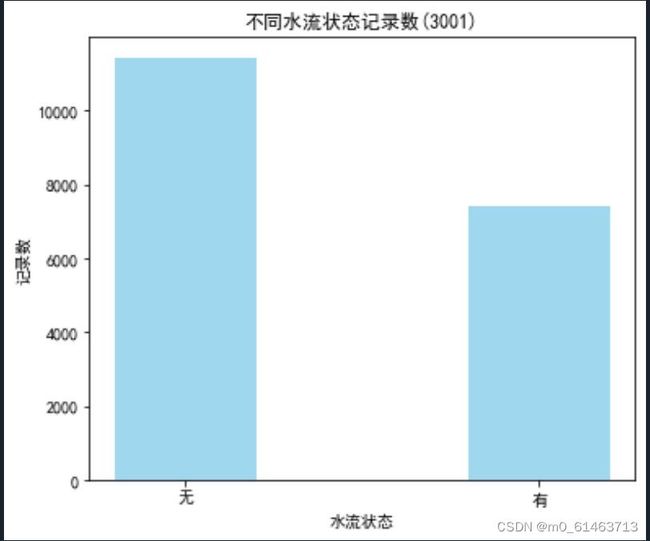
探索分析热水器的流量状况，其中“有无水流”和“水流量”属性最能直观体现热水器的水流量情况，对这两个属性进行探索分析。

import pandas as pd
import matplotlib.pyplot as plt

inputfile ='./data/original_data.xls' #'./original_data.xls'  # 输入的数据文件
data = pd.read_excel(inputfile)  # 读取数据

# 查看有无水流的分布
# 数据提取
lv_non = pd.value_counts(data['有无水流'])['无']
lv_move = pd.value_counts(data['有无水流'])['有']
# 绘制条形图
 
fig = plt.figure(figsize = (6 ,5))  # 设置画布大小
plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False
plt.bar([0,1], height=[lv_non,lv_move], width=0.4, alpha=0.8, color='skyblue')
plt.xticks([index for index in range(2)], ['无','有'])
plt.xlabel('水流状态')
plt.ylabel('记录数')
plt.title('不同水流状态记录数(3001)')
plt.show()
plt.close()

# 查看水流量分布
water = data['水流量']
# 绘制水流量分布箱型图
fig = plt.figure(figsize = (5 ,8))
plt.boxplot(water, 
            patch_artist=True,
            labels = ['水流量'],  # 设置x轴标题
            boxprops = {'facecolor':'lightblue'})  # 设置填充颜色
plt.title('水流量分布箱线图(3001)')
# 显示y坐标轴的底线
plt.grid(axis='y')
plt.show()

得到如下的条形图和箱型图

 

由此可知无水流状态的记录明显比有水流状态的记录要多。箱体贴近0，说明无水流量的记录较多，水流量的分布与水流量状态的分布一致。

三、数据预处理

3.1 属性归约

热水器采集的用水数据较多，针对分析的主要对象为热水器用户，因此将删除冗余属性，例：“热水器编号”“有无水流”“节能模式”。

import pandas as pd
import numpy as np
data = pd.read_excel('./data/original_data.xls')
print('初始状态的数据形状为：', data.shape)
# 删除热水器编号、有无水流、节能模式属性
data.drop(labels=["热水器编号","有无水流","节能模式"],axis=1,inplace=True) 
print('删除冗余属性后的数据形状为：', data.shape)
data.to_csv('./data/water_heart.csv',index=False)

结果如下

3.2 划分用水事件

热水器用户的用水数据储存在数据库中，记录了各种各样的用水事件，包括洗浴、洗手、刷牙、洗脸、洗衣、洗菜等，本案例要在大量的状态记录中划分出哪些连续的数据时一次完整的用水事件。用水时间划分主要分为两个步骤，即确定单次用水时长间隔，计算两条相邻记录的时间。

# 读取数据
data = pd.read_csv('./data/water_heart.csv')
# 划分用水事件
threshold = pd.Timedelta('4 min')  # 阈值为4分钟
data['发生时间'] = pd.to_datetime(data['发生时间'], format = '%Y%m%d%H%M%S')  # 转换时间格式
data = data[data['水流量'] > 0]  # 只要流量大于0的记录
sjKs = data['发生时间'].diff() > threshold  # 相邻时间向前差分，比较是否大于阈值
sjKs.iloc[0] = True  # 令第一个时间为第一个用水事件的开始事件
sjJs = sjKs.iloc[1:]  # 向后差分的结果
sjJs = pd.concat([sjJs,pd.Series(True)])  # 令最后一个时间作为最后一个用水事件的结束时间
# 创建数据框，并定义用水事件序列
sj = pd.DataFrame(np.arange(1,sum(sjKs)+1),columns = ["事件序号"])
sj["事件起始编号"] = data.index[sjKs == 1]+1  # 定义用水事件的起始编号
sj["事件终止编号"] = data.index[sjJs == 1]+1  # 定义用水事件的终止编号
print('当阈值为4分钟的时候事件数目为：',sj.shape[0])
sj.to_csv('./data/sj.csv',index = False)

结果如下

3.3 确定单次用水事件时长阙值

对某热水器用户的数据，根据不同的阙值划分用水事件，得到相应的事件个数，阙值变化与划分得到时间个数。统计出各个阙值下的用水事件的个数，再通过阙值寻优的方式找到最优的阙值。

# 确定单次用水事件时长阈值
n = 4  # 使用以后四个点的平均斜率
threshold = pd.Timedelta(minutes=5)  # 专家阈值
data['发生时间'] = pd.to_datetime(data['发生时间'], format='%Y%m%d%H%M%S')
data = data[data['水流量'] > 0]  # 只要流量大于0的记录
# 自定义函数：输入划分时间的时间阈值，得到划分的事件数
def event_num(ts):
    d = data['发生时间'].diff() > ts  # 相邻时间作差分，比较是否大于阈值
    return d.sum() + 1  # 这样直接返回事件数
dt = [pd.Timedelta(minutes=i) for i in np.arange(1, 9, 0.25)]
h = pd.DataFrame(dt, columns=['阈值'])  # 转换数据框，定义阈值列
h['事件数'] = h['阈值'].apply(event_num)  # 计算每个阈值对应的事件数
h['斜率'] = h['事件数'].diff()/0.25  # 计算每两个相邻点对应的斜率
h['斜率指标']= h['斜率'].abs().rolling(4).mean()  # 往前取n个斜率绝对值平均作为斜率指标
ts = h['阈值'][h['斜率指标'].idxmin() - n]
# 用idxmin返回最小值的Index，由于rolling_mean()计算的是前n个斜率的绝对值平均
# 所以结果要进行平移（-n）
if ts > threshold:
    ts = pd.Timedelta(minutes=4)
print('计算出的单次用水时长的阈值为：',ts)

结果如下

 

3.4 属性构造 

1）构建用水时长与频率属性

不同用水事件的用水时长是基础属性之一。用水时长相关的属性只能区分出一部分用水事件，不同用水事件的用水停顿和频率也不同。构建用水时长与用水频率属性。

data = pd.read_csv('./data/water_heart.csv',encoding='utf-8')  # 读取热水器使用数据记录
sj = pd.read_csv('./data/sj.csv')  # 读取用水事件记录
# 转换时间格式
data["发生时间"] = pd.to_datetime(data["发生时间"],format="%Y%m%d%H%M%S")

# 构造特征：总用水时长
timeDel = pd.Timedelta("0.5 sec")
sj["事件开始时间"] = data.iloc[sj["事件起始编号"]-1,0].values- timeDel
sj["事件结束时间"] = data.iloc[sj["事件终止编号"]-1,0].values + timeDel
sj['洗浴时间点'] = [i.hour for i in sj["事件开始时间"]]
sj["总用水时长"] = np.int64(sj["事件结束时间"] - sj["事件开始时间"])/1000000000 + 1

# 构造用水停顿事件
# 构造特征“停顿开始时间”、“停顿结束时间”
# 停顿开始时间指从有水流到无水流，停顿结束时间指从无水流到有水流
for i in range(len(data)-1):
    if (data.loc[i,"水流量"] != 0) & (data.loc[i + 1,"水流量"] == 0) :
        data.loc[i + 1,"停顿开始时间"] = data.loc[i +1, "发生时间"] - timeDel
    if (data.loc[i,"水流量"] == 0) & (data.loc[i + 1,"水流量"] != 0) :
        data.loc[i,"停顿结束时间"] = data.loc[i , "发生时间"] + timeDel
        
# 提取停顿开始时间与结束时间所对应行号，放在数据框Stop中
indStopStart = data.index[data["停顿开始时间"].notnull()]+1
indStopEnd = data.index[data["停顿结束时间"].notnull()]+1
Stop = pd.DataFrame(data={"停顿开始编号":indStopStart[:-1],
                            "停顿结束编号":indStopEnd[1:]}) 
# 计算停顿时长，并放在数据框stop中，停顿时长=停顿结束时间-停顿结束时间
Stop["停顿时长"] = np.int64(data.loc[indStopEnd[1:]-1,"停顿结束时间"].values-
                     data.loc[indStopStart[:-1]-1,"停顿开始时间"].values)/1000000000
# 将每次停顿与事件匹配,停顿的开始时间要大于事件的开始时间，
# 且停顿的结束时间要小于事件的结束时间
for i in range(len(sj)):
    Stop.loc[(Stop["停顿开始编号"] > sj.loc[i,"事件起始编号"]) & 
           (Stop["停顿结束编号"] < sj.loc[i,"事件终止编号"]),"停顿归属事件"]=i+1
             
# 删除停顿次数为0的事件
Stop = Stop[Stop["停顿归属事件"].notnull()]

# 构造特征 用水事件停顿总时长、停顿次数、停顿平均时长、
# 用水时长，用水/总时长
stopAgg =  Stop.groupby("停顿归属事件").agg({"停顿时长":sum,"停顿开始编号":len})
sj.loc[stopAgg.index - 1,"总停顿时长"] = stopAgg.loc[:,"停顿时长"].values
sj.loc[stopAgg.index-1,"停顿次数"] = stopAgg.loc[:,"停顿开始编号"].values
sj.fillna(0,inplace=True)  # 对缺失值用0插补
stopNo0 = sj["停顿次数"] != 0  # 判断用水事件是否存在停顿
sj.loc[stopNo0,"平均停顿时长"] = sj.loc[stopNo0,"总停顿时长"]/sj.loc[stopNo0,"停顿次数"] 
sj.fillna(0,inplace=True)  # 对缺失值用0插补
sj["用水时长"] = sj["总用水时长"] - sj["总停顿时长"]  # 定义特征用水时长
sj["用水/总时长"] = sj["用水时长"] / sj["总用水时长"]  # 定义特征 用水/总时长
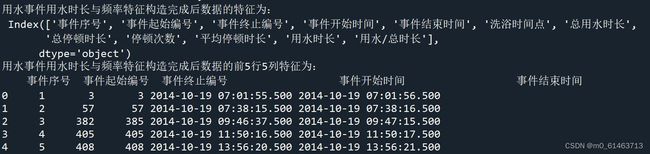
print('用水事件用水时长与频率特征构造完成后数据的特征为：\n',sj.columns)
print('用水事件用水时长与频率特征构造完成后数据的前5行5列特征为：\n',sj.iloc[:5,:5])

结果如下

2）构建用水量与波动属性

除了用水时长、停顿和频率外，用水量也是识别该事件是否为洗浴事件的重要属性。同时用水波动也是区分不同用水事件的关键。在用水时长和频率属性的基础之上构建用水量和用水波动属性。

data["水流量"] = data["水流量"] / 60 # 原单位L/min，现转换为L/sec
sj["总用水量"] = 0 # 给总用水量赋一个初始值0
for i in range(len(sj)):
    Start = sj.loc[i,"事件起始编号"]-1
    End = sj.loc[i,"事件终止编号"]-1
    if Start != End:
        for j in range(Start,End):
            if data.loc[j,"水流量"] != 0:
                sj.loc[i,"总用水量"] = (data.loc[j + 1,"发生时间"] - 
                                    data.loc[j,"发生时间"]).seconds* \
                                    data.loc[j,"水流量"] + sj.loc[i,"总用水量"]
        sj.loc[i,"总用水量"] = sj.loc[i,"总用水量"] + data.loc[End,"水流量"] * 2
    else:
        sj.loc[i,"总用水量"] = data.loc[Start,"水流量"] * 2
        
sj["平均水流量"] = sj["总用水量"] / sj["用水时长"] # 定义特征 平均水流量
# 构造特征：水流量波动
# 水流量波动=∑(((单次水流的值-平均水流量)^2)*持续时间)/用水时长
sj["水流量波动"] = 0 # 给水流量波动赋一个初始值0
for i in range(len(sj)):
    Start = sj.loc[i,"事件起始编号"] - 1
    End = sj.loc[i,"事件终止编号"] - 1
    for j in range(Start,End + 1):
        if data.loc[j,"水流量"] != 0:
            slbd = (data.loc[j,"水流量"] - sj.loc[i,"平均水流量"])**2
            slsj = (data.loc[j + 1,"发生时间"] - data.loc[j,"发生时间"]).seconds
            sj.loc[i,"水流量波动"] = slbd * slsj + sj.loc[i,"水流量波动"]
    sj.loc[i,"水流量波动"] = sj.loc[i,"水流量波动"] / sj.loc[i,"用水时长"]   

# 构造特征：停顿时长波动
# 停顿时长波动=∑(((单次停顿时长-平均停顿时长)^2)*持续时间)/总停顿时长
sj["停顿时长波动"] = 0 # 给停顿时长波动赋一个初始值0
for i in range(len(sj)):
    if sj.loc[i,"停顿次数"] > 1: # 当停顿次数为0或1时，停顿时长波动值为0，故排除
        for j in Stop.loc[Stop["停顿归属事件"] == (i+1),"停顿时长"].values:
            sj.loc[i,"停顿时长波动"] = ((j - sj.loc[i,"平均停顿时长"])**2) * j + \
                                     sj.loc[i,"停顿时长波动"]
        sj.loc[i,"停顿时长波动"] = sj.loc[i,"停顿时长波动"] / sj.loc[i,"总停顿时长"]

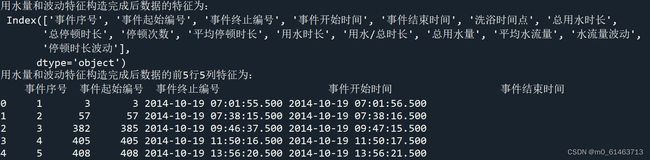
print('用水量和波动特征构造完成后数据的特征为：\n',sj.columns)
print('用水量和波动特征构造完成后数据的前5行5列特征为：\n',sj.iloc[:5,:5])

结果如下

 

 

3.5 筛选候选洗浴事件

洗浴事件的识别是建立在一次用水事件识别的基础上的，也就是从已经划分好的一次用水事件中识别出哪些一次用水事件是洗浴事件。基于构建的用水时长和用水量属性，筛选候选洗浴事件。

sj_bool = (sj['用水时长'] >100) & (sj['总用水时长'] > 120) & (sj['总用水量'] > 5)
sj_final = sj.loc[sj_bool,:]
sj_final.to_excel('./data/sj_final.xlsx',index=False)
print('筛选出候选洗浴事件前的数据形状为：',sj.shape)
print('筛选出候选洗浴事件后的数据形状为：',sj_final.shape)

结果如下

筛选前，用水事件数目总共为172个，经过筛选，余下75个用水事件。

四、模型构建

根据建模样本数据建立BP神经网络模型识别洗浴事件。构建BP神经网络模型需要注意数据本身属性之间存在的量级差异，因此需要进行标准化，消除量级差异。为了便于后续应用模型，可以用joblib.dump函数保存模型。

import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.neural_network import MLPClassifier
from sklearn.externals import joblib

# 读取数据
Xtrain = pd.read_excel('./data/sj_final.xlsx')
ytrain = pd.read_excel('./data/water_heater_log.xlsx')
test = pd.read_excel('./data/test_data.xlsx')
# 训练集测试集区分。
x_train, x_test, y_train, y_test = Xtrain.iloc[:,5:],test.iloc[:,4:-1],\
                                   ytrain.iloc[:,-1],test.iloc[:,-1]
# 标准化
stdScaler = StandardScaler().fit(x_train)
x_stdtrain = stdScaler.transform(x_train)
x_stdtest = stdScaler.transform(x_test)
# 建立模型
bpnn = MLPClassifier(hidden_layer_sizes = (17,10), max_iter = 200, solver = 'lbfgs',random_state=50)
bpnn.fit(x_stdtrain, y_train)
# 保存模型
joblib.dump(bpnn,'./data/water_heater_nnet.m')
print('构建的模型为：\n',bpnn)

结果如下

在训练BP神经网络时，对神经网络的参数进行了寻优，发现含有两个隐层的神经网络训练效果较好，其中两个隐层的隐节点数分别为17和10时训练的效果较好。

五、模型检验

结合模型评价的相关知识，使用精确率（precision）、召回率（recall）和F1值来衡量模型评价的效果较为客观、准确。同时结合ROC曲线，可以更加直观地评价模型的效果。

# 模型评价
from sklearn.metrics import classification_report
from sklearn.metrics import roc_curve
from sklearn.externals import joblib
import matplotlib.pyplot as plt

bpnn = joblib.load('./data/water_heater_nnet.m')  # 加载模型
y_pred = bpnn.predict(x_stdtest)  # 返回预测结果
print('神经网络预测结果评价报告：\n',classification_report(y_test,y_pred))
# 绘制roc曲线图
plt.rcParams['font.sans-serif'] = 'SimHei'  # 显示中文
plt.rcParams['axes.unicode_minus'] = False  # 显示负号
fpr, tpr, thresholds = roc_curve(y_pred,y_test)  # 求出TPR和FPR
plt.figure(figsize=(6,4))  # 创建画布
plt.plot(fpr,tpr)  # 绘制曲线
plt.title('用户用水事件识别ROC曲线(3001)')  # 标题
plt.xlabel('FPR')  # x轴标签
plt.ylabel('TPR')  # y轴标签
plt.savefig('./data/用户用水事件识别ROC曲线.png')  # 保存图片
plt.show()  # 显示图形

结果如下

 

 可得在洗浴事件识别上精确率（precision）非常高，高达90%，同时召回率（recall）也达到70%以上。因此可以确定此次创建的模型是有效且效果良好的，能够用于实际的洗浴事件的识别中。