禁忌搜索算法(tabu search)解决TSP及其Matlab代码

1、算法简介

禁忌搜索算法TS(Tabu search)，顾名思义核心在于“禁忌”，简单来说就是在某一个过程中把一些不太好的操作给禁止了，直到搜索到一个“最优秀”的。它是在1986年由美国Fred Glover教授提出的，主要是为了提高寻优过程中的全面搜索的能力。

 

 

禁忌搜索算法通过模拟人类智能的记忆特点，引入存储结构和相应的禁忌准则来避免迂回循环，通过特赦准则来释放禁忌表中较优的个体，进而保证多样性的搜索来尽可能达到问题的最优解。

2、算法核心概念

禁忌表(TabuList)：是用来存放禁忌对象的表。它是TS算法的核心，禁忌表的值在每一次迭代过程中都会完成一次更新。禁忌对象可以是TSP中的路径长度、城市顺序等等。

禁忌长度(TabuLength)：禁忌表中存放的数值即为禁忌长度，它规定了禁忌对象的生存时间，一旦达到其禁忌长度，则会被解除禁忌状态。禁忌长度的选取有静态和动态选取两种方法，静态选取会事先固定禁忌长度，而动态选取则会根据迭代过程而发生变化。

特赦准则：是在搜索过程中，发现有解比当前最优解更优时执行替换最优解的操作，或者在搜索过程中全部候选解都在“禁忌”状态，能够释放特定解的操作。

领域解：在初始解的基础上，按照一定的方向对初始解进行移动所形成的新解，称为领域解。不重复的移动次数称为领域的规模。

候选解：候选解就是领域解中较为优秀的一部分解。若候选解所选的规模较小，算法则会过早收敛，造成局部最优解的情况，若候选解所选规模较大，算法则会浪费较多的时间和空间来搜索最优解。

3、算法流程

禁忌搜索算法的一般流程如下：

（1）初始化TS算法的参数，按照准则生成问题的初始解，生成0禁忌表；

（2）判断是否满足终止条件，若是，则结束算法，输出结果

（3）根据算法的特性生成领域解，并从中选择合适规模大小的候选解；

（4）判断候选解中的最优解Next是否满足特赦准则，若满足特赦准则，则用Next替代当前最优解Before，并更新禁忌表，令Next对应的禁忌对象的禁忌长度为最长，即禁忌时间最长；若不满足特赦准则，进行（4）步骤；

（5）判断候选解中禁忌状态情况，找出候选解中处于“非禁忌”状态的禁忌对象，并把该禁忌对象对应的解赋给当前最优解，同时设置该禁忌对象的禁忌时间为最长；

（6）转（2）；

4、实例及Matlab代码

接下来，利用Tabu Search算法来解决TSP问题。假设有48个随机分布的城市如下图所示，一个旅行商从一个城市出发，遍历完所有城市，要求其旅行距离最短。在这一过程中，禁忌对象为互换城市对，就是在解中把两个城市的位置调换。

function TspTBout = TSPTabusearch(xy,dmat,TabuLength,IterNum,showProg,showResult)
%运用禁忌搜索算法解决TSP问题
nargs = 6;
%检查函数输入
for i = nargin:nargs-1 %nargin代表函数已输入参数个数
    switch i 
        case 0 %产生城市坐标
            xy =[488,814;1393,595;2735,2492;4788,4799;4825,1702;789,2927;4853,1120;4786,3757;2427,1276;4002,2530;710,3496;2109,4455;4579,4797;3962,2737;4798,694;3279,747;179,1288;4246,4204;4670,1272;3394,4072;3789,1218;3716,4647;
                1962,1750;3278,983;856,1256;3531,3081;160,2367;1385,1759;231,4155;486,2927;4118,2749;3475,4586;1586,1430;4752,3787;173,3769;2194,1903;1908,2840;3828,380;3976,270;935,2654;2449,3896;2228,4671;3232,650;3547,2845;3774,2347;1381,60;3399,1686;3276,811];
        case 1%计算距离矩阵
            N = size(xy,1);
            a =meshgrid(1:N);%生成N*N升序矩阵
            dmat = reshape(sqrt(sum((xy(a,:)-xy(a',:)).^2,2)),N,N);% '为矩阵的转置，reshape把数据生成N*N的矩阵
        case 2%设置禁忌长度（禁忌时间）
            TabuLength = round((N*(N-1)/2)^0.5);%round四舍五入
        case 3%设置迭代次数
            IterNum = 1e3;
        case 4%是否展示迭代过程
            showProg = 1;
        case 5%是否展示最终结果
            showResult = 1;
        otherwise
    end
end
%对输入参数进行检查
[N,~] = size(xy);%城市个数、维数
[nr,nc] = size(dmat);%距离矩阵的行数和列数
if N~=nr || N~=nc
    error('城市坐标或距离矩阵输入有误')
end
showProg = logical(showProg(1));%将数值转变为逻辑值
showResult = logical(showResult(1));
%画出城市位置分布图
figure(1);
plot (xy(:,1),xy(:,2),'k.');
title('城市坐标位置');

%% 禁忌搜索算法参数设置
TabuList = zeros(N);%禁忌表设置为城市互换对，为N*N的矩阵，矩阵中的值代表禁忌长度，初始禁忌长度为0
CandidatesNum = 200; %领域解的个数，由领域解选出候选解
Candidates = zeros(CandidatesNum,N);%领域解集合
S0 = randperm(N);%随机产生一个初始解
Broute = S0;%当前最佳的路劲
Bdist = Inf;%当前最佳路径总距离
BLHistory = zeros(IterNum,1);%记录最优路径长度

%% 禁忌搜索循坏
for iter = 1:IterNum
    %% 以下生成城市互换对矩阵Twocity[200,2]
    Twocity = zeros(CandidatesNum,2);
    i = 1;
    while i<= CandidatesNum
        M = ceil(N*rand(1,2));%随机生成两个城市序号
        if M(1) ~= M(2)
            Twocity(i,1) = max(M(1),M(2));%最小值存在1，最大值存在2
            Twocity(i,2) = min(M(1),M(2));
            if i ==1
                isa = 0;%是否生成相同的城市互换对，1为生成了
            else
                for j = 1:i-1
                    if Twocity(i,1)==Twocity(j,1)&&Twocity(i,2)==Twocity(j,2)
                        %若相同
                        isa =1;
                        break;
                    else
                        isa =0;
                    end
                end
            end
            if ~isa %若生成的城市对与之前的都不相同则可以继续生成城市对
                i =i+1;
            end
        end
    end
   %% 产生领域解，选取前100个为候选解 
     %保留前100个最好领域解为候选解
     BestCandNum = 100;
     %定义一个表格，四列，分别存储领域解序号i,路径长度L(i),Twocity(i,1),Twocity(i,2)
     BCandidate = Inf * ones(BestCandNum,4);
     L = zeros(1,CandidatesNum);
     %相当于产生一个S0的解，包含有200个领域解，从中找出最佳的100个才是候选解
     for i = 1:CandidatesNum
         Candidates(i,:) = S0;%领域解
         Candidates(i,[Twocity(i,2),Twocity(i,1)]) = S0([Twocity(i,1),Twocity(i,2)]);%在当前解S0上交换两个城市的位置
         %计算当前领域解路径的距离
         L(i) = CalDistofS(dmat,Candidates(i,:));
         
         %选出100个最好的领域解充当候选解
         if i<= BestCandNum
            BCandidate(i,1) = i;
            BCandidate(i,2) = L(i);
            BCandidate(i,3) = S0(Twocity(i,1));
            BCandidate(i,4) = S0(Twocity(i,2));
         else
             for j =1:BestCandNum
                if L(i) < BCandidate(j,2)%领域解超出100个，则需要比较选取较小距离的
                    BCandidate(j,1) = i;
                    BCandidate(j,2) = L(i);
                    BCandidate(j,3) = S0(Twocity(i,1));
                    BCandidate(j,4) = S0(Twocity(i,2));
                    break;
                end
             end
         end
     end
     %根据距离，对候选解进行排序
     [~,Index] = sort(BCandidate(:,2));%Index是BCandidate中距离升序排列后的索引
     SBest = BCandidate(Index,:);
     BCandidate = SBest;% 此时的BCandidate是按第二列路径长度升序排列的
     %% 特赦准则是否满足，更新禁忌表
     if BCandidate(1,2)< Bdist%如果小于当前最优
         Bdist = BCandidate(1,2);
         %当前最优解变为候选解中的第BCandidate（1,1）行
         S0 = Candidates(BCandidate(1,1),:);
         Broute = S0;
         for m = 1:N
             for n = 1:N
                 if TabuList(m,n) ~=0
                     TabuList(m,n) = TabuList(m,n) -1;%更新禁忌表，禁忌长度减1
                 end
             end
         end
         TabuList(BCandidate(1,3),BCandidate(1,4)) = TabuLength;%更新禁忌表
     else %若没有找到比当前最优解更好的解
         for i = 1:BestCandNum
             if TabuList(BCandidate(i,3),BCandidate(i,4)) == 0%如果已经解禁了
                 S0 = Candidates(BCandidate(i,1),:);
                 for m = 1:N
                     for n = 1:N
                         if TabuList(m,n) ~=0
                           TabuList(m,n) = TabuList(m,n) -1;%更新禁忌表，禁忌长度减1
                         end
                     end
                 end
                 TabuList(BCandidate(i,3),BCandidate(i,4)) = TabuLength;%更新禁忌表
                 break;
             end
         end
     end
     %更新当前最好解的距离值
     BLHistory(iter,1) = Bdist;
     if showProg
         figure(2);
         for i = 1:(N-1)
             plot([xy(Broute(i),1),xy(Broute(i+1),1)],[xy(Broute(i),2),xy(Broute(i+1),2)],'bo-');%画出路线图
             hold on;
         end
          plot([xy(Broute(N),1),xy(Broute(1),1)],[xy(Broute(N),2),xy(Broute(1),2)],'ro-');%画出终点到起点的线
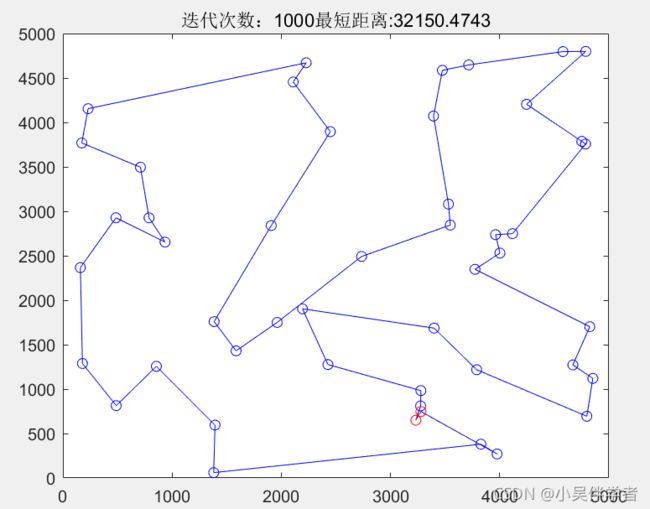
          title(['迭代次数：', num2str(iter),'最短距离:',num2str(Bdist)]);
          hold off;
     end
end
if showResult
    Bestroute = Broute;
    MinLength = Bdist;
    figure(3);
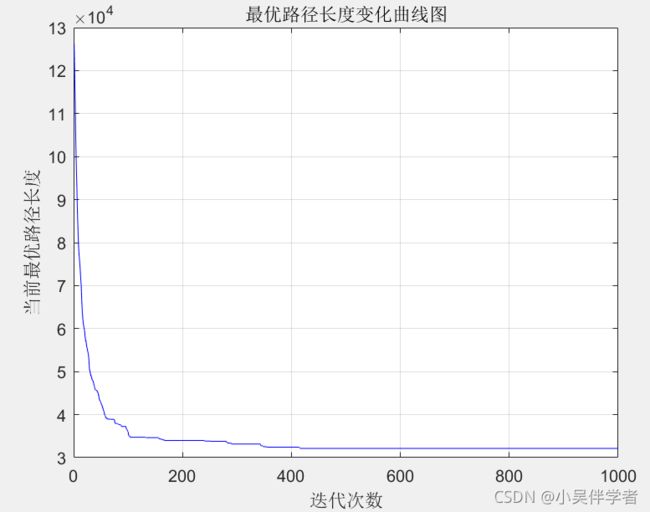
    plot(BLHistory,'b');%画出最优路径长度与迭代次数的关系
    xlabel('迭代次数');
    ylabel('当前最优路径长度');
    title('最优路径长度变化曲线图');
    grid;
    hold on;  
end
if nargout%如果需要输出结果
    TspTBout{1} = Bestroute;
    TspTBout{2} = MinLength;
end

function L = CalDistofS(dmat,S)
     dist = 0;
     n = size(S,2);
     for k = 1:(n-1)
         dist = dist +dmat(S(k),S(k+1));%中间路径的距离
     end
     L = dist + dmat(S(n),S(1));%回到起点的距离
end

end

 

由于代码有较多的注释，就不在解释太多了，直接上结果图吧！

若有小伙伴对机器人任务分配算法较为兴趣的，可以在下面评论交流一波，纯属互相学习!