分组交换
1、什么是分组交换?
电路交换
电路交换最早用于电话网络,两台电话之间用专有电线连接,一台电话只能和连在电线上的另一台电话通信。

但实际上,为了能和其他人通信,专有电线会连接到交换中心。在交换中心,操作员会手工将输入的专有电线连接到待连接的电话的专有电线上。这里的重点是电线从通话开始到结束都是专有的。

今天使用的电路交换网都是自动切换的。

容易想到,打一个电话要经过三个阶段。首先,我们拿起听筒并拨号,拨打的号码说明了我们要连接的地方。这样就形成了从一端到另一端到专有电路,这样一来,专有电路将遍历所有电路,系统告知了每段电路将输入线连接到输出线。每个电路交换机都要维持状态以将输入电路映射到正确的输出电路上。
第二阶段,在大多数像电话一样的数字电话系统中,我们的声音在第一个交换机处被采样和数字化。然后,通过专有电路将其作为64Kb信道的语音发送。因此,我们的电话通信在整个通信过程中都有专用的电路或信道,电路不与其他人共享。
最后,当我们挂断电话后,电路必须被移除,并且沿着路径上的交换机的状态也必须被移除。

实际上,在交换机间存在中继线,它们非常非常快,即很高的比特率。即使是最慢的也有2.5Gb/s,最快的有40甚至100Gb/s。如图所示,这个干线看起来很大,实际上它比头发还细,所有的电话呼叫都使用这条干线。但每个电话呼叫都有专用的64Kb/s的电路,不与他人共享。

总结
- 每个电话呼叫都有自己的私有、有保证的、端到端的独立数据传输速率
- 一次电话呼叫有三个阶段:
- 建立端到端的电路(拨号)
- 通话
- 关闭电路(拆卸)
- 最初,电路是端到端的物理电线
- 如今,电路就像一根虚拟的私人电线,实际使用的电线会与其他人共享,但在电线内部有自己的专用电路
问题
- 效率低下。计算机通信往往是非常突发的。例如,通过ssh连接键入,或查看一系列网页。如果每个通信都有一个专用电路,它的使用效率将非常低。
- 不同的速率。计算机以许多不同的速率通信。例如,一个6Mb/s的流媒体视频服务器,或者我以每秒1个字符的速度打字。固定速率的电路用处不大。
- 状态管理。电路交换需要维护每一个通信的必须管理的状态。
分组交换

在分组交换中没有专用的电路来传输数据。相反,我们可以通过添加一个标头,在数据准备好的任何时候发送一块数据,它就是分组或数据包(packet)。标头里包含了数据包的目标地址。

分组交换网络由终端、链路和分组交换机组成。

当我们发送数据包时,它从源被逐跳地路由到目的地。

沿途的每次分组交换都要在交换机的转发表中查找下一跳的地址。
在互联网中,存在许多不同类型的分组交换机。其中一些称为路由器,因为它们处理的是因特网地址,并且其中的还包含我们办公桌上的小型路由器或大型配线间的大型路由器。还有一些称为以太网交换机。

分组交换机还有缓冲区。

如果两个包同时到达,交换机必须安置其中一个,因为无法同时发送它们,它只能一次发送一个。

缓冲区保留数据包:
- 当两个或以上的数据包同时到达
- 在拥塞期间
总结
- 数据包通过在路由器本地的转发表中查找地址来独立路由
- 所有数据包共享链路的全部容量
- 路由器不维护每个通信的状态
为什么互联网使用分组交换
有效利用昂贵的链路
- 链路被认为是昂贵和稀缺的
- 分组交换允许很多突发流有效地共享同一链路
- “电路交换很少用于数据网,…因为网络的使用效率很低” —— Bertsekas/Gallager
对链路和路由器的故障具有弹性
- “为了高可靠性,…互联网将成为数据报子网,因此,如果某些线路或路由器被破坏,则信息很容易被重新路由。“ —— Tanenbaum
互联网最初被设计为现有网络的互连。那时,几乎所有广泛使用的通信网络使用的是分组交换,所以互联网也需要设计为分组交换网。
2、端到端时延
传播时延
包装时延(传输时延)

注意:示例2中,1kbit为1024bit,1kb/s为1000bit/s
端到端时延

当来自不同链路上的数据包同时进入一个交换机并都想从同一条链路出去时,某些数据包必须在路由器的队列中等待。队列也被称为数据包缓冲区。通常,队列是先进先服务的。数据包缓冲区可以防止数据包被丢弃,每个交换机都有自己的数据包缓冲区,它们是分组交换的基础。如果没有数据包缓冲区,每当两个数据包同时出现时,我们都不得不丢弃其中一个。
但是数据包缓冲区改变了端到端时延的表达式。如果我们的数据包到了,队列里还有一些数据包,它将延迟转发到下一条链路的时间,因为它不得不等待它前面的数据包先离开。

这里要注意的是,除了排队时延,其它时延都是确定的。
下面是从斯坦福大学ping普林斯顿大学和清华大学的累计分布关于RTT的函数图。

斯坦福大学距离普林斯顿大学约4000公里,距离清华大学约10000公里,因此对于前者,传播时延更低。同时可以注意到图中圈住的部分,到普林斯顿的RTT区间范围比到清华大学要小,前者大约为100-200,后者约为320-500。这是因为随着通信距离变长,途中的排队时延也增加的缘故。排队时延可能占了整个端到端时延的一半。
总结
端到端时延由三个主要部分组成:
- 沿链路的传播时延(固定)
- 将数据包放到链路上的包装时延(固定)
- 路由器数据包缓冲区中的排队时延(不定)
3、播放缓冲区
问题描述
有一些应用程序必须关心排队时延,特别是例如流视频和语音等实时应用程序。基本上,因为这些应用程序无法确切地知道数据包何时出现,所以它们不能确定能否及时提供语音或视频样本给用户。因此,它们在所谓的播放缓冲区中积累了很多数据包。通过预先积累数据包,可以防止某些数据包没有及时到达而影响体验的情况。

在设计播放缓冲区的时候,必须考虑缓冲区能走多远。

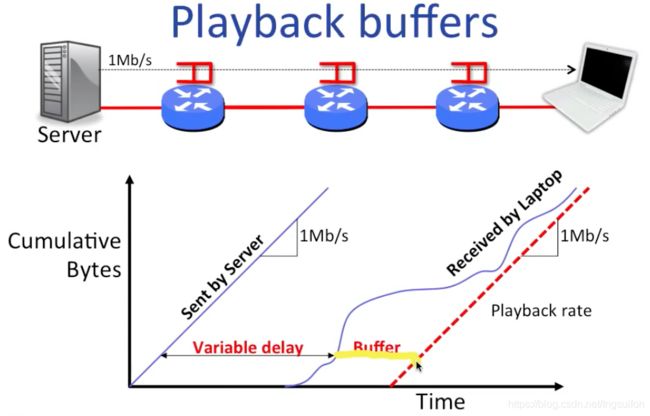
假设我们使用下图中右边的笔记本观看来自左边服务器上的视频。为了方便,服务器的传输速率(单位时间内被送到链路上的比特数)为1Mb/s,路径上只有3个路由器。下面的函数图中,自变量为时间,因变量为累计的字节数。左边的函数为服务器随时间发送的字节数,因为传输速率恒定,所以显然是线性函数。右边的曲线为笔记本累计接收到的字节数,由于排队时延的不定性,因此函数呈无规则曲线状。
两曲线间的水平距离表示每个特定的字节从它被发送到它被接收的总时延。由于排队时延的不定性,因此总时延也是不定的。两曲线间的竖直距离表示还在传输路径上的字节数。
从图中我们还可以获取很多有用的信息。首先,端到端的总时延不能小于分组时延和传播时延,因此两曲线间的水平距离有一个下限。然后,它还有一个上限。因为每个路由器的缓冲区都是有限大小的,所以可以假设一个数据包经过每一个路由器时都排了最长的队,将这些最大值添加到总时延中就得到了上限。但是上限没什么用,因为它通常非常非常大。最后,对于右边的接收曲线,它每一点的斜率都为正且不应超过最后一个路由器到笔记本之间的链路的数据率。

最右边的直线表示随时间播放的字节数。中间的黄线表示的是一个特定字节从开始发送到开始播放之间的时延。

下图的水平黄线表示的是一个特定字节已缓冲的时间。
同理,竖直黄线表示的是当前缓冲区中的使用量。从图中可以看出,一开始缓冲区里的字节一直在积累,然后随着视频开始播放,积累的字节数开始减少,缓冲区甚至差点空了,幸运的是缓冲区里的字节数又开始增多了,最终一切顺利。

粗略地看一下客户端的内部,playback point指向的是已到达的位置,它就是视频播放器中进度条上的点。从播放缓冲区中取出字节后,将它们交给视频解码器,最终在屏幕上播放。

下面看一个糟糕的情况。如果我们在播放第一个字节前没有等待足够长的时间,就会导致缓冲区生产的速度低于消费的速度,缓冲区变空,意味着我们没有要解码并在屏幕上播放的字节。


客户端要怎么做呢?它必须让缓冲区更大一些,并重新缓存。为了做到这一点,屏幕会被“冻结”,等待一些字节积累,然后它才能继续播放。

总结
- 在分组交换中,端到端的延迟是可变的
- 我们使用播放缓冲区来吸收这种变化
- 我们可以把播放缓冲区设得很大,但是这也会导致我们等待缓冲区被填充的时间变长,也就是我们不得不延迟我们开始观看视频的时间
- 因此,应用程序会估计延迟,设置延迟缓冲区,并在延迟改变时调整缓冲区大小。
4、队列模型
简单的确定性队列模型

A(t):到时间t为止累计到达的字节数
Q(t):t时刻队列中的字节数
D(t):到时间t为止累计离开的字节数
如图,这就像一个水桶,上面有水流入,下面有水流出,中间的部分就是累计量,即队列。

上图使用的是存储转发模型。

看一个例子:

上图中的平均值计算可以用积分,结果是一样的。
小型数据包减少了端到端的延迟

上图右边的表达式的第二项严格来讲应该为 ( M P − 1 ) ∗ r 3 (\frac{M}{P}-1)*r_3 (PM−1)∗r3,因为第1个数据包已经计算在第一项中了,不过这里不影响理解。从左图中可以看出,如果整个报文以一个数据包发出,在开始第2段链路传输时,必须等待所有比特到达;而如果分成更小的数据包,那么每个数据包都是独立传输,不必等待其它数据包,这样就形成了流水线的效果,增强了并行性,减少了端到端延迟。
统计复用
如图,如果所有链路都以全速率R运行,那么输出链路将不堪重负,并且很快开始丢弃数据包。实际上,将有NR的速率输入,而只有R的输出速率。但由于统计复用和到达的突发性,如果平均速率较低,我们有可能避免这种情况。

下面有两条不同的链路输入同一个路由器,其中一个的比特率为A,另一个为B,输出链路的比特率为C。从图中可以看出,两峰重叠的时刻是很少的。

将两者的速率相加,因为峰值没有重叠,所以加起来的和小于两曲线的最值和。注意这里我们没利用缓冲区的存在这一条件。

下图考虑R‘,这时,输出顶不住输入的压力,会讲多的部分放入缓冲区中。

总结
- 通常,我们可以使用简单的确定性队列模型来理解网络中的包动态
- 我们将消息分成数据包,因为它允许我们通过流水线传输消息,并减少端到端的延迟
- 统计复用使我们能够在一个链路上高效地传输多个流
5、有用的队列特性
通常情况下,到达过程是复杂的,所以我们通常使用随机过程来建模。
研究具有随机到达过程的队列称为排队论
具有随机到达过程的队列有一些有趣的特性。
队列随时间的变化

蓝色箭头表示一个数据包到达,红色箭头表示离开,队列的占用情况由最下方的Q(t)和数字表示。图中的虚线红箭头表示队列为空时不能发送数据包。
队列属性1:突发性到达会增加延迟

假设这是一个均匀到达的数据包序列,如图,每1秒到达一个数据包,在这种情况下,队列占用为0或1,即小于等于1,平均占用情况介于0和1。

和刚刚类似,到达链路和输出链路的数据率都不变,不过这一次是每N秒会有来自N个不同链路上的N个数据包同时到达(突发性),队列的占用情况Q(t)如图所示。可以看到,范围变大了,为0-5,并且整个过程一直在变化,均值和方差都变大了。
总的来说,突发性到达会增加延迟,虽然这个简单的例子不能真正证明这一点,但我们也可以从直观上了解到它。
队列属性2:确定性使延迟最小化
这和第1个属性是刚好平衡的。随机到达的平均等待时间比简单的周期性到达要长。
队列属性3:Little’s Result

λ为平均到达速率,L为平均队列长度,d为平均排队延迟。上面看似简单的结论适用于任何没有客户丢失或被丢弃的队列。
泊松过程
- 新到达电话交换机的电话呼叫
- 许多独立核粒子的衰变
- 电路中的散粒噪声
它使数学变得容易
警示
- 网络流量非常具有突发性
- 数据包到达不是泊松分布的
- 但它很好地模拟了新流量的到来
M/M/1队列

第1个M:Markovian arrival process(马尔可夫到达过程),在这里是泊松过程
第2个M:Markovian service process(马尔可夫服务过程),在这里是指数过程
1:1个服务者,即图中为队列服务的输出链路
这个模型很简单,但也经常用来模拟各种复杂的排队系统。
平均排队延迟: d = 1 μ − λ d=\frac{1}{μ-λ} d=μ−λ1
可以看出,随着负载的增加,即 λ u \frac{λ}{u} uλ越趋近于1,平均延迟会越来越大
由Little’s Result, L = λ d L=λd L=λd,所以 L = λ u − λ = λ u 1 − λ u L=\frac{λ}{u-λ}=\frac{\frac{λ}{u}}{1-\frac{λ}{u}} L=u−λλ=1−uλuλ,当λ逐渐增加越趋近于u,队列就越来越长,延迟就越来越大。
因此,尽管M/M/1永远不可能是实际排队系统的队列占用率或平均延迟的性能度量,但它仍为我们提供了很好的直观感受。
总结
队列特性
- 突发性到达会使延迟增加
- Little’s Result: L = λ d L=λd L=λd
数据包的到达不是泊松的,但一些事件是,例如web请求和和一些新流量到达
M/M/1队列是一个简单的队列模型
6、分组交换机的工作方式(1)
通用分组交换机

一个数据包到达后,先通过转发表查询目的地址对应的输出链路,然后可能要更新数据包的头信息(例如,对于互联网路由器,TTL要减1,然后重新计算校验和),接下来可能要在缓冲区中排队,轮到它后才被发送到输出链路。
下面看看多个数据包的情况。

如图,红色的数据包会选择从红色圆点出去,蓝色数据包会从蓝色圆点出去,圆点表示链路。

如图,蓝色数据包被送出,红色数据包的一个被送出,另一个进入缓冲区排队。

一旦前面的数据包离开了,它就可以继续向前传输了。
以太网交换机
- 检查每个到达帧的报头
- 如果以太网目标地址在转发表中,则转发帧到正确的输出端口
- 如果以太网目标地址不在表中,则广播帧到所有端口(帧到达的端口除外)
- 表中的条目是通过检查到达包的以太网源地址
互联网路由器
- 如果到达帧的以太网目的地址(MAC地址)属于路由器,接受帧;否则丢弃
- 检查数据报的IP版本号和长度
- 减少TTL,更新IP报头校验和
- 检查TTL是否为0
- 如果IP目的地址在转发表中,则转发到下一跳的输出端口
- 找到下一跳路由器的以太网目的地址(ARP协议)
- 创建一个新的以太网帧并发送它
基本操作
- 查找地址:在转发表中如何查找地址?
- 交换:如何将数据包发送到正确的输出端口?
查找地址:以太网
查找地址:IP
最长前缀匹配的实现1:Trie树

这有点像哈夫曼树,0往左走,1往右走,可以到达唯一的叶节点。如果我们到达一个叶子结点发现那里为空,则回退到最近的匹配点
最长前缀匹配的实现2:TCAM

连续X前面的位表示需要匹配的前缀,X表示表示无需匹配。掩码用来说明这一点。用这个实现的匹配是暴力匹配,即和表中的每一项都要去匹配。
查找地址:通用
总结
分组交换机执行两种基本操作:
- 在转发表中查找地址
- 切换到正确的输出端口
在高层次上,以太网交换机和因特网路由器执行类似的操作
地址查找在交换机和路由器中表现得非常不同
7、分组交换机的工作方式(2)
输出队列的分组交换
如图,在每个输出链路上都有缓冲区,当发生拥塞时数据包被缓存在此。



当前面的数据包离开后它才能离开。(FIFO)

考虑非常糟糕的情况,所有链路上同时到达的数据包都想从同一条链路输出。

假设所有链路的数据率均为R,则对于队列来说,输入速率为NR,输出速率为R,对于这块内存来说,它的总运行速率就要为(N+1)R。当N可能非常非常大时,建立可伸缩的队列内存是极为困难的。我们期望的总速率应该是2R,即输入R,输出R。
输入队列的分组交换
解决上述问题的一种方法是将队列移动到输入中。

和刚刚一样的例子:

另一个红色数据包被缓存:
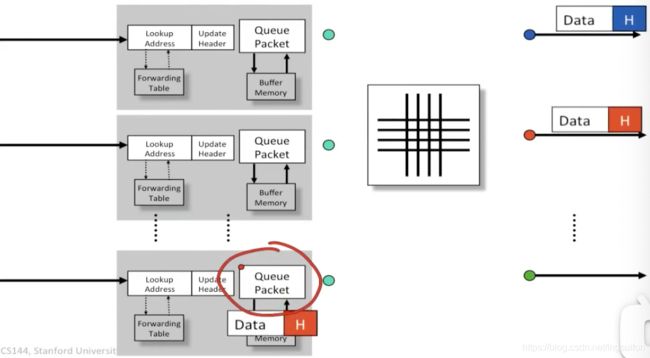
当前面的包离开后,它才能继续:

这里的好处在于,同一时间队列中只会有一个数据包(不可能有多个数据包同时从一条链路上到达),这样一来输入的速率为R,输出速率为R,那么总速率就从(N+1)R减少为了我们期望的2R。
但这个办法同样有问题。
队头阻塞
如图为所有链路的输入队列情况,此时所有队列的队头数据包都想要从红色链路输出。
1.

2.

3.

尽管队列中有要发送到其它链路的数据包,但由于队头元素的阻塞,导致这一轮发不出去。
虚拟输出队列
解决队头阻塞的一个办法是使用虚拟输出队列,其中每个输入为每个输出维护一个单独的队列。

如图,三个输入,三个输出,因此在每个输入中有三个队列。

如图,对每个输入中的数据包,根据要输出的链路分别安排在对应的队列中。

这样一来,就不会发生队头阻塞了。

虚拟输出队列实际上在生活中很常见,如图,左转车道的车在对面有车过来时不能通行,即被阻塞,而右边的直行车道和右转车道上的车都不受影响。

总结
分组交换机执行两种基本操作:
- 在转发表中查找地址
- 切换到正确的输出端口
最简单和最慢的交换机使用输出队列,这将使数据包延迟最小化
高性能交换机通常使用输入队列,通过虚拟输出队列来最大化吞吐量






