2023.05.21 学习周报

---

摘要

This week, I read a computer science related to time series prediction. At present, the severity of PM2.5 has affected public health, economic and social development. However, due to the strong nonlinearity and instability of air quality, the volatile change of PM2.5 over time is difficult to predict. In view of the above problems, VMD and BiLSTM were combined to build a mixed deep learning model VMDBiLSTM, which was used to predict the changes of PM2.5 in urban air in China. The original PM2.5 sequence data was decomposed into multiple sub-signal components according to frequency domain by VMD, and then BiLSTM was used to predict each sub-signal component respectively. The experimental results show that the proposed models are superior to the compared models and significantly improve the prediction results. In addition, I learn TOPSIS and finite element method: 1) The key steps of TOPSIS method are sorted out, and then the algorithm is implemented by python. 2) Through a simple heat transfer model of a cylinder, the analytical solution is learned, and the concrete implementation of the finite element method is learned.

本周，我阅读了一篇与时间序列预测相关的文章。目前，PM2.5的严重程度已经影响到公众健康、经济和社会发展等方面。但由于空气质量具有较强的非线性和不稳定性，PM2.5随时间的挥发性变化难以预测。针对以上问题，将VMD和BiLSTM相结合，构建混合深度学习模型VMDBiLSTM，用于预测中国城市空气中PM2.5的变化。通过VMD将原始PM2.5序列数据按频域分解为多个子信号分量，然后再利用BiLSTM分别对各子信号分量进行预测。实验结果表明，提出的模型均优于相比较的模型，并且显著提高了预测结果。此外，我学习了优劣解距离法和有限元法：1）通过对TOPSIS法的关键步骤进行梳理，然后用python对算法完成了实现；2）通过一个圆柱体的简单传热模型，学习了解析求解，以及对有限元法的具体实现进行了学习。

---

文献阅读

1.题目

文献链接：A hybrid deep learning technology for PM2.5 air quality forecasting

2.背景

由于全球城市化进程的加速，全球空气质量普遍显著下降。在许多国家，空气污染事件或异常天气显著增加，这种污染严重威胁着当地的生活和社会发展。因此，近年来，在快速发展的人工智能技术中，加强对空气质量的监测和对空气污染的预测已经成为越来越热门的话题。

3.现存问题和解决方法

现存问题：数值模拟方法通过数值计算建立基于物理和化学性质的模型，通过分析PM2.5在大气中的分布并求解守恒方程进行预测。它通常更实用，可以提供系统的预测结果。然而，它需要关于区域气候、山地地貌和污染源分布的详细和精确的信息。

解决方法：对此，文章采用前沿的双向长短期记忆神经网络去预测PM2.5的时间序列数据。其中主要用到LSTM和VMD两种技术，LSTM以其独特的门控结构，通过控制信息的选择性处理来防止梯度消失和梯度爆炸，从而避免了长期依赖问题；VMD对PM2.5非周期信号进行频域分解，通过将复杂信号分解成多个谐波子序列来降低输入信号频域复杂度。

4.方法

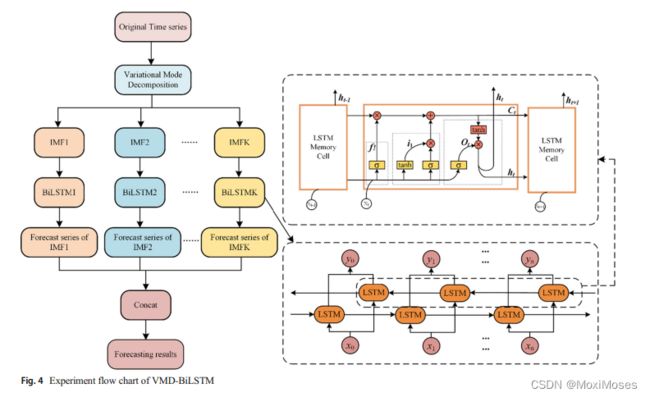
4.1 Variational mode decomposition (VMD)

1）构造一个变分问题，将PM2.5数据分解为K个模态变量，每个模态uk(t)是一个有限带宽，中心频率ωk。变分问题的目标函数是各模态估计带宽的最小和，约束条件是各模态分量的和等于原信号（δ(t)是狄拉克函数，f是原始信号，*是卷积算子）。表达式如下：

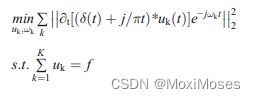
2）为了得到约束变分问题的最优解，引入惩罚因子α和拉格朗日乘法算子λ(t)，将约束变分问题转化为无约束变分问题。表达式如下：

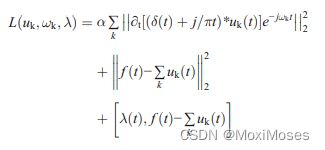
3）采用ADMM迭代算法对得到的模态分量和中心频率进行优化，求解增广拉格朗日方程迭代器的最优解。迭代过程如下：

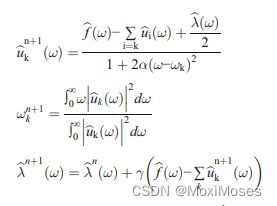
4）下图为VMD分解后的PM2.5原始时间序列数据波形，波形由低频向高频分布：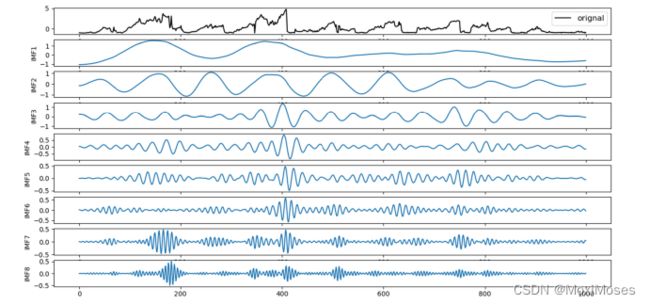

4.2 Bidirectional LSTM

BiLSTM的内部单元结构：

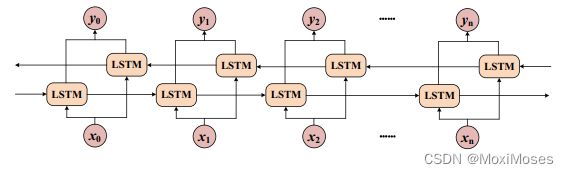
从图中可以看出，BiLSTM模型由前向LSTM和后向LSTM组成，这使得模型可以获得当前时间的正向和后向特征。与LSTM相比，BiLSTM的输出更能体现受到了前后数据的影响。

5.实验

5.1 数据标准化

数据集：UCI机器学习知识库，是美国大使馆2013 - 2017年记录的北京周边12个观测站的空气质量数据。采用zero-mean standardization对数据进行处理，得到均值为0，标准差为1，服从标准正态分布的数据标准化。标准化和去标准化公式为：

5.2 评价指标

实验中使用了五个评价指标，平均绝对误差(MAE)、均方根误差(RMSE)、平均绝对百分比误差(MAPE)、决定系数(R2)和预测趋势精度(ACC)。计算公式如下：

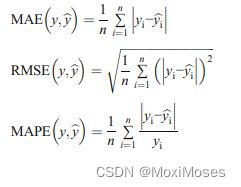
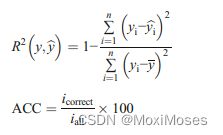
5.3 实验过程及结果

1）首先确定K的值，它决定了对原始时间序列数据进行IMF分解的次数。

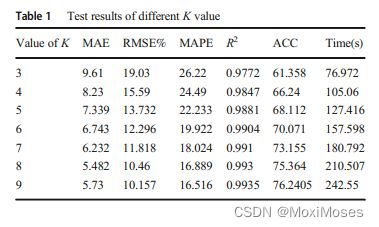
2）从图中可以看出，IMF8曲线波动剧烈，且幅度较大。这种波动导致预测结果不理想，这也是影响预测效果的主要因素之一。

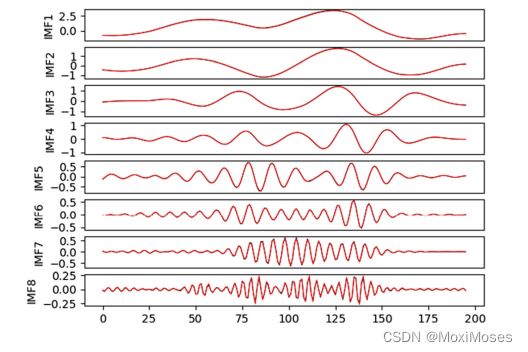
3）为了进一步证明该模型的有效性，使用了几个已有的时间序列预测模型进行比较。

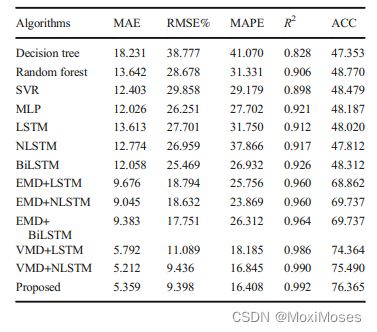
4）下图结果表明，所提出的VMD-BiLSTM预测方法具有预测误差小、与实际数据拟合度高、趋势预测精度高、模型稳定性好、泛化能力强等优点。

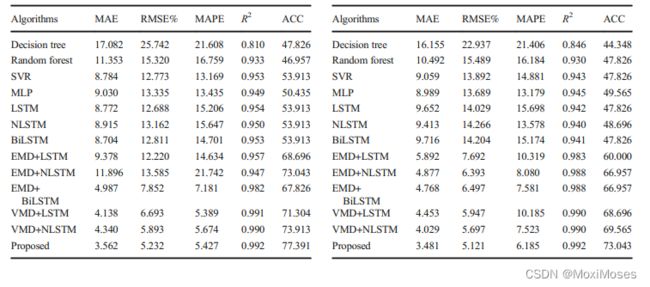
6.结论和展望

结论：
1）针对PM2.5浓度数据的非线性、非周期性和非平稳的复杂性特点，提出了一种混合神经网络VMD-BiLSTM模型进行精确的时间序列预测。
2）采用最前沿的数据分解方法VMD，将PM2.5原始时间序列数据按频率分解为一组IMF序列。
3）利用BiLSTM神经网络构建IMF各分量的训练和预测模型，然后将预测子序列的结果进行组合，得到最终的预测结果。
4）实验证明了VMD-BiLSTM模型在预测误差和趋势预测精度方面，均优于其他时间序列预测模型。
5）实验证明与EMD分解相比，VMD有效地避免了预测的延迟现象。

展望：
1）将模型扩展到其他预测领域（具有很强的非线性和非平稳性），如光伏预测和家庭用电预测。
2）将综合考虑空气质量数据序列的波动性，进一步研究多通道空气质量预测模型。

优劣解距离法

python代码实现：

import pandas as pd
import numpy as np


# 1.极小型指标转化为极大型指标
def dataDirection_1(datas, offset=0):
    def normalization(data):
        return 1 / (data + offset)

    return list(map(normalization, datas))


# 2.中间型指标转化为极大型指标
def dataDirection_2(datas, x_min, x_max):
    def normalization(data):
        if data <= x_min or data >= x_max:
            return 0
        elif x_min < data < (x_min + x_max) / 2:
            return 2 * (data - x_min) / (x_max - x_min)
        elif x_max > data >= (x_min + x_max) / 2:
            return 2 * (x_max - data) / (x_max - x_min)

    return list(map(normalization, datas))


# 3.区间型指标转化为极大型指标
def dataDirection_3(datas, x_min, x_max, x_minimum, x_maximum):
    def normalization(data):
        if x_min <= data <= x_max:
            return 1
        elif data <= x_minimum or data >= x_maximum:
            return 0
        elif x_max < data < x_maximum:
            return 1 - (data - x_max) / (x_maximum - x_max)
        elif x_min > data > x_minimum:
            return 1 - (x_min - data) / (x_min - x_minimum)

    return list(map(normalization, datas))


# 4.计算各指标的熵值, 合理确定指标权重
def entropyWeight(data):
    data = np.array(data)

    # 归一化
    P = data / data.sum(axis=0)

    # 计算熵值
    E = np.nansum(-P * np.log(P) / np.log(len(data)), axis=0)

    # 计算权系数
    return (1 - E) / (1 - E).sum()


# 5.计算得到评价结果
def topsis(data, weight=None):

    # 归一化
    data = data / np.sqrt((data ** 2).sum())

    # 最优最劣方案
    Z = pd.DataFrame([data.min(), data.max()], index=['负理想解', '正理想解'])

    # 距离
    weight = entropyWeight(data) if weight is None else np.array(weight)

    Result = data.copy()
    Result['正理想解'] = np.sqrt(((data - Z.loc['正理想解']) ** 2 * weight).sum(axis=1))
    Result['负理想解'] = np.sqrt(((data - Z.loc['负理想解']) ** 2 * weight).sum(axis=1))

    # 综合得分指数
    Result['综合得分指数'] = Result['负理想解'] / (Result['负理想解'] + Result['正理想解'])
    Result['排序'] = Result.rank(ascending=False)['综合得分指数']

    return Result, Z, weight


root = "../data"
city = "桂林市"
station = "八中"
excel = f"{root}/{city}/{station}.xlsx"

if __name__ == '__main__':
    data = pd.DataFrame(pd.read_excel(excel, index_col=0).drop(["城市", "站点名称"], axis=1))
    # print(data)
    data['SO2'] = dataDirection_1(data['SO2'])
    data['PM2.5'] = dataDirection_1(data['PM2.5'])
    data['PM10'] = dataDirection_1(data['PM10'])
    data['NO2'] = dataDirection_1(data['NO2'])
    data['O3'] = dataDirection_1(data['O3'])
    data['CO'] = dataDirection_1(data['CO'])
    [Result, z1, weight] = topsis(data)
    print(Result)
    print(z1)
    print(weight)
    Result.to_excel('../data/八中分析数据.xlsx', sheet_name='分析结果')

TOPSIS法的关键点：
1）指标属性同向化：一般选择指标正向化，TOPSIS 法使用距离尺度来度量样本差距，因此需要对指标属性进行同向化处理。其中：若一个维度的数据越大越好，另一个维度的数据越小越好，这会造成尺度混乱。
2）构造归一化初始矩阵：构造加权规范矩阵，属性进行向量规范化，即每一列元素都除以当前列向量的范数（使用余弦距离度量）。
3）确定最优方案和最劣方案，计算各评价对象与最优方案、最劣方案的接近程度。
4）确定指标的权重：这里采用了熵值法，熵值越大，表明指标值提供的信息量越多，则该指标的权重也应越大。

有限元

1.求解一个简单的传热问题

下图是我们要研究的一个简单对象，实际上它只是一根很长的发热圆柱体的一部分，浸入水中：

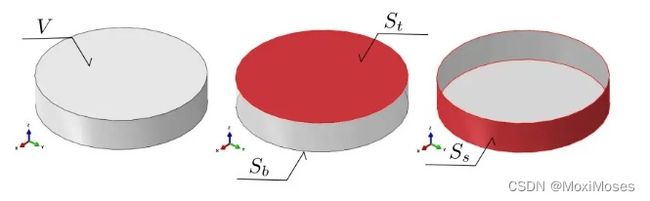
1）边界条件
由于圆柱体只是一根棒的一部分，上下表面的温度不应该存在温度梯度（第二类隔热边界条件）：
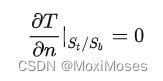无限长的棒在轴向没有热量的流动，此外人为给定一个边界处的温度值：

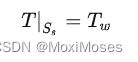
2）解析求解公式

2.有限元如何实现

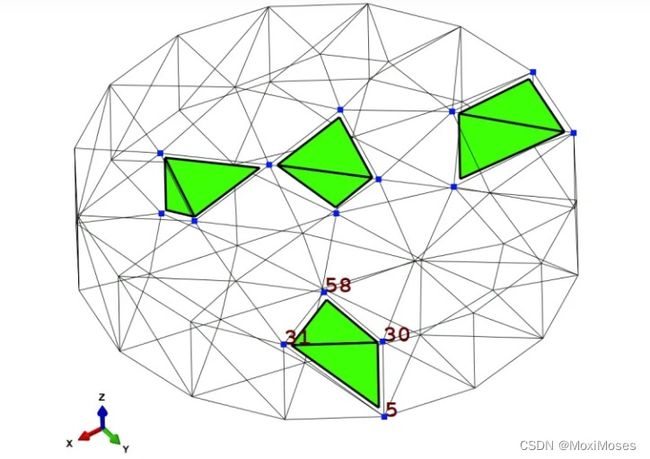
有限元法依托于网格或网格单元，如上图所示，绿色四面体就是这样的单元，蓝色点称作节点。假设温度在单元内线性分布，当单元足够小时，在某个单元内的温度场：

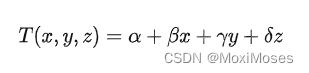
假设温度呈线性分布和单元是三维实体，所以给定三维坐标，就可以根据上面的表达式给出温度。对于不同单元，就存在不同的四个系数，而且对于不同单元的系数之间是不独立的，因为温度在整个实体域中是连续的，所以当两个单元相连时（如：顶点、边、面相接触），需要使得在相连区域温度值相同。

四个系数只需要四个方程就可以求出来，即代入四个已知点的温度。因此，只需要求得四面体单元的四个节点处的值，就可以求出四个系数，就可以求出单元内任意点的值了。

因此，有限元法就是只需要计算出有限数量的值，其他的值就可以通过这些值插值求得：

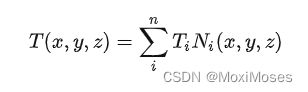
其中：Ti 是单元四个节点处的温度值，Ni(x, y, z)是基函数，可以看作一个权重。

---

总结

本周，我学习了优劣解距离法，它能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距。而且该方法对数据分布及样本含量没有严格限制，数据计算简单易行。此外，我学习了有限元法，了解到有限元法是如何实现，以及对其的基本思想有了一定的认识。下周，我将继续学习有限元法的相关知识。